基于混合樽海鞘-差分进化算法的贝叶斯网络结构学习算法

刘彬，范瑞星，刘浩然，张力悦，王海羽，张春兰

（1. 燕山大学信息科学与工程学院，河北 秦皇岛 066004；2. 河北省特种光纤与光纤传感重点实验室，河北 秦皇岛 066004）

1 引言

贝叶斯网络（BN, Bayesian network）是结合图论和概率论来表示因果知识的概率图模型，是用于不确定领域中推理和预测的最佳方式之一[1]。贝叶斯网络可以用图论的语言直观地揭示问题的结构，并利用该结构降低概率推理的计算复杂度。由于贝叶斯网络直观易懂，在风险分析、机器学习、信息学等研究领域[2-3]都有应用。

贝叶斯网络的构建包含结构学习、参数学习和推理学习。结构学习是基础与核心，完备数据下的结构学习方法主要有3种：基于依赖性测试的方法[4]、基于评分搜索的方法[5]和混合方法[6]，其中常见的结构学习方法是基于评分搜索的方法，即在所有节点的结构空间内按照一定的搜索策略及评分准则构建贝叶斯网络结构。

基于评分搜索的方法学习贝叶斯网络结构是一种 NP问题[7]，国内外学者通常利用启发式算法来解决此类问题。Tsamardinos等[8]提出了一种基于依赖性测试和爬山算法的最大最小爬山（MMHC,max-min hill-climbing）算法，该算法虽然改善了检索策略，降低了搜索空间复杂度，但由于搜索空间的缩小易导致算法陷入局部最优。刘浩然等[9]提出了基于最大支撑树（MWST, most weight supported tree）和蚁群算法（ACO, ant colony optimization）的混合搜索节点序算法（MAK, MWST-ACO-K2），该算法在处理小型网络时可取得较理想的结果，但是与其他基于节点序搜索算法类似，需要对种群中所有个体运行K2算法得到对应的适应度值，在大网络中存在时间复杂度较高、结果较差等问题。Wang等[1]提出了基于离散水循环算法的贝叶斯结构学习算法（BEWCA-BN, binary encoding water cycle algorithm for BN structures learning），该算法根据逻辑算子提出了改进的水循环算法更新个体，其中蒸发策略虽然提高了算法跳出局部最优的能力，但在小网络中通常需要花费更多的时间寻找最优解。Contaldi等[10]提出了基于精英遗传算法的贝叶斯结构学习算法（AESL-GA, adaptive elite-based structure learner using genetic algorithm），该算法采用自适应的控制参数来避免参数设置对结果的影响，在小网络中学习到了较优的网络结构，但在大网络中由于缩小搜索空间导致学习到的结果不太理想。

上述启发式算法应用于贝叶斯网络结构学习时由于参数设置对搜索过程的影响，存在搜索效率较低、易陷入局部最优等问题，而Seyedall等[11]提出的樽海鞘算法（SSA, salp swarm algorithm）具有参数较少、操作简单、易于实现等优点。SSA将种群划分为引领者（leader）与跟随者（follower），通过引领者领导跟随者形成 slaps链进行种群寻优。在处理复杂问题时由于引领者对跟随者的引领作用，容易使整个种群过早地聚集于局部最优解[12]。

本文将SSA应用到贝叶斯网络结构学习，同时为了避免SSA陷入局部最优，将全局寻优能力强的差分进化（DE, differential evolution）算法[13]与SSA融合，构建了一种混合樽海鞘-差分进化（HBSS-DE,hybrid binary salp swarm-differential evolution）算法。该算法首先设置规模因子将种群划分[14]为较好种群和较差种群。然后构建樽海鞘搜索策略更新较好种群，提高算法的收敛速度；构建差分搜索策略更新较差种群，避免陷入局部最优，并在合并子种群时利用变异算子增大搜索范围。最后通过种群的迭代搜索最佳结构。

2 HBSS-DE算法的构建

HBSS-DE算法利用最大支撑树与爬山算法建立初始种群P0，然后将P0降序排列更新为种群P，并设置规模因子将种群P划分为较好种群P1与较差种群P2。构建樽海鞘搜索策略更新P1，建立差分搜索策略更新P2。合并为种群P时利用两点变异算子增加种群的多样性，并根据规模因子重新划分P进入下次迭代。迭代结束输出种群P中评分最高的樽海鞘个体，即最佳的贝叶斯结构。

2.1 初始种群的建立及划分

根据数据样本计算目标网络各节点间的互信息，利用2个节点间的互信息可以得出这2个节点是否相关[15]，不存在相关关系的节点必然不存在因果关系。以变量X、Y为例，互信息I(X,Y)为

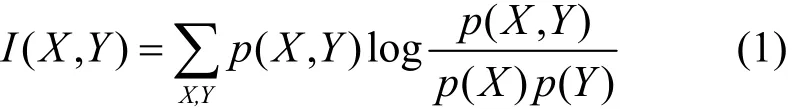
其中，p(X,Y)为变量X和变量Y的联合概率，p(X)为变量X的概率，p(Y)为变量Y的概率。

根据互信息计算各节点之间的权重，利用最大支撑树原则生成一个候补结构[16]，可以有效地缩小搜索的空间。该候补结构中，除树形结构之外的节点利用爬山算法中的加边、减边、转边算子得到樽海鞘种群。其中每个樽海鞘代表的贝叶斯网络结构可用如图1所示的邻接矩阵表示。

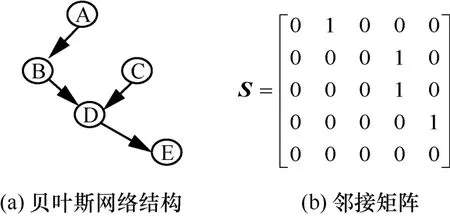
图1 樽海鞘个体

采用贝叶斯信息准则（BIC, Bayesian information criterion）评分函数对樽海鞘个体评价。根据BIC评分函数的可分解性，当BN中的局部结构改变时，为了减少重复计算的次数，只需利用式(2)计算改变的局部结构G1的评分fnew(G1,D)，然后代入式(3)即可得到樽海鞘个体的评分f(G,D)。

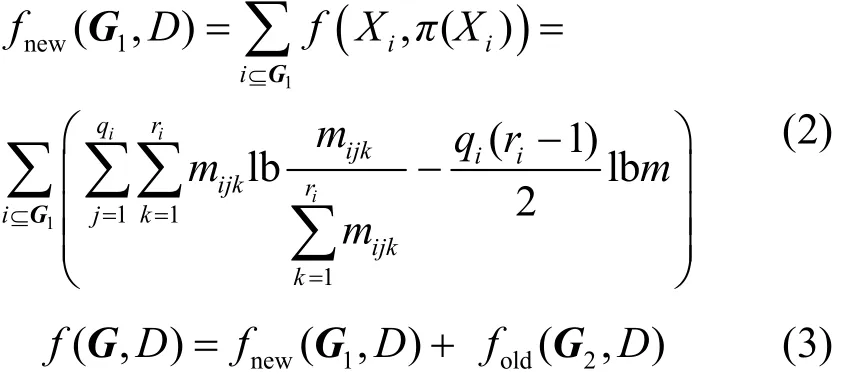
其中，Xi表示节点，π(Xi)表示Xi的父节点；mijk表示数据中满足π(Xi)组合，即取值为j且Xi=k的样本数；qi表示π(Xi)取值共有qi种组合；ri表示Xi共有ri种取值；D表示数据的样本；G表示邻接矩阵，G2表示G中未改变的局部结构，fold(G2,D) 表示G2的评分。

选取樽海鞘种群中高于平均评分的个体作为初始种群P0。文献[14]在种群划分阶段将初始种群随机分成2个相等的子种群更新个体，由于个体分布随着种群迭代动态变化，导致迭代后期无法提高算法的局部搜索能力。为了保证种群全局搜索与局部搜索的平衡，本文根据种群的进化情况建立自适应划分种群的规模因子q，具体的形式为

其中，NP为P0的种群规模，Tm为最大迭代次数，t为迭代次数，■*■为向下取整函数，K为自适应调整规模因子q的参数，是根据个体评分与该种群平均评分的相对值建立的，具体的形式为

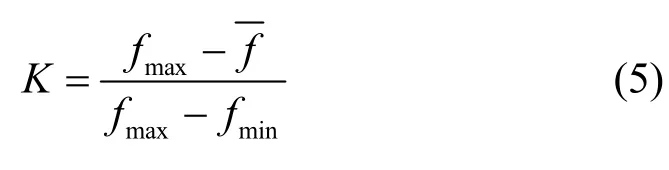
其中，fmax为P的最高评分值，f为P的平均评分值，fmin为P的最低评分值。

由于在迭代初期，种群的个体分布较分散，即K的值较小，因此q的值较小保证算法的全局搜索。随着迭代的进行，种群的个体分布趋于集中，即K的值也逐渐增大，因而q的值较大保证算法的局部搜索。

根据樽海鞘个体的评分将P0降序排列更新为种群P，利用规模因子q将种群划分为较好种群P1与较差种群P2，具体形式为

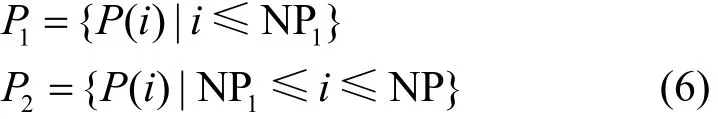
其中，P1的种群规模NP1=q，P2的种群规模NP2= N P- N P1。

2.2 子种群更新

为了提高HBSS-DE算法的收敛速度，利用自适应的变异算子与交叉算子改进 SSA的引领者与跟随者，建立樽海鞘搜索策略更新较好种群P1。同时为了提高算法的收敛精度，改进DE算法中的变异算子与交叉算子，建立差分搜索策略更新较差种群P2。

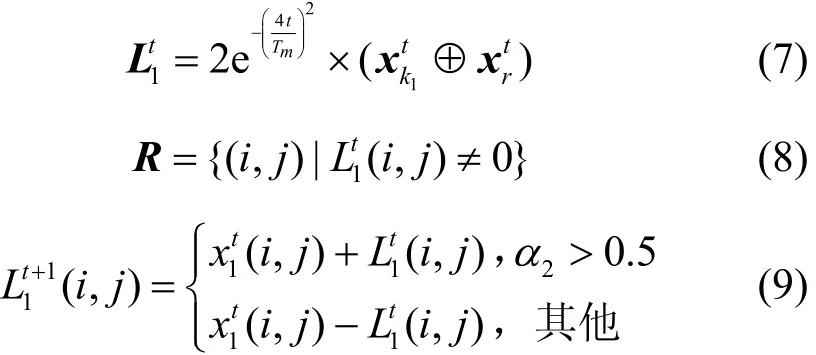
其中，rand为[0,1]之间的随机数，“1”为加边操作，“0”为减边操作为变异位置的值。

其中，Crmax为交叉概率上限；Crmin为交叉概率下限；M为控制交叉方式的参数，它是根据个体的差异，即当代种群中个体最佳评分与平均评分的相对值建立的，具体的形式如式(13)所示。

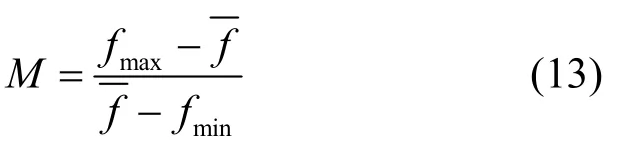
其中，fmax为P中最高评分值，为P的平均评分值，fmin为P中最小评分值。由式(13)可知，在算法的迭代初期，M的值较小，因而Cr的值较小，算法能以较大的概率选择单点交叉法更新个体。随着迭代的进行，M的值逐渐增大，Cr的值也逐渐增大，樽海鞘个体以较大的概率选择两点交叉法更新个体。

将自适应因子代入式(14)的交叉算子中更新P1中的跟随者个体即

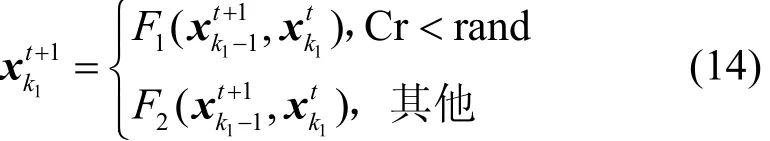
其中，F1是单点交叉，即随机选择一列的位置，然后交换 2个邻接矩阵对应列的位置；F2是两点交叉，即交换2个邻接矩阵对应两列的位置。以图2所示的单点交叉为例，交换矩阵A和矩阵C的最后一列，得到矩阵E。

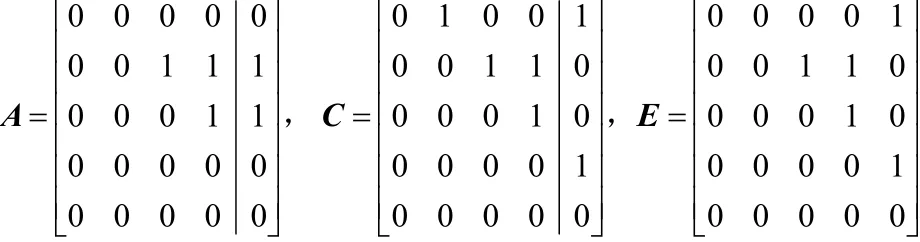
图2 单点交叉

1) 差分搜索策略

改进的变异算子先从P2中随机选取3个樽海鞘个体（其中），然后将代入式(15)产生差分矩阵根据式(8)得到的变异位置集合R。利用式(16)将中的变异位置值转化为变异概率并代入式(17)得到的变异位置值

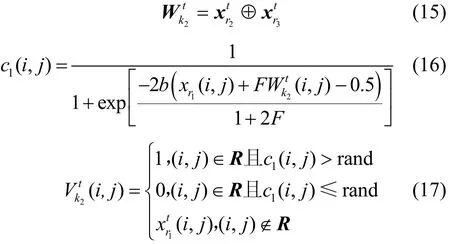
其中，k2⊆ [ 1,NP2]；r1、r2、r3为 [1 ,NP2]之间的随机整数，并且r1≠r2≠r3；rand为 0～1的随机数；c1(i,j)为变异概率；b=20为带宽因子[17]；F=0.5为

改进的交叉算子是通过式(12)得到P2的自适应因子Cr，代入式(18)将变异个体与原个体交叉得到更新个体即

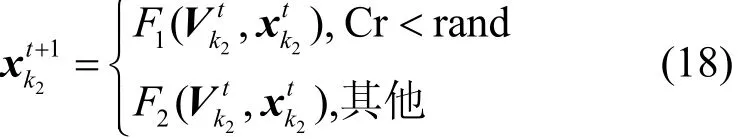
2) 选择操作

2.3 合并子种群

为了能够用更少的时间搜索到最佳网络结构，文献[14]将更新之后的子种群P1、P2合并为种群P，使种群中的个体在搜索空间中彼此共享位置信息。但是种群个体的分布情况是动态变化的，即在算法的迭代初期，个体分布比较分散，种群P1、P2中相同的个体较少；随着迭代的进行，个体趋于集中，种群P1、P2中相同的个体也逐渐增多，种群P的多样性易丧失。

由于迭代后期种群的多样性遭到破坏，算法易陷入局部最优。为保证算法迭代后期有能力跳出局部最优，本文将种群P1、P2中相同的个体通过两点变异增加种群的多样性。根据式(20)将P2中与P1评分相同的个体保存到种群P3，评分不同的个体保存到种群P4。

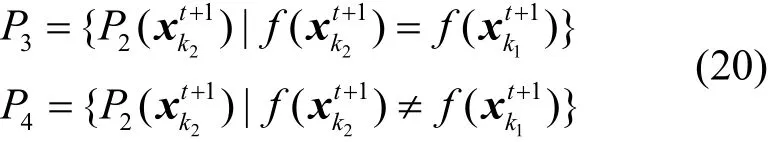
其中，k1⊆ [ 1,NP1]，k2⊆ [ 1,NP2]，f(xk

t1+1)、f(xk

t+21)分别是种群P1、P2中每个个体的评分。

将P3中的个体通过两点变异增加种群多样性，其中两点变异是对邻接矩阵中任意一列的2个元素进行取反，如图3所示对矩阵Q的右上角2个元素进行取反，得到矩阵W。

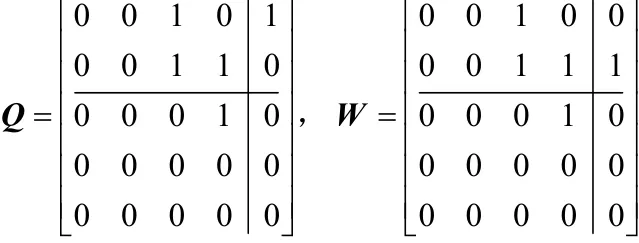
图3 两点变异

将更新种群3P与1P、4P合并成新的种群0P，根据个体评分降序排列更新种群P，利用规模因子重新划分种群进入下一次迭代。迭代结束后保留种群P中的评分最佳的樽海鞘个体，即最优的贝叶斯结构。

2.4 HBSS-DE算法的整体流程

本文2.1节～2.3节介绍了算法的原理，接下来，对算法的具体步骤进行简要描述。

步骤1 输入数据样本，通过互信息建立最大支撑树，初始化参数Tm，t=1。

步骤2 利用爬山算法对最大支撑树进行初步搜索得到樽海鞘种群，并选择高于平均值的樽海鞘个体建立初始种群0P。

步骤3 将0P通过评分降序排序更新为种群P，并通过自适应因子划分种群P为较好种群1P与较差种群2P。

步骤4 种群1P中采用樽海鞘搜索策略进行更新，提高算法的收敛速度。

步骤5 种群P2中采用差分搜索策略进行更新，提高算法的收敛精度。

步骤6 将2个子种群中相同个体利用两点变异增加种群的多样性，变异操作之后合并为种群P0。

步骤7 若满足t＜Tm，则t=t+1，并转至步骤3；否则，输出最高评分值对应的贝叶斯结构。

2.5 HBSS-DE算法的收敛性分析

根据 Solis等[18]提出的概率测度法分析随机搜索算法HBSS-DE的收敛性。

引理1 随机搜索算法 HBSS-DE满足f(N(z,ξ) ) ≥f(z)，若ξ∈Sgbest，则f(N(z,ξ) ) ≥f(ξ)。其中，f为HBSS-DE算法解决最大化问题的适应度函数；N为产生较优最新解的算子；z为搜索空间S的最优解空间Sgbest中的樽海鞘个体，也是在Sgbest上产生可接受函数值的上确界；ξ为算法在S上随机生成的樽海鞘个体。

证明根据 2.2节中选择操作的描述，可将HBSS-DE算法中对当前最优解的选择算子N定义为

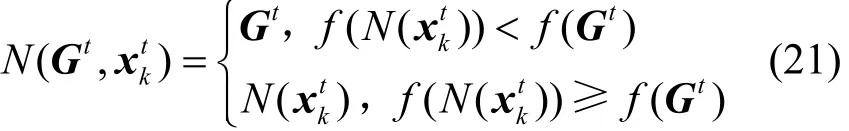
引理2 HBSS-DE算法的最优解空间Sgbest的概率测度大于0，即

证明假设HBSS-DE算法的贝叶斯结构群为X={x1,x2,…,xn} ,x∈S，其中搜索空间S是可列集或有限集，显然它的 Lebesgue[19]总是大于 0，即L[S] ＞0 ，HBSS-DE算法的最优解空间Sgbest属于S的一个Borel[19]子集，由HBSS-DE算法的最优解空间Sgbest的定义可知，证毕。

引理3 HBSS-DE算法中，当满足L[Sgbest]＞0时，式(22)成立。

其中，μt(∗)为第t次迭代结果的概率测度。

证明当满足L[Sgbest] ＞0时，有0＜μi,t(Sgbest)＜1，可知由μt产生的对Sgbest的概率测度为

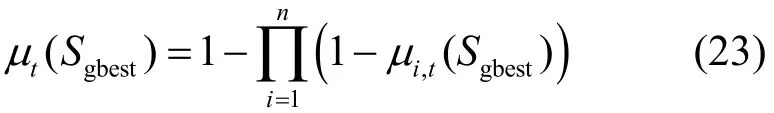
将μt(Sgbest)代入式(22)，可得

至此，引理3得证。根据Solis等[18]提出的概率测度法可知，当HBSS-DE算法满足引理1～引理3时，式(25)成立。其中表示在第t次的结果xt落到Sgbest里的概率值为1，即算法经过有限次迭代后，HBSS-DE算法中一定有存在于Sgbest的个体。寻找到最优解空间Sgbest之后，根据HBSS-DE算法的迭代性原则，在以后的所有迭代中，种群中所有个体都向Sgbest靠拢，最终收敛于Sgbest。

3 实验仿真

为了验证HBSS-DE算法的性能，在操作系统为Windows7，处理器为Intel i3 3.40 GHz CPU，内存为4 GB，软件环境为Matlab 2010a，基于贝叶斯网络工具箱 FullBNT-1.0.7中的 ASIA网络、CAR网络、ALARM网络进行仿真实验。其中，标准的ASIA网络具有8个节点、8条边，标准的CAR网络具有12个节点、9条边，标准的ALARM网络具有37个节点、46条边。3种标准网络是通过训练实际数据建立的贝叶斯网络，其中节点之间的边表示因果关系。在3种网络中随机生成数据量为500、1 000、3 000、5 000个的数据样本，因为数据是随机产生的，为降低数据的随机性对实验结果准确性的影响，每种样本容量分别产生 10个，且每个数据单独运行10次，即每组数据运行100次后取平均值作为实验结果。

随着节点的增加，采用评分搜索的方法学习全局最优解是一种 NP问题[7]，而全局最优解与较其稍差的局部最优解的实际效益相差不大[18]，因而采用足够好的解Sgbest来代替全局最优解，将NP问题转化为N-问题。HBSS-DE算法在3种网络中的实验结果分别如表1～表3所示，其中fbest是100次实验中的最佳BIC评分，fav是100次实验的平均BIC评分，fsn是标准网络的BIC评分。利用验证算法的局部最优解Sgbest是否接近全局最优解。

由表1～表3可知，在小网络（如ASIA网络、CAR网络）中，当数据量＞500个时HBSS-DE算法搜索到的最佳结构评分fbest与标准网络的评分fsn几乎相同，即在小网络中可以搜索标准网络，这是因为小网络中节点较少、搜索空间较小。而在大网络中（如ALARM网络），HBSS-DE算法的fbest比较接近fsn，这是因为随着节点的增多，搜索空间变大，算法收敛于接近全局最优解的局部最优解。在ASIA网络中σ的平均值为0.004 91，在CAR网络中σ的平均值为0.010 4，在ALARM网络中σ的平均值为0.023 9，总体而言HBSS-DE算法的局部最优解Sgbest接近全局最优解。

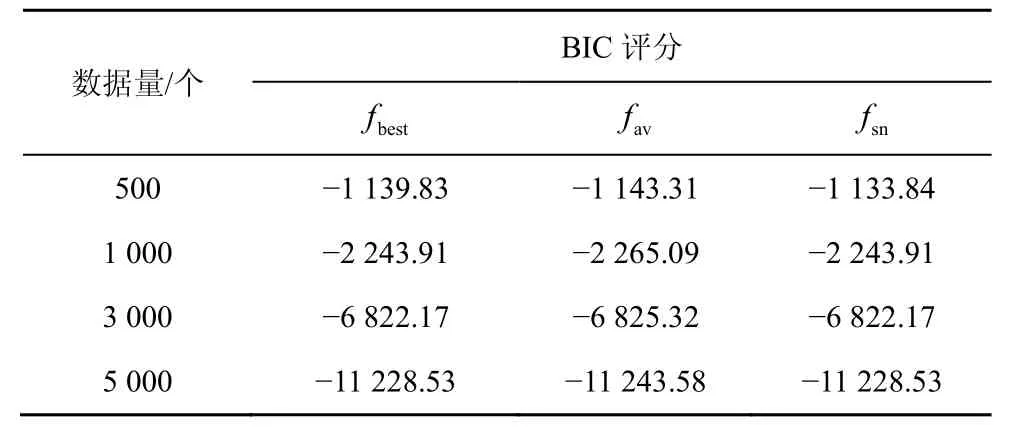
表1 ASIA网络HBSS-DE算法的BIC评分

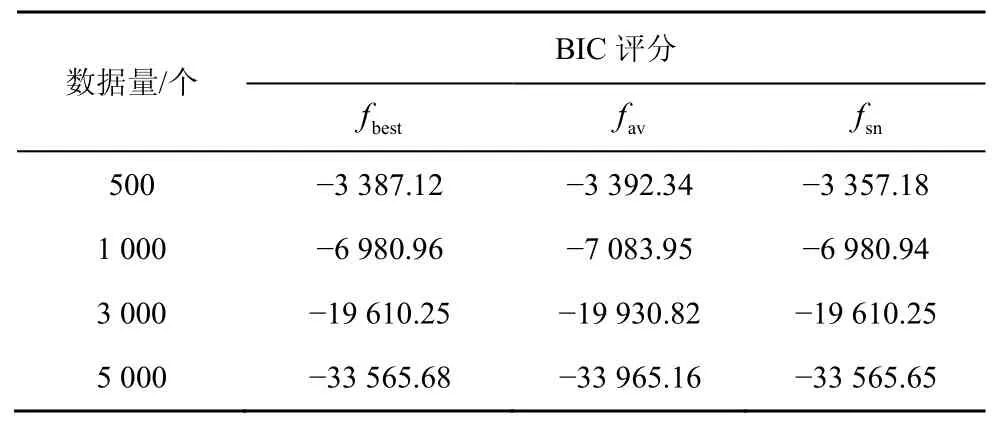
表2 CAR网络HBSS-DE算法的BIC评分

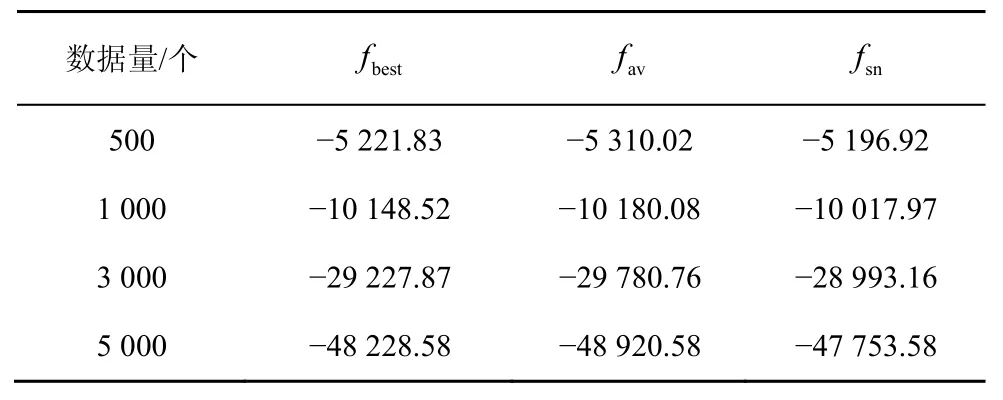
表3 ALARM网络HBSS-DE算法的BIC评分

根据文献[21]，列出分析算法性能的评价指标。

Ext（execution time）：找到最佳网络所需要的时间（单位为s）。

TP（true positive）：真正例，即预测结构与标准结构中相同且方向为正的边。

FP（false positive）：假正例，即预测结构中边的方向为正，标准结构中为负。

FN（false negative）：假负例，即预测结构中边的方向为负，标准结构中为正。

TPR（true positive rate）：正确率，即预测结构中TP与标准结构中边的比值，

FPR（false positive rate）：精确率，即预测结构中TP与预测结构全部边的比值，

F（F-measure）：综合评价指标，即正确率和召回率的调和平均值，

W：100次实验中HBSS-DE算法的实验值ψ与其他算法的实验值ε相比提升的百分比，即

将 HBSS-DE算法与 AESL-GA、MAK、BEWCA-BN、MMHC算法进行对比实验。其中本文算法自适应因子的上下限分别为0.85、0.2。根据文献[1]设BEWCA-BN尺度因子c的上下限分别为0.9、0.7，搜索强度参数d的上下限分别为0.2、0.01。根据文献[7]设 MMHC独立性测试的置信度α为0.01，统计阈值设置为0.05。根据文献[8]设MAK信息素强度系数为 1，信息素蒸发系数为 0.7，启发式因子权重为2。根据文献[9]设AESL-GA独立性测试的置信度为0.01，精英个体阈值α为0.09。实验结果如下：表4～表6是不同算法在不同网络的平均BIC评分，图4～图6是不同算法在不同网络的结构对比，表7～表9是不同算法在不同网络的执行时间对比。

由表4～表6可知，当数据量为500时，在ASIA网络与CAR网络中，本文算法和BEWCA-BN算法均能找到相对较优的评分，但随着数据量的增大，本文算法相比于其他算法能学习到更优的评分。根据W计算，当数据量为500、1 000、3 000、5 000时，本文算法与其他算法相比，BIC评分的平均提高值分别为然后利用得到整体 BIC提升百分比。本文算法在 ASIA网络中的 BIC评分比MAK、MMHC、AESL-G、BEWCA-BN 算法平均提升了 3.71%、4.34%、3.85%、1.86%，在 CAR网络中平均提升了4.41%、3.64%、2.49%、1.47%，在 ALARM 网络中平均提升了 6.96%、9.08%、10.02%、3.84%。总体而言，HBSS-DE算法能够找到评分更优的贝叶斯网络结构，在大型网络中比其他算法的提升效果更佳。这是由于本文算法可以在较好个体周围局部搜索，在较差个体周围全局搜索，并通过规模因子保证了算法的局部搜索与全局搜索的平衡，即在迭代前期全局搜索，迭代后期局部搜索。同时对于2个子种群中相同个体利用两点变异策略增加了种群的多样性，避免陷入局部最优。

表4 不同算法在ASIA网络中不同数据量下的平均BIC评分

表5 不同算法在CAR网络中不同数据量下的平均BIC评分

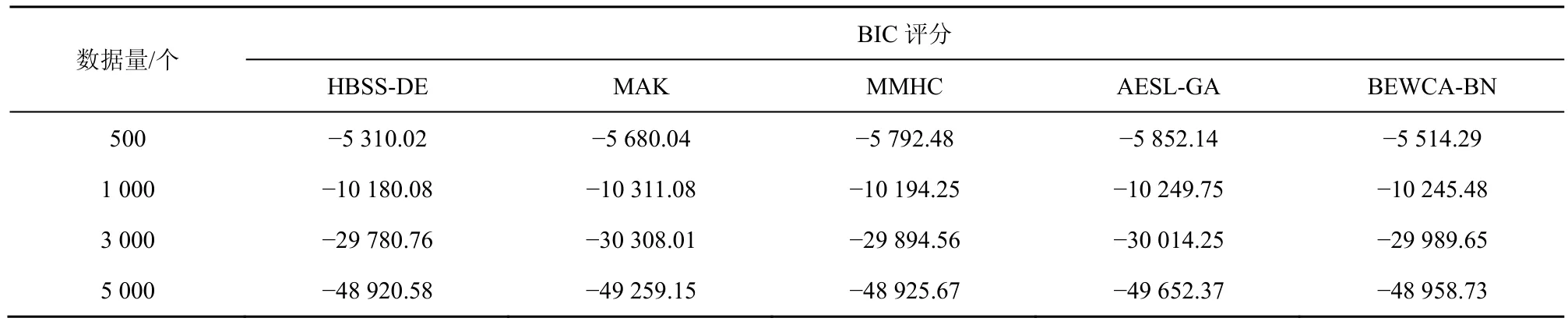
表6 不同算法在ALARM网络中不同数据量下的平均BIC评分

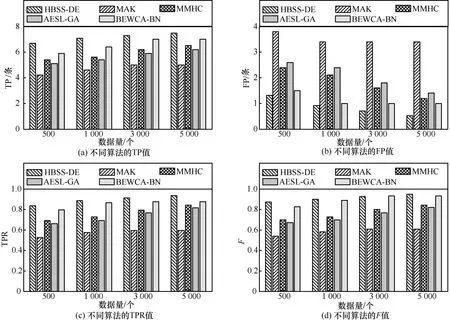
图4 ASIA网络不同数据下的结构对比

图5 CAR网络不同数据下的结构对比

图6 ALARM网络不同数据下的结构对比

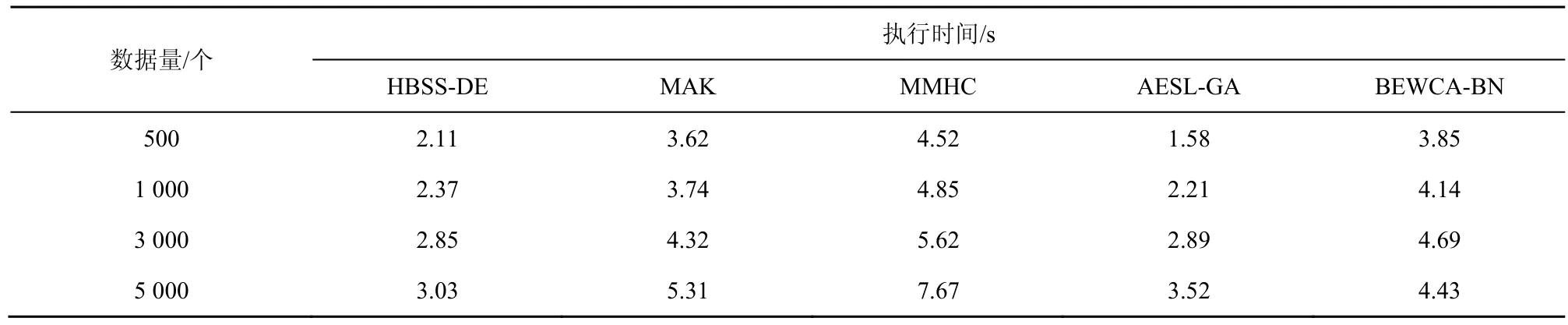
表7 不同算法在ASIA网络中不同数据量下的执行时间

表8 不同算法在CAR网络中不同数据量下的执行时间

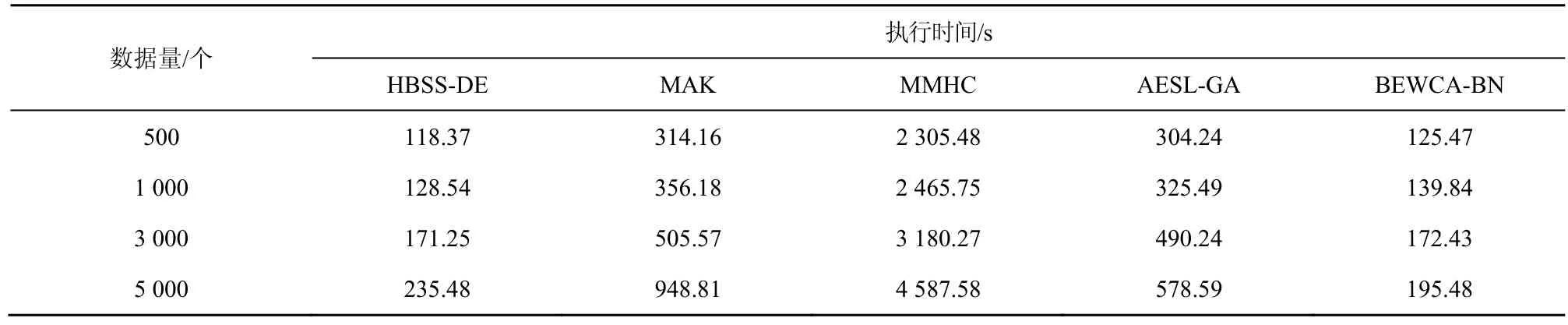
表9 不同算法在ALARM网络中不同数据量下的执行时间

由图4～图6可知，本文算法的TP值在ASIA网络中比MAK、MMHC、AESL-GA、BEWCA-BN算法平均多了1.49、1.34、1.02、0.79，在CAR网络中比其他算法平均多了2.21、1.71、1.23、0.56，在ALARM网络中比其他算法平均多了7.41、4.11、4.81、3.65。本文算法在ASIA网络、CAR网络、ALARM 网络中 FP的值均小于其他算法，且在 3个网络中的TPR值均大于其他算法。根据W计算，当数据量为500、1 000、3 000、5 000时，本文算法与其他算法相比，F值平均提高的百分比分别为然后利用计算整体提高百分比。本文算法的F值在ASIA网络中比MAK、MMHC、AESL-GA、BEWCA-BN算法平均提高了22.54%、17.89%、15.17%、8.57%，在CAR网络中比其他算法平均提高了25.74%、19.29%、13.32%、9.64%，在 ALARM 网络中比其他算法平均提高了24.71%、15.19%、10.91%、6.36%。总体而言，HBSS-DE算法能够找到更准确的贝叶斯网络结构，这是由于在较差种群中采用差分搜索策略，即在较差个体周围进行全局搜索增加了种群的多样性；通过自适应因子保证种群在迭代前期的全局搜索能力强；同时合并子种群时的两点变异增大种群的搜索范围，增加了种群跳出局部最优的能力。

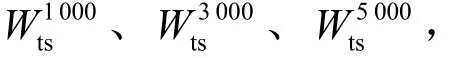
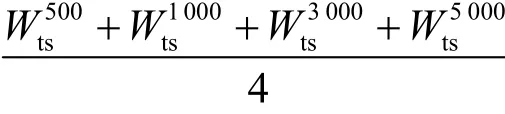
由表7～表9可知，当ASIA网络的数据量为500和1 000时，AESL-GA运行时间最短，HBSS-DE算法运行时间比AESL-GA略长一些，这是由于在小数据量下HBSS-DE算法为了提高算法的全局搜索，通过规模因子将种群划分为2个子种群更新个体，并将子种群中相同的个体利用两点交叉变异扩大搜索的范围。虽然避免了陷入局部最优，但同时增加了运行时间。根据W计算，当数据量为500、1 000、3 000、5 000时，HBSS-DE算法与其他算法相比，执行时间平均缩短的百分比分别为其整体缩短的百分比根据得到。与MAK算法、MMHC算法、BEWCA-BN算法相比，HBSS-DE算法在 ASIA网络中的运行时间平均缩短了15.25%、21.77%、5.32%。在CAR网络中，HBSS-DE算法比 MAK、MMHC、AESL-GA、BEWCA-BN算法平均缩短了18.57%、13.26%、15.18%、5.12%。当ALARM网络数据量为5 000时，HBSS-DE算法比BEWCA-BN算法耗时略长，这是由于节点较多的网络搜索的范围较大，在迭代的过程中差分搜索策略虽然增大了搜索的空间，提高了算法的全局搜索能力；合并子种群时的两点交叉变异虽然增加了种群的多样性，避免了算法陷入局部最优，但是差分搜索策略与两点交叉变异也增加了算法的搜索时间。HBSS-DE算法在ALARM网络中比MAK、MMHC、AESL-GA、BEWCA-BN算法平均缩短了28.23%、92.63%、19.04%、1.42%。总体而言，HBSS-DE算法在大型网络中比其他算法的搜索效率的优势更明显。这是因为樽海鞘搜索策略的局部搜索能力强，能够快速地收敛到最优解。而自适应因子保证了迭代后期的局部搜索，提高了搜索效率；同时在评价个体时仅计算个体改变的部分结构，减少在评价个体时消耗的无用时间。

4 结束语

本文提出了基于混合樽海鞘-差分算法的贝叶斯网络结构学习算法HBSS-DE。该算法通过设置规模因子，将种群划分为2个子种群，利用构建的樽海鞘搜索策略与差分搜索策略分别更新不同的子种群，在合并子种群时利用两点交叉变异增加种群的多样性。仿真实验证明，HBSS-DE算法能够找到最佳的贝叶斯网络结构，其中规模因子平衡了局部搜索与全局搜索，樽海鞘搜索策略提高了算法的寻优效率，差分搜索策略提高了算法的收敛精度。与其他算法相比，HBSS-DE算法的收敛精度与寻优效率均有提升。