双重介质低渗透油藏水平井试井模型
姜瑞忠,张福蕾,杨 明,乔 欣,张春光
(1.中国石油大学(华东),山东 青岛 266580;2.中海石油(中国)有限公司天津分公司,天津 300452;3.中国石油北京油气调控中心,北京 100007)
0 引 言
近年来,中高渗油藏在中国油气资源产出所占的比重越来越低,低渗透油藏对增储上产起到更加关键的作用,合理高效地开发低渗透油藏成为研究人员关注的热点。前人在研究低渗透油藏试井问题时,大多数考虑拟启动压力梯度[1-6]和应力敏感性[7-12],而拟启动压力梯度模型采用不过原点的直线代替曲线,忽略了低压力梯度下流体的流动能力。袁英同等[1]提出了基于低速非达西渗流模式的固定边界数学模型,并讨论了流动边界和启动压力梯度的影响;蔡明金等[2]考虑启动压力梯度、应力敏感性,建立了低渗透均质油藏试井解释模型;刘永良等[3]建立了考虑启动压力梯度的双重介质低渗透油藏数学模型;姜瑞忠[13]等基于毛细管模型和边界层理论提出了低渗透油藏新的渗流模型,其很好地解释了启动压力梯度和非线性渗流的存在。目前,利用FEM数值方法求解的同时考虑非线性系数和应力敏感性的低渗透油藏水平井压力动态分析方法鲜有报道,因此,针对这一问题进行研究。通过绘制典型曲线对各类相关参数进行敏感性分析,并对现场区块的实测压力数据进行拟合。研究成果对于提高低渗透油藏的开发效果具有一定的理论指导意义。
1 模型建立
1.1 物理模型
建立圆形双重介质储层水平井物理模型,模型假设为:双重介质储层由基质系统和裂缝系统组成,基质和裂缝间的窜流视为拟稳态,液体先从基质流入裂缝后再进入水平井井筒,即Warren-Root模型;油藏外边界为封闭边界或定压边界,储层水平且厚度一致,储层渗透率各向异性,水平井位于油藏中心,产量恒定,只考虑裂缝系统的应力敏感性,忽略重力和毛细管力的影响,考虑井筒储集效应和表皮系数。
1.2 数学模型
流体在低渗透油藏中渗流不再遵循达西模型,根据边界层理论和毛细管渗流模型,采用文献[14]中的低速非线性渗流方程:
(1)
式中:v为渗流速度,cm/s;K为渗透率,mD;μ为原油黏度,mPa·s;▽p为驱动压力梯度,10-1MPa/m;c1、c2为非线性系数,MPa/m;δLV为非线性变量。
其中,c1表示边界层和屈服应力值的影响,c2仅反映边界层的影响,二者可通过岩心渗流实验拟合获得,拟合结果表明c1>0,c2<0。
直角空间坐标系中,由连续性方程、运动方程和状态方程得到的渗流控制方程为:
(2)
β=Kfv/Kfh
(3)
式中:Kfh为裂缝水平方向渗透率,mD;Kfv为裂缝垂直方向渗透率,mD;x、y、z为空间坐标;αK为渗透率模数,MPa-1;pi为原始地层压力,MPa;pf为裂缝系统压力,MPa;pm为基质系统压力,MPa;φf为裂缝系统孔隙度;Cft为裂缝系统压缩系数,MPa-1;t为时间,s;σ为形状因子,1/m2;Km为基质渗透率,mD;i为初始条件。
(4)
式中:φm为基质系统孔隙度;Cmt为基质系统的压缩系数,MPa-1。
初始条件为:
pf(x,y,z=0)=pi
(5)
封闭外边界条件为:
(6)
式中:re为外边界的半径,m;ze为顶边界z方向的坐标,m。
定压外边界条件为:
pf(r=re)=pf(z=ze)=pi
(7)
定义无因次变量:
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
式中:L为水平井半长,m;zw为井中心z方向的坐标,m;rw为井半径,m;h为储层厚度,m;Q为水平井产量,m3/d;B为体积系数;Kv为垂直方向渗透率,mD;Kh为水平方向渗透率,mD;C为井筒储集系数,m3/MPa;ω为弹性储容比;λ为窜流系数;lc为特征长度,m。
由式(2)—(23)建立的双重介质低渗透油藏无因次水平井渗流数学模型为:
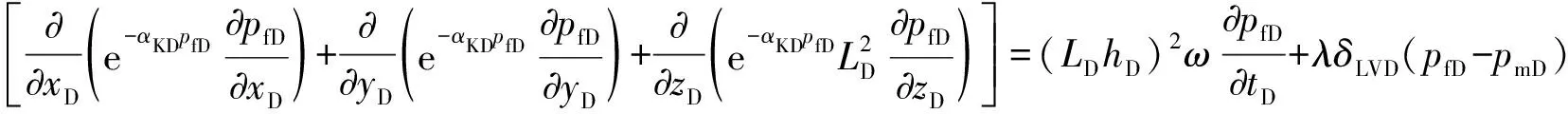
(24)

(25)
pfD(xD,yD,zD,tD=0)=0
(26)
(27)
pfD(rD=reD)=pfD(zD=0,1)=0
(28)
2 模型求解
采用隐式求解裂缝系统,显式求解基质系统的方法。
2.1 裂缝系统
使用Galerkin方法得到不考虑源/汇项的有限元方程,再通过格林函数得到的内部单元和封闭边界单元的有限元方程为:
(29)


(30)
(31)
(32)
式中:Nj为形函数(j=1,2,3,…);Ωe为单元域;V为单元域体积;ΔtD为无因次时间步长;n为某时刻的时变量值;Ke为非线性系数矩阵,求解时给Ke初始值并线性化后再求解压力解。
2.2 基质系统
利用相同的方法得到单元有限元方程矩阵形式的简化形式为:
(33)
(34)
(35)
窜流项的处理采用同一时间步的裂缝系统求解结果。将水平井视为均匀流量线源,所在网格引入单元内源汇项,应用Delta函数获取与水平井位置相关的线源汇方程。
(36)
式中:m为水平井划分结点的数量;δ为Delta函数;x0,y0,z0为结点坐标。
因此,单元源汇项的有限元方程为:
(37)
无因次形式为:
(38)
利用离散数据点拉氏变换法,将实空间中压力的数值解转换到拉氏空间中,从而将井筒储集系数和表皮系数引入压力公式中。
(39)
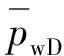
利用Stehfest数值反演方法得到实际空间中的无因次压力。
3 结果验证及敏感性分析
3.1 结果验证
当非线性系数c1D=0、c2D=0,渗透率模数αKD=0时,将计算出的数值解与李晓平等[14]的解析解进行比较,数值解与解析解的曲线结果一致,证明建立的模型是可靠的(图1)。
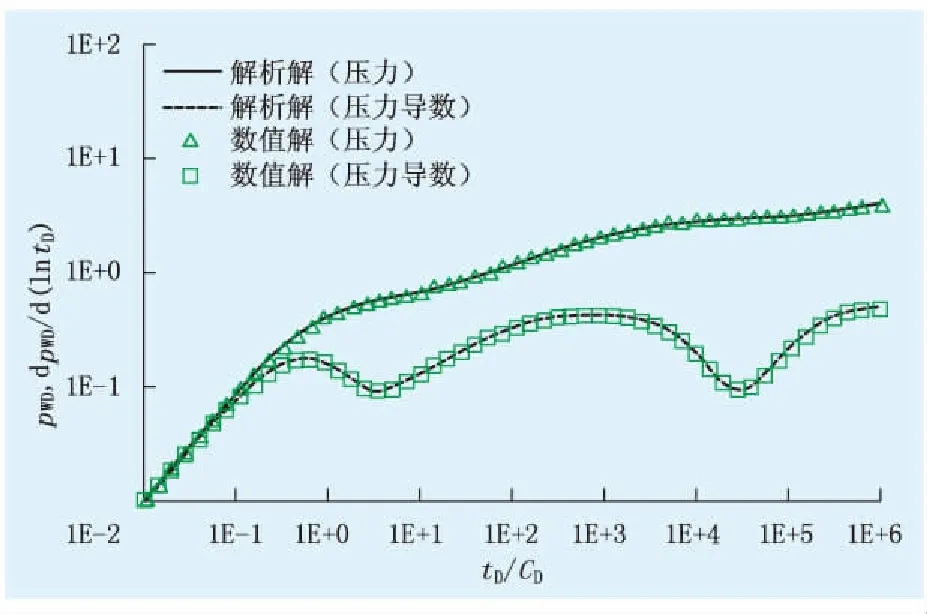
图1 数值解的验证
3.2 典型图版
绘制不同模型的水平井压力及压力导数曲线(图2,CD=100,s=0,LD=5,hD=200,λ=0.05,ω=0.05)。达西模型中c1D=0.0,c2D=0.0,αKD=0.0,应力敏感性模型中c1D=0.0,c2D=0.0,αKD=0.1,非线性模型中c1D=0.2,c2D=-0.2,αKD=0.0,考虑应力敏感性和非线性渗流的2个因素模型中c1D=0.2,c2D=-0.2,αKD=0.1。
考虑应力敏感性时,压力及导数曲线上移,压力导数曲线值大于0.5,偏离了达西模型下中期和晚期径向流的水平段,随着时间的推移,偏差的程度变大。考虑非线性渗流时,压力导数曲线的“凹子”变浅,并向右移动。与非线性系数相比,应力敏感性对曲线的影响更加显著。
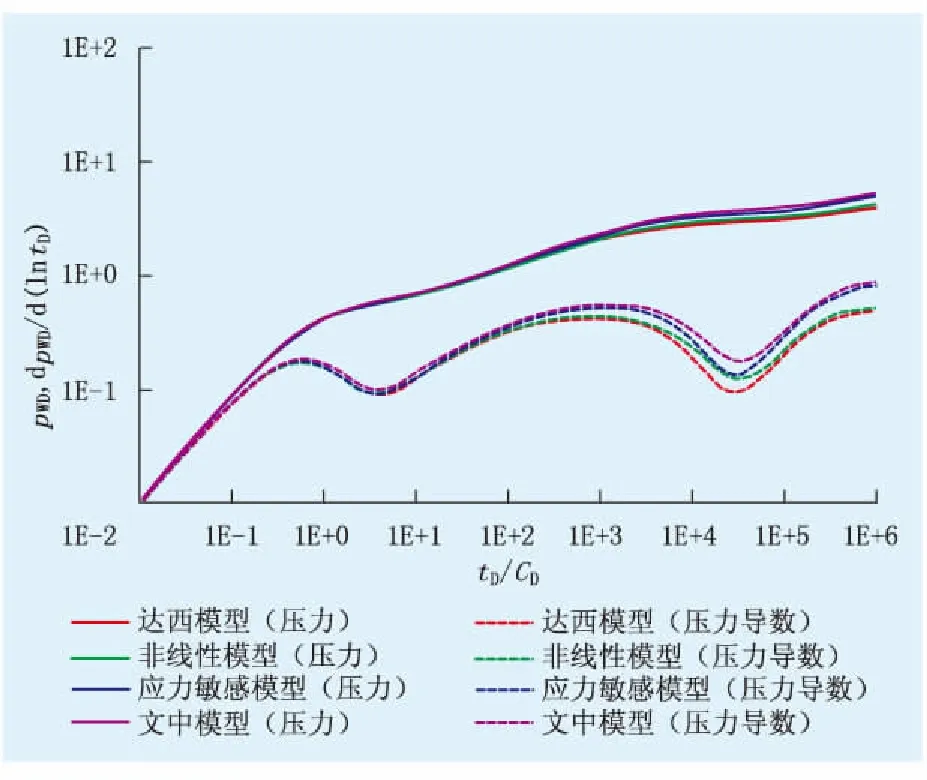
图2 不同模型的试井典型曲线
3.3 敏感性分析
3.3.1 非线性系数c1D、c2D对试井曲线的影响
非线性系数作用于从基质到裂缝的非线性流动阶段,c1D或c2D增大时,最小启动压力梯度增大,窜流减弱。c1D主要影响压力导数曲线“凹子”的深度和位置,当c1D增大时,“凹子”变浅,出现变晚(图3);非线性系数c2D影响“凹子”的深度,当c2D增大时,“凹子”上移(图4)。
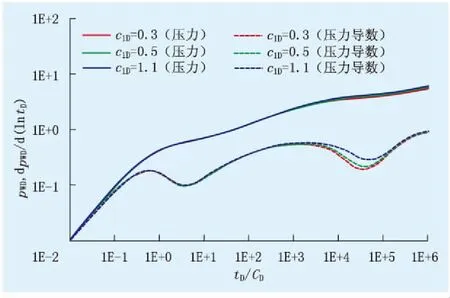
图3 非线性系数c1D对试井曲线的影响
3.3.2 渗透率模数对试井曲线的影响
应力敏感性主要导致曲线在井筒储存阶段上移,随着渗透率模数的增加,曲线后期上翘更加严重,“凹子”的深度和位置不变。因为当应力敏感性增强时,渗透率的损害更加严重,流体流动变得更加困难,所需的压降更大(图5)。
3.3.3 窜流系数对试井曲线的影响
窜流系数表征流体从基质到裂缝的窜流能力。窜流系数越大,窜流阶段出现越早,“凹子”向左移动,其大小和深度保持不变。较大的窜流系数表示基质和裂缝之间的物理性质差异较小,窜流更容易发生。由于应力敏感性的影响,“凹子”出现时间不同,窜流系数增大,“凹子”最低点的高度下降。压力及导数曲线在晚期径向流阶段重合(图6)。

图4 非线性系数c2D对试井曲线的影响

图5 渗透率模数对试井曲线的影响
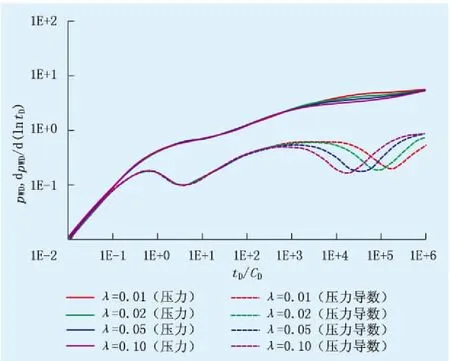
图6 窜流系数对试井曲线的影响
3.3.4 顶底边界对试井曲线的影响
当顶底边界非封闭时,井筒储存阶段后的流动阶段消失。当压力波传播到定压边界后,压力变为恒定且压力导数迅速下降,混合边界导数下降晚于定压边界(图7)。

图7 顶底边界对试井曲线的影响
4 实例应用
对南海西部文昌油田一口水平井的压力测试数据进行分析,油藏厚度为10.8 m,孔隙度为0.241,渗透率为24.5 mD,原油黏度为1.33 mPa·s,总压缩系数为2.215×10-3MPa-1。利用模型得到的理论曲线与实测曲线进行拟合,拟合程度高(图8),该研究对低渗透油藏试井分析有很好的指导作用。
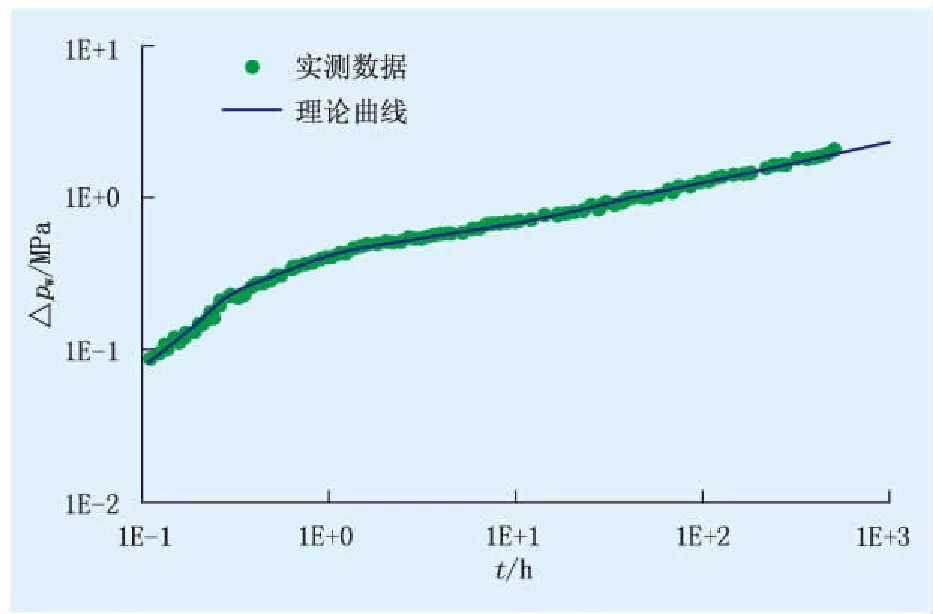
图8 理论曲线与实测曲线拟合结果
5 结 论
(1) 建立的双重介质低渗透油藏水平井数学模型可以研究非线性系数和应力敏感性对试井曲线的影响,实现了FEM数值方法求解数学模型。
(2) 试井典型曲线显示数值解与解析解的曲线结果一致,分析非线性系数、渗透率模数、窜流系数、顶底边界等各类参数敏感性,实际区块压力数据与理论曲线可以良好拟合。
(3) 考虑应力敏感性时,压力导数曲线值大于0.5,偏离了达西模型下中期和晚期径向流的水平段,偏差程度随时间推移增大。考虑非线性渗流时,压力导数曲线的“凹子”变浅,且向右移动。与非线性系数相比,应力敏感性对曲线的影响更加显著。

