一种基于机器学习的有利区评价新方法

李克文，周广悦，路慎强，郭 俊

(1.中国石油大学(华东)，山东 青岛 266580；2.中国石化胜利油田分公司，山东 东营 257022)

0 引 言

目前，中国大部分油田处于勘探开发中后期，探明储量以隐蔽性油藏为主，但隐蔽性油藏较难被发现[1]，因此，有利区预测是勘探开发过程中非常关键的一步[2]。传统的有利区预测一般基于断层、地貌等地质信息或者根据少量常用的地震属性参数建模[3]，许多学者在该方面进行了深入的研究，主要以地震、测井等资料为基础，分析构造特征以及油藏特征，利用参数分析法、AVO属性分析法等完成储层综合评价，以此为依据进行有利区预测[4-7]。传统预测方法由于地质条件复杂、采用的地震属性相关性差、井震匹配关系差，导致预测精度低。随着地球物理技术的进步和发展，利用机器学习进行有利区预测的方式应运而生[8-11]。机器学习中考虑到地震属性之间的隐含作用，筛选出对分类起积极作用的关键地震属性，解决了多解性问题，从而辅助地质人员快速圈定有利目标。以东营某区域地震体为例，该区域的已钻井数量较少，还未对有利区进行充分的挖掘，采用岭回归与逻辑斯谛分类算法相融合的模型，通过对地震属性集进行相关性分析，选择能反映有利区的关键属性，进而预测有利区分布。

1 研究方法与原理

1.1 岭回归

地震属性集[12]中可能存在大量冗余以及无关的属性，使用特征提取算法[13]对属性集进行约简，降低属性集的维度，避免有害属性对分类结果产生影响，使得预测结果更加准确。文中使用正则化-岭回归进行属性约减。

正则化即在已有模型的最小化经验误差函数上加上额外的约束或者惩罚项，该约束或惩罚项可以理解为对参数引入先验分布。误差函数由原来的E(X，Y)变为E(X，Y)+alpha‖w‖，其中X为输入变量，Y为输出变量，w为模型系数组成的向量，‖‖为L1或者L2的范数[14]，alpha为一个可调参数，控制正则化的强度。当正则化用在线性模型上时，L1正则化和L2正则化也称为Lasso和Ridge。

L2正则化将模型系数w的L2范数添加到了误差函数中，其中惩罚项中系数为二次方，因此，L2正则化会让系数的取值变得平均。关联性大的特征，对应系数相近[15]。用于特征选择时，L2是一种相对稳定的模型，对于特征理解来说更加有用[16]：能力强的特征对应的系数为非零。岭回归的损失函数为：

(1)

1.2 基于逻辑斯谛回归算法的多分类问题研究

简单的线性回归函数中每个训练数据对应一个假设值，该假设值是连续的，不能直接进行分类，在此函数基础上延伸，将概率和假设值结合起来进行分类，即逻辑斯谛回归算法[17-18]。

1.2.1 二项逻辑斯谛回归模型

二项逻辑斯谛回归模型是用于分类的模型，使用P(Y|X)表示，其中，随机变量X取实数，随机变量Y取1或0。该模型的条件概率分布分别为：

(2)

(3)

式中：x∈Rn，为输入；Y∈{0，1}，为输出；b为偏置；w·x为内积。

根据给定的输入值x，由上式求得P(Y=1|x)和P(Y=0|x)，通过比较2个条件概率值的大小，将x进行分类[19]。对于给定的训练集T=[(x1，y1)，(x2，y2)，…，(xN，yN)]，模型参数通过极大似然估计法得到，进而得到逻辑斯谛回归模型。

1.2.2 多项逻辑斯谛回归

将二项逻辑斯谛回归模型推广为多项逻辑斯谛回归模型。若定义离散型随机变量Y的取值集合为{1，2，…，K}，则多项逻辑斯谛回归模型为：

(4)

(5)

式中：x∈Rn+1；wk∈Rn+1。

2 实验结果及分析

2.1 实验数据

以东营某区域第4层位作为研究对象，从勘探数据库、地震数据体等数据源中提取目的层位的地震属性、井数据、岩性剖面数据、时深转换以及层位数据等井震信息，作为有利区预测的数据来源。

2.2 数据预处理

2.2.1 直井样本的获取

选择井口坐标最近的地震道A，提取该地震道对应的地震属性集，记作输入变量Xi={x1，x2，…，xn}，n为地震属性的个数；根据层位数据选取地震道A的时窗[t1，t2]；根据标定数的时深对，计算对应的深度范围[d1，d2]；统计[d1，d2]范围内砂岩的累计厚度，计算类别标签，有利区按照好、中、差分为3类，记作输出变量y={0，1，2}。

2.2.2 斜井样本的获取

斜井由于井眼轨道偏移，对应层位的地震道需要重新计算。根据井斜数据，逐点计算采样点对应的垂深、坐标方向偏移量[vd，Δx，Δy]；利用时深标定数据，计算νd对应于地震剖面上的时间st；利用Δx、Δy、井口坐标计算与采样点最近的地震道A。根据层位数据获取当前地震道A的时窗[t1，t2]，若stt1，则此时的地震道A即为该斜井目标层位在地下对应的地震道，再通过式(1)获取样本(Xi，y)。

2.3 特征选择实验结果分析

图1为岭回归算法筛选不同对应采收率地震属性。由图1可知，选择的特征个数为5时分类准确率最高，特征选择个数小于5时，分类准确率整体上呈现升高趋势，关键属性个数的增加提高了分类器的性能；特征选择个数大于5时，分类准确率整体上呈现下降趋势，无用属性以及冗余属性的增加降低了分类器的性能。由实验可知，分类准确率最高的5个关键属性分别为均方根振幅、瞬时相位、最小振幅、弧长、最大振幅。采用岭回归得到的关键属性基本包含了传统有利区预测常用的均方根振幅、瞬时相位、最小振幅、最大振幅等地震属性，同时筛选出的不常用属性弧长可作为下一步尝试用于有利区预测的地震属性。

图1 岭回归特征选择分类性能

表1为支持向量机递归特征消除、方差分析[20]、随机森林、Lasso回归[21]、岭回归等特征选择算法在逻辑斯谛回归、K近邻算法、决策树[22]、自适应增强算法[23]上的分类准确率比较。由表1可知，岭回归特征选择算法在逻辑斯谛回归、K近邻算法、决策树、自适应增强分类器上的准确率分别是57.5%、58.4%、52.4%、56.0%，且对比其他的特征选择算法，岭回归对应的分类准确率最高。由此说明岭回归特征选择不仅能够选择出比较好的关键特征，而且能够获得较高的分类性能。

表1 多种特征选择方法在不同分类器上的准确率

2.4 分类预测实验结果分析

2.4.1 采用多种分类算法进行对比实验

地震属性作为输入变量，其衡量的尺度有很大的差异，需要对其进行去均值及方差归一化处理。将经过标准化处理的地震属性作为分类模型的输入，采用交叉验证方法，计算多种带有默认参数分类算法的准确率、精确率、召回率以及F1值进行模型评估，选择分类效果最优的模型。

文中采用的分类算法包括逻辑斯谛回归、线性判别式分析、K近邻算法、决策树、朴素贝叶斯[24]等普通分类算法以及自适应增强算法、梯度提升决策树[25]、随机森林[26]、极端随机树、极端梯度提升等。

采用各个算法训练分类模型，计算不同算法对应的准确率、精确率、召回率以及F1值(表2、3)。普通分类算法中线性判别式分析、逻辑斯谛回归以及K近邻算法的准确率都达到了50.0%以上，集成分类算法中的梯度提升决策树、随机森林、极端梯度提升准确率较高，说明以上算法具有进一步研究的意义。

表2 普通分类算法性能指标

表3 集成分类算法性能指标

2.4.2 确定最优参数

选取分类效果比较好的几种算法的常用参数取值范围，采用网格搜索进行自动调参，使用交叉验证降低划分训练集造成的偶然性，获得平均准确率最高的参数组合。最优参数的选择结果如表4所示。

表4 分类器最优参数

由表4可知，经最优参数选择后的K近邻算法、梯度提升决策树以及逻辑斯谛回归的准确率最高。

2.4.3 选择最优的分类算法

利用表4中的K近邻算法、梯度提升决策树以及逻辑斯谛回归最优参数算法对数据样本进行重新训练，采用交叉验证，随机选择种子，保证分类结果的准确性。各训练模型的分类算法指标如表5所示。

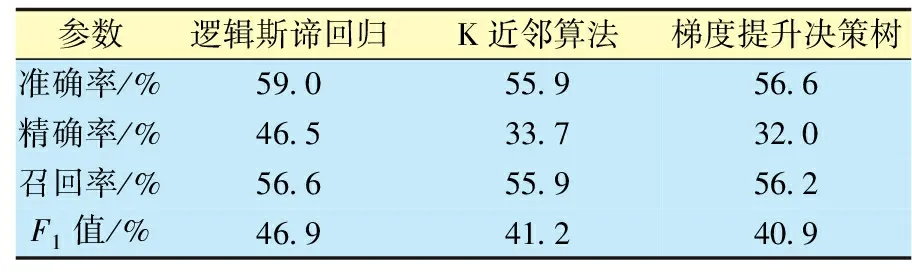
表5 优选分类算法性能指标

综上所述，逻辑斯谛回归分类算法准确率最高，达到60.0%左右，且精确率、召回率以及F1值相对于其他算法也是最高的，因此，确定为最优算法。

2.5 采用岭回归+逻辑斯谛回归预测有利区

将预处理后的地震属性集作为输入，采用岭回归筛选出关键地震属性集，包括均方根振幅、瞬时相位、最小振幅、弧长、最大振幅，将其作为逻辑斯谛回归模型的输入，进而训练分类模型，该融合模型的分类准确率为61.5%，精确率为48.5%，召回率为60.1%，F1值为48.5%。实验结果表明，利用岭回归与逻辑斯谛分类相融合的算法，分类准确率达到60%以上，预测效果明显。

图2为对东营某区域进行预测的二维结果俯视图，其中绿色区域代表非有利储层发育区(标签为0)，黄色区域代表储层发育区(标签为1)，红色区域代表有利储层发育区(标签为2)，蓝色表示无数据区域。勘探人员能够以图中黄色以及红色连片区域作为参考，进行有利区的圈定。

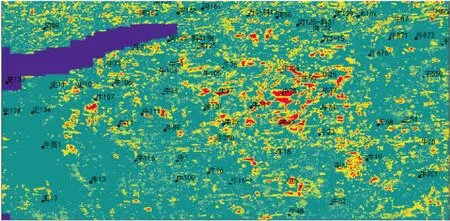
图2 东营某区域有利区预测结果

3 结论和认识

(1) 采用岭回归与逻辑斯谛分类相融合的算法进行有利区预测，分类准确率达到60.0%以上，与常规储层预测方法相比效果明显，证明了该文提出的基于机器学习预测方法的有效性。

(2) 通过预测结果，得到有利区的大概分布范围，为地质勘探人员打井提供了一种参考，从而快速圈定有利区。

(3) 因有利区的判定不仅与地震属性相关，后续研究将综合考虑除地震属性之外的地质构造特征、测井解释成果、试油结论等进行有利区的预测，同时，将会不断实践新的算法以及改进算法，进一步提高利用机器学习预测有利区的准确率。