矩阵模型修正中一类多约束矩阵逼近问题
张 丽,周学林,李姣芬
(1.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004;2.桂林电子科技大学 教务处,广西 桂林 541004)
矩阵模型修正在工程和动力学系统等方面有非常重要的意义。文献[1-2]利用交替投影算法研究矩阵模型修正中如下结构约束矩阵逼近问题:
(1)
其中‖·‖F为常用的矩阵Frobenius范数,y⊂Rn×n为闭凸集合,问题(1)假定线性矩阵方程AXB+C=0是相容的。文献[1-2]只讨论了较简单的相容矩阵方程约束条件AXB+C=0,因交替投影算法需要给出在相容矩阵方程解集合中投影矩阵的具体解析表达式,故该算法并不能把问题模型(1)推广至更一般情形的相容矩阵方程约束条件。为此,利用目前较成熟的交替方向法[3-4],讨论如下具有更一般形式的多约束矩阵逼近问题。
问题1给定矩阵C∈Rm×s,G∈Rn×n和闭凸集合y⊂Rn×n,求X∈Rn×n,使得
(2)
其中A(X):Rn×n→Rm×s表示具有一般形式的线性矩阵方程算子,其转置(伴随)算子记为AT(·):Rm×s→Rn×n。同样假定线性矩阵算子方程A(X)+C=0是相容的。对于闭凸集合y⊂Rn×n的选取,假定y上的投影矩阵Py(·)易求得。较常用的约束集合为对称矩阵集合、Hankle型矩阵集合、非负矩阵集合、对称半正定矩阵集合等。
1交替方向法求解问题(2)
为方便求解,引入辅助变量Y∈Rn×n,将问题(2)转换成如下等价形式:
s.t.X-Y=0,X∈y,Y∈Ω。
(3)
其中Ω={Y∈Rn×n|A(Y)+C=0}为非空的仿射子空间。问题(3)对应的增广拉格朗日函数为

(4)
其中β>0为罚参数,Z∈Rn×n为拉格朗日乘子矩阵。传统的交替最小二乘法用以下迭代格式对式(4)进行极小化求解,
其中(Xk,Yk,Zk)为给定的迭代步。上述求解方法忽略了目标函数的可分离结构特点,因此考虑充分利用其可分离结构特点的交替方向法。先对X求极小化,再对Y求极小化,其迭代式为:
(5)
2 子问题的求解
由式(5)可知,X和Y的子问题可表示为:

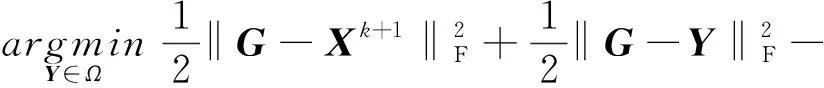
对于X子问题,参照文献[4]的方法可得,

2tr(XT(G+βYk+Zk))+c}⟺

因假定y是具有特殊结构的闭凸集,且易求得任意n×n矩阵在集合y内的投影矩阵,故可得式(5)中X子问题的具体解析表达式,
(6)
对于Y子问题,同样可得
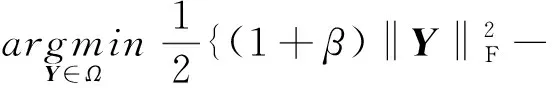
2tr(YT(G-βXk+1+Zk))+c}⟺

(7)
因为假定仿射子空间Ω={Y∈Rn×n|A(Y)+C=0}是非空的,且易知其上的最佳逼近解是唯一的。但由于线性矩阵算子A(Y)的一般性,故Ω上的投影矩阵的具体表达式不易求得,因此迭代式(5)中Y子问题不能求得其解析表达式。为此,从构建内迭代算法的角度求得Y子问题的近似解,即求在非空仿射子空间Ω上最佳逼近问题(7)的近似解。求解思路是将求式(7)的唯一最佳逼近解等价转化为求一个相容线性矩阵算子方程的唯一最小范数解。首先,将式(7)等价转换为
(8)
因为
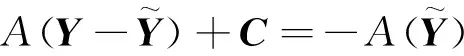
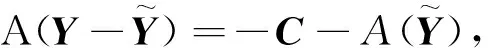
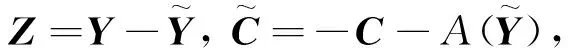
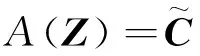
(9)
的唯一的最小范数解。记方程(9)的唯一最小范数解为Z*,最佳逼近问题(8)的唯一解可表示为
对于相容线性矩阵方程的求解或其最小范数解,近年来已有非常丰富的研究成果[5-6]。参照文献[5]的矩阵形式的共轭梯度算法求解相容线性矩阵方程(9),并通过选取特定的初始矩阵得到方程(9)的唯一最小范数解。


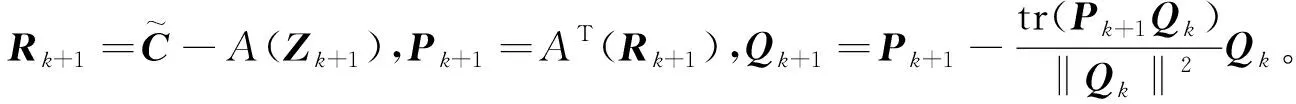
对于算法1,可以证明该算法具有有限步终止特性[5]。
引理1[5]对于相容线性矩阵方程(9),任意给定初始矩阵Z1∈Rn×n,迭代算法1经过有限步迭代可得到方程(9)的一个解。
若取特定的初始矩阵,则由算法1可得到方程(9)的唯一的最小范数解[4]。

由引理2可知,问题(8)的唯一最佳逼近解
(10)
算法2取罚参数β>0,给定当前迭代步(Xk,Yk,Zk)∈(y,Ω,Rn×n),则生成新的更新迭代步(Xk+1,Yk+1,Zk+1)∈(y,Ω,Rn×n):
1)按式(6)生成Xk+1,即

3)更新乘子矩阵Zk+1=Zk-β(Xk+1-Yk+1)。
算法2的终止条件为:
max{‖Xk+1-Xk‖F,‖Yk+1-Yk‖F,
‖Zk+1-Zk‖F}≤ε,
其中ε为给定的正常数。
3 收敛性分析
(11)
将式(11)变分不等式写成一种紧凑形式
V(f,F,M):f(U)-f(U*)+
〈W-W*,F(W*)〉≥0,∀W∈M,
其中
(12)
得到紧形式
f(U)-f(Uk+1)+〈W-Wk+1,F(Wk+1)+
η(Yk,Yk+1)+H0(Vk+1-Vk)〉≥0,
(13)
其中
(14)

引理3在式(12)中定义的映射F(W)满足

定理1由式(2)生成的序列{Xk+1}满足
(15)
证明从H与H0之间的关系可得
(Wk+1-W*)TH0(Xk-Xk+1)=

〈Xk+1-X*,H(Xk-Xk+1)〉,
在式(13)中令W=W*,可得
〈Xk+1-X*,H(Xk-Xk+1)〉≥
〈Wk+1-W*,η(Yk,Yk+1)〉+f(Uk+1)-
f(U*)+〈Wk+1-W*,F(Wk+1)〉≥
〈Wk+1-W*,η(Yk,Yk+1)〉。
(16)
对于鞍点(X*,Y*)有X*-Y*=0,由Zk+1的迭代,得
〈Wk+1-W*,η(Yk,Yk+1)〉=
〈Yk-Yk+1,β{(-Xk+1+Yk+1)+
(X*-Y*)}〉=
〈Yk-Yk+1,-η(Xk+1-Yk+1)〉=
〈Yk-Yk+1,Zk+1-Zk〉,
在式(11)的第2个不等式中令Y=Yk,得到
f2(Yk)-f2(Yk+1)+〈Yk-Yk+1,Zk+1〉≥0,
(17)
即
f2(Y)-f2(Yk)+〈Y-Yk,Zk〉≥0。
令Y=Yk+1,可得
f2(Yk+1)-f2(Yk)+〈Yk+1-Yk,Zk〉≥0,
(18)
式(17)、(18)相加可得,
〈Yk-Yk+1,Zk+1-Zk〉≥0⟹
〈Xk+1-X*,H(Xk-Xk+1)〉≥0。
因此以下不等式成立,
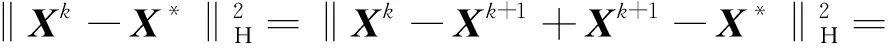
2〈Xk+1-X*,H(Xk-Xk+1)〉≥
4 Nesterov加速策略
文献[7-8]将梯度下降法的Nesterov加速策略应用于交替投影方向法,其核心是引入预估校正型的加速步。文献[6]将Nesterov加速策略应用于求解核范数和谱范数的广义Sylvester方程最小二乘问题,其数值实验部分验证了该加速方案是切实可行的。因此,将带“重启规则”Nesterov加速策略应用于算法2的交替方向法。
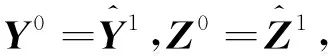

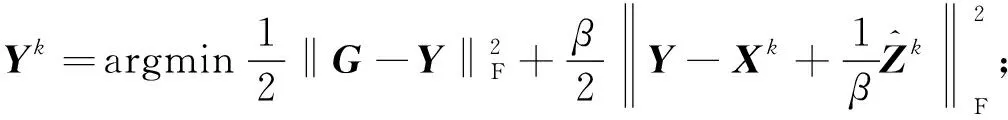

4)若ck<ηck-1,则令
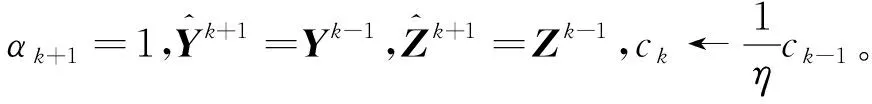
5 结束语
针对矩阵模型修正中一类多约束矩阵逼近问题,利用交替方向法,通过引入辅助变量将问题等价转化为可分离变量的矩阵优化问题,并利用投影和构造内迭代算法,求出子问题的解析表达式,应用相关矩阵理论证明了算法的收敛性定理。对于给出的带“重启规则”的Nesterov加速策略,今后将通过数值实验来研究加速策略的加速效果。

