剪切波对HIFU经颅聚焦形成温度场影响的数值仿真研究

张艳秋 张 浩 孙天宇 菅喜岐

(天津医科大学生物医学工程与技术学院 天津 300070)

0 引言

高强度聚焦超声(High-intensity focused ultrasound,HIFU)是将超声波聚焦在靶区组织上使靶区组织温度升高致死病变组织的治疗技术，具有无创/微创、可重复治疗等优势，现已应用于子宫肌瘤[1]、前列腺癌[2]、乳腺癌[3]、胰腺癌[4]等软组织肿瘤的临床治疗，HIFU经颅治疗胶质瘤[5]、神经刺激[6]、运动障碍[7]脑部神经系统疾病也进入临床试验。经颅HIFU治疗的挑战是颅骨引起的超声急剧衰减、颅骨与周围软组织阻抗差异大而引起的焦点失真、移位。2001年，Clement等[8]利用凹平面单阵元换能器对经颅超声传播路径进行了数值仿真和离体人体颅骨实验验证，结果表明当超声波入射角度大于20◦时，HIFU经颅治疗中剪切波的影响不可忽略。2004年，Concor等[9]利用开口直径为300 mm的500阵元的半球状相控换能器进行经颅聚焦，数值仿真结果表明，在未考虑剪切波条件下，大口径半球形换能器可避免颅骨及其周边组织损伤，并在颅内形成可治疗焦域。2006年，White等[10]利用开口直径为12.7 mm的单阵元换能器辐照人离体颅骨，通过垂直入射法测得纵波经颅传播速度，测定结果表明，当入射角度大于40◦时，超声波传播速度大于已测得的纵波传播速度，剪切波的传播可以提高能量传输效率。2011年，Pinton等[11]利用开口直径为300 mm的512阵元相控换能器对HIFU经颅形成的温度场进行了仿真研究，结果表明，在相同焦距条件下，颅内浅表组织内形成的可治疗焦域体积小于深层组织。2015年，Jones等[12]利用开口直径为300 mm的128阵元稀疏分布半球形相控换能器进行经颅聚焦，并基于CT进行像差校正，结果表明，在未考虑剪切波条件下，基于人颅骨CT的异质颅骨模型的像差校正优于均质颅骨模型。2015年，Ding等[13]在未考虑剪切波影响的条件下进行了HIFU经颅声压场和温度场的数值仿真研究，研究结果表明，采用时间反转法结合振幅调制相控，可以降低颅骨处的温升。2018年，王祥达等[14]利用256阵元平面相控阵结合猴颅骨CT建立了经颅聚焦的数值仿真模型，结果表明，考虑剪切波的数值仿真模型形成焦域处声强更大，当聚焦深度较大时可以不考虑剪切波。

本文建立由曲率半径为150 mm的半球形相控换能器和人体头颅CT数据构成的三维数值仿真模型，并利用时域有限差分法(Finite difference time domain,FDTD)结合Westervelt声波非线性传播方程、动量方程、运动守恒方程和Pennes生物热传导方程进行声压场和温度场的数值仿真。分析研究不同聚焦角度、不同阵元数和相同输入功率条件下剪切波对形成焦域面积的影响，为HIFU经颅治疗方案制定提供理论依据。

1 基本方程式

1.1 声压场

1.1.1 脑组织和水内声压场

在水、人体软组织和不考虑剪切波影响的骨组织内，采用Westervelt声波非线性传播方程[15]：

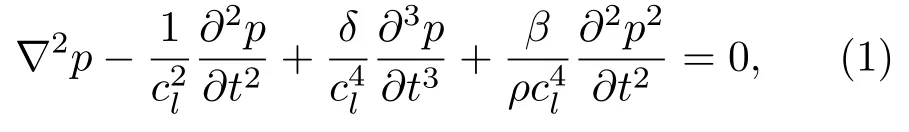
式(1)中：∇为拉普拉斯算子；p为声压；cl和ρ分别为纵波声速和密度；β=1+B/(2A)为非线性系数，B/A为介质的非线性参数；t为时间；扩散系数δ为

式(2)中：α为吸收系数，ω=2πf为角频率，f为频率。

1.1.2 骨组织内声压场

动量方程和质量守恒方程适用于含水70%的人体组织内的声波传播[16]。对于骨组织超声波传播可在质量守恒方程中加考虑剪切波的弹性项来实现[17]。未考虑骨黏度时骨组织内声波传播的动量方程和质量守恒方程[18]：

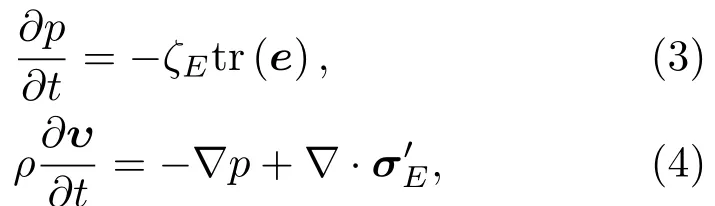
其中：υ为纵波传播速度矢量；体积模量ζE=其中，剪切模量为剪切波传播速度；弹性应力张量为

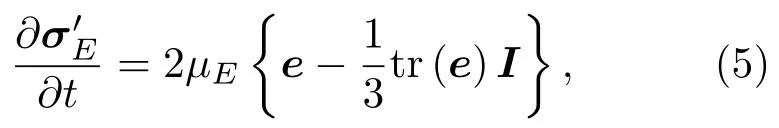
式(5)中：I为单位张量；形变张量e为

1.2 温度场

Pennes生物体组织内热传导方程[19]为

式(7)中：Cr为比热；T为温度；rec为热传导率；q为单位体积发热量；WB为血流灌注率；CB为血流比热。

2 数值仿真模型及仿真参数

图1为利用46岁男性健康志愿者人体头颅CT数据和开口直径为300 mm的256阵元半球形随机分布相控换能器建立的经颅辐照数值仿真模型。其中，换能器的随机分布阵列在相邻阵元间距不小于1.0 mm的条件下依次选定各阵元中心位置，阵元半径为8.5 mm。聚焦深度为45 mm，数值仿真区域大小为200 mm×300 mm×300 mm，声轴为z轴。数值仿真的空间步长dx=dy=dz=0.3 mm，数值仿真的时间步长dt=10 ns，模型边界采用Mur一阶边界吸收条件进行处理。水体、颅骨和脑组织各仿真参数[18,20]如表1所示。根据不同的聚焦角度θ在换能器基底选取部分阵元进行激励，总功率为150 W时，阵元激励参数如表2所示。

图1 256阵元半球形随机分布相控换能器经颅辐照数值仿真模型(单位：mm)Fig.1 Numerical simulation model of transcranial irradiation of 256 elements hemispherical randomly distributed phase controlled transducer(Unit:mm)

表1 水体、颅骨和脑组织仿真参数Table 1 Water,skull and brain tissue simulation parameters

表2 阵元激励参数Table 2 Array element excitation parameters

3 结果

以图1所示数值仿真模型，利用时间反转法获取阵元激励信号，结合相位调控和幅值补偿进行经颅辐照，输入总功率为150 W，阵元激励频率选用0.7 MHz。

3.1 剪切波的影响

图2 不同聚焦角度换能器在几何焦点处聚焦的焦平面温度场Fig.2 Focal plane temperature field with different focus angle transducers focused at geometric focus

不同聚焦角度换能器在形成焦域的最大温度达到65◦C时的温度场如图2所示。由图2可知，随换能器聚焦角度θ减小，在几何焦点处形成的焦域面积逐渐增大，达到65◦C所需时间逐渐延长；当聚焦角度60◦6θ6 150◦考虑剪切波的影响时，相同的聚焦角度条件下，温度场达到65◦C所需时间tmax更短，旁瓣更少，颅骨处温升不明显；当聚焦角度θ=30◦时，考虑剪切波的温度场与未考虑剪切波的温度场达到相同温度所需时间相同；当聚焦角度θ<90◦时，焦点前移且在颅骨处产生较高温度；当聚焦角度θ=30◦时，颅骨处温升较大。图3为与图2对应的声轴温度曲线。由图3可知，在相同聚焦角度下，考虑剪切波形成的温度场在颅骨处的温度更高。图4为与图2对应的不同聚焦角度下焦平面面积和辐照时间。由图4可知，随着聚焦角度的增大，考虑剪切波形成的焦域面积小于未考虑剪切波形成的焦域面积。图5为与图2对应的不同聚焦角度换能器形成的焦域最高温度与预设焦点在声轴上的偏离距离。由图5可知，聚焦角度减小，考虑剪切波与未考虑剪切波形成最高温度在声轴上的偏离增大，当聚焦角度θ>90◦时，两者间几乎无差异。

图3 不同聚焦角度换能器在几何焦点处聚焦的声轴温度曲线Fig.3 Sound axis temperature curve of different focus angle transducers focused at geometric focus

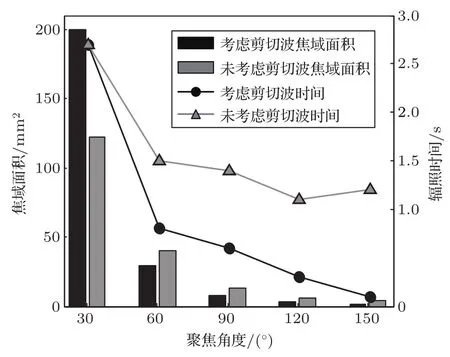
图4 不同聚焦角度换能器在几何焦点处聚焦的焦平面面积柱状图和辐照时间折线图Fig.4 Focal plane area histogram and irradiation time line graph of different focus angle transducers focused at geometric focus

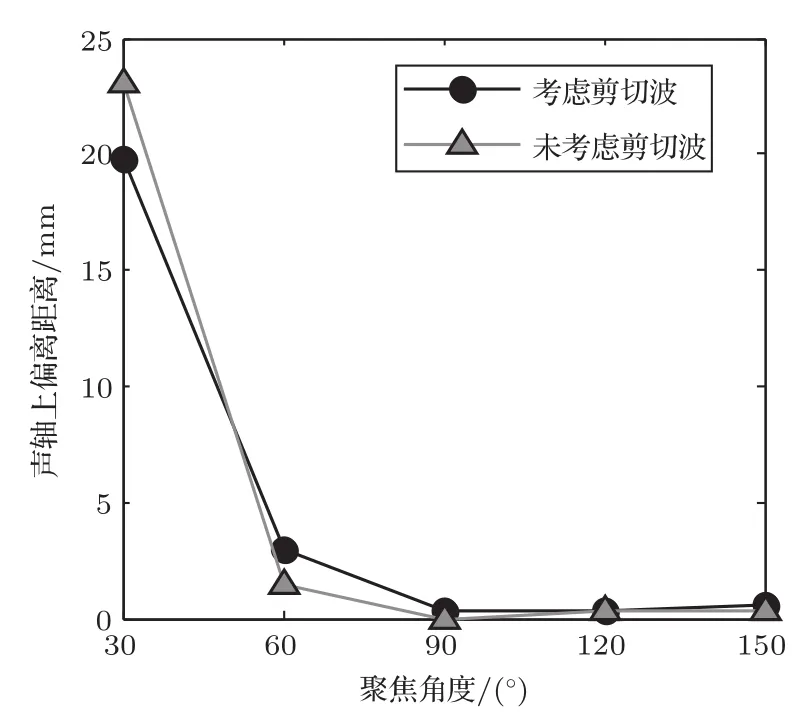
图5 不同聚焦角度换能器形成的焦域与预设焦域在z轴上的偏离距离Fig.5 Deviation distance between the focal region formed by the transducers with different focus angles and the preset focal region on the z-axis

3.2 聚焦角度与焦域面积的相关性

基于图4的数值仿真数据，利用幂指数函数形式，在Matlab平台上得到的拟合式为

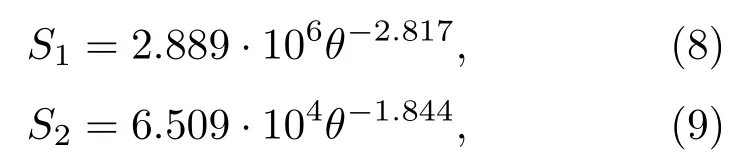
其中：S1为考虑剪切波的焦域面积，S2为未考虑剪切波时的焦域面积。

图6为基于图4的焦域面积的仿真值拟合曲线。由图6可知，考虑剪切波的拟合值与仿真值之间的和方差为3.215，均方根为0.8965，可决系数为0.9999；未考虑剪切波的拟合值与仿真值之间的和方差为64.01，均方根为4，可决系数为0.9941。考虑剪切波情况下，焦域面积的拟合值与仿真值之间的和方差更小，均方根更接近于0，确定系数更接近于1。

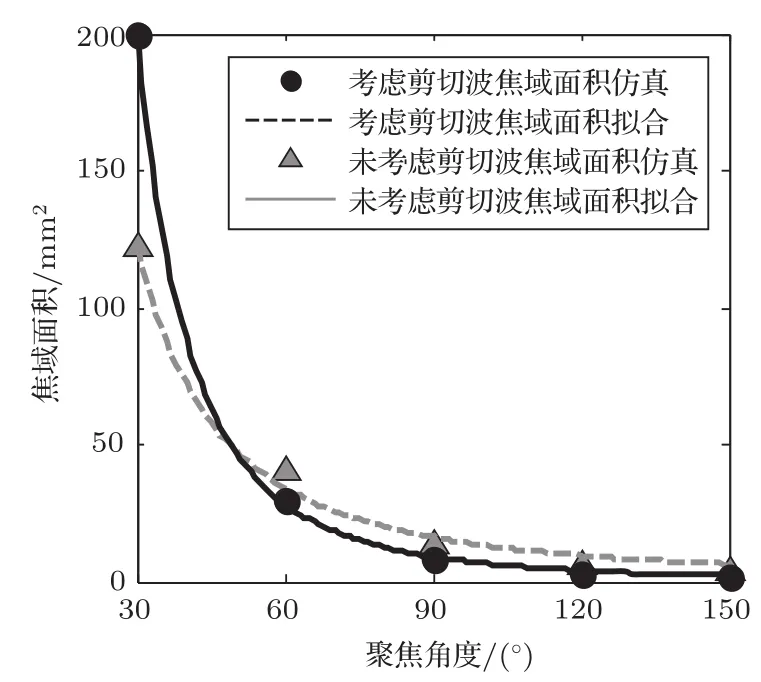
图6 不同聚焦角度换能器在几何焦点处聚焦形成的焦域面积拟合曲线Fig.6 Focal domain area fitting curve formed by different focus angle transducers at geometric focus

4 结论

本文基于半球形相控换能器经颅辐照模型，建立了未考虑剪切波传播和考虑剪切波传播的两种经颅辐照的数值仿真模型，并对激励不同聚焦角度阵元的情况下形成的温度场进行研究，得到以下结果：

(1)随换能器聚焦角度θ减小，在几何焦点处形成的焦域面积逐渐增大，焦点前移程度越大，考虑剪切波形成的温度场达到65◦C所需时间逐渐延长。

(2)在相同聚焦角度条件下，考虑剪切波的温度场达65◦C所需时间更短，旁瓣更少。

(3)随换能器聚焦角度θ减小，考虑剪切波的模型形成的焦域面积变化范围更大。

(4)经颅考虑剪切波情况下，焦域面积的仿真值与拟合值之间的和方差更小，均方根更接近于0，确定系数更接近于1。

由上述结果得到如下结论：

(1)在输入功率和焦域最高温度相同的条件下，聚焦角度越小的换能器形成焦域越大，焦点前移距离越大。

(2)考虑剪切波的传播可以提高能量传输效率，但对焦点前移几乎没有影响。

(3)剪切波在颅骨处传播会导致颅骨内热沉积相对增多。

(4)幂指数函数形式拟合优度高，可预测不同聚焦角度换能器形成的焦域面积。

综上所述，考虑剪切波的温度场的温升速度更快，形成焦域面积更小且旁瓣数量更少，但颅骨处热沉积更多。对于不同患者以及同一患者不同位置上的肿瘤治疗时，应根据肿瘤位置与相控换能器之间的相对位置以及肿瘤大小等，考虑剪切波对形成焦域的影响，以保障HIFU脑肿瘤治疗的有效性和安全性。

5 讨论

将图1中的半球形换能器和头颅结构细化为图7所示x-z与y-z平面图，设定顶骨部分为同心圆弧。聚焦角度θ在30◦∼150◦之间时，最大入射角度λmax为8◦∼30◦，随聚焦角度增大，最大入射角度增大，颅骨处相对温升减小且旁瓣减少。这与2013年Narumi等[21]通过改变超声波从水中入射丙烯酸板的入射角度，提出的超声波入射角度在0∼34.3◦时，随超声入射角度增大，剪切波透射率增加的结论一致。

(1)图1所示的9∼193阵元相控换能器数值仿真模型中，当聚焦角度为60◦∼90◦时，超声最大入射角度为8◦∼20◦之间，剪切波对形成温度场的影响不可忽略，这与文献[8]的单阵元换能器进行经颅辐照所得结果不一致。

(2)本文基于人体真实颅骨CT和256阵元半球形相控换能器，在最大入射角度为8◦∼30◦范围内进行了研究，其研究结果与文献[14]结果相一致。

(3)本文利用最小二乘法对不同聚焦角度换能器经颅聚焦形成焦域面积进行拟合时，出现与实际不符的负数；选用反比例函数和幂指数函数法进行拟合时，幂指数函数形式拟合精度更高。

(4)本研究采用一名志愿者头部CT数据建立三维数值仿真模型，研究了剪切波对HIFU经颅聚焦形成温度场影响。而不同患者的颅骨厚度、密度、曲率的差异很大，为了研究不同患者之间的差异性，下一步将导入多位志愿者的头颅CT数据进行相关数值仿真模型，通过统计的方法研究颅骨厚度、密度、曲率等对剪切波传播的影响。

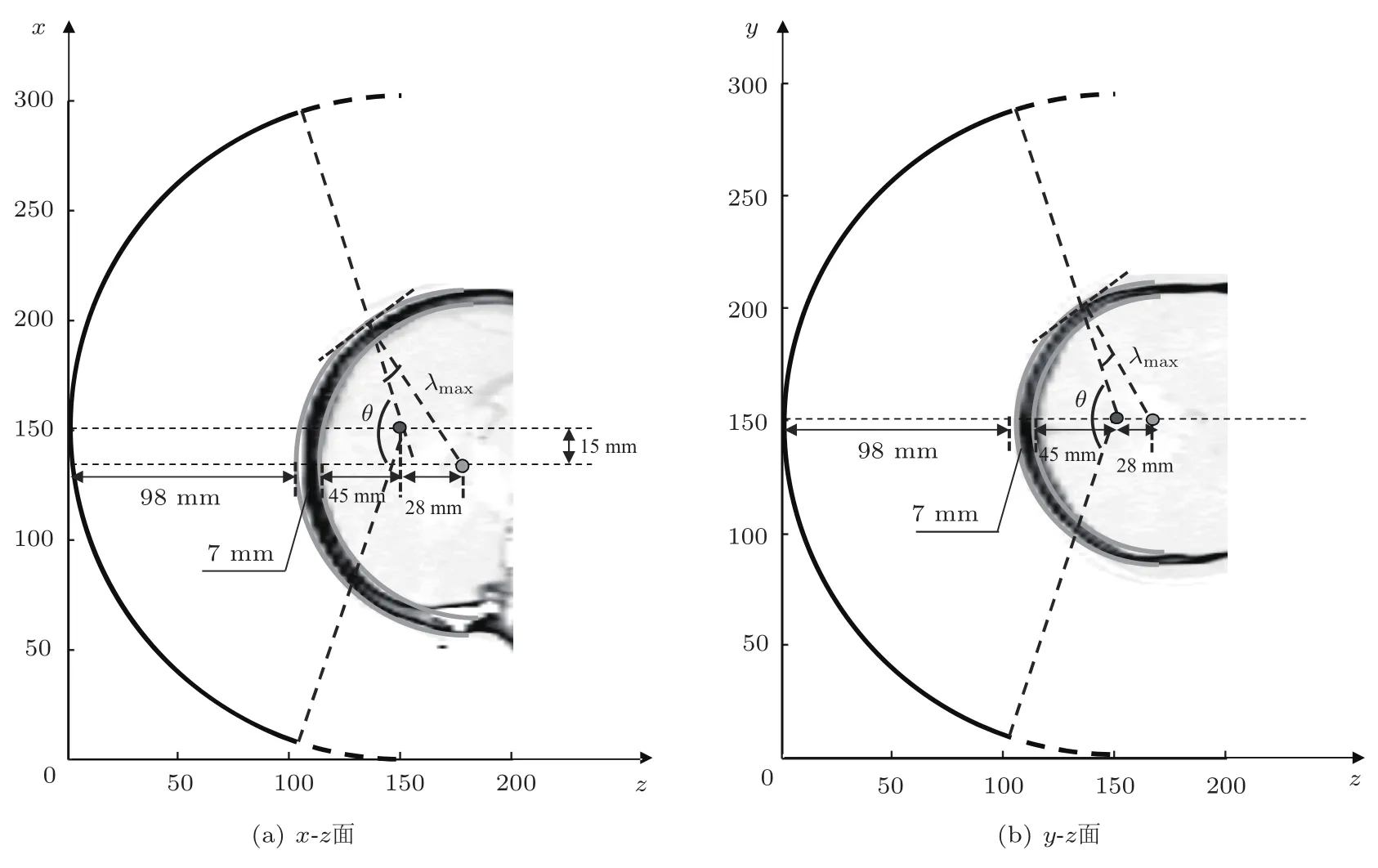
图7 超声最大入射角度计算示意图Fig.7 Schematic diagram of the maximum incident angle of ultrasound