MATLAB在《数值分析》课程中的教学研究——插值方法及其应用分析

靳海娟

（长治学院 数学系，山西 长治 046011）

1 前言

《数值分析》（Numerical Analysis）是大学数学教学的必修课程。为了达到理想的教学效果，借助MATLAB软件以实验课的形式辅助教学越来越常见。MATLAB是目前世界上最为通用的数学和工程计算软件之一，尤其是在《数值分析》课程的算法实现方面，发挥着巨大的作用。

2 基于MATLAB软件的插值方法

2.1 插值法的基本概念

x0，x1，x2，…，xn为[a，b]上 n+1个互不相同的点，f（x）为定义在区间[a，b]上的函数，准为给定的一个函数类，若准上有函数φ（x），满足

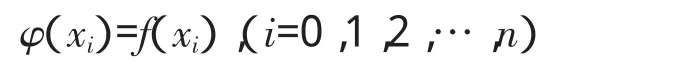
则称 x0，x1，x2，…，xn为插值节点，φ（x）为插值函数，f（x）为被插函数，这种求函数近似式的方法称为插值法[6]。

2.2 多项式插值

2.2.1 Lagrange插值法

先构造 Lagrange插值基函数 li（x）（i=0，1，2，…，n），它的次数不超过n，且满足

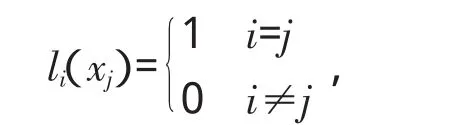
然后以对应点处的函数值为系数作线性组合，即得所要求的多项式，由多项式li（x）有n个根xj（j=0，1，…，i-1，i+1，…，n）故它必有如下形式：

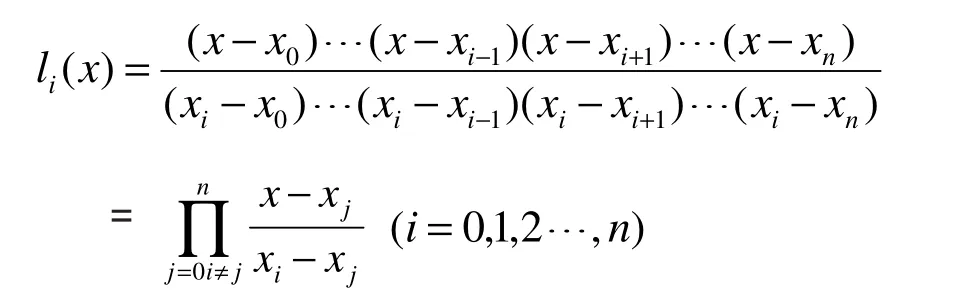
n次Lagrange插值多项式的Ln（x）的公式为：

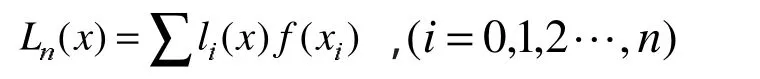
余项为

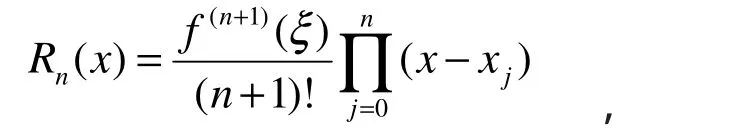
ξ 介于 x与节点 x0，x1，…，xn之间。

2.2.2 牛顿插值法

设有函数f（x），x0，x1，x2，…，xn为一系列互不相等的点，

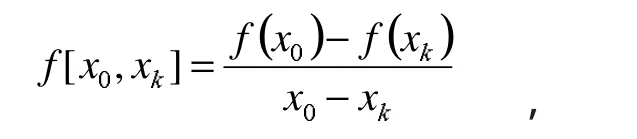
k=1，2，…，n为f（x）关于节点x0，xk的1阶差商，

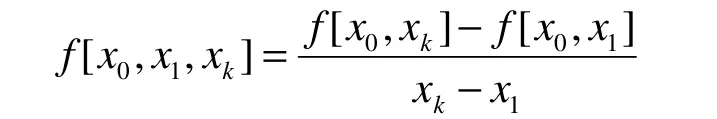
（k=1，2，…，n）为f（x）关于节点x0，x1，xk的二阶差商。

一般的若定义了k-1阶差商，则称

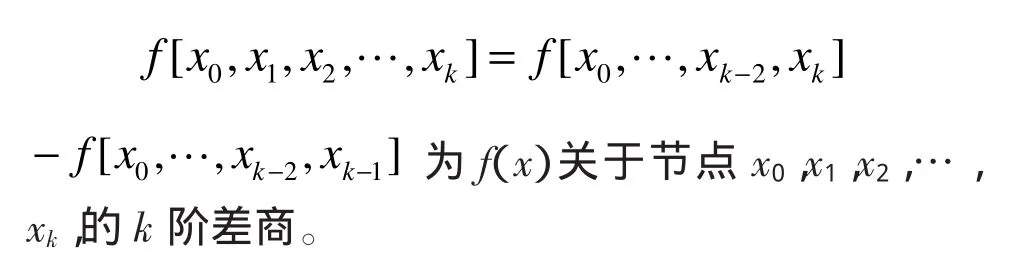
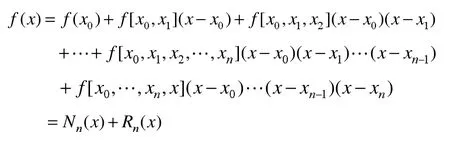
其中Newton插值公式为：

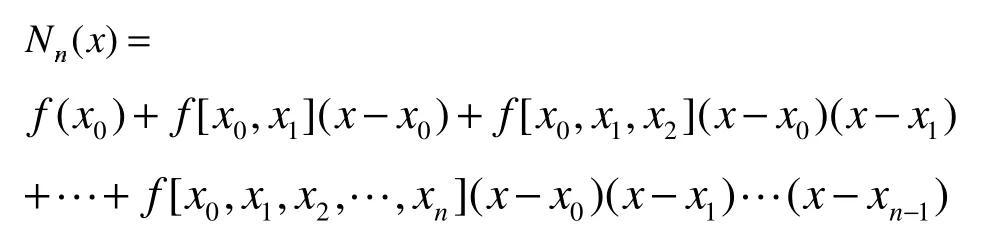
注意：由插值多项式的唯一性定理可知，Nn（x）=Ln（x）为f（x）关于节点x0，x1，x2，…，xn的Lagrange插值多项式。

2.2.3 分段线性插值法

分析插值结果可以发现，实线为原函数f（x），在[-5，-4]和[4，5]部分，L10（x）比L5（x）效果更差，这种高阶插值的振荡现象称为Runge现象。避免高阶插值Runge现象的基本有效方法是使用分段函数进行分段插值。

对给定的区间[a，b]作分割（一般选择等分）：a=x0＜x1＜x2＜…＜xn=b 在每个小区间 [xi，xi+1]上作f（x）以xi，xi+1为节点的线性插值，记这个线性插值函数为si（x），则

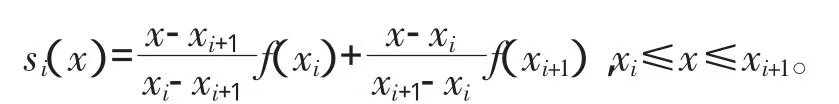
于是就得到了分段线性插值函数。记为P（x），P（x）有如下特点：

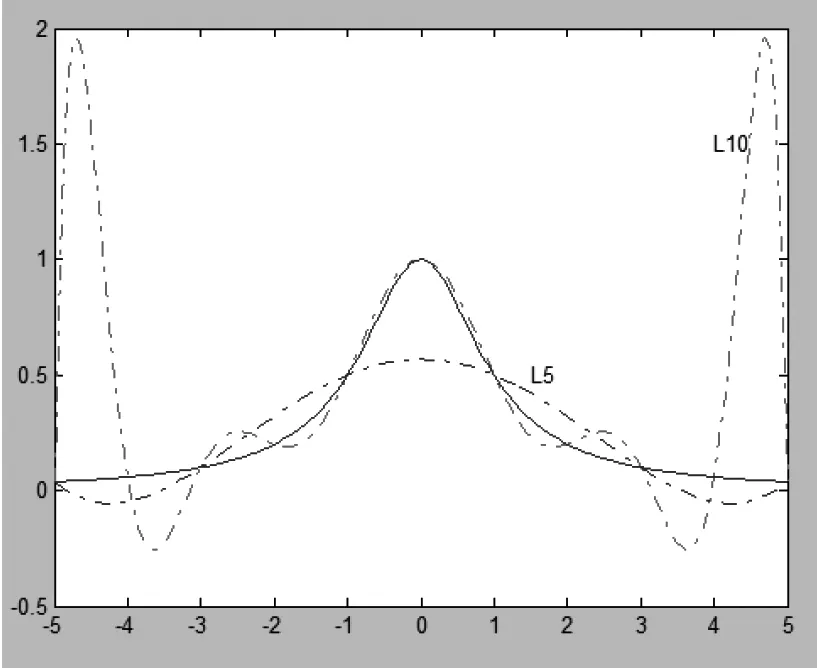
图1 高阶插值的Runge现象

P（x）∈C[a，b]。

P（x）在[xi，xi+1]上为一个不高于一次的多项式。

2.3 插值法的应用分析

在渔业评估的问题中，往往要求解体长与体重的关系。下面我们分别运用Lagrange插值法，Newton插值法和分段线性插值法对该问题进行分析研究。基本思想如下：

把测量次数确定为j=0，1，…，n时，测量同一种不同大小的鱼类样品对应的体长与体重数据（xj，yj），其中xj表示第j条鱼的体长，yj表示第j条鱼的体重，即求n次多项式Pn（x），使满足条件：

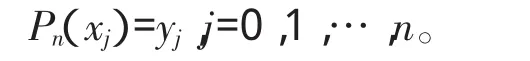
xj为插值节点。已知一组鱼体长与体重的实测结果如下表1所示。

表1 北部湾蓝圆鳝体长和体重的的实测结果

取四个节点 x0，x1，x2，x3。分别用 Lagrange插值，Newton插值，分段线性插值法进行插值，构造3阶插值多项式与原函数进行比较，分析各个插值多项式与原函数的接近程度。

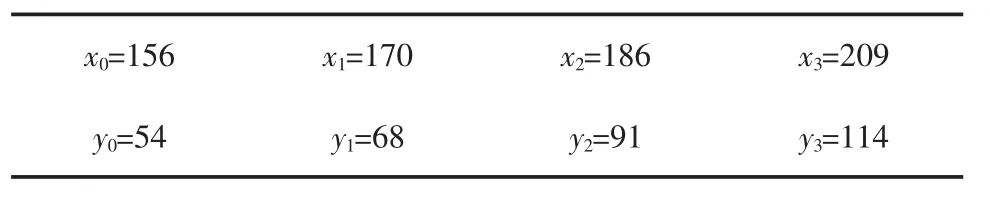
表2 节点表

由此可得Lagrange插值多项式：

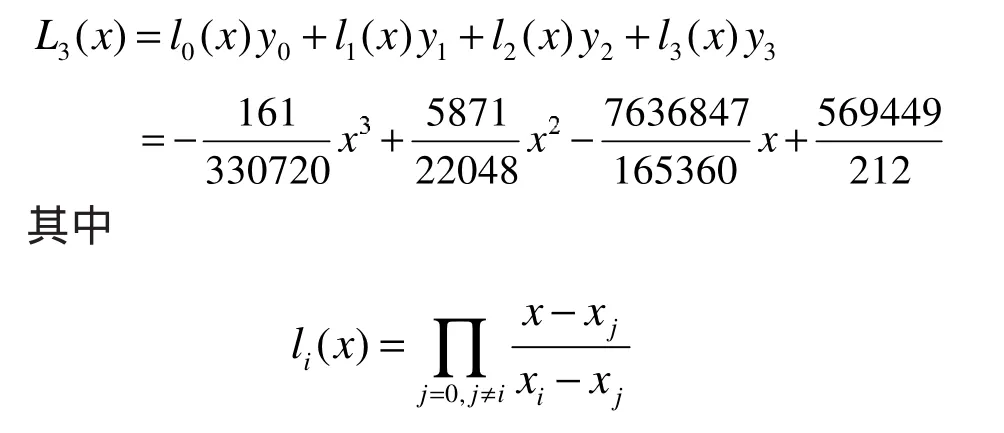
Newton插值多项式：

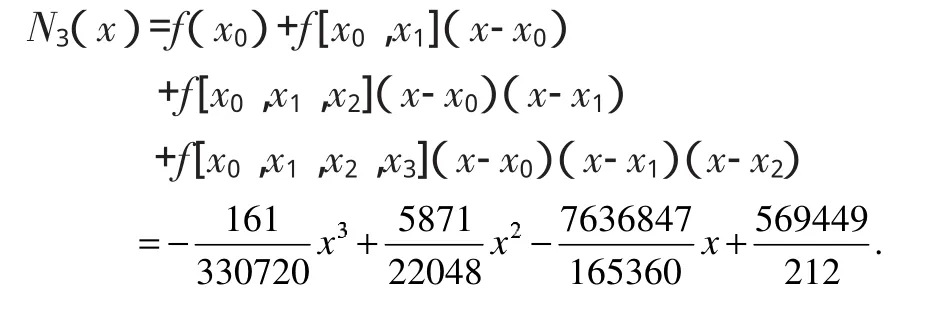
其中

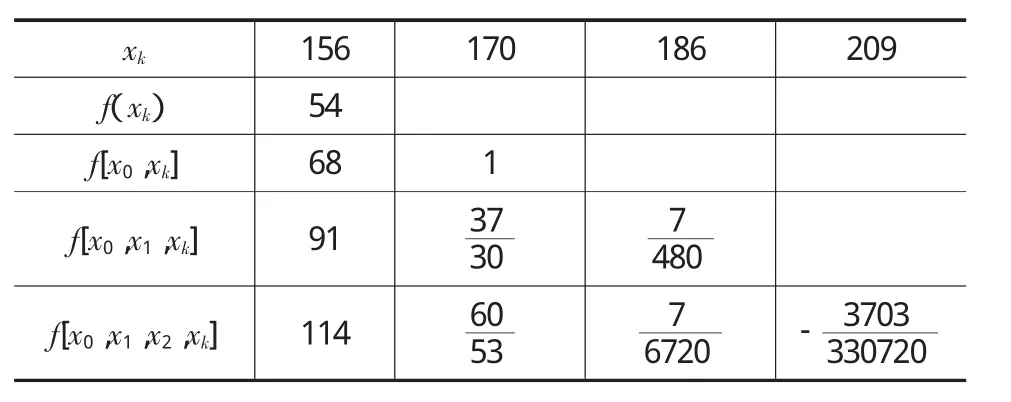
表3 3阶差商

由L3（x）与N3（x）的计算结果可知L3（x）=N3（x），也正验证了插值多项式的唯一性这一结论。下面用MATLAB作图比较Lagrange插值多项式与原函数的接近程度，进而分析Lagrange插值法的插值效果，结果如图3所示。

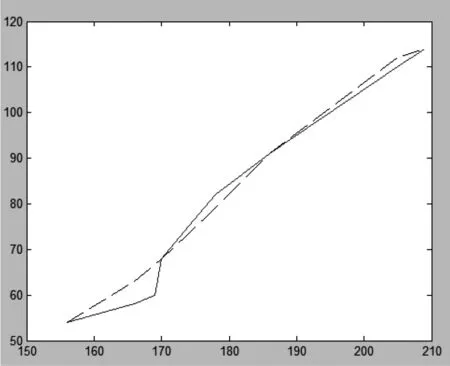
图2 Lagrange插值与原函数图像比较

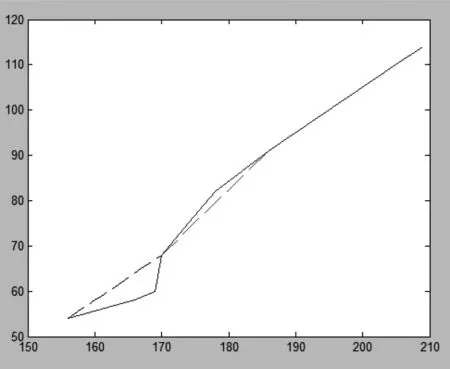
图3 分段线性插值与原函数作图比较

由运行结果可知，实线为原函数f（x），虚线为Lagrange插值多项式L3（x）或Newton插值多项式N3（x）。分析插值结果可以发现，Lagrange插值法的插值效果符合要求。

（3）分3段线性插值多项式

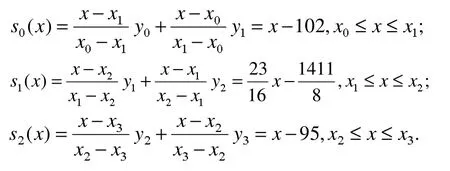
下面用MATLAB作图比较分段线性插值多项式与原函数的接近程度，进而分析分段线性插值法的插值效果。

由图2，图3可知，实线为f（x），虚线为P（x），且分段线性插值多项式P（x）的S2（x）与原函数完全重合，从图2和图3对比可以看出：用分段线性插值法比Lagrange插值法更接近原函数。

则有以下结论：已知鱼的体长估测其体重时，运用Lagrange插值法和Newton插值法结果是相同的，但从其多项式表达式上讲，Newton插值要比Lagrange插值简单。在运用Lagrange插值法时，要注意插值节点个数的选择，当节点选择过多时，高次多项式虽然是连续的，但是很多情况下不一定收敛，甚至可能会产生Runge现象。而分段线性插值则因为在每一小区间上都是线性插值，从而极大地降低了插值多项式的次数，克服了Lagrange值法当节点不断加密时出现的Runge现象。它的缺点是所求的插值函数的光滑性较差，这就要求一种更好的方法来克服这一缺点。