灰色关联及非线性规划法构建传递函数估算黑土水力参数

王子龙，常广义，姜秋香，付 强，陈伟杰，林百健，印玉明

灰色关联及非线性规划法构建传递函数估算黑土水力参数

王子龙，常广义，姜秋香※，付 强，陈伟杰，林百健，印玉明

（东北农业大学水利与土木工程学院，哈尔滨 150030）

土壤水分特征曲线和饱和导水率是重要的水力参数，为了简便准确获取这些参数，以松嫩平原黑土区南部为研究区域，采集136个采样点土样用于测定不同土层土壤水分特征曲线、饱和导水率以及土壤理化性质，并运用灰色关联分析确定影响土壤水力参数的主要土壤理化性质，采用非线性规划构建土壤分形维数、有机质、干容重、土壤颗粒组成与土壤水分特征曲线、饱和导水率之间的土壤传递函数，并通过与现有土壤传递函数对比分析进行精度验证。结果表明：1）土壤分形维数是估算土壤水分特征曲线模型参数和饱和导水率的主要参数之一，同时，干容重和有机质含量也在不同土层土壤传递函数中起到重要的作用；2）通过验证分析，不同土层各参数平均绝对误差接近于0，均方根误差值也都较小，其中在不同土层土壤传递函数估算的土壤含水率均方根误差分别为0.022、0.017 cm3/cm3；3）对比分析其他已存的土壤水分特征曲线和饱和导水率的土壤传递函数，该文构建的土壤传递函数均方根误差值均较小，决定系数值都在0.66以上，表明估算精度较高，均好于其他方法估算精度，具有良好的区域适应性。综上，所构建的土壤水分特征曲线和饱和导水率土壤传递函数可以用于松嫩平原黑土区土壤水力参数估算。

土壤；灰色关联；水分；松嫩平原黑土区；土壤水分特征曲线；饱和导水率；土壤传递函数

0 引 言

土壤水分特征曲线和饱和导水率是构建土壤水分与溶质运移模型的重要参数[1-2]。两者都受土壤质地、容重、有机质含量、孔隙度等的影响，不同地区影响因素也存在明显的差异，另外，土壤具有空间变异性特点，随着尺度的变化，各因素的影响强度也随之发生变化[3-4]。直接测定土壤水分特征曲线和饱和导水率具有耗费人力、花费时间、成本高等特点，对于小尺度可行，但对大尺度而言，往往需要采集大量的样本，因此，可操作性较低[5]。

研究表明，通过较为容易测定的土壤基本理化性质来获得土壤水力参数的方法是一种较为简便有效方法，即土壤传递函数。构建土壤传递函数的方法有多元线性和非线性回归、人工神经网络、数据分类分组等方法[6-8]。近年来，国内外学者针对不同地区建立了土壤水分特征曲线、饱和导水率的土壤传递函数。Li等[9]建立了封丘地区土壤水分特征曲线的土壤传递函数，并用于玉米、小麦产量估算，与Vereecken等[10-12]建立的土壤水分特征曲线的土壤传递函数对比分析，结果表明Li等建立的各参数传递函数估算精度最好。孙美等[13]建立了北京大兴区土壤饱和导水率传递函数。孙丽等[14]建立了科尔沁沙丘-草甸相间地区表土饱和导水率的土壤传递函数，并与Wosten等[12,15-17]建立的饱和导水率土壤传递函数对比发现，建立的土壤传递函数估算精度优于Campbell等建立的模型。由此可知，土壤传递函数具有区域局限性的特点，因此，针对研究区域建立一套适应性和精度高的土壤水力性质的传递函数是十分有必要的。

本文以松嫩平原黑土区南部为研究区域，把分形维数引入土壤传递函数当中，采用灰色关联度分析和非线性规划相结合的方法，建立适合松嫩平原黑土区的土壤水分特征曲线和饱和导水率的土壤传递函数，为研究区土壤水分和溶质运移提供参数，同时为区域土壤水力性质的获取提供技术支持。

1 材料与方法

1.1 研究区概况

研究区为松嫩平原黑土区南部的哈尔滨市区、五常市、双城区、阿城区、宾县、呼兰区、巴彦县，如图1所示，总面积达2.8´104km2，约占松嫩平原黑土区面积的20%。研究区属于温带大陆性气候，降水主要集中在 6－9月，主要以水稻、玉米、大豆农作物为主，土壤肥沃，适合农作物生长。

图1 研究区地理位置及采样点分布

1.2 土壤样品的采集与测定

土样的采集时间为2017年7－9月，在农作物未收割之前。采样方案的设计是在综合考虑有机质含量、土壤质地、土壤容重、土地利用、坡度等土壤水力参数重要影响因素的基础上，利用相关分析确定关键影响因子，通过各因子贡献赋值及加权叠加获得空间计算单元的优先级指数和排序，运用合理采样数方法计算采样数量，结合优先级排序确定采样点的空间位置[18]。采样点的布设如图1所示，研究区总共136个采样点，每个采样点分别利用环刀在0～20 cm和>20～40 cm取原状土、自封袋取散土，每个采样点上下2层各取3个重复。原状土用于测定土壤水分特征曲线和土壤干容重。土壤水分特征曲线采用日本HITACHI公司的高速离心机测定在1、3、5、10、30、50、100、300、400、500、700、900 kPa下的体积含水率；饱和导水率（K）采用定水头法测定；土壤干容重（bulk density，BD）采用环刀法测定；散土土样进行风干、过2 mm筛之后，采用英国马尔文仪器公司MS2000激光粒度仪进行土壤颗粒分析，按国际制进行分类，分为砂粒（sand）（粒径≥0.02～2 mm）、粉粒（silt）（粒径≥0.002～0.02 mm）和黏粒（clay）（粒径<0.002 mm）。分形维数（）采用王国梁等[19]提出的方法计算。土壤有机质（soil organic matter，SOM）采用农业行业标准（NY/T1121.6-2006）[20]方法进行测定。

1.3 研究方法

1.3.1 土壤水分特征曲线模型

土壤水分特征曲线的经验模型较多，国内外学者研究表明van Genuchten模型对不同质地的土壤适应程度较高[21-23]，因此本文选择van Genuchten模型来拟合实测土壤水分特征曲线[24]，公式如下：

式中为土壤体积含水率，cm3/cm3；土壤饱和含水率，cm3/cm3；为土壤残余含水率，cm3/cm3；为土壤吸力，cm；=1-1/为模型参数，其中数值上等于土壤进气值的倒数。

1.3.2 土壤传递函数构建方法

目前，为了获得土壤传递函数的具体表达式，以便于推广应用，运用线性回归、非线性回归等统计方法建立的土壤传递函数较多，但是，这些方法构建的土壤传递函数普遍存在极值点处估算值与实测值严重偏差，导致较大计算误差的问题，而非线性规划逐渐逼近目标函数的极值点，能够有效消除极值偏差问题。

本文把灰色关联度分析法（grey relation analysis，GRA）与非线性规划（nonlinear programming，NP）[25-26]相结合构建研究区土壤水力参数传递函数，首先运用灰色关联分析土壤水力参数与土壤理化性质之间的关系，确定对土壤水力参数主要的影响因子，然后采用非线性规划构建van Genuchten模型参数、、和饱和导水率K与土壤分形维数、有机质含量、干容重、土壤颗粒组成之间的土壤传递函数。同时，在0～20 cm和>20～40 cm土层各136个土样中各随机选取109个土样参与土壤传递函数构建，剩余27个土样用于土壤传递函数的精度 验证。

1.3.3 模型精度评价指标

选择平均绝对误差（mean absolute error，MAE）、均方根误差（root of mean square error，RMSE）、决定系数2[9]，对构建的土壤传递函数精度进行评价。

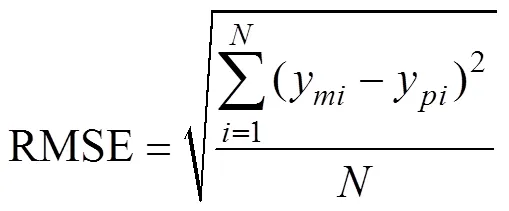
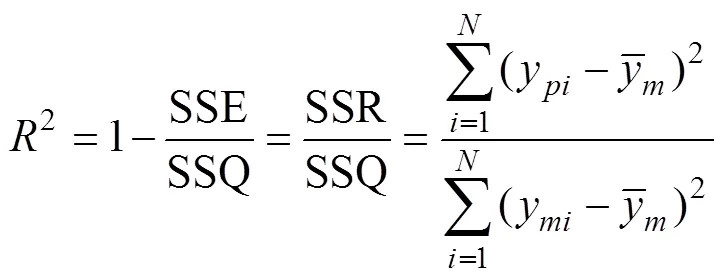
2 结果与分析

2.1 土壤理化特性的统计分析

对研究区土壤理化特性进行统计分析，结果如表1所示。由表可知，研究区0～20 cm土壤中黏粒、粉粒、砂粒体积分数变化范围分别为11.30%～42.95%、11.65%～48.59%、18.13%～76.18%；>20～40cm土壤中黏粒、粉粒、砂粒的体积分数变化范围分别为5.49%～48.95%、3.70%～43%、18.61%～90.80%，由国际制土壤质地分类标准可知研究区土壤质地以壤黏土和壤土为主，其中0～20和>20～40 cm的黏粒、粉粒、砂粒体积含量均属于中等变异，随着土壤深度的增加，土壤黏粒、粉粒、砂粒变异系数均增加。0～20 cm土壤有机质质量分数在4.74%～98.70%范围内，变异系数为41%；而>20～40 cm的则在6.19%～107%之间，变异系数为55%，表明随着土壤深度的增加变异强度增加。0～20 和>20～40 cm土壤干容重均值分别为1.43和1.33 g/cm3，变异程度均为中等变异。另外分形维数在0～20 cm的均值为2.82，在>20～40 cm的均值为2.80，变异系数均为2%，为弱变异。

由表1可知，0～20 和>20～40 cm土层值变化幅度较小；同时，0～20 和>20～40 cm土层参数值比较接近，根据国际制土壤质地分类标准可知研究区2个深度土层土壤质地为黏壤土，土壤质地相似。由0～20和>20～40 cm土层参数值可知，其中<0.1情况占95%以上，表明研究区土壤平均孔径较小、质地较细，属于壤黏土和壤土范畴。

2.2 构建模型估算van Genuchten模型参数及饱和导水率

采用灰色关联法[28]将不同深度土层实测土壤理化指标与不同深度土层土壤水分特征曲线模型参数、、进行定量分析，并对关联度进行排序，如表2所示。关联度大小表示比较序列与参考序列密切程度，关联度越大则两者变化趋势越接近，反之，则越远离。从表2可以看出，随着土壤深度的增加，土壤水分特征曲线模型参数与各指标之间的关联度大小也在发生变化。在0～20 cm土层参数与分形维数关联度最大，与砂粒含量关联度最小；在>20～40 cm土层参数与砂粒含量关联度最大，与粉粒含量关联度最小。在0～20 cm土层参数与分形维数关联度最大，与有机质含量关联度最小；而在>20～40 cm土层参数与分形维数关系最为密切。另外，在0～20 cm土层参数与砂粒含量关联度最大；在>20～40 cm与砂粒含量关联度最大，与黏粒含量关联度最小。

表1 土壤理化特性统计分析

注：样本数为136，变异系数CV>100%时为强变异，10%≤CV≤100%时为中等变异，CV<10%时为弱变异[27]。

Note: Number of samples is 136, Coefficient of variable CV>100% is a strong variation, 10%≤CV≤100% is a medium variation; CV<10% is a weak variation[27].

表2 不同土层van Genuchten模型参数和饱和导水率与土壤理化特性间的灰色关联度和排序

注：K为饱和导水率。

可知研究区PTFs估算趋势最好，Li和WostenNote: Kis saturated hydraulic conductivity.

通过灰色关联度分析结果可知，在0～20 cm土层参数与分形维数、干容重、有机质含量关联度最高，参数与分形维数、干容重、黏粒含量关联度最高，参数与砂粒含量、干容重、分形维数关联度最高；在>20～40 cm土层参数与砂粒含量、干容重、有机质含量关联度最高，参数与分形维数、有机质含量、粉粒含量关联度最高，参数与砂粒含量、分形维数、有机质含量关联度最高。采用非线性规划构建van Genuchten模型的参数方程。

在0～20 cm土层模型参数公式如下：

（5）

ln=3.02-4.2×10-3C+0.93BD-3.39+

ln=-0.69+1.65×10-2S+0.06BD+

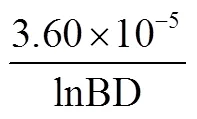
0.642(R=0.77 ,<0.01) （7）

在>20～40 cm土层模型参数公式如下：

=0.08-1.98×10-4S-1.35×10-3BD+

1.11×10-4OM(R=0.75,<0.01) （8）

ln=-0.53-4.10×10-3S-4.70×10-4OM+

1.59+0.24lnS+40.22e-OM

-0.562(R=0.96)<0.01 （9）

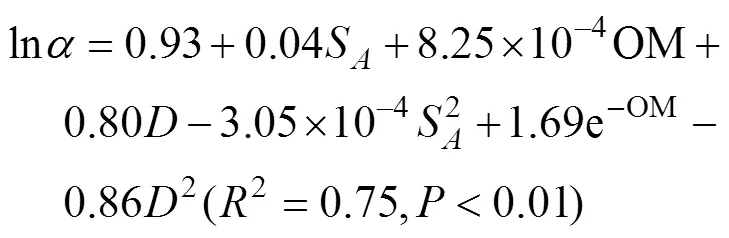
式中C、S、S为黏粒、砂粒、粉粒体积百分数，%；BD为容重，g/cm3；为分形维数；OM为有机质含量，g/kg。

图2为不同土层所构建的土壤传递函数的估算值与实测值之间的关系。由图2可知，土壤传递函数的估算值与实测值基本落在1:1线附近，表明所构建的土壤传递函数估算值与实测值基本吻合，其中参数ln对实测值的估算效果较好。由图2中0～20 cm和>20～40 cm土层模型参数、ln、ln的MAE值可知 MAE值接近于0，表明在不同土层所构建的土壤传递函数的估算值与实测值平均绝对偏离程度较小，估算精度较高。从2值来看，在0～20和>20～40 cm土层模型参数、ln、ln的2值都在0.66以上，可知在0～20 和>20～40 cm土层、ln、ln的土壤传递函数估算值与实测值相近，估算效果较好。从RMSE值来看，在0～20和>20～40 cm土层模型参数、ln、ln的RMSE值接近于0，表明在不同土层所构建的、ln、ln的土壤传递函数估算值与实测值吻合程度较高。

不同土层饱和导水率与土壤理化指标之间的关联度及排序如表2所示。由表2可知，在0～20 和>20～40 cm土层土壤饱和导水率与土壤有机质、干容重、分形维数关联度较高，表明土壤饱和导水率在0～20 cm和>20～40 cm土层与土壤有机质、干容重、分形维数相关程度最高，采用非线性规划法构建饱和导水率的土壤传递函数见式(11)和式(12)。

注：样本数为136. MAE和RMSE单位同纵坐标，下同。

0～20 cm土层：

（2=0.63,<0.01） (11)

>20～40 cm土层：

（2=0.63,<0.01） (12)

图3为根据式（11）和（12）计算的饱和导水率估算值与实测值的关系。由图3可知，除个别点外，饱和导水率的估算值与实测值基本分布在1:1线的两侧。0～20 cm土层，MAE、RMSE、2值分别为0.34 cm/d、0.472 cm/d、0.63；>20～40 cm土层，MAE、RMSE、2值分别为0.47 cm/d、0.691 cm/d、0.61，由此可知，不同土层饱和导水率土壤传递函数估算与实测值相近，表明饱和导水率土壤传递函数估算精度较高。

2.3 土壤水力参数传递函数估算模型验证

根据已构建的土壤传递函数，将剩余27个土样实测数据代入式（5）～式（12），计算得出各参数的估算值，进而得到土壤水分特征曲线和饱和导水率。图4为不同土层根据van Genuchten模型参数土壤传递函数估算土壤含水率和饱和导水率土壤传递函数估算值与实测值关系。由图4可知，在0～20 和>20～40 cm土层土壤含水率散点基本都分布在1:1线两侧；饱和导水率传递函数的估算值在1:1线两侧分散程度较小，表明构建的土壤传递函数估算精度较好。表3为van Genuchten模型参数和饱和导水率土壤传递函数估算值的MAE、RMSE、2值。由表3知，各土层、ln、ln、K的MAE和RMSE值均较小，表明各参数土壤传递函数估算值与实测值相接近。从2值来看，在0～20 cm和>20～40 cm土层、ln、ln、K的2，除0～20 cm土层K的2值为0.68，其他均在0.9以上，表明在不同土层各参数土壤传递函数估算值与实测值基本吻合。总体上本文构建的研究区土壤水力参数传递函数估算精度较高。

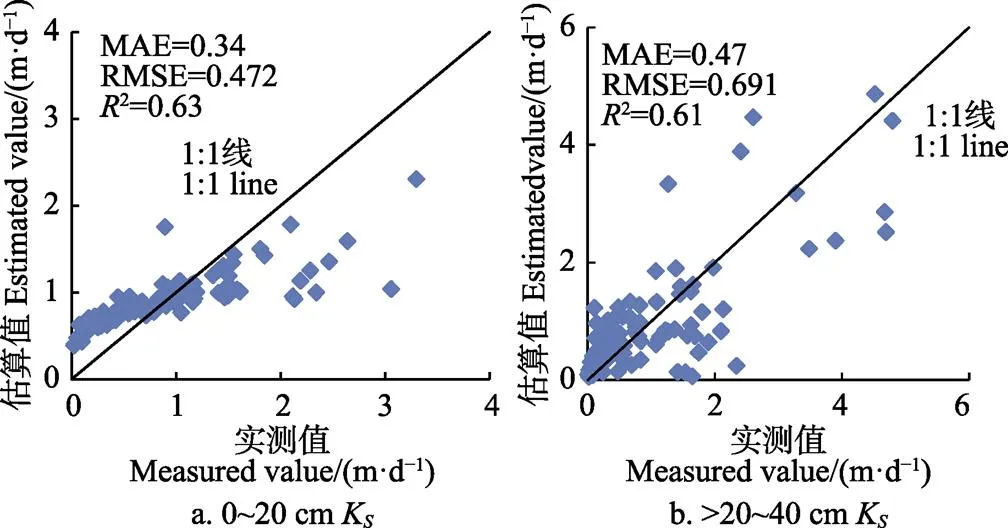
图3 不同土层饱和导水率估算值与实测值的关系

图4 验证阶段不同土层土壤含水率θ和饱和导水率Ks估算值与实测值关系

2.4 本文模型与其他模型对比

采用多元回归等方法构建的土壤水力参数传递函数，分别为Li等[9]、Vereecken等[10]、Wosten等[12]土壤水分特征曲线土壤传递函数和Wosten等[12]、孙丽等[14]、Cosby等[16]饱和导水率土壤传递函数与本文采用非线性规划构建的土壤传递函数（研究区PTFs）进行对比分析。图5为研究区27个点土壤含水率和饱和导水率估算值与实测值关系图。

表3 不同土层van Genuchten模型参数验证

由图5可知，3种土壤传递函数对土壤含水率和饱和导水率估算值与实测值偏差较大，估算效果不理想，研究区PTFs估算值与实测值基本分布在1:1线附近。由图可知，在0～20 cm土层基于Li、Wosten、Vereecken和本文模型4种土壤传递函数估算的体积含水率MAE值分别为0.988、0.373、1.554、0.015 cm3/cm3，可知研究区PTFs估算与实测值平均偏离较小，而其他方法平均偏离程度较大；相应的RMSE值分别为0.076、0.054、0.108、0.022 cm3/cm3，表明Vereecken估算效果最差；从2值来看，研究区PTFs2为0.92，而Li、Vereecken和Wosten的2均小于0.7，表明构建的PTFs估算值与实测值吻合程度较高。在>20～40 cm土层Li、Wosten、Vereecken和本文模型4种土壤传递函数估算的体积含水率MAE值分别为1.879、2.712、1.284、0.021 cm3/cm3，表明Li、Vereecken和Wosten 3种土壤传递函数对实测值估算误差较大；相应的RMSE值分别为0.087、0.133、0.066、0.017 cm3/cm3，研究区PTFs偏差最小，Wosten偏差最大；其他区域3种土壤传递函数2值均小于0.73，而研究区2值为0.94，可知研究区PTFs估算趋势最好，Li和Wosten估算趋势较差。由误差分析可知，本文构建的土壤水分特征曲线的土壤传递函数估算效果均为最优。

由图5可知，Wosten和Sun估算的K相对于1:1线偏离程度较大，估算效果较差。表4为研究区饱和导水率土壤传递函数与Wosten、Sun和Cosby 3种饱和导水率土壤传递函数的误差分析。在0～20 cm土层由4种土壤传递函数估算的K的MAE值可知，4种土壤传递函数估算效果较好；从RMSE值来看，Wosten、Sun、Cosby 3种传递函数估算研究区饱和导水率RMSE都大于0.3 m/d，研究区PTFs估算精度最高，而Wosten估算精度最差；由2值可知，Wosten、Sun和Cosby的2都小于0.45，可知估算值与实测值变化趋势偏不一致，而研究区PTFs估算值与实测值相吻合。在>20～40 cm土层，从4种土壤传递函数MAE值来看，研究区PTFs估算值与实测值最为接近；就RMSE值而言，Wosten、Sun和Cosby估算精度较差，而研究区PTFs估算精度较高；由2值可知，研究区PTFs的2值最大，最能反映实测值变化趋势。通过对比分析可知，本文构建的饱和导水率土壤传递函数估算精度最高、效果最好。

图5 不同土层土壤含水率和饱和导水率估算值与实测值对比

表4 4种方法估算的土壤饱和导水率误差分析

3 讨 论

由于受到土壤容重、土壤质地、土地利用、有机质含量等多种因素的影响，土壤水分特征曲线和饱和导水率具有较强的空间变异性、尺度效应和不确定性，因此，导致了土壤传递函数的区域性特点。

刘继龙等[4]研究表明在杨凌地区影响van Genuchten模型参数的因素随着不同土层而发生变化；朱安宁等[29]研究表明在封丘地区van Genuchten模型参数与土壤质地、有机质含量、容重等存在相关性；Vereecken等[10]对比利时地区研究结果表明van Genuchten模型参数与砂粒、黏粒、容重、有机碳这几种影响因素关系密切，这与本文van Genuchten模型参数的主要影响因素存在一定差异，这可能是由于研究区不同而造成的。分形维数是衡量土壤质地粗细程度的一个指标，本文引入土壤分形维数这一影响因素，研究表明在0～20 和>20～40 cm土层土壤残余含水率与干容重、有机质含量、砂粒含量密切相关，主要是由于随着土壤容重的变化孔隙度也发生变化，土壤持水能力也随之发生变化；而土壤有机质含量增加会使土壤结构发生变化，小孔隙增多，比表面积增大，对水的吸附力加大，从而使土壤的持水能力增强；砂粒含量增多会使土壤大孔隙增多，从而使土壤持水能力变弱[30]。参数是与土壤进气值有关的参数，在0～20 cm土层参数与砂粒含量、干容重、分形维数密切相关，而在>20～40 cm土层参数与砂粒含量、有机质、分形维数关系密切。参数是与土壤孔径分布有关的参数，其值与分形维数呈负相关[31]，本文研究表明不同土层参数与分形维数关系最为密切。同时把分形维数作为其中1个自变量与其他重要影响因素共同构建土壤传递函数，获得了较高的预测精度。另外，把分形维数作为唯一自变量构建van Genuchten模型参数的土壤传递函数的可行性有待进一步研究。

由饱和导水率与土壤理化特性灰色关联度分析可知，影响饱和导水率的主要因素为分形维数、容重、有机质。这与赵云鹏等[32-34]研究结果不一致，说明不同地区饱和导水率影响因素也存在差异。本文情况可能是研究区黑土有机质含量高，可以促进团聚体形成，从而改善土壤结构，导致饱和导水率发生改变[35]。

本文采用非线性规划建立研究区土壤水分特征曲线和饱和导水率土壤传递函数，有效解决了极值点处出现较大偏差的问题，使预测值估算逼近实测值，提高了预测精度。但是，非线性规划与线性回归、非线性回归等方法相似，都存在不能准确描述土壤水力参数与土壤理化性质之间的物理机制，建立的模型不具有物理意义。

由于土壤水分特征曲线采用高速离心机测定，测定过程中会导致土壤容重发生变化，从而产生一定的误差。另外，一些采样点的预测精度偏低，可能是由于采样过程中采集了较为松散或者板结的土壤，导致土壤水力测参数的测定出现偏差。

4 结 论

1）本文以松嫩平原黑土区南部为研究区域，采用灰色关联分析法对土壤理化性质指标与van Genuchten模型参数和饱和导水率进行分析，土壤分形维数、有机质含量、干容重及土壤颗粒组成都在不同土层各参数中起到至关重要作用，其中分形维数同各参数的关联度较大。

2）本文把分形维数作为自变量，并采用非线性规划建立研究区不同土层van Genuchten模型参数和饱和导水率的土壤传递函数，通过对各参数土壤传递函数进行验证，在0～20 cm和>20～40 cm土层残余含水率土壤进气值倒数ln土壤孔径分布指数ln饱和导水率K的平均相对误差（mean relative error，MAE）值接近于0；而lnln、K的均方根误差（root mean square error，RMSE）值均较小；决定系数2值基本都在0.66以上。表明所构建的传递函数估算精度高，可用于研究区土壤水力参数的研究。

3）对比Li、Vereecken、Wosten土壤水分特征曲线土壤传递函数以及Wosten、Sun、Cosby饱和导水率土壤传递函数估算研究区土壤水力参数，在0～20和>20～40cm土层Li、Vereecken、Wosten土壤水分特征曲线土壤传递函数对研究区土壤含水率估算MAE和RMSE值均大于研究区传递函数误差值，且2值都小于0.73。在0～20和>20～40 cm土层Wosten、Sun、Cosby饱和导水率土壤传递函数估算研究区饱和导水率RMSE都大于0.3 m/d，估算较差，而2都小于0.45，都大于研究区构建传递函数误差，因此，表明本文构建的土壤水力参数传递函数估算效果明显优于其他方法，且区域适应性较强。

[1] Merdun H，Cinar O，Meral R，et al. Comparison of artificial neural network and regression pedotransfer functions for prediction of soil water retention and saturated hydraulic conductivity[J].Soil and Tillage Research, 2006, 90(1): 108－116.

[2] 廖凯华，徐绍辉，吴吉春，等. 不同土壤转换函数预测砂土非饱和导水率的对比分析[J]. 水科学进展，2013，24(4)：560－567. Liao Kaihua, Xu Shaohui, Wu Jichun, et al.Estimating unsaturated hydraulic conductivity of sandy soils using different pedotransfer functions[J]. Advances in Water Science, 2013, 24(4): 560－567. (in Chinese with English abstract)

[3] Zeleke T B, Si B C. Characterizing scale-dependent spatial relationships between soil properties using multifractal techniques[J]. Geoderma, 2006, 134(3): 440－452.

[4] 刘继龙，马孝义，张振华，等. 基于联合多重分形的土壤水分特征曲线土壤传递函数[J]. 农业机械学报，2012，34(3)：51－55. Liu Jilong, Ma Xiaoyi, Zhang Zhenhua, et al.Pedotransfer functions of soil water retention curve based on joint multifractal[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 34(3): 51－55. (in Chinese with English abstract)

[5] 黄元仿，李韵珠. 土壤水力性质的估算—土壤转换函数[J]. 土壤学报，2002，39(4)：517－523. Huang Yuanfang, Li Yunzhu. Estimation of soil hydraulic properties—pedo-transfer functions[J]. Acta Pedologica Sinica, 2002, 39(4): 517－523. (in Chinese with English abstract)

[6] Liu Z X, Shu Q S, Wang Z Y. Apply pedo-transfer functions to simulate spatial heterogeneity of cinnamon soil water retention characteristics in western liaoning province[J]. Water Resources Management, 2007, 21(10): 1751－1762.

[7] Schaap M G, Leij F J, van Genuchten M T. Neural network analysis for hierarchical prediction of soil hydraulic properties[J]. Soil Science Society of America Journal, 1998, 62(4): 847－855.

[8] Minasny B, Mcbratney A. The neuro-m method for fitting neural network parametric pedotransfer functions[J]. Soil Science Society of America Journal, 2002, 66(2): 352－361.

[9] Li Y，Chen D, White R E, et al. Estimating soil hydraulic properties of Fengqiu County soils in the North China Plain using pedo-transfer functions[J]. Geoderma, 2007, 138(3): 261－271.

[10] Vereecken H, Maes J, Feyen J, et al. Estimating the soil moisture retention characte ristic from texture, bulk density, and carbon content[J]. Soil Science, 1989, 148(6): 389－403.

[11] Schaap M G, Leij F J, Genuchten M Th. ROSET TA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions[J]. Journal of Hydrology, 2001, 251(3): 163－176.

[12] Wosten J H M, Lilly A, Nemes A, et al. Development and use of a database of hydraulic properties of Europ pean soil[J]. Geoderma, 1999, 90(3): 169－185.

[13] 孙美，张晓琳，冯绍元，等. 基于交叉验证的农田土壤饱和导水率传递函数研究[J]. 农业机械学报，2014，45(10)：147－152. Sun Mei, Zhang Xiaolin, Feng Shaoyuan, et al. Pedo-transfer function for saturated hydraulic conductivity of agricultural soil based on cross-validation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(10): 147－152. (in Chinese with English abstract)

[14] 孙丽，刘廷玺，段利民，等. 科尔沁沙丘-草甸相间地区表土饱和导水率的土壤传递函数[J]. 土壤学报，2015，52(1)：68－76. Sun Li, Liu Tingxi, Duan Limin, et al. Prediction of saturated hydralic conductivity of surface soil in sand-dune-and- meadow inte rlaced region of Horqin with pedo-transfer functions method.[J]. Acta Pedologica Sinica, 2015, 52(1): 68－76. (in Chinese with English abstract)

[15] Campbell G S. Soil physics with basic: Transport models for soil-plant system[J]. Journal of Hydrology, 1987, 90(3): 359－360.

[16] Cosby B J, Hornberger G M, Clapp R B, et al. A statistical exploration of the relationships of soil moisture characteristics to the physical properties of soils[J].Water Resources Research, 1984, 20(6): 682－690.

[17] Saxton K E, Rawls W J, Romberger J S, et al. Estimating generalized soil-water characteri- stics from texture[J].Soil Science Society of America Journal,1986, 50(4): 1031－1036.

[18] 王子龙，陈伟杰，付强，等. 基于优先级指数的土壤采样设计方法研究[J]. 农业机械学报，2018，49(7)：244－251. Wang Zilong, Chen Weijie, Fu Qiang, et al. Method of soil sampling design based on priority index[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(7): 244－251. (in Chinese with English abstract)

[19] 王国梁，周生路，赵其国. 土壤颗粒的体积分形维数及其在土地利用中的应用[J]. 土壤学报，2005，42(4)：545－550. Wang Guoliang, Zhou Shenglu, Zhao Qiguo. Volume fractal dimension of particles and it’s applications to land use[J]. Acta Pedologica Sinica, 2005, 42(4): 545－550. (in Chinese with English abstract)

[20] 中华人民共和国农业部. 土壤检测第6部分：土壤有机质测定：NY/T 1121.6-2006[S]. 北京：中国农业出版社，2006.

[21] Wim M Cornelis, Jan Ronsyn, Marc Van Meirvenne. Evaluation of pedotransfer functions for predicting the soil moisture retention curve[J]. Soil Science, 2001(65): 638－648.

[22] 陈俊英，柴红阳，Leionid G，等. 再生水水质对斥水和亲水土壤水分特征曲线的影响[J]. 农业工程学报，2018，34(11)：121－127. Chen Junying, Cai Hongyang, Leionid G, et al.Impact of treated waste water quality on repellent and wettable soil water characteristic curve[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(11): 121－127. (in Chinese with English abstract)

[23] 姚姣转，刘廷玺，王天帅，等. 科尔沁沙地土壤水分特征曲线传递函数的构建与评估[J]. 农业工程学报，2014，30(20)：98－108. Yao Jiaozhuan, Liu Tingxi, Wang Tianshuai, et al.Development and evaluation of pedo-transfer functions of soil water characteristic curves in Horqin sandy land[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(20): 98－108. (in Chinese with English abstract)

[24] van Genuchten M T.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]Soil Science Society of America Journal, 1980, 44(44): 892－898.

[25] 郭向红，孙西欢，马娟娟. 基于混合遗传算法估计 van Genuchten 方程参数[J]. 水科学进展，2009，20(5)： 677－682. Guo Xianghong, Sun Xihuan, Ma Juanjuan. Parametric estimation of the van Genuchten's equation based on hybrid genetic algorithm[J]. Advances in Water Science, 2009, 20(5): 677－682. (in Chinese with English abstract)

[26] 付强，蒋睿奇，王子龙，等. 基于改进萤火虫算法的土壤水分特征曲线参数优化[J]. 农业工程学报，2015，31(11)：117－122. Fu Qiang, Jiang Ruiqi, Wang Zilong, et al. Optimization of soil water characteristic curves parameters by modified firefly algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(11): 117－122. (in Chinese with English abstract)

[27] 付强，颜培儒，李天霄，等. 冻融期不同覆盖和气象因子对土壤导热率和热通量的影响[J]. 农业工程学报，2017，33(20)：98－105. Fu Qiang, Yan Peiru, Li Tianxiao, et al. Influence of different coverage and meteorological factors on soil thermal conductivity and heat flux during freezing and thawing period[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(20): 98－105. (in Chinese with English abstract)

[28] Deng J L.Introduction to Grey-system theory[J]. The Journal of Grey System, 1989, 1(1): 1－24.

[29] 朱安宁，张佳宝，陈效民，等. 封丘地区土壤传递函数的研究[J]. 土壤学报，2003，40(1): 53－58. Zhu Anning, Zhang Jiabao, Chen Xiaomin, et al. Study on pedo-transfer function in Fengqiu[J]. Acta Pedologica Sinica, 2003, 40(1): 53－58. (in Chinese with English abstract)

[30] 郑子成，李卫，李廷轩，等. 基于分形理论的土壤水分特征曲线研究[J]. 农业机械学报，2012，43(5)：49－54. Zheng Zicheng, Li Wei, Li Tingxuan, et al. Soil water retention curve based on fractal theory in greenhouse soil[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(5): 49－54. (in Chinese with English abstract)

[31] 徐绍辉，刘建立. 估计不同质地土壤水分特征曲线的分形方法[J]. 水利学报，2003，34(1)：78－82. Xu Shaohui, Liu Jianli. Fractal approach for estimating soil water retention curves of various textures[J]. Journal of Hydraulic Engineering, 2003,34(1): 78－82. (in Chinese with English abstract)

[32] 赵云鹏，白一茹，王幼奇，等. 宁夏引黄灌区土壤饱和导水率空间分异特征[J]. 北方园艺，2017(8)：166－171. Zhao Yunpeng, Bai Yiru, Wang Youqi, et al. Spatial variability of soil saturated hydraulic conductivity in the yellow river irrigated area in ningxia[J]. Northern Horticulture, 2017(8): 166－171. (in Chinese with English abstract)

[33] 李孝良，陈效民，周炼川，等. 西南喀斯特地区土壤饱和导水率及其影响因素研究[J]. 灌溉排水学报，2008，27(5)：74－76. Li Xiaoliang, Chen Xiaomin, Zhou Lianchuan, et al.Soil saturated hydraulic conductivity and its influential factors in southwest karst region of china[J]. Journal of Irrigation and Drainage, 2008, 27(5): 74－76. (in Chinese with English abstract)

[34] 赵春雷，邵明安，贾小旭. 黄土高原北部坡面尺度土壤饱和导水率分布与模拟[J]. 水科学进展，2014，25(6)： 806－815. Zhao Chunlei, Shao Ming'an, Jia Xiaoxu.Distribution and simulation of saturated soil hydraulic conductivity at a slope of northern loess plateau[J]. Advances in Water Science, 2014, 25(6): 806－815. (in Chinese with English abstract)

[35] 张耀方，赵世伟，王子龙，等. 黄土高原土壤团聚体胶结物质的分布及作用综述[J]. 中国水土保持科学，2015，13(5)：145－150. Zhang Yaofang, Zhao Shiwei, Wang Zilong, et al.Distribution and function of cementing materials of soil aggregates on the Loess plateau，western China[J]. Science of Soil and Water Conservation, 2015, 13(5): 145－150. (in Chinese with English abstract)

Constructing pedo-transfer functions based on grey relational and nonlinear programming to estimate hydraulic parameters in black soil

Wang Zilong, Chang Guangyi, Jiang Qiuxiang※, Fu Qiang, Chen Weijie, Lin Baijian, Yin Yuming

(150030,)

Soil water characteristic curve and saturated hydraulic conductivity are important parameters for constructing soil moisture and solute transport models, both of which are affected by soil texture, bulk density, organic matter content, porosity, etc. In order to simply and accurately obtain the 2 parameters above, a total of 136 soil sampling points in the southern part of the black soil area in the Songnen Plain were designed, and the soil samples in 2 layers of these sampling points were collected to measure the soil water characteristic curve, saturated hydraulic conductivity and soil physical and chemical properties, the grey correlation analysis was used to determine the main soil physical and chemical properties affecting soil hydraulic parameters.The results showed: 1) in 0-20 cm soil layer, the residual moisture contentof van Genuchten model had the higher correlation with fractal dimension, dry bulk density and organic matter content, and the correlation between parameter pore distribution index and fractal dimension, dry bulk density and clay content was the highest. The parameter of reciprocal soil air influx had the higher correlation with sand content, dry bulk density and fractal dimension. In soil layer from 20 to 40 cm, the parameter of residual moisture contentof van Genuchten model had the higher correlation with sand content, dry bulk density and organic matter content; the parameter pore distribution index and fractal dimensions had the highest correlation; The correlation between fractal dimension, organic matter content and silt content and parameter pore distribution index was the highest, and the correlation between parameter reciprocal soil air influx and sand content, fractal dimension and organic matter content was the highest. 2) The correlation between soil saturated hydraulic conductivity and soil organic matter, dry bulk density and fractal dimension in 0-40 cm soil layer was higher. 3) The pedo-transfer functions of the soil water characteristic curve and the saturated hydraulic conductivity based on soil fractal dimension, organic matter, dry bulk density and soil particle composition were established by using the nonlinear optimal programming method. The accuracy of the pedo-transfer functions established in the study was verified by comparing with the existing common pedo-transfer functions. The results showed that soil fractal dimension was one of the primary parameters in constructing soil pedo-transfer functions to predict soil water characteristic curve and saturated hydraulic conductivity. In addition, soil dry bulk density and organic matter content also played an important role in pedo-transfer functions of different soil layers. Based on the verification analysis, the mean absolute errors of the estimated soil hydraulic parameters in different soil layers were all close to 0, and the root mean square error values of the predicted soil hydraulic parameters in different soil layers were also small. Specially, the root mean square errors of soil moisture content estimated by pedo-transfer functions established in the study were 0.022 and 0.017 cm3/cm3in different soil layers, respectively. On the basis of comparing with the other existing common pedo-transfer functions of soil water characteristic curve and saturated hydraulic conductivity, the pedo-transfer functions of soil hydraulic parameters established in the study had high estimation accuracy, the root mean square error values were small; the determination coefficient values were all above 0.66, which was better than the other existing common pedo-transfer functions. In summary, the pedo-transfer functions of the soil water characteristic curve and saturated water conductivity established in the study can be used to estimate the soil hydraulic parameters in the black soil area of the Songnen Plain, and also provide technical support for acquisition of regional soil hydraulic properties.

soils; gray correlation; water content; black soil area of Songnen Plain; soil water characteristic curve; saturated hydraulic conductivity; pedo-transfer functions

10.11975/j.issn.1002-6819.2019.10.008

S152.7

A

1002-6819(2019)-10-0060-09

2018-10-23

2019-03-10

国家自然科学基金（51579045）；东北农业大学“学术骨干”基金资助项目（16XG10）

王子龙，教授，博士，主要从事寒区农业水土资源高效利用研究。Email：wangzilong@neau.edu.cn

姜秋香，副教授，博士，主要从事水土资源高效利用和管理研究。Email：jiangqiuxiang2017@163.com

王子龙，常广义，姜秋香，付 强，陈伟杰，林百健，印玉明. 灰色关联及非线性规划法构建传递函数估算黑土水力参数[J]. 农业工程学报，2019，35(10)：60－68. doi：10.11975/j.issn.1002-6819.2019.10.008 http://www.tcsae.org

Wang Zilong, Chang Guangyi, Jiang Qiuxiang, Fu Qiang, Chen Weijie, Lin Baijian, Yin Yuming. Constructing pedo-transfer functions based on grey relational and nonlinear programming to estimate hydraulic parameters in black soil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(10): 60－68. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.10.008 http://www.tcsae.org