回归方程法测定两个龙眼品种叶面积研究

潘介春，黄 幸，邓英毅，丁 峰，徐炯志，徐石兰，黄思婕，杨亚涵，龙蔷宇，王金英，李 琳，王 颖

(广西大学农学院，广西 南宁 530004)

叶片是植物进行光合作用、蒸腾作用、呼吸作用、合成有机物的重要器官，叶面积是反映植物生长发育、遗传特性等生理生化过程的主要参数之一[1]，它对植物的光能利用、水分蒸发量、干物质积累、收获量及经济效益有显著影响[2]。龙眼的叶片面积直接关系到光合产物量，影响果实的产量与品质，也是设计栽培模式、制定整形修剪方案、指导合理密植、调整群体结构、变量施肥和精确喷灌以获得高产等的重要依据之一。回归方程法具有简单、非破坏性、可活体测量的特点，被广泛应用于植物叶面积估算[3—14]。

龙眼Dimocarpus longan是重要的亚热带果树之一，主产于中国西南部至东南部地区，以广东最盛，福建次之[15]。目前，有关利用回归方程法测定龙眼叶面积的研究国内仍未见报道。‘储良’龙眼是广东省茂名市在二十世纪九十年代选育的龙眼新品种，是自然突变和自然淘汰形成的优良单株[16]；‘石硖’龙眼原产于广东南海，是鲜食干制优良品种[3]。两个品种皆为广东、广西主栽品种[17]。本研究利用回归方程法测算‘储良’和‘石硖’两个品种叶面积。该方法首先将龙眼的一小部分叶片采摘下来，利用叶面积仪测定叶片的长度、宽度、周长、叶面积等叶形指标，通过叶形指标建立叶面积的回归方程。在后续实际应用中，可在不破坏植物叶片的情况下，用尺子测量两个龙眼品种成熟叶片的叶长、叶宽，代入相应的回归方程，即可估测其叶面积，为生产实践提供生长量统计的可靠依据。

1 材料与方法

1.1 材料

以广西大学农学院教学科研基地龙眼园栽培的‘储良’、‘石硖’两个龙眼品种为试材，参照两种桑科植物[3]、7 个早熟梨品种[7]、荔枝Litchi chinensis[18]等叶面积的研究方法，在树冠东、西、南、北随机选择大小不一、发育正常、生长健壮、无缺损的成熟展开的叶片作为测量样本，每品种各取50 片，放入保鲜袋内，防止叶片失水变形。带回实验室，经清洗、晾干后测定。

1.2 方法

每品种随机选取30 片叶用于回归分析，分别编号后，用便携式叶面积仪(CI-203)测定所有叶片的叶长、叶宽、叶周长和叶面积指标。用Excel 软件整理数据，SPSS 18.0 软件对各项数据进行独立样本T检验、相关性分析、回归分析。

2 结果与分析

2.1 两个龙眼品种叶形指标比较

由表1 可知，‘储良’只有叶周长、叶长/叶宽指标大于‘石硖’，其余叶宽、叶长、叶宽×叶宽、叶长×叶长、叶长×叶宽、叶面积指标均小于‘石硖’。分别对两个龙眼品种的叶周长、叶长、叶宽、叶长/叶宽、叶宽×叶宽、叶长×叶长、叶长×叶宽、叶面积进行独立样本T 检验，P 值均大于0.05，表明两个龙眼品种的叶形指标差异均不显著。

表1 两个龙眼品种的叶形指标比较Table 1 Comparison on leaf shape indicators of two longan cultivars

2.2 两个龙眼品种叶面积与叶形指标的相关性

由表2 知，‘储良’、‘石硖’的叶面积与叶周长、叶长、叶宽、叶长/叶宽、叶宽×叶宽、叶长×叶长、叶长×叶宽7 个指标之间存在极显著正相关。两个品种的叶面积与叶长×叶宽之间的相关系数最大。表明两个龙眼品种的叶面积以叶周长、叶长、叶宽、叶长/叶宽、叶宽×叶宽、叶长×叶长、叶长×叶宽等7个指标均可建立较好的回归方程。

表2 两个龙眼品种叶面积与叶形指标的Pearson 相关性分析Table 2 Pearson correlation analysis of leaf area and leaf shape index of two longan cultivars

2.3 两个龙眼品种叶面积回归方程建立

以相关性较高且极显著的7 个叶形指标对两品种龙眼的叶面积进行一元线性、对数函数、逆函数、二次方、三次方、复合函数、幂函数、指数函数、S 形曲线等9 种回归方程分析，各回归方程拟合优度R2见表3。‘储良’以周长、叶宽、叶长、叶长/叶宽、叶宽×叶宽、叶长×叶长、叶长×叶宽为指标拟合的回归方程R²分别为0.676～0.942、0.779～0.876、0.558～0.954、0.389～0.698、0.767～0.877、0.351～0.953、0.688～0.979。‘石硖’以周长、叶宽、叶长、叶长/叶宽、叶宽×叶宽、叶长×叶长、叶长×叶宽为指标拟合的回归方程R²分别为0.845～0.936、0.703～0.751、0.803～0.923、0.406～0.443、0.678～0.781、0.707～0.922、0.833～0.999。结果表明，以各种叶形指标建立的叶面积9 个回归方程，两个龙眼品种叶面积与7 个叶形指标之间拟合效果都较好，说明叶周长、叶长、叶宽、叶长/叶宽、叶宽×叶宽、叶长×叶长、叶长×叶宽这7 个叶形指标均可用于2 个龙眼品种叶面积的估算。但以叶长×叶宽建立的叶面积回归方程的拟合效果最好，R2最高，且相关系数最高，说明两个龙眼品种用叶长×叶宽为指标建立的叶面积方程更准确可靠。因此以叶长×叶宽为自变量建立9 种叶面积回归方程，结果见表4。

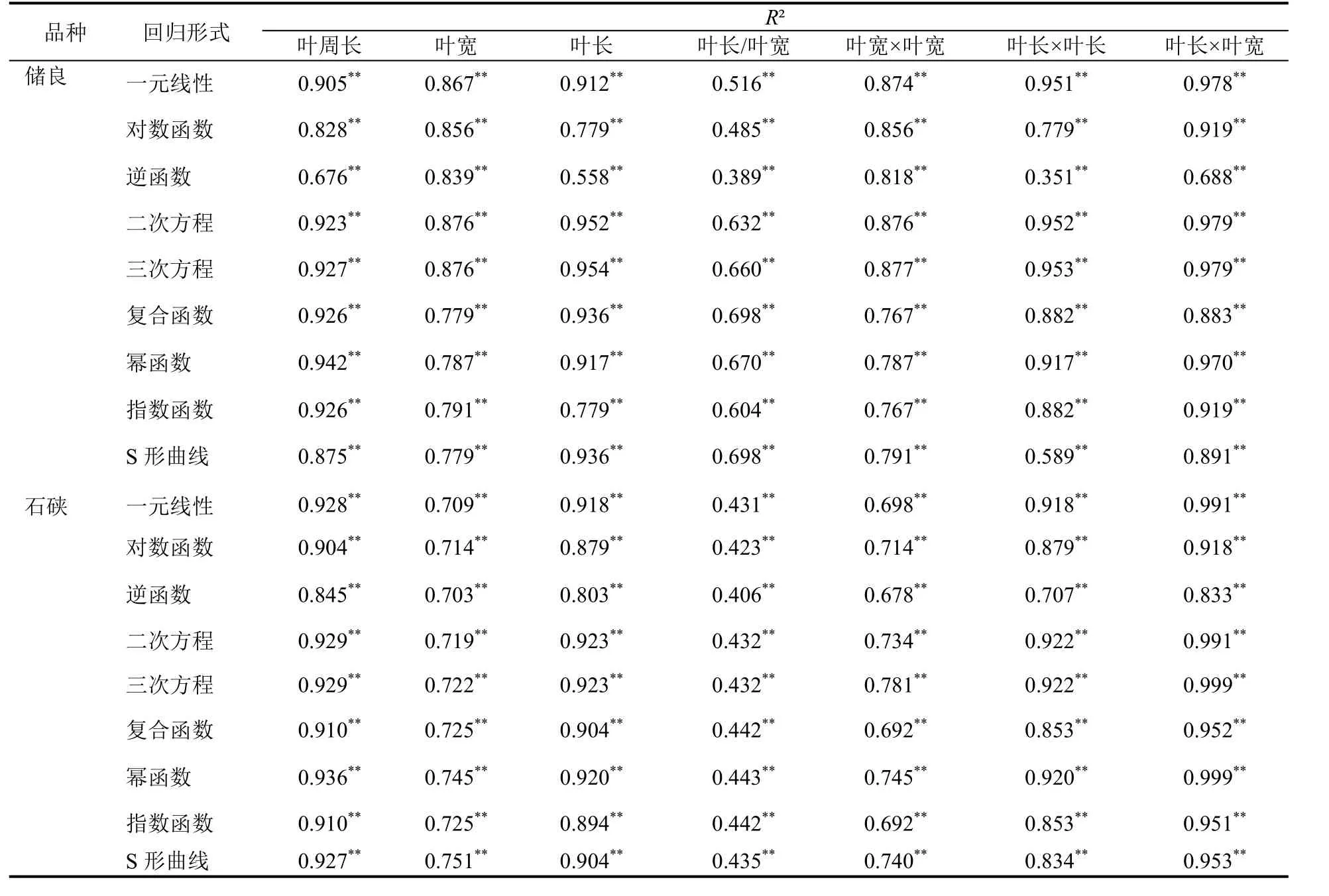
表3 两个龙眼品种7 个叶形指标的9 个回归方程拟合优度Table 3 Fitting goodness of 9 regression equations for 7 leaf shape indexes of two longan varieties

表4 两个龙眼品种基于叶长×叶宽的叶面积回归方程Table 4 Regression equation of leaf length×wide leaf area based on two longan varieties

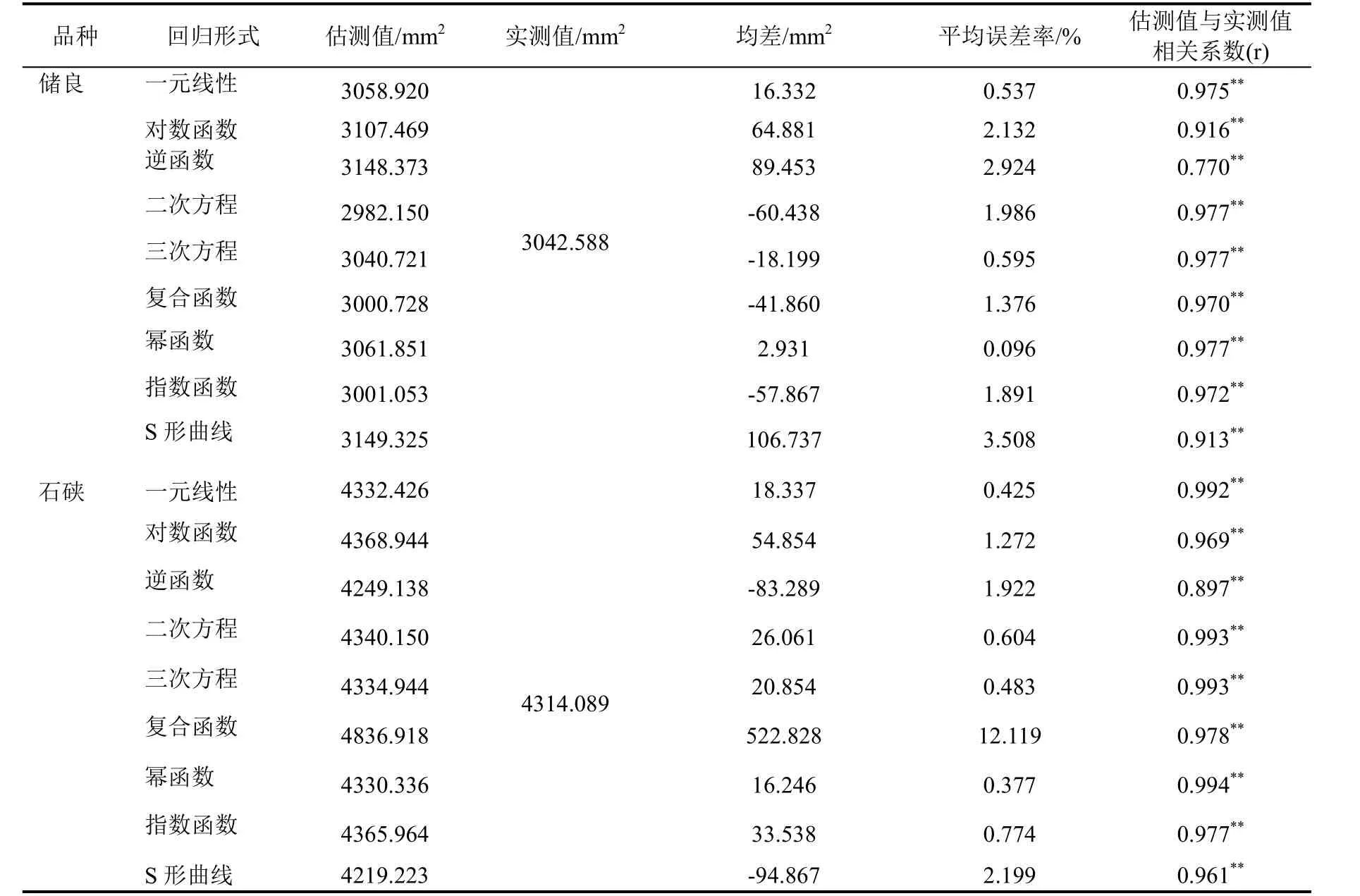
表5 两品种龙眼叶面积实测值与基于叶长×叶宽回归方程估测值比较Table 5 Comparisons between the measured values of leaf area of two longan varieties and the estimated values based on the regression equation of leaf length and leaf width

2.5 适合两个龙眼品种总叶面积的回归方程建立与检验

以‘储良’、‘石硖’作叶面积回归分析的60 张叶片进行总的叶面积回归分析，对基于叶长×叶宽的两品种龙眼总叶面积进行回归分析，能建立较好估测龙眼叶面积的一元线性、二次方程、三次方程、幂函数。结果表明，一元线性、二次方程、三次方程、幂函数的R2都较高，能较好地估测龙眼叶面积(表6)，其中幂函数R2最高。分别用两品种龙眼剩下的各20 片叶的实测值与总的叶面积方程估测值进行可靠性检验(表7)，发现两个龙眼品种基于叶长×叶宽所得的四个回归方程叶面积估测值与实测值之间均呈极显著相关，基于叶长×叶宽的幂函数方程所得的叶面积估测值与实测值均差和误差率最小，精度最高，且估测值与实测值相关系数最大(r=0.992)，较适合用于龙眼叶面积估测。因此幂函数方程y=0.869x0.988能用来模拟或预测基于叶长×叶宽的两品种龙眼叶面积。

表6 两个龙眼品种基于叶长×叶宽的叶面积总回归方程Table 6 Total regression equation of leaf area for two longan varieties based on leaf length×leaf width

表7 两品种龙眼总叶面积的实测值与基于叶片长×叶宽回归方程的估测值比较Table 7 Comparisons between the measured total leaf area of two longan varieties and the estimated value based on the regression equation of leaf length×leaf width

3 讨论

叶面积仪(CI-203)为便携式激光叶面积仪，可直接测量叶片长度、宽度、周长、叶面积等叶形指标，为实测值，但测量时操作要求较为严格，且测量位点需保持一致。若操作不规范，或者每次测量位点不一致，所测叶片长度、宽度、周长、叶面积等叶形指标有较大误差。单独使用叶面积仪测定叶面积时采摘的大量叶片会直接破坏树体，不利于样本植株生长，且需大量测量叶面积指标时操作较麻烦。利用回归方程法测算叶面积，只需采摘树体小部分叶片，通过样本的叶形指标计算出最优的叶面积模拟回归方程。在后续实际应用中，无需破坏树体，直接通过直尺或软尺等较易操作的测量工具测量叶长和叶宽指标，代入已测算出来的误差最小的叶面积回归方程，得到叶面积的估算值。因此，回归方程法测算叶面积与叶面积仪测量叶面积比较，前者操作方法更简便省时，为后续长期大量测量叶面积数据提供了更为简便省时的测算方式。

本研究表明，‘储良’和‘石硖’两品种龙眼的叶面积与其叶周长、叶长、叶宽、叶长/叶宽、叶宽×叶宽、叶长×叶长、叶长×叶宽之间均呈极显著相关，且叶面积与基于叶长×叶宽的回归方程估算值相关系数最大。基于上述7 个叶形指标建立的一元线性、对数函数、逆函数、二次方程、三次方程、复合函数、幂函数、指数函数、S 形曲线等9 种叶面积回归方程的拟合优度R2均达极显著水平，表明7 个叶形指标的9 个回归方程均可用于估算‘储良’和‘石硖’的叶面积。基于叶长×叶宽建立的9 种叶面积回归方程R2均最高，拟合效果最好，与前人的研究等相似[8—9,11—14]。因此，叶长×叶宽可作为叶面积估测的首选指标。

基于叶长×叶宽建立的9 个叶面积回归方程的验证分析表明，‘储良’和‘石硖’以幂函数方程所得的R2较高，且叶面积估测值与实测值误差最小，精度最高。因此，基于叶长×叶宽的两个品种龙眼叶面积指标的幂函数方程可作为其叶面积估测优先选择的模型。‘储良’和‘石硖’对应的较为精准的叶面积回归方程分别为y= 0.751x1.006和 y= 0.986x0.973。

对基于叶长×叶宽适合两个龙眼品种总叶面积估测的模型进行分析，结果表明，一元线性、二次方程、三次方程、幂函数都有较高的拟合优度R2，且均差和误差率较小，精确度高，能较好估测叶面积。故基于叶长×叶宽的一元线性、二次方程、三次方程、幂函数都可用于估测两个龙眼品种的叶面积，其中幂函数均差和误差率最小，估测精确度最高，较适于估测龙眼叶面积。因此，适合这两个品种龙眼的叶面积幂函数方程为y=0.869x0.988。

本研究提出的回归方程适用于‘储良’和‘石硖’两个龙眼品种，是否适合龙眼其他品种还需进一步验证。建立叶面积回归方程后，在实际应用中，可在不破坏植物叶片的前提下，测定两龙眼品种成熟叶片的长、宽，代入相应的回归方程中估测其叶面积。