高速工况下乘员耳侧噪声信号重构方法

杨东坡，王孝兰，王岩松，郭辉，刘宁宁



高速工况下乘员耳侧噪声信号重构方法

杨东坡，王孝兰，王岩松，郭辉，刘宁宁

(上海工程技术大学汽车工程学院，上海 201620)

高速工况下，车内噪声信号具有随机性和波动性的特征。将一种基于经验模态分解(Empirical Mode Decomposition, EMD)和反向传输(Back Propagation, BP)神经网络的算法，用于重构车内乘员耳侧噪声信号。首先通过对车内乘员耳侧噪声贡献量分析，确定关键噪声源信号；其次对选择的噪声源信号进行EMD分解，得到有限个相对平稳的固有模态函数(Intrinsic Mode Function, IMF)分量；然后采用极值点划分法，按各个分量的波动情况进行重新划分，将信号分量重构为高频、中频和低频3个分量；最后对不同频段的部分建立相应BP神经网络模型，并将不同频段分量的重构结果叠加作为原信号的重构结果。以在某轿车采集到的5个噪声信号源为基础，利用该方法进行乘员耳侧噪声信号重构，并对其进行分析。结果表明：提出的噪声重构方法可以实现高速工况乘员耳侧噪声信号的重构，并具有良好的性能。

高速工况；车内噪声；经验模态分解；BP神经网络；信号重构

0 引 言

为了实现高速工况下车内乘员耳侧噪声的主动控制(Active Noise Control, ANC)，首先要为控制系统提供初级参考信号。噪声主动控制系统要求参考信号能够尽可能地提供初级声源的相关信息。对于初级参考信号的拾取，传统方法是在乘员耳侧附近安装传声器以获取初级参考信号，此方法不可避免地引入了次级声源二次污染，不利于系统的快速收敛，因此研究车内乘员耳侧噪声的重构方法，获取ANC的参考信号具有一定的意义。

目前，解决声场重构问题的主要方法包括近场声全息(Near-field Acoustics Holography, NAH)和多传感器数据融合(Multi-sensor Data Fusion, MSDF)等。NAH方法已经从稳态平面声源声场重构发展到瞬态任意形状声源声场重构，主要包括：移动框架(Moving Frame Acoustic Holography, MFAH)[2]，统计最优近场声全息(Statistically Optimal NAH, SONAH)[3]，等效源法近场声全息(Equivalent Source Method, ESM-based NAH)[4]等方法。此类方法主要用于声源识别与故障诊断，对低频信号的声场重构效果不佳。MSDF方法可通过多类同构或异构传感器的数据融合，获取对被观测目标的一致性的认识。MSDF方法已经从卡尔曼滤波法、贝叶斯估计法等传统方法发展到智能方法。其中，常振臣[5-6]提出了基于神经网络的方法对车内噪声信号的预测，解决了次级声源对初级声场声反馈的问题，但其未分析高速工况的问题，且非稳态工况存在明显误差。苏丽俐[7]采用粒子群优化最小二乘支持向量机(Particle Swarm Optimization-Least Squares- Support Vector Machine, PSO-LS-SVM)算法，实现了对匀速工况下驾驶员耳侧噪声信号的仿真辨识，初步验证了采用多传感器数据融合(MSDF)方法进行车内噪声信号重构的可行性。汽车高速行驶(大于等于80 km·h-1)时，影响车内乘员耳侧噪声的源信号众多，车内噪声又具有时变性，而且噪声的构成和产生机理非常复杂，利用多源信号，基于智能融合算法，可以实现乘员耳侧噪声信号重构。常用的智能算法包括反向传输(Back Propagation, BP)神经网络、模糊逻辑识别(Fuzzy Logic Identification, FLI)、支持向量机(Support Vector Machine, SVM)等，其中，BP神经网络具有很好的非线性拟合能力，单独使用神经网络可以很好地处理信号的非线性，但非平稳性带来的误差不可避免[8]。

因此，本文基于经验模态分解(EMD)和BP神经网络算法，重构车内乘员耳侧噪声时域信号。首先通过贡献量分析选择贡献量大的点作为测量点，然后经EMD分解将神经网络输入信号变成一组相对平稳的序列，再结合神经网络进行乘员耳侧噪声时域信号重构，并通过实车道路试验验证了算法的有效性。

1 基本理论与算法

1.1 EMD分解基本原理

经验模态分解(EMD)是一种具有自适应性的信号处理方法，由HUANG N E等[1]于1998年提出。

从本质上来讲，EMD方法是基于信号自身时间尺度，将采集的信号进行平稳化处理，其结果是信号根据不同的波动程度被逐渐分解，得到有限个具有不同特征尺度的数据序列，即固有模态函数(Intrinsic Mode Function, IMF)分量。此方法与傅里叶变换和小波分解等方法有着本质的差别，它不需要预先给定任何基函数，是一个有限次滤波的过程。这就使得EMD方法特别适用于非线性、非平稳信号的处理。因此，本文利用EMD方法对高速工况非平稳车内噪声信号进行平稳化处理。

采集信号经过EMD分解处理，得到有限个相对稳定的IMF分量，各个分量包含了原信号的不同时间尺度和特征信号，与原信号相比，具有更强的平稳性和规律性。EMD分解得到的信号分量必须满足以下两个条件：

① 对于每一个IMF分量，必须满足过零点和局部极值点的个数必须相等或最多相差一个；

② 在任意时刻点，局部极大值点形成的包络(上包络线)和局部极小值点形成的包络(下包络线)，均值必须为0。

EMD具体分解过程如下：

(1) 首先获取()(待分析信号)中包含的所有局部极大值点和极小值点，然后利用三次样条插值函数分别连接极大值点和极小值点，从而拟合出信号的上下包络线。

经过上述筛选处理，残余分量代表着信号的平均趋势，表现出单调性，此时循环停止，原信号可以表示为

1.2 BP神经网络原理

BP神经网络是一种多层前馈神经网络[4]，其拓扑结构图如图1所示。一般该网络包含输入层、隐含层和输出层，本文中输入层有4个神经元，隐层神经元根据具体情况通过人为调节来确定最佳个数，输出层有一个神经元。网络权值和阈值调整采用输出层误差反向传播，使输出不断逼近期望值。

隐含层的输出为

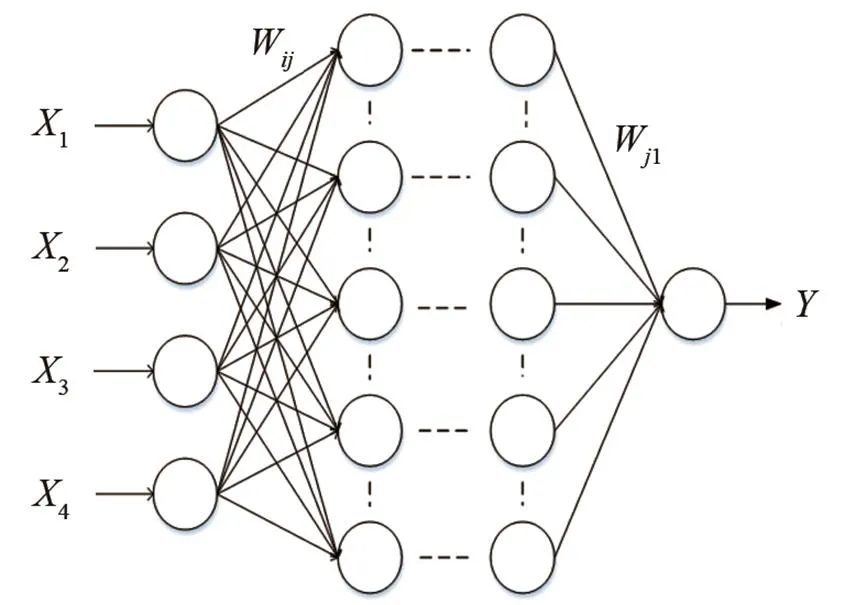
图l 典型的三层BP网络拓扑结构

现有理论已经证明，一个Sigmoid函数加上一个线性输出层能够逼近任意有理函数，但当Sigmoid函数进入饱和的目的区域时，会使网络的训练陷入饱和状态，大大降低了学习的效率。为解决这个问题，可选用双曲线函数。本文隐藏层采用的激励函数为双曲正切S形函数，值域范围为[-1,1]，表达式为

由于选用式(3)中的函数作为激励函数，所以训练数据必须进行归一化处理，采用线性转换算法将数据归一化到[-1,1]，公式为

BP神经网络的输出结果为

由此可计算网络的输出误差：

目前BP网络的应用十分广泛，发展也相对成熟，同时对时域信号具有良好的辨识与拟合能力。本文BP网络采用“有监督”的离线学习方式，为了准确地拟合噪声源信号与车内乘员耳侧噪声时域信号的规律，需要使用大量且全面的原始数据对其进行训练。

1.3 基于EMD和BP神经网络的重构算法

汽车高速行驶时，车内噪声信号声压变化具有随机性，采集的信号呈现非稳态、非线性的特点，从而导致BP神经网络对一些数据点的学习和训练存在混淆现象。基于现有的大多数方法在进行信号重构时，对于相对平稳的数据序列的重构精度很高，但是对于具有明显非平稳性的数据序列，由于其自身变化规律很难掌握，所以在进行重构时，重构精度一般比较低。因此，为了满足信号的重构精度要求，需要对信号进行平稳化处理。因为EMD分解方法可将非平稳数据序列分解成相对平稳的数据序列，因此，本文基于EMD和BP神经网络相结合的方法，对车内乘员耳侧噪声的时域信号进行重构。

在本文中，应用EMD分解，对各原始噪声时域信号进行分解，得到有限个固有模态分量(IMF)和趋势项。然而由于每个源信号数据非平稳程度不同，导致信号IMF分量的个数也不尽相同，如果利用各个信号的分解分量建立重构模型，势必会增大重构模型的建立难度，并且每个分量重构结果都会产生误差，误差的累加会增大重构结果的总误差。因此，按照信号分量自身不同的波动程度对其进行重新划分，得到重构后的分量，使其不仅包含原信号的所有特征信息，而且排除各分量之间的影响，这样即降低了建模难度，又提高了重构精度。

由于信号分量自身是以0为轴上下波动的时间数据序列，整体未呈现明显上升或下降的趋势，它的局部极大值和极小值点，在很大程度上反映了一个IMF分量的波动程度。因此，本文采用极值划分法对EMD分解得到的信号分量按波动程度进行重新分类，完成对所有噪声原信号分量的极值点个数的获取。

利用所获取的极值点个数，按频率对每一个原信号的IMF分量进行重新划分，进而获得高频、中频、低频3个分量。以这3个分量数据作为输入数据，乘员耳侧信号的3个分量数据作为期望输出值，对BP神经网络模型进行训练，通过调整隐层神经元的神经元数和训练次数，使网络误差满足工作要求，确定输入层、隐层和输出层的权系数以及各个节点的阈值，建立乘员耳侧的噪声信号相应频段的重构模型，将信号各频段的重构结果进行叠加，进而获得乘员耳侧噪声重构信号。算法流程如图2所示。

2 噪声源关键点选取

通过查阅相关文献[9-11]，初步确定车内噪声的主要贡献量在以下位置：轮胎，左、右A柱底端，左右A柱顶端，左、右后视镜，进、排气口。利用实车试验，采集以上位置测点的噪声时域信号，并在车外噪声源测点的麦克风上加装风球，麦克风采用逆风向布置，来减弱高速气流对测量过程的影响，如图3所示。

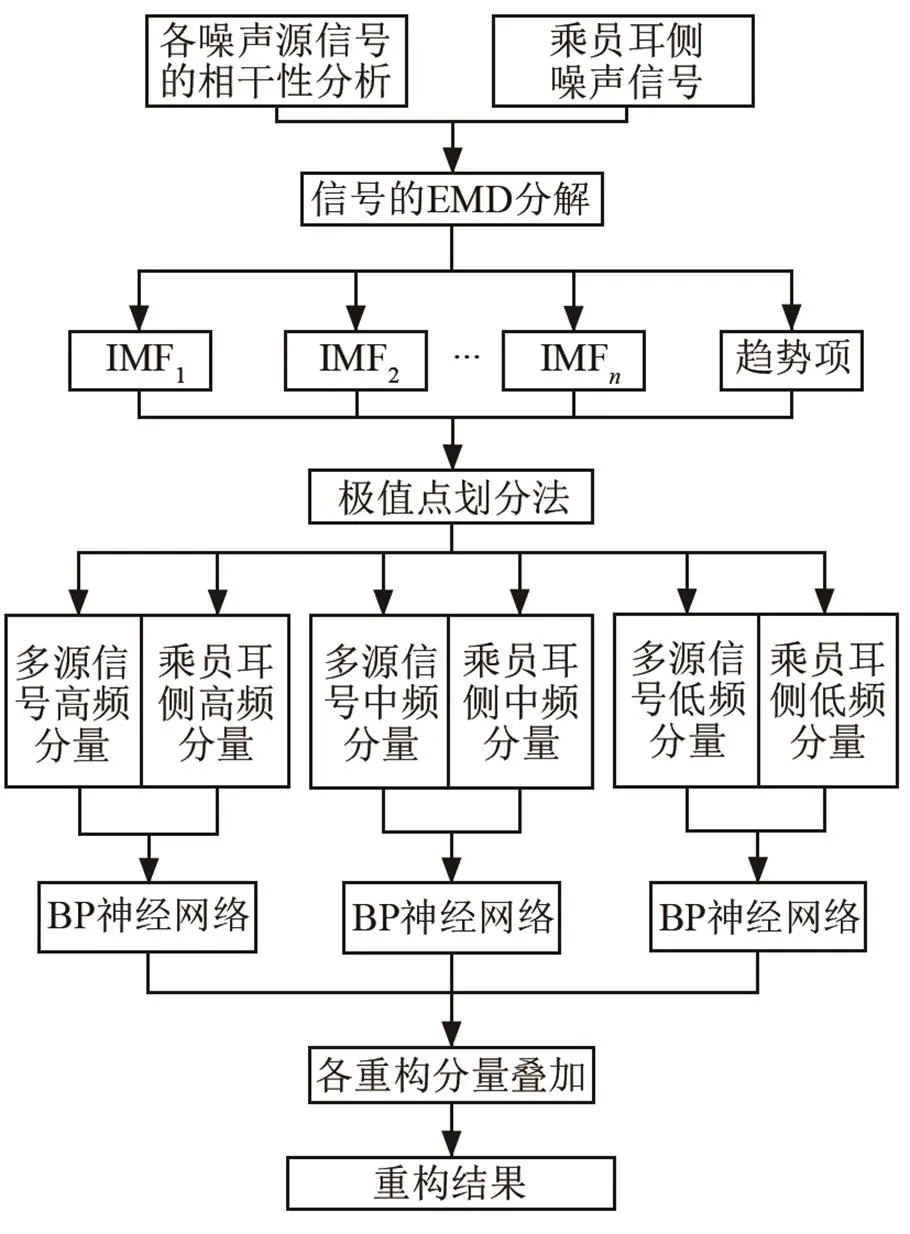
图2 基于EMD-BP的信号重构流程图

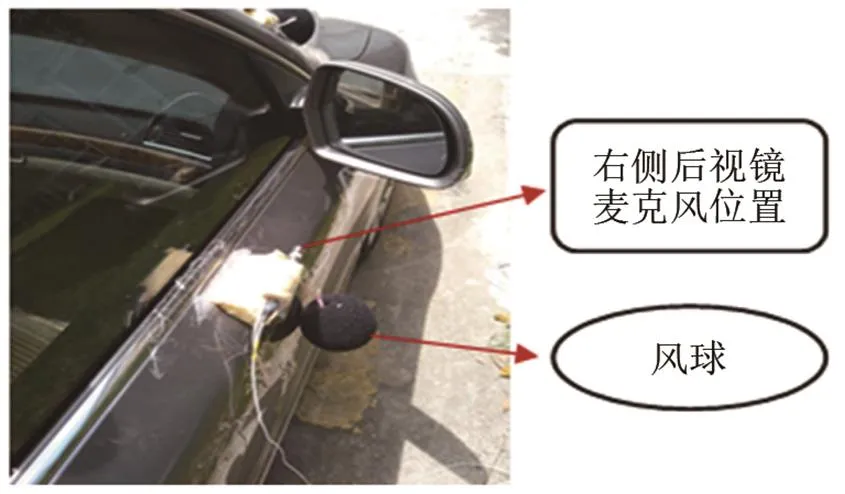
图3 右侧后视镜布点位置

在半消声室内，基于互易法[12]获取各传递路径的声-声传递函数，利用声学传递函数(Transfer Path Analysis, TPA)贡献量分析方法，选择最具有相关性的关键测点信号来重构车内噪声，重构公式如式(7)所示：

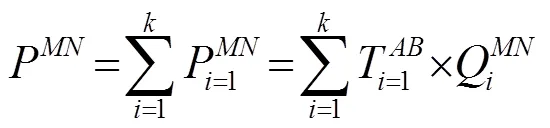
基于所测得的各测点位置到驾驶员右耳位置路径的传递函数，利用实际工况下测得的各测点位置的近场声压向量，由式(7)即可求得各测点对目标点的声压贡献量。以某轿车为例，其声压贡献量结果如图4所示，通过分析可知，源信号具有很强的对称性，进、排气口的贡献量明显低于其他位置，因此最终确定左A柱底端、左侧A柱顶端、左前轮、左后视镜以及乘员耳侧噪声信号作为噪声信号重构的关键点位置。

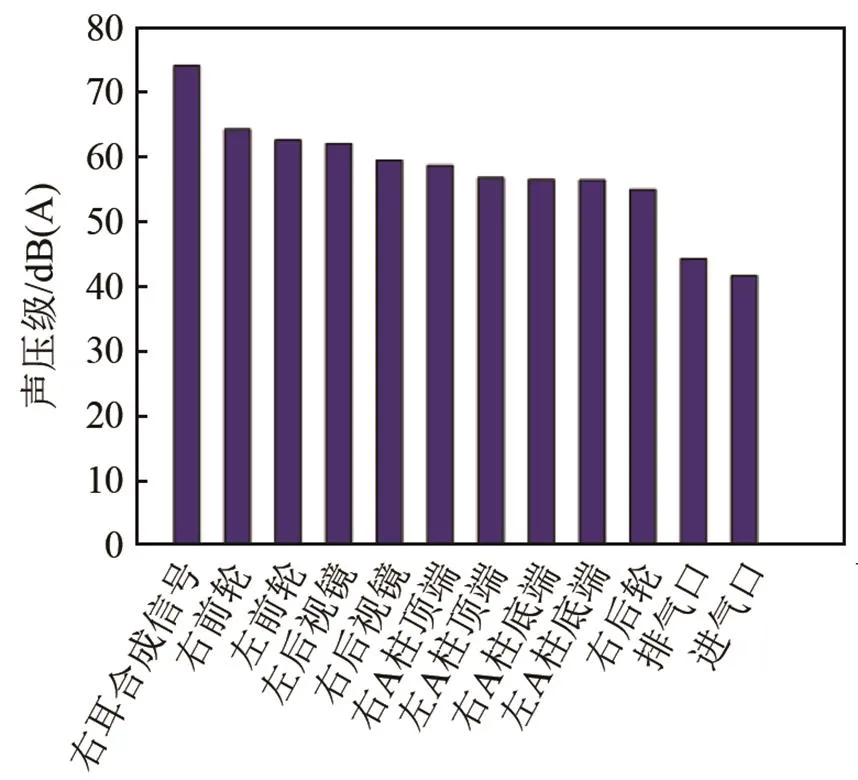
图4 各关键测点在高速下的噪声贡献量分析

3 试验验证

3.1 试验数据获取

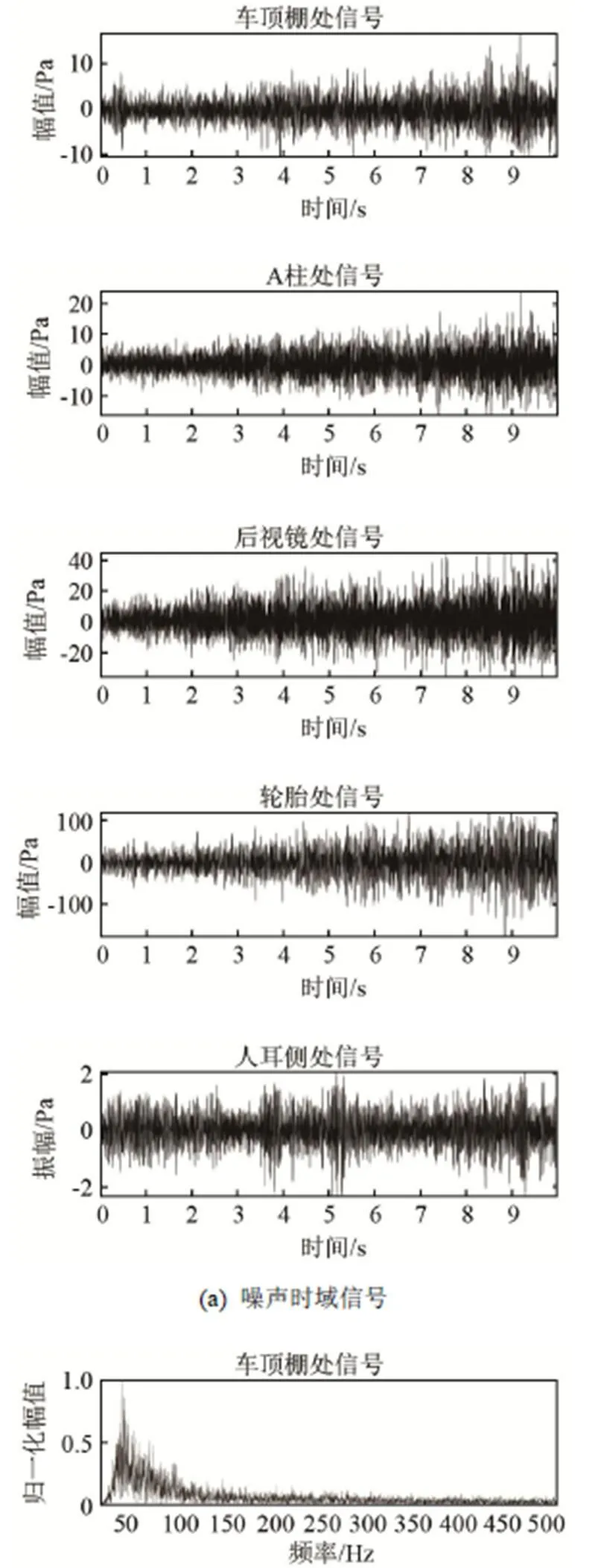
根据国标GB/T18697-2002[14]制定噪声信号采集方案，测试麦克风布置在驾驶员耳侧位置、左右A柱、左右后视镜、前后左右轮胎、车顶棚处，采集噪声信号，如图5所示，麦克风安装时尽量避免车辆震动。测试工况：匀速工况(车速80 km·h-1)、匀加速工况(车辆以80～120 km·h-1车速行驶)。测试车型：某轿车。测试仪器采用西门子公司的LMS数据采集器，采样频率为51 200 Hz，测试路面符合标准。测得两种工况下的数据，考虑到人耳听觉范围在20～20 000 Hz，需进行滤波处理。获取的乘员耳侧信号的频谱，如图6和图7所示。

图5 路试布点位置图

图6 匀速工况乘员耳侧噪声信号频谱

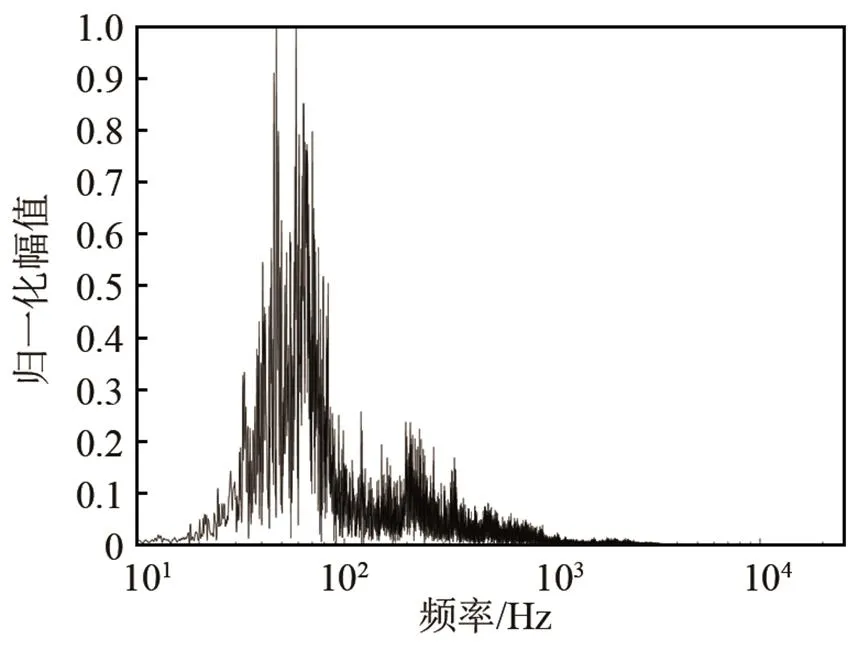
图7 匀加速工况乘员耳侧噪声信号频谱

从图6、7可以看出，车辆处于高速工况时，车内乘员耳侧噪声能量主要集中在中低频600Hz以下，在匀速工况下60 Hz左右频率段对耳侧噪声贡献最大，占主导地位，在200～500 Hz频率段有明显的小波峰；在匀加速工况下30～60 Hz频率段对车内噪声贡献最大，占主导地位，在200～500 Hz频率段有明显的小波峰。因此，对各原信号进行重新采样，只对频率在512 Hz以下的信号进行有效分析，采样频率为1 024 Hz，进行滤波预处理。预处理结果如图8、图9所示。

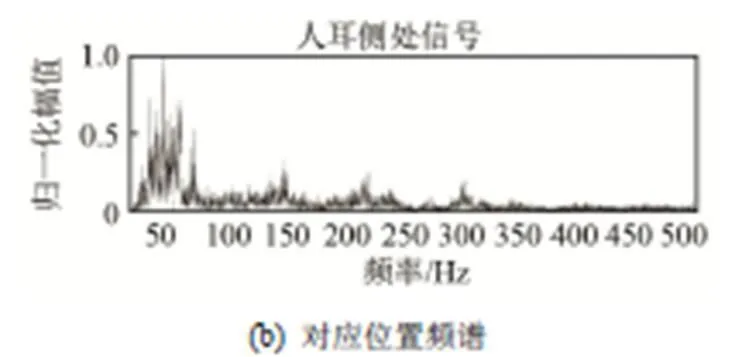
图8 匀速工况噪声信号及频谱

3.2 乘员耳侧噪声信号重构结果分析

为了验证本文提出的重构算法的有效性，选用匀速工况和匀加速工况进行案例分析，试验数据按照3.1节的方法进行数据预处理。利用重构模型根据实际测得的输入信号，分别对匀速工况及匀加速工况下车内乘员耳侧噪声的时域信号进行重构，结果如图10、11所示。

从图10(a)和11(a)中重构信号和实测信号的时域曲线对比可以看出，所提出模型的乘员耳侧噪声重构信号与实测信号在幅值和相位上有相同的变化趋势和较好的对应关系。结合图10(b)和11(b)中不同工况下的200 Hz以下的重构信号和实测信号的频谱对比分析可知，在整个频带范围内，重构信号和实测信号的波峰、波谷具有一致性，其幅值和相位有相同的变化趋势，其中在噪声的主要能量30～60 Hz范围内，其幅值和相位具有很好的对应关系，在频带60～200 Hz范围内，依然保持着较好的对应关系。因此，可以表明本文所提出的的EMD-BP神经网络重构算法在时域和频域上均具有较高的信号重构性能。

为了进一步分析重构信号的精度，本文采用平均相对误差来对其进行定量评价，如式(8)所示：

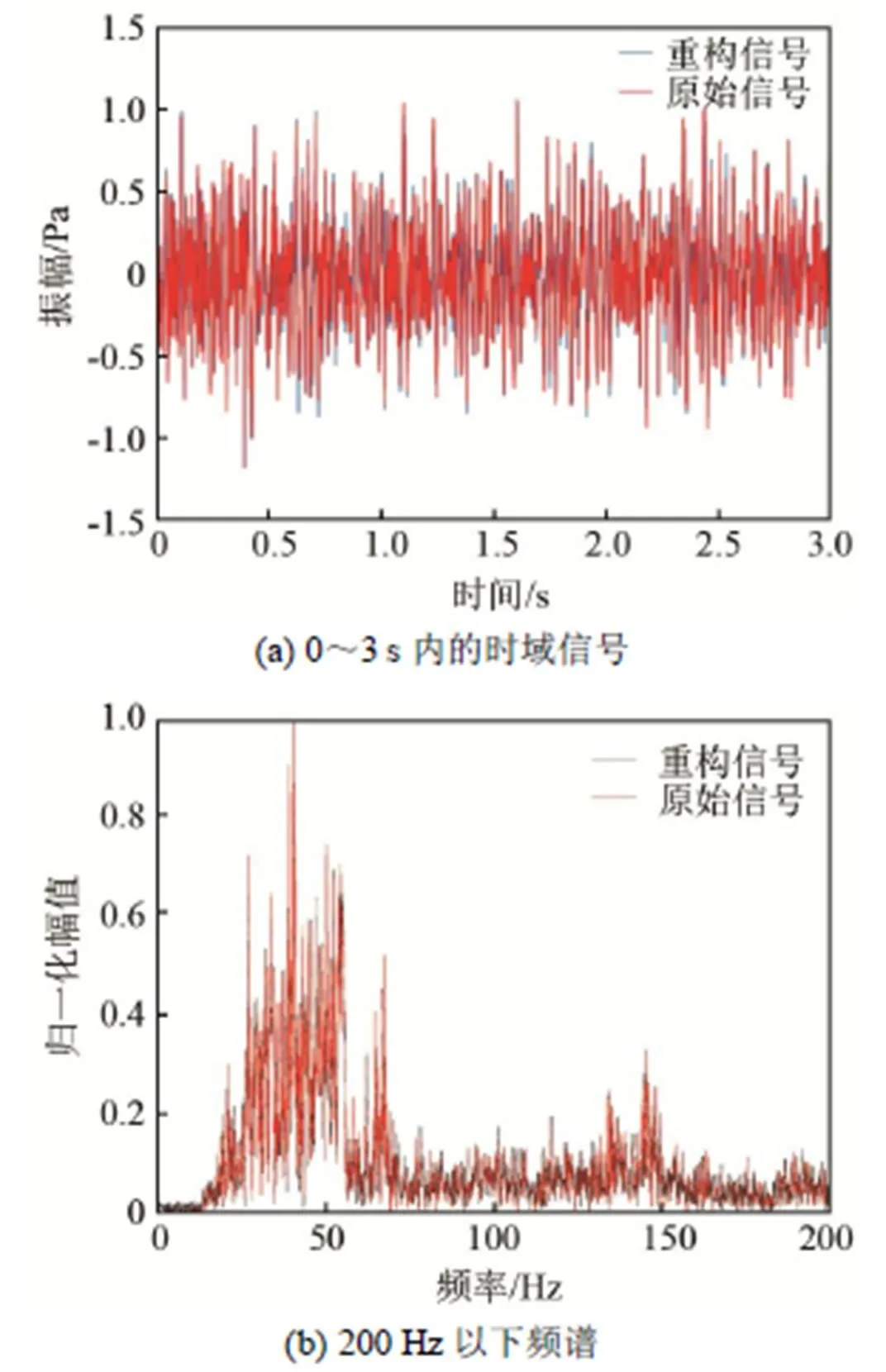
图10 匀速工况下重构信号与原始信号对比

将归一化结果代入式(8)中，得到不同工况下重构信号的平均相对误差，如表1所示。

表1 不同工况下的误差分析

从表1中可以看出，本文提出的算法，在匀速工况下的车内乘员耳侧噪声重构信号与原噪声信号的平均相对误差为0.222%，而在匀加速工况下重构结果的平均相对误差为0.324%，稍有下降。下降的原因主要是由于汽车在非稳态工况下运行时，车内噪声远比在稳态工况下复杂得多。但本文提出算法的重构结果的平均相对误差，均未超过1%[13]，这说明依据本文提出的模型对车内乘员耳侧噪声的信号重构的精度得到了很大提高。

综上分析可以看出，本文提出的EMD-BP神经网络重构算法，无论是重构信号的幅值和相位，还是重构信号的精度，均表现出了较好的性能。

4 结论

根据高速工况下，噪声信号具有非平稳性、非线性的特点，且风噪声、轮胎噪声是车内噪声主要的影响因素。因此，本文提出了一种基于EMD分解和BP神经网络算法的乘员耳侧噪声信号重构模型，并通过实车试验对算法的有效性进行了验证，结果表明：

(1) 对原信号进行贡献量分析、选取关键点信号，进行EMD分解，得到相对平稳的IMF分量，再对分量进行重构，这样不仅可以在很大程度上减少采样数据量，而且降低了信号的波动性对重构精度的影响。

(2) 利用极值点划分法，对IMF分量进行重新划分，得到3个特征信息比较集中且相对平稳的分量，然后对这3个分量进行神经网络数据融合，最后得到重构信号，这样不仅降低了建模的难度，而且减小了重构的误差。

(3) 本文提出的乘员耳侧噪声重构模型，可以实现高速工况下乘员耳侧噪声的信号重构，同时可以达到较好的重构精度。

[1] HUANG N E, SHEN Z, LONG S, et al. The empirical mode de- comosition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A, 1998, 454(3): 903-995.

[2] HALD J. Patch near-field acoustical holography using a new statistically optimal method[C]//Inter-Noise 03, Jeju (Korea), 2003: 2203-2210.

[3] NICOLAS P V, WILLIAMS E G, PETER C H. Equivalent sources method for supersonic intensity of arbitrarily shaped geometries[J]. Journal of Sound and Vibration, 2015, 347(5): 46-62.

[4] KWON H S, KIM Y H. Moving frame technique for planar acoustic holography[J]. J. Acoust. Soc. Am., 1998, 103(4): 1734-1741.

[5] 常振臣. 基于神经网络的车内噪声自适应有源控制系统仿真与试验研究[D]. 长春: 吉林大学, 2003.

CHANG Zhenchen. Simulation and experiment research on adaptive active noise control of automotive cabin based on network method[D]. Changchun: Jilin University, 2003.

[6] 常振臣, 王登峰, 周淑辉, 等. 神经网络方法在车内噪声信号预测中的应用[J]. 农业机械报, 2003, 34(1): 21-24.

CHANG Zhenchen, WANG Dengfeng, ZHOU Shuhui, et al. Application of neural network method to signal forecast of vehicle interior noise[J]. Acta Automatic Mechanics, 2003, 34 (1): 21-24.

[7] 苏丽俐. 车内声品质主客观评价与控制方法研究[D]. 长春: 吉林大学, 2012.

SU Lili. Research on vehicle interior sound quality subjective and objective evaluation and active control method[D]. Changchun: Jilin University, 2012.

[8] 曾庆山, 张晓楠. 基于EMD和组合模型的太阳黑子时间序列预测[J]. 郑州大学学报(工学版), 2014, 35(3): 78-81.

ZENG Qingshan, ZHANG Xiaonan. Sunspots time-series prediction based on EMD and combination model[J]. Journal of Zhengzhou University (Engineering Science), 2014, 35(3): 78-81.

[9] 刘旺林. 全频段车内噪声预测分析与控制研究[D]. 重庆: 重庆大学, 2016.

LIU Wanglin. Research on prediction and control of vehicle inner noise in full frequency band[D]. Chongqing: Chongqing University, 2016.

[10] JIA W, ZHANG T, DONG G, et al. Correlation analysis of car exterior and interior noise tests under different yaw angles with beamforming[C]//International Forum on Mechanical, Control and Automation, 2017.

[11] 薛昊强. 汽车车身壁板振动对乘坐室内噪声的声学贡献度分析研究[D]. 西安: 长安大学, 2015.

XUE Haoqiang. The vibration of each wall panel of the car on the indoor acoustic noise contribution analysis research[D]. Xi’an Chang’an University, 2015.

[12] 郭荣, 裘剡, 房怀庆, 等. 频域传递路径分析方法(TPA)的研究进展[J]. 振动与冲击, 2013, 32(13): 49-55.

GUO Rong, QIU Shan, FANG Huaiqing, et al. Advance in studying on transfer path analysis methods in frequency domain[J]. Journal of Vibration and Shock, 2013, 32(13): 49-55.

[13] 杨锡运, 孙宝君, 张新房, 等. 基于相似数据的支持向量机短期风速预测仿真研究[J]. 中国电机工程学报, 2012, 32(4): 35-41, 21.

YANG Xiyun, SUN Baojun, ZHANG Xinfang, et al. Short-term wind speed forecasting based on support vector machine with similar data[J]. Proceedings of the CSEE, 2012, 32(4): 35-41, 21.

[14] GB/T18697-2002: 声学, 汽车车内噪声测量方法, 2002.

GB/T18697-2002: Acoustics; measurement of noise inside motor vehicles, 2002.

The reconstruction method of occupants ear side noise under high speed condition

YANG Dong-po, WANG Xiao-lan, WANG Yan-song, GUO Hui, LIU Ning-ning

(School of Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China)

Vehicle interior noise signals have the characteristics of randomness and volatility under high speed condition. An algorithm based on Empirical Mode Decomposition (EMD) and BP neural network is applied to reconstructing the occupants’ ear side noise in this paper. Firstly, the critical noise source signal is determined by the analysis of the contributing to vehicle interior occupants’ ear side noise. Secondly, the selected noise source signal is decomposed into finite relatively stable IMF components by EMD decomposition. Then, the extreme point division method is adopted to divide the signals according to the fluctuation of each component, and the signal components are reconstructed into high frequency components, middle frequency components and lower frequency components. Finally, the corresponding BP neural network models are established for the signals in different frequency bands, and the reconstruction results in different frequency bands are superposed as the reconstruction result of the original signal. Based on five noise signal sources collected in a car, the noise signals in occupants’ ears side are reconstructed and the reconstruction results are analyzed. The results show that the noise reconstruction method proposed in this paper can realize the reconstruction of occupants’ ear side noise under high speed condition and has good performance.

high speed condition; vehicle interior noise; empirical mode decomposition (EMD); BP neural network; signal reconstruction

O422.8

A

1000-3630(2019)-03-0340-08

10.16300/j.cnki.1000-3630.2019.03.018

2018-01-20;

2018-03-04

国家自然科学基金(51675324、51175320)

杨东坡(1991－), 男, 河南商丘人, 硕士研究生, 研究方向为汽车噪声、振动和声振粗糙度。

王孝兰,E-mail: jlu_wangxiaolan@aliyun.com