小推力转移燃料消耗估计的机器学习方法

李海洋，宝音贺西

（清华大学航天航空学院，北京 100084）

引 言

电推进与传统的化学推进相比，具有比冲高、燃料质量消耗小等优点，探测器可以携带更多的有效载荷。美国的“黎明号”探测器、日本的“隼鸟号”探测器等都采用了电推进方式。在探测任务的初始设计阶段，往往有着大量的可选轨道设计方案，每一届的国际轨道竞赛（Global Trajectory Optimization Com‐petition，GTOC）和国内轨道竞赛的问题，任务设计期初需要求解复杂的全局优化问题。

小推力轨迹的设计与优化问题，相对于脉冲轨迹的设计与优化问题，求解较为困难，求解速度也较慢。由于计算能力与时间要求，不可能在全局优化的过程中对每一个方案都进行精确的小推力数值求解，这就需要对小推力转移进行快速准确的估计。最重要的是快速准确地估计小推力转移的燃料消耗。

考虑交会问题的燃料最优小推力转移。目前最为常用的估计方法，是用双脉冲转移Lambert问题的速度增量来近似估计小推力转移的速度增量，但是二者往往有着较大的误差。除此之外，Gatto 等提出了基于Edelbaum 近似的估计方法[1]，李海洋等同样基于Edelbaum 提出了考虑J2摄动下小推力多圈转移的估计方法[2]。

本文提出一种基于轨道根数特征的机器学习的估计方法。机器学习作为人工智能的一个研究领域，在轨迹优化领域也有应用[3-4]。Hennes等[5]研究了机器学习方法估计小推力燃料消耗，比较了不同的机器学习方法对估计结果的影响，但是在机器学习方法中，特征的选择对结果影响更为基础与重要，主要创新点是研究不同的特征组合对于估计结果的影响。

本文使用第7 届国际轨道竞赛的小天体数据[6]，生成小推力转移数据库供机器学习使用，选择不同的特征组合作为机器学习的特征，学习完成后即可对燃料最优小推力转移燃料消耗进行准确快递估计。不同的特征组合结果不同，但都明显优于Lambert 估计方法。

1 小推力转移数据库生成

1.1 Lambert估计

使用第7届国际轨道竞赛的小天体数据，随机选取出发天体A1和到达天体A2，在[0，3 000]天内随机确定出发时刻ts、在[100，300]天内随机确定转移时间Δt，在[0.5，1]×minitial内随机确定初始质量ms。燃料最优小推力问题较难求解，不可能每次随机生成的转移都可以采用小推力实现。所以，首先求解双脉冲Lambert 问题获得转移的速度增量，满足一定条件的转移再使用小推力实现。

若求解双脉冲Lambert 问题所得的速度增量为ΔVL，小推力能产生的最大推力为Tmax，如果满足下式

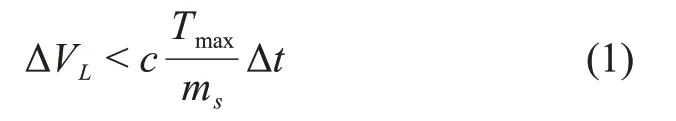
则认为该段转移可以转为小推力求解。式中c的范围一般取0.5～0.8之间，本文计算中取0.7。

Lambert估计的燃料消耗为

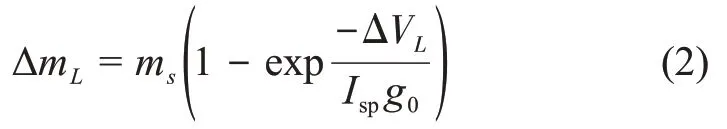
1.2 燃料最优小推力转移

经过双脉冲Lambert估计筛选后，可行的转移即可进行燃料最优小推力求解[7]。

探测器初末状态采用春分点轨道根数描述为

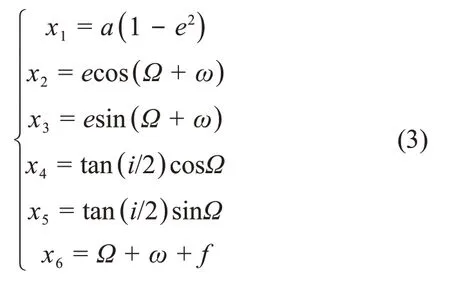
则小推力问题的动力学方程为

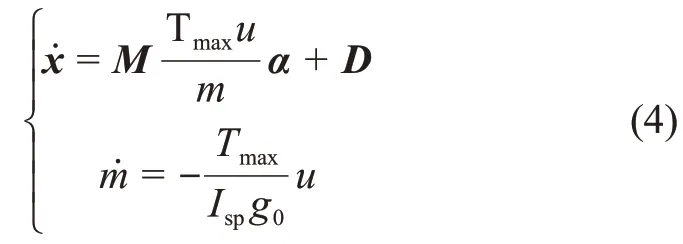
其中：M为 6×3 的矩阵，未列元素为 0；D为 6×1 的向量。

对于交会问题，约束条件为

对于燃料最优问题，优化指标为

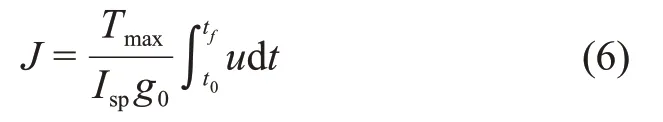
本文采用间接法求解燃料最优小推力问题。为了更加快速有效地求解协态变量初值，采用对数同伦方法与协态变量归一化技术[7]。

引入对数同伦参数ε和归一化协态变量λ0，指标函数变为

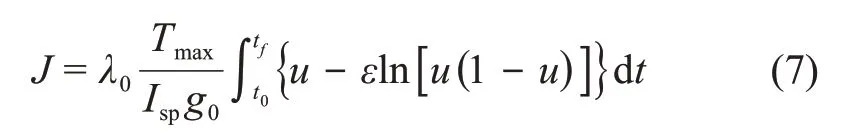
该最优控制问题的哈密顿函数为

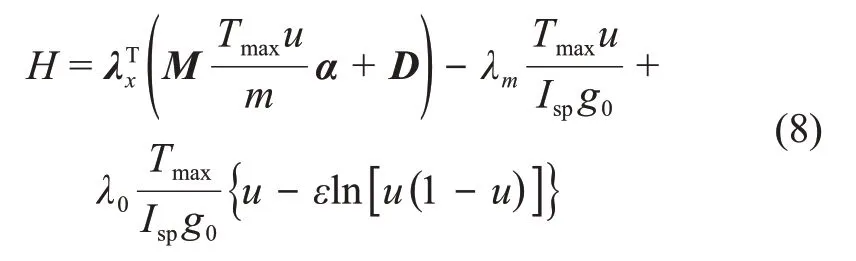
根据极大值原理，可以求得最优控制率为

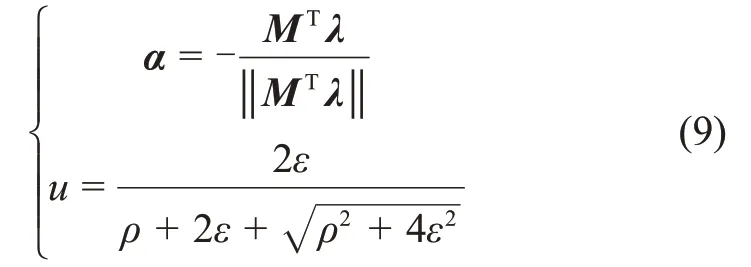
其中：开关函数ρ的表达式为

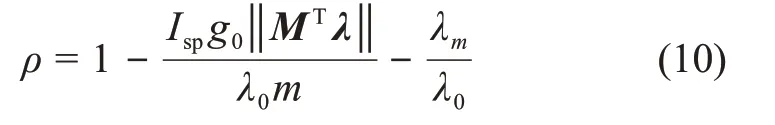
协态方程为

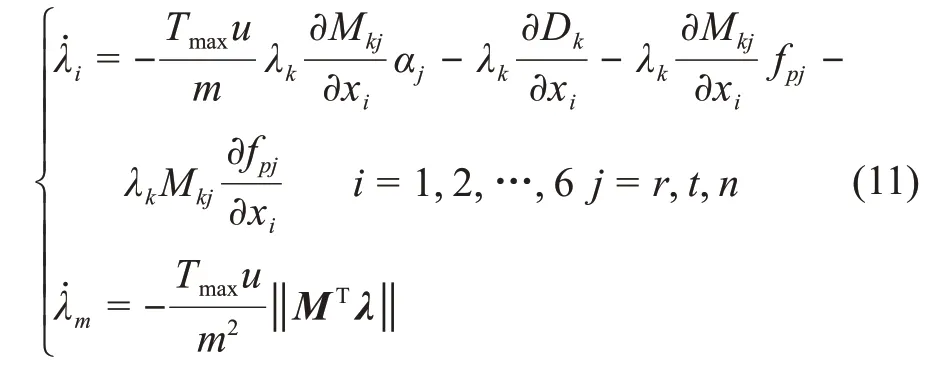
燃料最优小推力转移问题转换为求解协态变量初值的两点边值问题，可以使用打靶法求解。打靶方程为

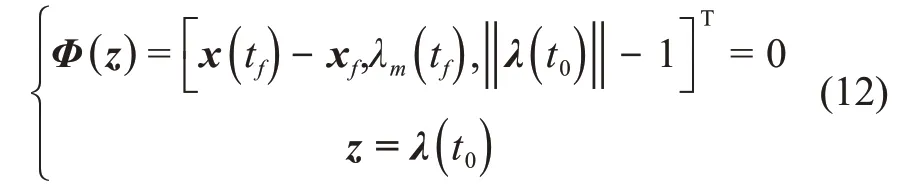
当同伦参数ε从1 减到0，问题即变为燃料最优问题。

2 机器学习方法

机器学习方法的本质可以理解为函数的拟合方法。对于燃料最优小推力转移问题，其燃料消耗是初末轨道参数、初始质量与转移时间的函数，但是该函数目前无法使用数学推导解析地获得准确形式。机器学习的过程则是构造拟合函数的过程，学习完成后构造的拟合函数可以用来描述相应的数学问题。

本文中的数学问题则是在二体太阳引力场中，给定小推力的最大推力和比冲，已知某组初末轨道参数、初始质量与转移时间，如何求解燃料消耗。只要满足该数学问题的场景，均可以采用本文得到的机器学习拟合函数进行燃料消耗估计，但是对于不同的场景，函数的拟合度可能不同，在实际使用过程中，还需要根据具体场景选择合适的学习数据。使用机器学习方法进行函数拟合的优势在于，机器学习方法对于复杂的函数关系可以有很好的描述，而解析公式必定会由于某些简化从而失去复杂函数关系的某些特性。机器学习有着较为成熟的工具包，本文计算采用Py‐thon 语言的 scikit-learn 工具包[7]，参考为文献[5]中得到的结论使用Gradient Boosting 回归器，最大深度选择为8。

根据第2 节的计算方法，一共生成6 万组燃料最优小推力转移，每组转移中包含了初末轨道参数、转移时间、初始质量和燃料消耗，其中，初末轨道参数、转移时间、始质量是基本变量，燃料消耗是希望通过机器学习获得的拟合函数的函数值。其中5万组用来进行学习燃料最优小推力转移燃料消耗，其机器学习标签即为燃料消耗质量；1万组用来进行检验机器学习估计的燃料消耗与小推力精确计算得到的燃料消耗的差异。

机器学习最重要的是特征参数的选择。燃料最优的小推力转移中，燃料消耗质量由探测器初始质量、转移时间，初始位置速度和末端位置速度决定。表1参数可以作为机器学习的特征。

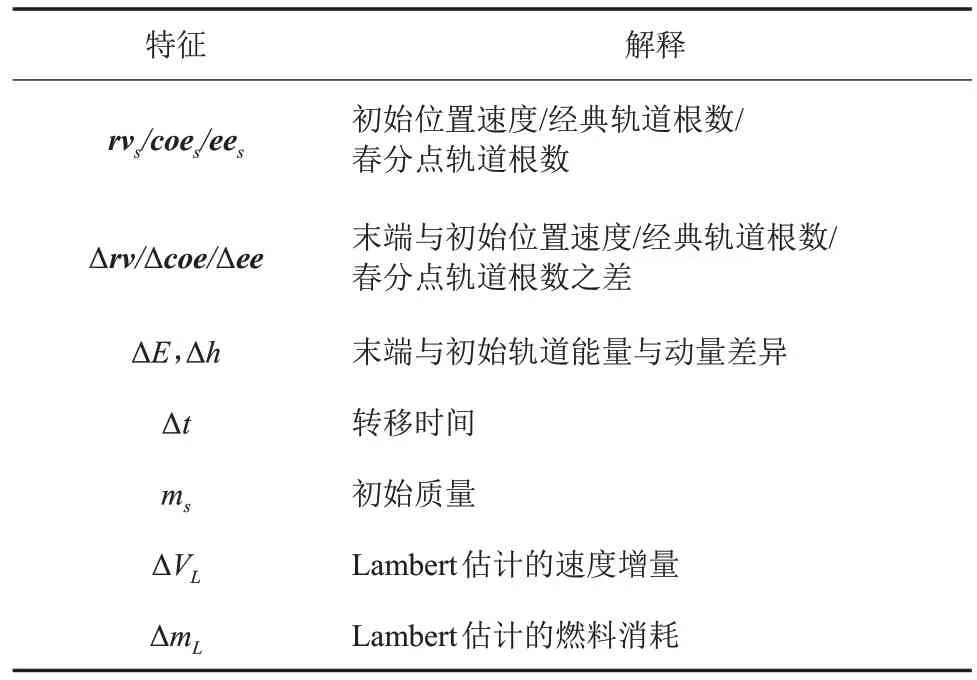
表1 可选特征Table 1 Possible attributes

本文选用表2中的7种特征组合进行分析，组合1表示的是利用位置速度的轨道描述方法作为特征，组合2表示的是利用经典轨道根数的轨道描述方法作为特征，组合3表示的是利用春分点轨道根数的轨道描述方法作为特征，组合4～6是在之前3组的基础上，再加上Lambert估计的速度增量和燃料消耗作为特征。组合7是在组合6的基础上考虑轨道积分中的能量与动量。

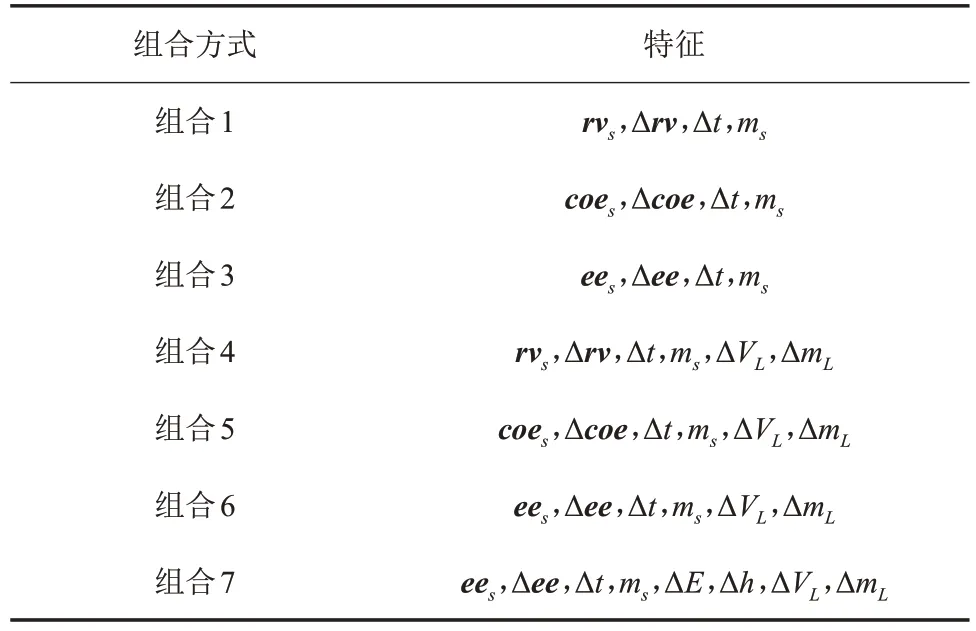
表2 6种特征组合Table 2 Six combinations of features

为了更为清楚地判断估计结果是否准确，采用估计燃料消耗与实际燃料消耗的均方差和均方根差作为估计精度的衡量标准。

3 算 例

本文使用第7届国际轨道竞赛的小天体数据，共16 256 个天体，轨道采用二体开普勒轨道，初始轨道根数的时刻为56 800MJD。探测器的初始质量为2 000 kg，小推力产生的最大推力为0.3 N，比冲为3 000 s。每组燃料最优小推力转移生成中，从16 256个天体中随机选取出发天体和到达天体，再随机确定出发时刻，转移时间和初始质量，根据第2节中的方法判断并生成小推力转移。使用该方法共生成6万组数据，其中1万组用来检验估计结果的小推力转移轨迹信息如表3所示。

下面对Lambert 估计和6 种特征组合方式的机器学习结果进行分析，结果如表4。

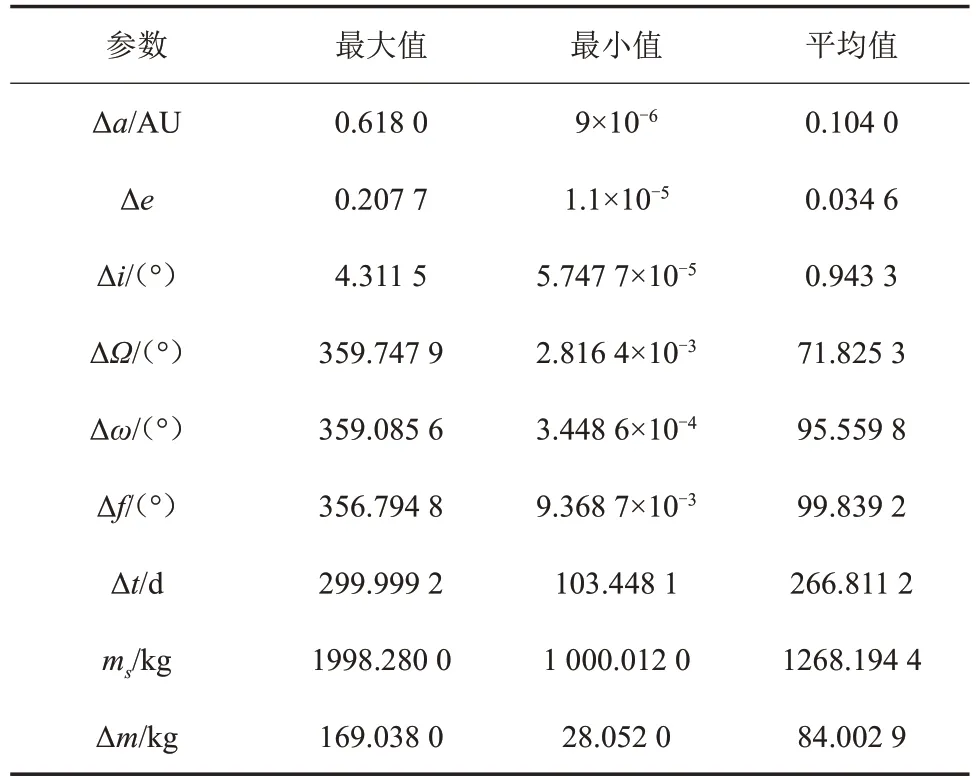
表3 小推力转移轨迹信息Table 3 Information of low-thrust transfers

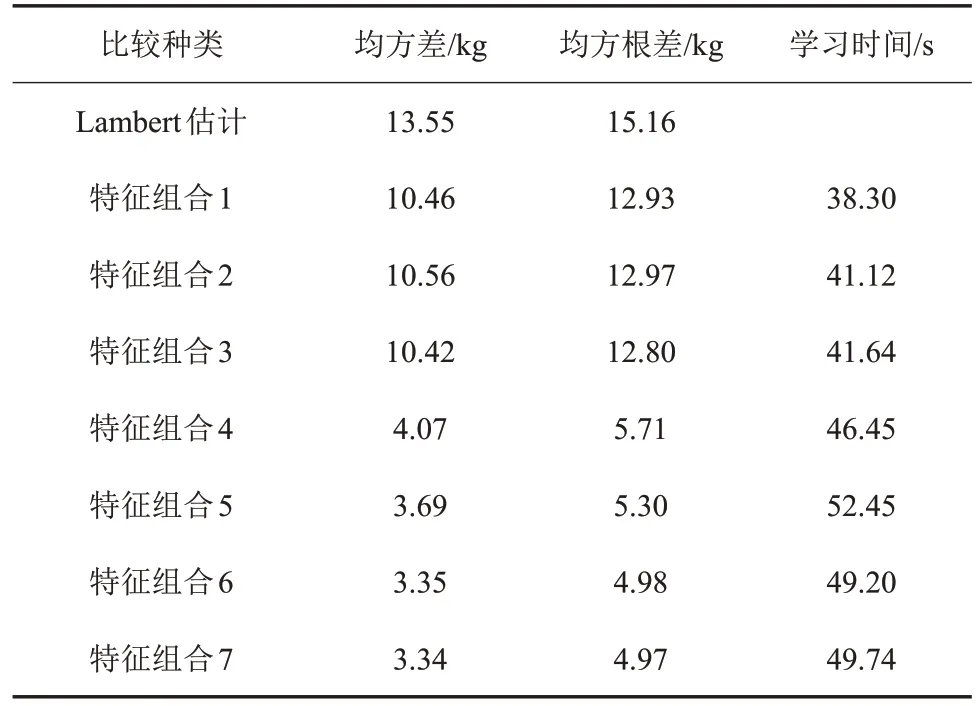
表4 估计结果比较Table 4 Estimation results

综合来看，燃料最优小推力转移燃料消耗机器学习估计方法明显优于Lambert估计方法。机器学习估计方法中，带有Lambert估计的速度增量和燃料消耗作为学习特征的特征组合明显更优。组合1、2、3的特征是构建一段小推力转移所需要的最基本的参数，但是作为机器学习的特征，为了得到更准确的估计结果，这些基本参数还需要额外信息，比如Lambert估计的结果。

对于机器学习方法来说，Lambert 估计的结果提供了一个学习的方向，使得机器可以在Lambert估计结果的基础上，更加快速准确地逼近真实值；而对于没有Lambert估计结果的特征组合，机器在学习过程中完全凭借转移所需的最基本参数，可能需要耗费更多的精力去学习，学习效果也相对较差。

对于不同的轨道描述方法，无Lambert估计特征的特征组合结果非常接近，有Lambert估计特征的特征组合中，春分点轨道根数的估计结果最优，经典轨道根数的估计结果次优。机器学习最重要的是特征参数的选择，特征的选择决定了机器学习到的是问题的表面还是本质。轨道根数的描述方法，相比于位置速度表示法，更能体现出轨道的本质属性，轨道根数表示法更能够直接表现出2个轨道的差异，所以通过轨道根数学习得到的结果要明显优于通过位置速度学习得到的结果。春分点轨道根数相比于经典轨道根数无奇异，更适合于小倾角近圆轨道，而本文使用的数据库中小天体多为小倾角近圆轨道，故结果最优。二体轨道中轨道积分应该是最能够反映轨道本质的参数，但是在本文中考虑轨道积分后的结果并无明显改观，仍然需要进一步进行探究。

特征组合3和特征组合6的误差分布图如图1～2所示，图1中横坐标为机器学习估计值与实际值的误差，纵坐标为个数，蓝色表示机器学习估计结果，橘红色表示Lambert 估计结果。图1中特征组合3 的机器学习结果误差虽然平均值接近0，但是Lambert 估计的误差分布更为集中，图2中特征组合6的机器学习结果具有更优的误差平均值和集中程度。

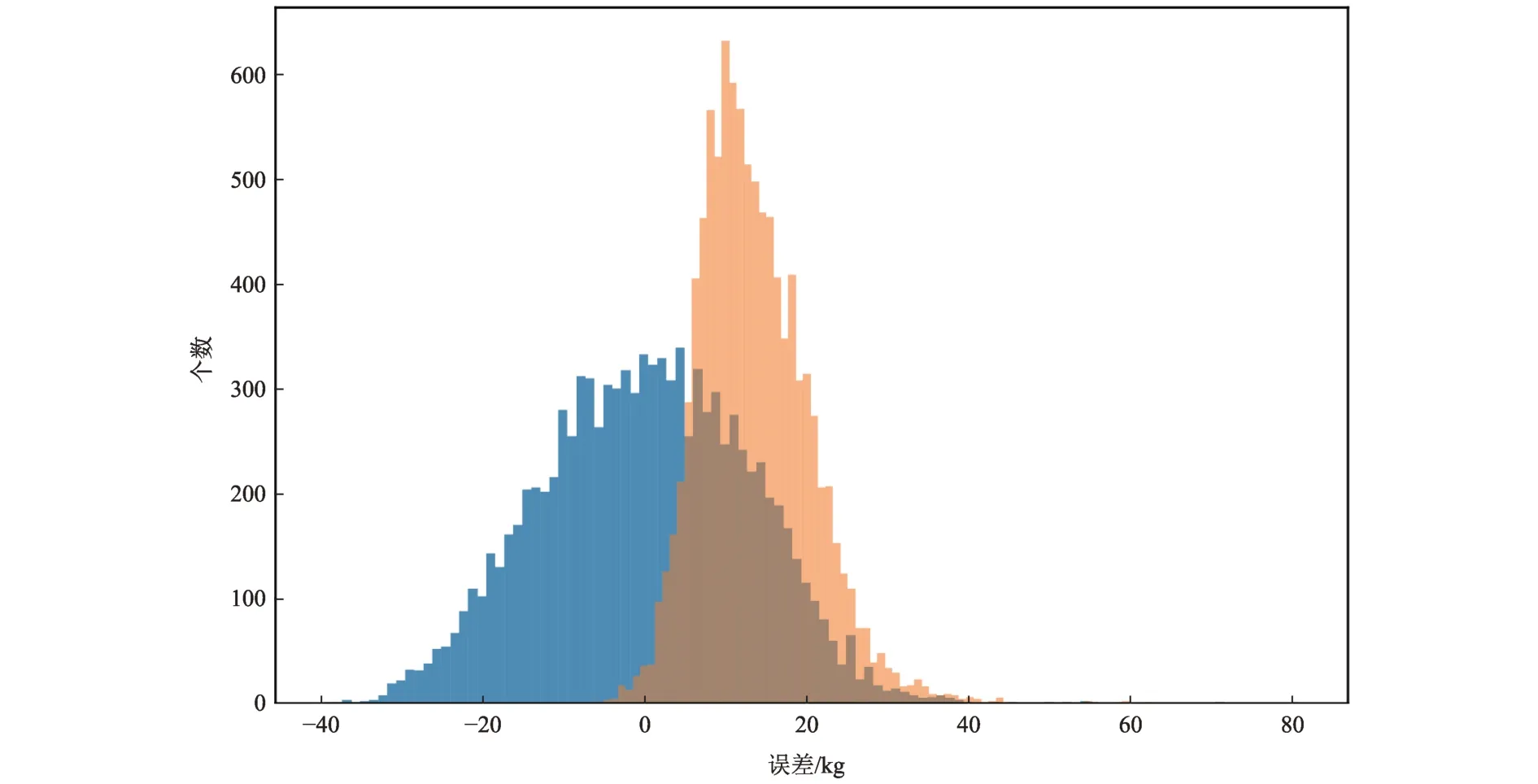
图1 特征组合3的误差分布Fig.1 Error distribution of Features III

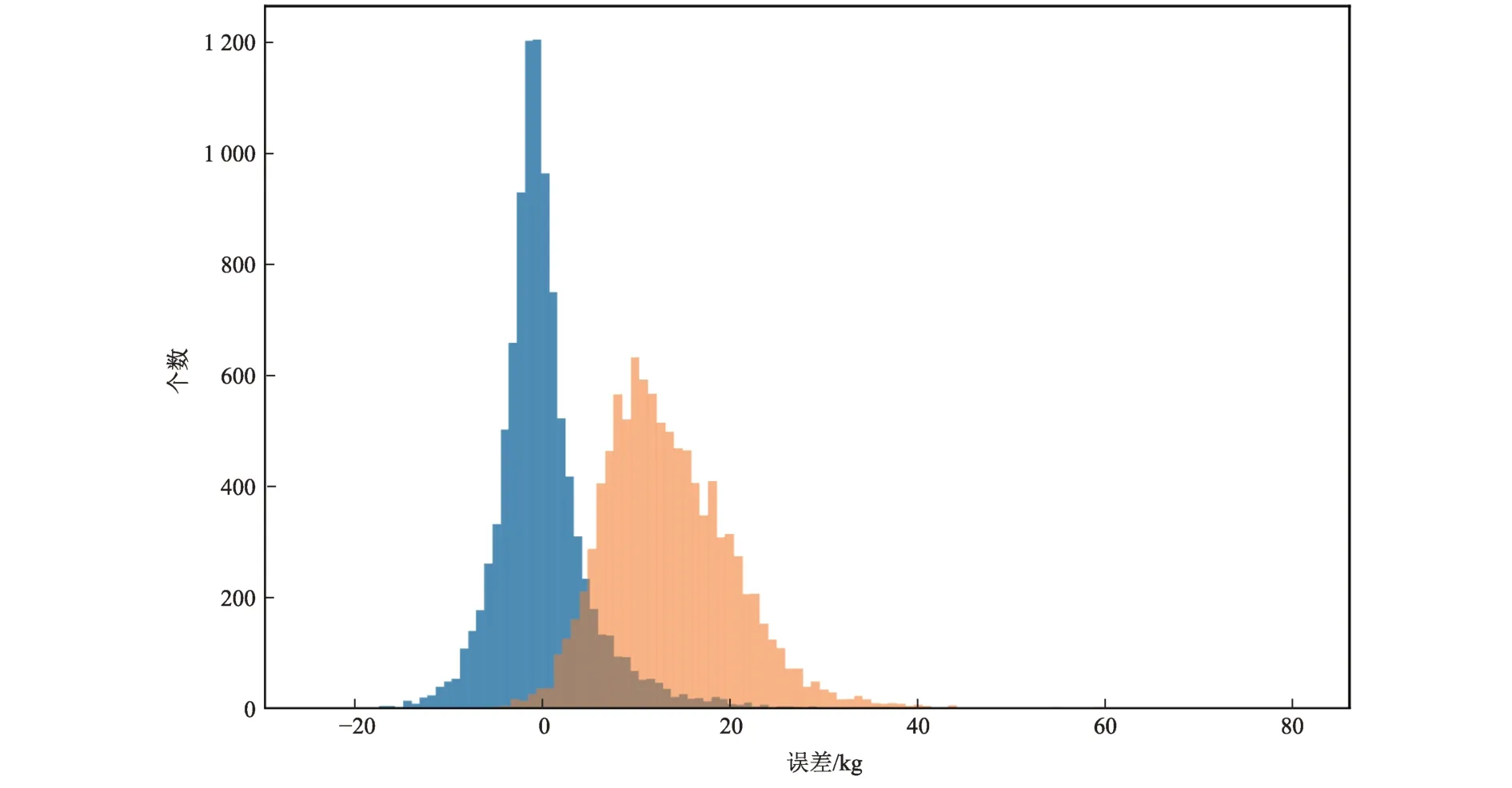
图2 特征组合6的误差分布Fig.2 Error distribution of features VI

4 结 论

本文采用机器学习的方法对燃料最优小推力转移的燃料消耗进行估计，比目前最为常用的Lambert估计方法结果明显更优。不同的特征组合会影响机器学习的结果。相比于初末轨道、初始质量与转移时间的特征组合，增加了Lambert估计结果的特征组合估计结果更优。在位置速度、经典轨道根数、春分点轨道根数3种轨道描述方法中，春分点轨道根数描述方法作为特征的机器学习估计结果最为准确。故带有Lambert 估计特征的春分点轨道根数的特征组合为较好的机器学习特征组合。

本文只考虑了不同特征对估计结果的影响，不同的机器学习算法与轨道描述方法之间的关联同样也会对估计结果产生影响，未来可以考虑研究使用更为准确的特征组合，以及不同的机器学习算法进行估计。