木星系探测及行星穿越任务轨迹初步设计

陈诗雨，杨洪伟，宝音贺西

（1.清华大学航天航空学院，北京 100084；2.南京航空航天大学航天学院，南京 210016）

引 言

1989年发射的木星探测器“伽利略号”，首次获得了木星大气的数据，并为木卫上存在地下海洋提供了有力证据[1-3]。近年来，人类再次将探索的目光投向木星，2011年发射的“朱诺号”木星探测器[4]现已环绕木星开展探测任务。此外，美国还计划发射“欧罗巴快船”探测可能存在地下海洋的“木卫2”[5]。在国外木星探测活动如火如荼展开之际，我国也在大力发展深空探测技术。“嫦娥1号”“嫦娥2号”“嫦娥3号”“嫦娥4号”任务的成功标志着我国在深空探测领域取得了重大突破，更长远的深空探测任务也随之被提上日程，木星探测器可能将于2029—2032年间发射。

与月球、火星等探测目标不同，木星是巨大的气体行星，人们对其结构和成分了解甚少。木星是包含多颗卫星的行星系统，其某些卫星与行星大小相近，还可能存在水和有机物，探索木星及其行星系统对于研究太阳系的形成和演化以及寻找适合人类居住的星球都具有重要意义。因此，类木行星系具有更高的探测价值。

木星探测任务的轨道设计比较困难，主要难点在于木星轨道能量大，以现有的发射能力不足以使探测器直接进入目标轨道，必须利用行星借力[6]。确定借力行星序列后，需进一步设计借力飞行轨迹。探测器在太阳系内运动时，受到太阳中心引力以及太阳光压力和行星引力等摄动，考虑借力飞行的问题更加复杂。在轨迹的初步设计过程中，为了便于快速搜索和计算，通常采用圆锥曲线拼接法将问题简化。将借力过程即探测器在借力行星引力影响球内的轨迹与日心段轨迹分开考虑，分别在二体模型下计算轨迹然后拼接[7]。由于借力飞行时间与整段转移花费的时间相比很短，通常可认为借力过程在瞬间完成，从而可将借力等效为一个脉冲速度增量，即借力时刻航天器的位置与借力天体相同，而速度发生突变。基于上述圆锥曲线拼接法和脉冲等效模型，可对借力飞行轨迹进行初步设计。探测器到达木星被木星捕获的速度增量通常较大，可考虑利用木卫多次借力辅助捕获。

Sims 等[8-9]研究了V∞杠杆机动技术，在借力后探测器轨迹的近日点或远日点处施加脉冲，使得探测器轨迹的周期与借力行星运行周期成一定整数比。该方法可用于构造共振借力轨道。Demyan和Russell等[10]利用V∞杠杆机动技术通过木卫借力实现了木星捕获。

本文首先比较了3种可能的借力序列，综合考虑总速度增量和飞行时间，选择较优的序列。然后利用粒子群优化（Particle Swarm Optimization，PSO）算法对地球-木星转移借力轨迹进行优化，以得到的地球-木星转移轨迹为基础，进一步利用木星借力，设计了行星穿越探测器的木星-天王星转移轨迹。最后设计木星系内转移轨迹，利用木卫构造多次共振借力，实现低消耗捕获。

1 借力轨迹优化方法

1.1 借力过程数学模型

惯性坐标系中，在借力的瞬间，探测器的位置矢量r等于行星的位置矢量rPl，且在借力前后，认为探测器的位置不变，即

探测器到达行星影响球时，称相对行星的速度为进入双曲线无穷远速度（简称双曲线速度，也称为双曲线剩余速度或双曲线超越速度），有

其中：v-为借力前探测器的日心速度矢量；vPl为借力行星的日心速度矢量。

同样，探测器离开借力行星影响球时的速度为离开双曲线速度，记为则

其中：v+为借力后探测器的日心速度。

如果在借力过程中探测器不进行主动轨道机动，进入和离开的双曲线速度大小相同，满足

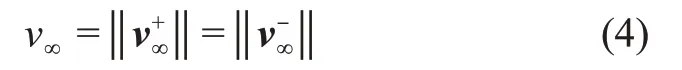
由于双曲线速度方向改变，探测器从借力中获得了速度增量为

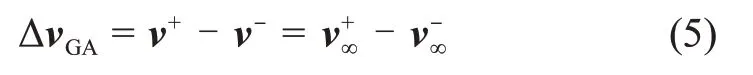
下面给出ΔvGA的表达式，以借力行星为中心建立坐标系P-ijk，如图1所示。

图1 借力坐标系Fig.1 Gravity assist frame of reference

i轴沿的方向，k轴为任意与i轴垂直的方向，这里取垂直于和vPl所构成的平面的方向，再选取j轴完成右手系的构造。三轴的单位矢量i、j和k表示为

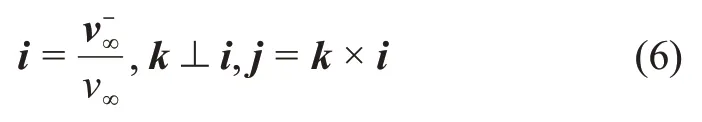
速度转角δ可由借力行星的引力常量μPl、双曲线速度大小v∞和双曲线轨道近星点半径rp（或称甩摆半径）计算

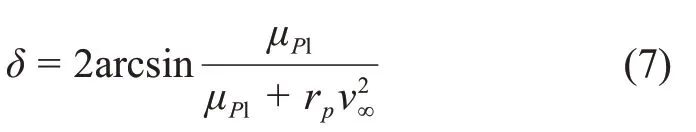
则ΔvGA可表示成

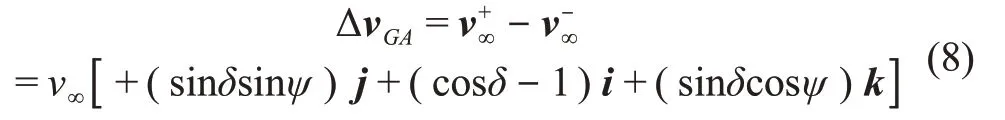
其中：角度ψ是在i-k平面上的投影与k轴的夹角，它的值可在[0，2π）之内自由选取。

在借力过程中探测器的双曲线轨道近星点半径不能小于事先设定的最小甩摆半径rpmin。探测器相对行星的双曲线速度偏转角δ不会超过最大偏转角δmax，最大偏转角δmax对应最小甩摆半径rpmin，即

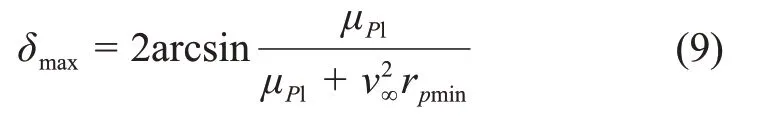
已知设计甩摆半径rp和角度ψ，就可以得到借力提供的速度增量ΔvGA和借力后探测器的双曲线剩余速度注意探测器以这里的离开该借力行星后不一定能到达下一颗借力行星或目标天体，往往需要施加深空机动进行轨道修正。

1.2 PSO优化算法

多次借力轨迹设计问题可转化为一个多变量的全局优化问题，通过对任务参数进行优化使得探测器所需提供的总速度增量最小。

假设探测器从地球出发，到达目标行星时，共经过N+1个行星（包括地球和目标行星在内），可以把整个任务分为N个阶段。

第1阶段：探测器t0时刻从地球出发，经过时间t1后到达行星1。查星历表读取t0时刻地球的日心位置和日心速度r0，v0以及t0+t1时刻行星1的日心位置和日心速度r1，v1，通过解Lambert问题求解发射时探测器的日心速度V0，到达行星1时的日心速度V11（第一个下标代表行星编号，第2个下标“1”代表飞行器进入该行星影响球，“2”代表飞行器飞出该行星影响球）；

第i+1阶段（i=1，2，…，N-1）：上一阶段已经求得t0+t1+…+ti时刻探测器到达行星i的日心速度Vi1以及该时刻行星i的日心位置和日心速度ri，vi。给定甩摆半径rpi以及角度参数ψi，即可求出探测器离开行星i的双曲线剩余速度，进而求得探测器离开行星i的日心速度Vi2。若不施加推力，则此时很难保证探测器能到达行星i+1，故需在行星i和行星i+1之间适当的位置施加深空脉冲机动ΔvTi。设施加深空机动的时刻为

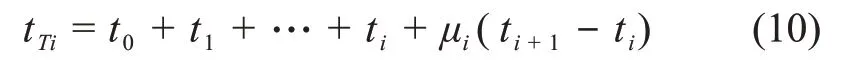
其中：μi为0到1之间的参数。

tTi之前的漂移段可由数值得到求出或轨道推演解析求出，从而获得tTi时刻探测器的日心位置和日心速度RTi，VT1i，查询星历表读取t0+t1+…+ti+ti+1时刻行星i+1的日心位置和日心速度ri+1，vi+1，通过解Lambert问题求解深空机动后探测器的日心速度VT2i，以及到达行星i+1时的日心速度Vi+1，1，则

整个任务执行期间所需的总速度增量大小为以上所有ΔvTi的总和。由以上过程可看出，ΔvTi是时间t0,t1,…tN-1t0，以及rpi、ψi和μi的函数（i=1，3，…，N-1），即

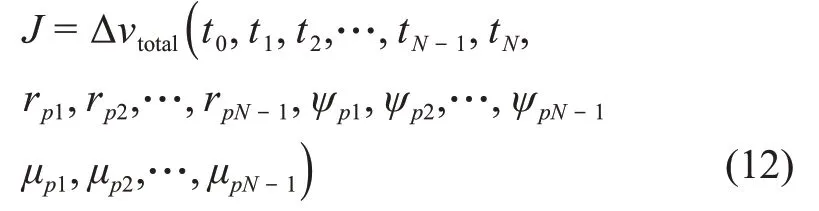
本文采用PSO，将以上参数作为优化变量，将总速度增量作为优化指标。实际任务中考虑到火箭发射能力有限，往往需限制发射C3能量，本文将发射C3能量约束在18km2/s2以内。在PSO算法执行过程中，若出现发射C3能量大于18km2/s2的解，则将优化指标的返回值置为108，从而该解被自动舍弃。

2 日心段轨迹设计

2.1 地球-木星段轨迹

对于木星探测任务，可选的借力行星有金星、地球、火星，文献[6]给出了金星-地球借力（VEGA）、金星-地球-火星借力（VEMGA）以及金星-地球-地球借力（VEEGA）3种可行的借力序列。本文用第2节所述方法，分别对这3 种借力序列的轨迹进行优化。发射窗口在2029年—2032年之间，地球-木星转移段飞行时间不超过7年。PSO算法的粒子个数设置为30，迭代次数为5 000次。每次借力的最小借力高度为200 km。对每一种借力序列，PSO 优化100 次，取其中最优解。优化结果如表1所示。

表1 三种借力序列轨迹优化结果对比Table 1 Comparison in the optimal trajectories for three gravity assist sequences

由表1可见，在选定的发射窗口范围及飞行时间上限等条件下，金星-地球借力序列所需总速度增量明显较小，因此地球-木星段转移轨迹采用该借力序列。转移轨迹的详细数据见表2，轨迹如图2所示。

图2 地球-木星段转移轨迹Fig.2 Earth-Jupiter transfer trajectory

2.2 木星-天王星段轨迹

行星穿越探测器由木星系探测器携带，并在到达木星时与其分离，分离前不提供速度增量。两者分离后，行星穿越探测器利用木星借力，然后直接飞往天王星，在2049年前实现天王星的飞越探测。根据地球-木星段轨迹的木星到达时刻及到达木星时的v∞，通过设计借力半径rp、角度参数ψ、深空机动时刻和天王星到达时刻，即可得到木星-天王星段转移轨迹。将上述几个参数作为优化变量，深空机动的脉冲大小作为优化指标，使用PSO优化得到的结果如表3所示。

表3 木星-天王星转移轨迹数据Table 3 Data of Jupiter-Uranus transfer trajectory

图3 行星穿越段转移轨迹Fig.3 Jupiter-Uranus transfer trajectory

3 木星系内转移轨迹设计

木星系探测器进入木星环绕轨道后，对木星及其卫星进行科学探测，并最终捕获至一颗卫星的环绕轨道上。由于“木卫4”上可能存在水和有机物，是木星系统中除“木卫2”外最有可能存在生命或适合生命居住的星球，且至今人类没有对“木卫4”进行环绕探测的任务计划，因此选择“木卫4”作为最终的环绕探测目标。

然而，探测器进入木星影响球时相对于木星的速度大小为v∞=6.230 km/s，若直接制动捕获则所需速度增量由式（13）估计。

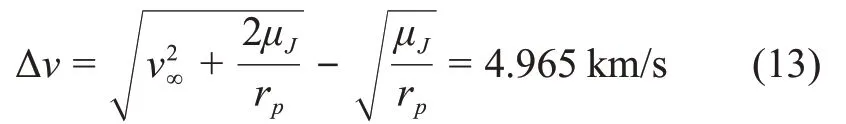
其中：μJ为木星引力常数；rp为“木卫4”轨道半径。

直接制动所需速度增量太大，因此需利用木星4颗较大的卫星“木卫1”到“木卫4”借力辅助捕获。“木卫3”是4颗木星卫星中质量最大的，利用其可提供的速度增量也最大，首先选择“木卫3”借力，将探测器捕获至环木大椭圆轨道上。在该大椭圆轨道的远木点处施加脉冲，抬高近木点的同时使探测器向“木卫4”转移，通过PSO优化到达“木卫4”的时间，使得远木点处施加的脉冲最小，该过程轨迹如图4所示。

图4 木星系捕获轨迹及“木卫3”-“木卫4”转移轨迹Fig.4 Jovian system capture trajectory and Ganymede-Callisto transfer trajectory

探测器到达“木卫4”后，利用“木卫4”构造共振借力使其轨道接近于“木卫4”的轨道。所谓共振借力就是探测器经天体借力后与借力天体的轨道周期成正数比，使得探测器在经历一定时间后再次利用该天体借力。共振借力轨道的构造方法如下，若已知探测器进入借力天体的双曲线剩余速度则知道了进入和离开双曲线剩余速度v∞。假设希望借力后探测器轨道周期为T，中心天体（木星系内中心天体为木星）引力常数为μ，借力时探测器与中心天体的距离为r，则可求出借力后探测器相对于中心天体的速度vout为

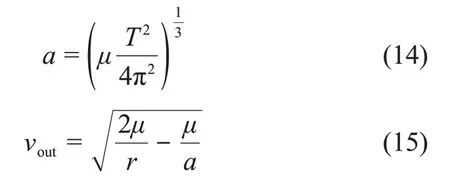
借力过程各速度矢量如图5所示，借力天体速度vp为已知量。x轴沿vp方向，z轴沿探测器相对于中心天体的角动量方向，y轴与x轴和z轴垂直。根据vp、v∞、vout的大小求出角度θ，并设计v∞在y-z平面的投影与y轴的夹角φ，使得出射速度vout所在的轨道平面与借力天体轨道平面夹角最小。通过以上步骤得到了的方向角θ与φ，即可求出的夹角δ，若δ不大于最大甩摆转角δmax，则该共振借力轨道构造完成，否则该共振借力轨道无法构造。

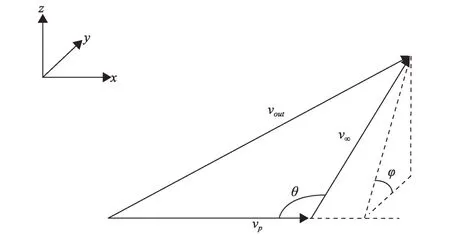
图5 借力过程速度矢量示意图Fig.5 Velocity vectors in gravity assist

通过上述方法构造7次“木卫4”共振借力，其中前4次共振轨道周期比依次为6、4、3、2，用于减小探测器轨道半长轴，后3次共振轨道周期比均为2，用于减小探测器轨道倾角，使探测器轨道与“木卫4”轨道基本在同一平面内。共振借力轨道如图6所示。

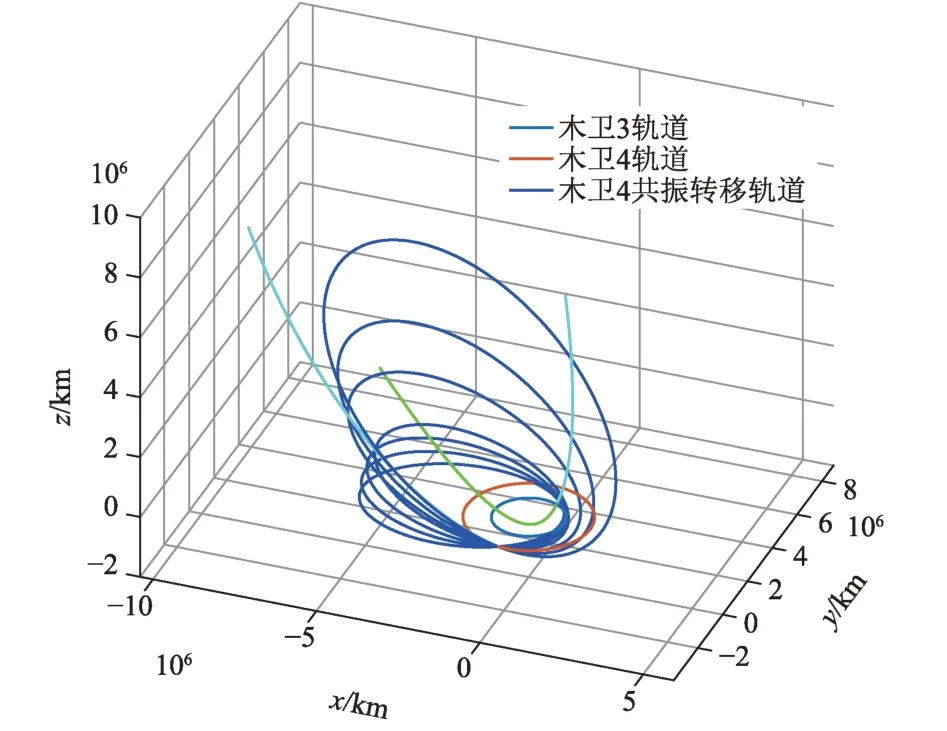
图6 木卫4共振借力轨道Fig.6 Trajectories with Callisto resonant gravity assist

共振轨道为了进一步减小轨道偏心率，探测器再次利用“木卫4”借力并施加深空机动，然后返回“木卫4”。该过程使用PSO进行优化，优化指标为

其中：ΔvT为深空机动大小；e为深空机动后探测器轨道偏心率；加权系数K取4.0。

探测器回到“木卫4”后，再次利用“木卫4”借力2次，每次借力后均施加一次深空机动，最后在“木卫4”附近制动，捕获到轨道高度为500 km 的环“木卫4”圆轨道上。该过程使用PSO优化，使得2次深空机动以及“木卫4”捕获时制动脉冲之和最小。整个木星系内转移轨迹如图7所示，相关数据见表4。从进入木星影响球到最终环绕木卫4共耗时约3.5年，整个木星系内转移轨迹消耗2.335 km/s 的速度增量，比直接制动捕获所需的速度增量大幅减少。结合地木转移轨迹和木星系内轨迹，木星系探测器需提供的总速度增量为3.042 km/s。

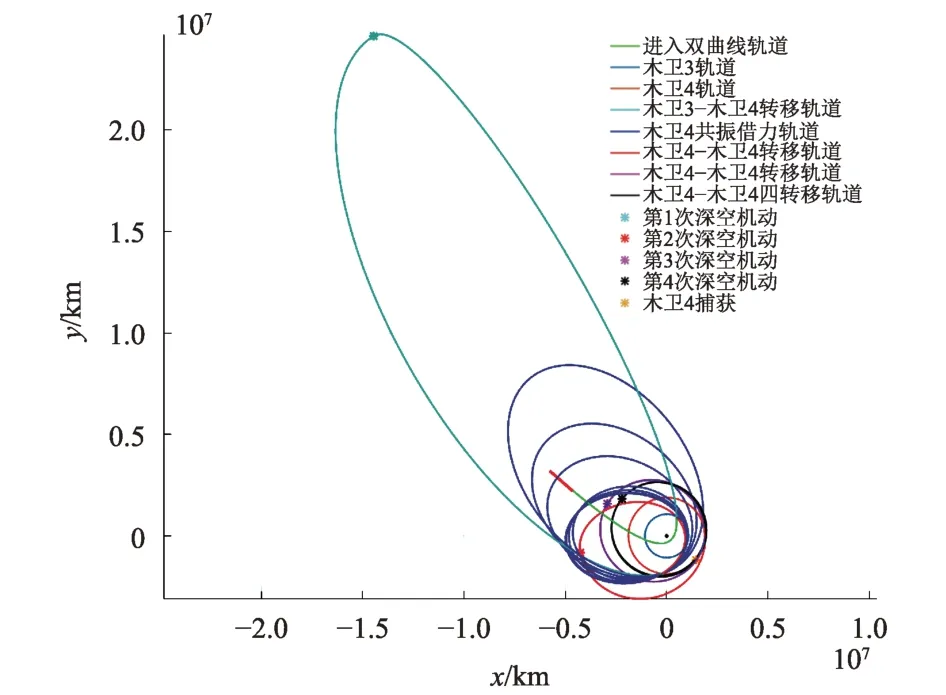
图7 木星系内转移轨迹Fig.7 Trajectories in Jovian system

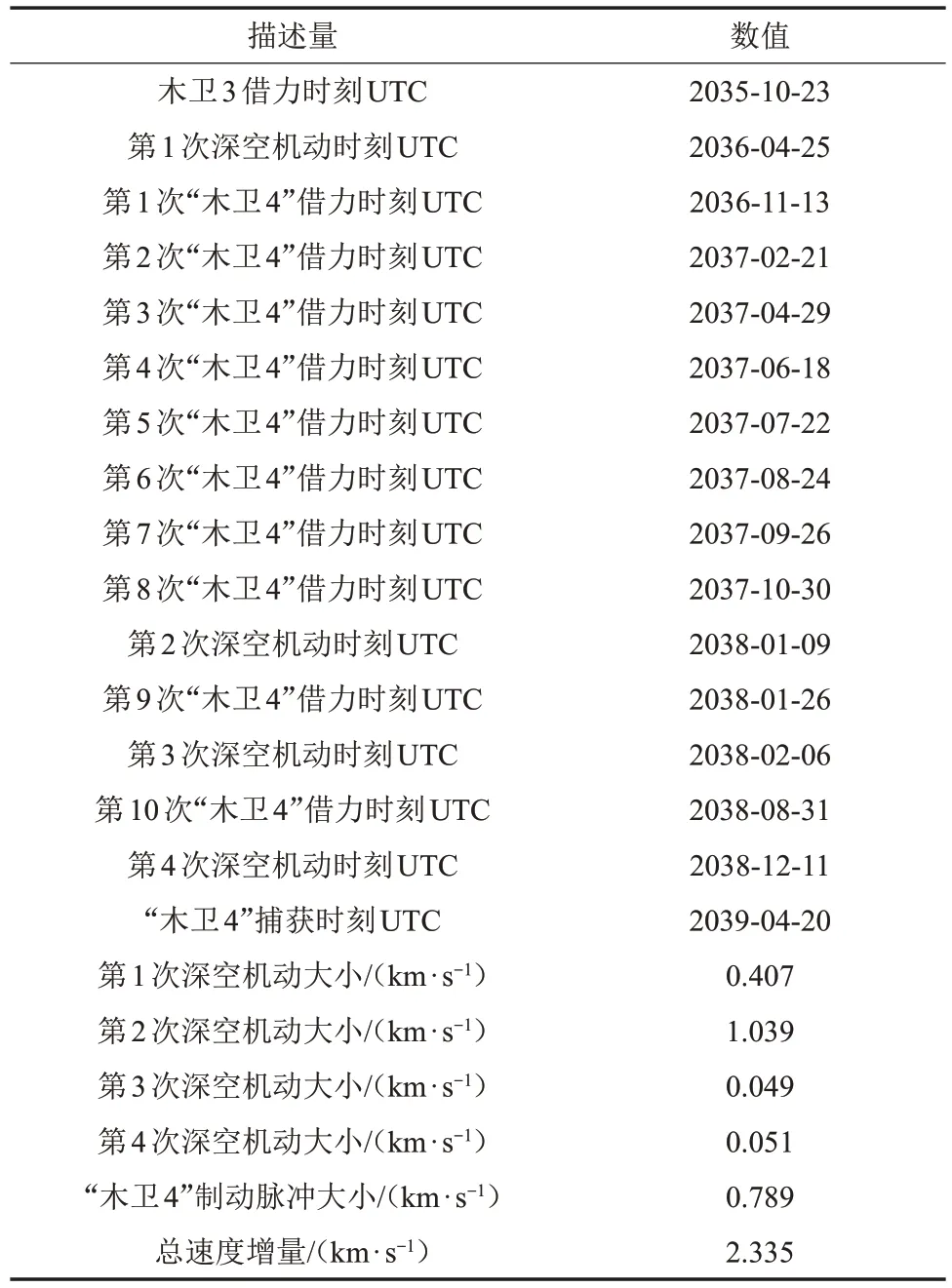
表4 木星系内轨道数据Table 4 Data of trajectories in Jovian system

4 结 论

本文使用PSO 算法，对木星系探测及行星穿越探测任务的轨迹进行优化。对于地球-木星段转移轨迹，在2029—2032年的发射窗口范围及7年的飞行时间上限约束下，金星-地球借力序列比金星-地球-地球和金星-地球-火星借力序列更节省燃料。木星系探测器通过木星卫星多次借力可有效地减小被木卫4捕获所需的速度增量，整个木星探测任务所需速度增量为3.042 km/s。行星穿越探测器在到达木星时与木星系探测器分离，随后通过木星借力可不耗费燃料直接飞往天王星，并于2043年完成天王星的飞越探测任务。