载人深空探测磁场主动辐射防护技术研究

蔡明辉，杨 涛，韩建伟

（1.中国科学院国家空间科学中心，北京 100190；2.中国科学院大学天文与空间科学学院，北京 100049）

引 言

高能宇宙线对航天员的辐射具有非常大的危害，是载人深空飞行必须面对也是亟待解决的一个重要问题。由于缺少庞大地球磁场的屏蔽作用，载人深空飞行中航天员遭遇的日均辐射剂量是近地空间站的3倍。2012—2013年，美国国家航空航天局（National Aeronautics and Space Administration，NASA）“好奇号”辐射评估探测器的探测结果表明：平均每天辐射剂量大约为1.84 mSv，而且95%的辐射剂量来源于银河宇宙线（Galactic Cosmic Rays，GCR）。因此，对于类似500天往返火星的长时间深空载人航天任务遭受的GCR辐射剂量高达940 mSv，如果遭遇偶发的太阳质子事件（Solar Proton Events，SPE）则可在短时间内达到1 000 mSv的辐射剂量。美国辐射防护与测量委员会规定，考虑到重离子辐射剂量的不确定性及空间辐射在导致癌症、中枢神经损伤、心血管疾病方面的不确定性，NASA 建议置信度为95%的情况下，辐射致癌风险小于3%的剂量限制是150 mSv[1]。因此，长时间的载人深空飞行中航天员遭遇的辐射风险非常高，必须寻找有效的辐射防护方法和技术。

银河宇宙线和太阳宇宙线粒子能量高达GeV/n，靠传统物质阻挡的被动屏蔽方式非常低效，迫切需要发展更加高效的主动屏蔽方法。目前，国际上正在积极探索的载人航天主动防护方法主要有静电场防护、等离子体防护和磁场防护[2-3]。静电防护基于静电场对带电粒子的作用原理，主要采用双球同心结构[5]或多球结构[4-5]，需要在防护区外安装体积较大的设备；等离子体防护[6]通过在防护区表面加上正电势以排斥质子和重离子，并在防护区周围建立弱磁场捕获电子阻碍其进入防护区；磁场防护[7]基于洛伦兹力对带电粒子的偏转使其无法到达防护区，分为约束磁场防护与非约束磁场防护。

早在1961年，美国空军司令部就提出利用超导线圈进行辐射防护的思路；1961—1969年间，NASA和美国空军开展了一系列使用超导强磁场进行主动防护的研究，但由于质量资源、超导技术等各种原因，磁场主动防护在工程上一直处于理论研究阶段；近10年来，随着高温超导（High Temperature Supercon‐ductor，HTS）技术的进步和新型磁场构型的提出使得磁场主动防护成为可能；2005年，美国麻省理工学院提出基于阿尔法磁谱仪超导磁体的魔环结构思想，将二极磁体轴向结构进一步拉长，形成具有封闭磁场的结构以便使宇航员免受空间高能粒子的辐射危害；2011年，欧空局提出2种双螺旋结构磁场屏蔽方案。2014年，NASA发布了最新的磁场主动防护技术报告（Magnet Architectures and Active Radiation Shielding Study，MAARS），系统论证了利用HTS 技术实现航天员主动防护的可行性和优势[8-13]。

综上所述，磁场主动屏蔽防护技术是未来深空探测与载人航天行星际飞行空间辐射防护的一个重要方向。本文将基于单粒子轨道理论和蒙特卡洛方法建立一种磁场主动屏蔽防护分析方法，开展磁场主动防护的机理和磁场结构设计，研究结果可为我国后续载人深空探测任务中的航天员辐射防护设计提供参考。

1 磁场主动屏蔽的理论分析研究

1.1 磁场主动屏蔽原理

高能带电粒子在屏蔽磁场中运动主要受洛伦兹力作用，可忽略非电磁力的影响，描述方程为

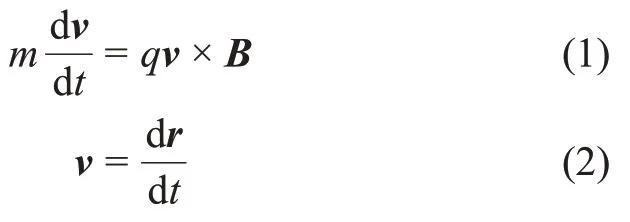
其中：m、q、v和r分别为带电粒子的相对论质量、带电电量、运动速度和位置；B为r处的屏蔽磁场强度。

因宇宙线粒子能量较高，需要考虑相对论效应。在洛伦兹力的作用下，带电粒子在屏蔽磁场中的偏转半径为rL

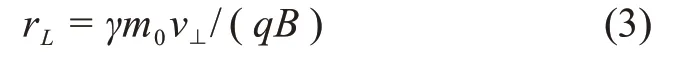
其中：γ为洛伦兹因子；m0为粒子静止质量；v⊥=vsinθ；θ为粒子入射方向v与屏蔽磁场B的夹角。

若屏蔽磁场厚度为L，当L≥2rL时，带电粒子将被完全屏蔽，磁场屏蔽与粒子入射方向无关；当L＜2rL时，只有部分带电粒子被磁场屏蔽，给定GCR/SPE能谱时屏蔽效率取决于屏蔽磁场构型。屏蔽磁场强度和粒子动能一定时，对于原子序数Z ≥2的元素，质荷比大致相等，屏蔽磁场对其偏转能力相近。故本文中，以H和He元素代表典型的GCR/SPE粒子。

1.2 屏蔽磁场的截止动能

截止动能是入射粒子穿过屏蔽磁场到达防护区某指定位置所需的最低动能，与屏蔽磁场构型有关。为了更好地理解截止动能与屏蔽磁场各参数之间关系，采用理想直线型（螺线管）屏蔽磁场结构，如图1所示，由两个嵌套的同心圆柱体组成，小圆柱体为防护区（受保护区），大小圆柱体之间为磁场屏蔽区（偏转粒子），整个结构两端称为端盖区，中间称为桶状区。假定屏蔽区磁场大小均匀，屏蔽区外磁场为零。

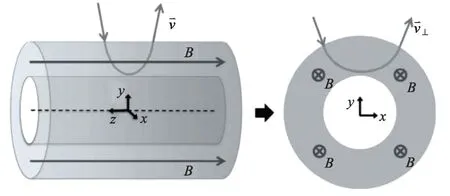
图1 直线型屏蔽磁场构型Fig.1 Linear magnetic field configuration

1.3 无限长构型和有限长构型

对于无限长直线型屏蔽磁场构型，端盖区对带电粒子是全屏蔽的，只需重点关注从桶状区侧面入射的粒子。计算可得到不同屏蔽磁场参数B、L下H和He通过圆心处的截止动能，如表1～2 所示。在磁刚度BL相同的情况下，增大磁场强度B，截止动能更高，即屏蔽效果更好。

表1 H截止动能（GeV/n）Table 1 Cutoff energy of proton

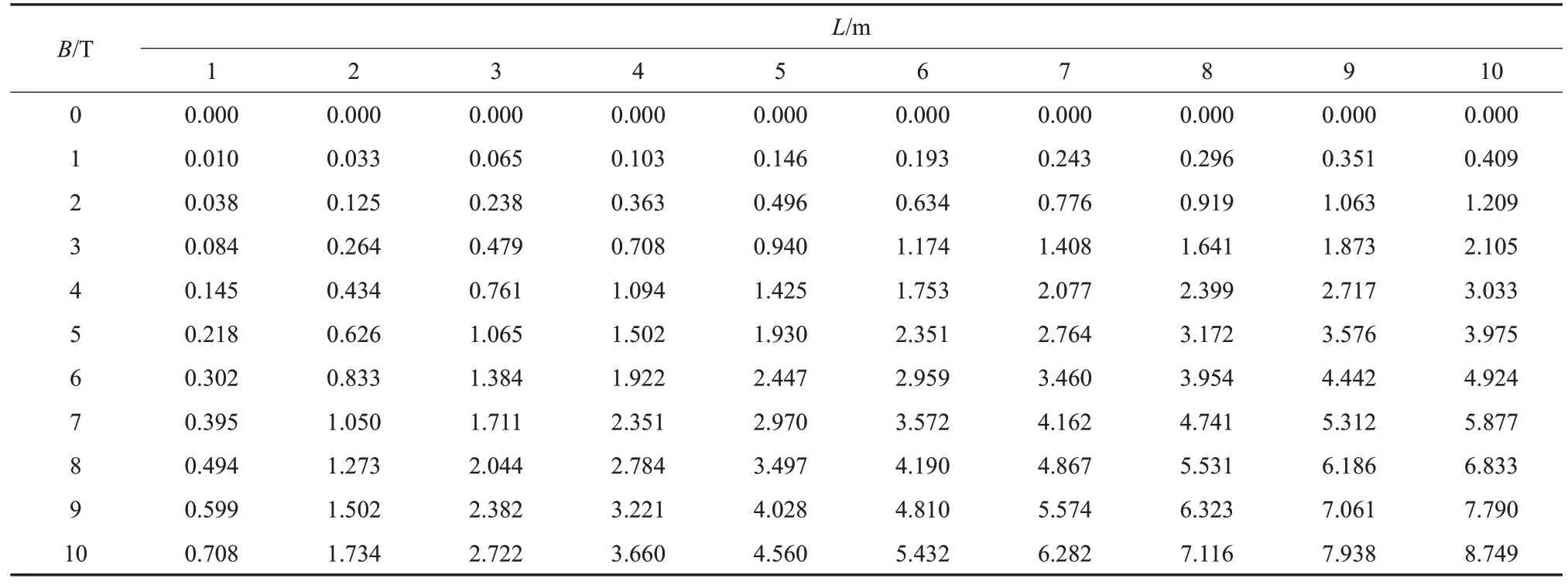
表2 He截止动能（GeV/n）Table 2 Cutoff energy of He

考虑三维情况，取带电粒子与屏蔽磁场轴向夹角（即投掷角）为θ，截止动能随投掷角θ以1/sinθ变化。如图2所示，当θ=90°时，截止动能最小；当θ趋向于0°或180°时，截至动能趋于无穷大。

图2 无限长屏蔽磁场中截止动能随投掷角θ的变化Fig.2 The relationship between cutoff energy and throwing angle in infinite magnetic field

有限长或两端开放式的直线型屏蔽磁场构型更加接近实际情况。有限长直线型屏蔽磁场构型端盖区对截止能量范围内的粒子几乎无防护，尤其是对于有限尺寸的航天器而言，当磁场强度较大时，端盖区是进入防护区辐射粒子的主要来源，因此必须加强端盖区的辐射防护。图3是有限长直线型磁场截止动能随投掷角θ的变化，整体的变化趋势是关于投掷角θ=90°对称的：两端无磁场防护区域，截止动能为0；当投掷角θ逐渐偏离90°时，截止动能先增大后减小到0。

图3 有限长屏蔽磁场中TC/O随投掷角θ的变化Fig.3 The relationship between cutoff energy and throwing angle in finite magnetic field

2 磁场主动屏蔽效率分析研究

2.1 入射粒子源模型

GCR 在空间中呈各向同性分布，假定GCR 粒子呈球面源入射，本文采用蒙特卡洛方法模拟入射粒子源。使用2 个随机数ξ1,2⊂[0,1]来定义球面上的随机位置，若给定辐射粒子初始入射动能或对应的初始入射速度v，即可得到球面上入射粒子的速度分布和随机位置分布，即

其中：μ= cosθ，θ∈ [0,π]，φ∈[0,2π]，三者组成了球坐标{v,φ,θ}。

图4是随机在半径为2 m球面上取5 000个点，试验点均匀分布在球表面，满足各向同性的随机位置分布特征。实际计算中，根据GCR 能谱对不同能量粒子进行抽样，每种粒子统计数量不少于1万个。

2.2 无限长磁场构型的屏蔽效率

为有效评价磁场的屏蔽效果，通过比较无磁场与有磁场状态下进入防护区的带电粒子数来评判磁场的屏蔽效率。对无限长直线型屏蔽磁场构型，只需考虑屏蔽磁场桶状区表面对辐射粒子的防护效果。图5为不同屏蔽磁场强度B、屏蔽磁场厚度L下，无限长直线型屏蔽磁场构型对H（2 GeV）的屏蔽效率。当屏蔽磁场厚度L确定时，通量减少率随屏蔽磁场强度B增大；当屏蔽磁场强度B确定时，通量减少率随屏蔽磁场厚度L增大。总体而言，通量减少率随BL增大，并且均呈现先缓慢增长到快速增大，最后缓慢增长到完全屏蔽的效果。当BL=19 Tm 时，达到全屏蔽。

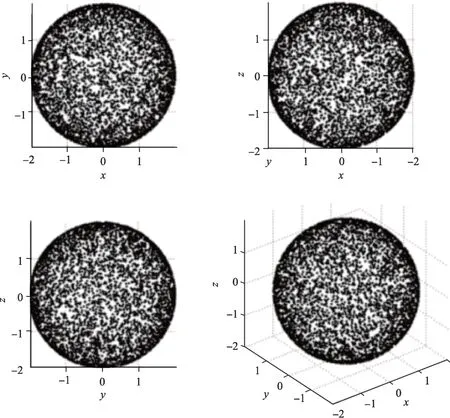
图4 球表面随机取点分布Fig.4 Random distribution of spherical surface

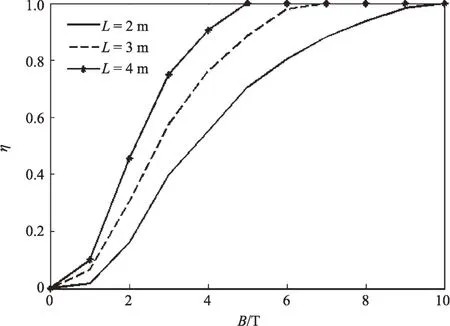
图5 无限长屏蔽磁场对H粒子的屏蔽效率Fig.5 The shielding efficiency of infinite magnetic field to proton

图6考察屏蔽磁场对Z≥2 离子的屏蔽能力。显然，在相同屏蔽磁场构型下，对He 粒子的屏蔽效果显著降低。主要是因为Z≥2 的元素携带一定量的中子，质荷比为H粒子的2倍左右。He粒子在磁场中的偏转半径同样为H粒子的2倍左右，因此屏蔽磁场对其偏转能力较弱。当磁刚度BL=40 mT 时，能够实现对2 GeV/n He粒子全屏蔽。

图6 无限长屏蔽磁场对He粒子的屏蔽效率Fig.6 The shielding efficiency of infinite magnetic field to He

2.3 有限长磁场构型的屏蔽效率

图7为有限长直线型屏蔽磁场构型下H（2 GeV）粒子的屏蔽效果。防护区内径ri=4 m，屏蔽磁场厚度L=2 m，屏蔽磁场轴长z=10 m。由图7可知：当屏蔽磁场厚度L确定时，通量减少率随屏蔽磁场强度B先减小后增大；当屏蔽磁场强度B较大时，通量减少率随屏蔽磁场厚度L增大。当磁场强度B＜2 T时，磁场几乎无屏蔽作用，且出现显著的负作用效果；当磁场强度2 ＜B＜10 T 时，通量减少率随磁场强度B快速增大；当磁场强度B＞10 T时，通量减少率随磁场强度B缓慢增大，最后趋于平缓。当磁场强度B=20 T时，对2 GeV H粒子的屏蔽效率不及0.7。与无限长磁场构型相比，整体屏蔽效果下降明显，且L的变化对屏蔽效果的影响减弱。

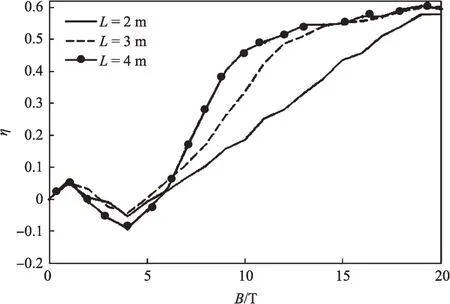
图7 有限长屏蔽磁场对H粒子的屏蔽效率Fig.7 The shielding efficiency of finite magnetic field to proton

图8为有限长直线型屏蔽磁场构型下He（2 GeV/n）粒子的屏蔽效果。与图7相比，整体变化趋势相一致，但屏蔽能力下降。当磁场强度B＜6 T 时，磁场几乎无屏蔽作用，且出现显著负作用效果；当磁场强度6 ＜B＜15 T 时，通量减少率随磁场强度B快速增大；当磁场强度B＞15 T时，通量减少率随磁场强度B缓慢增大，最后趋于平缓。当磁场强度B= 20 T时，对2 GeV/n He粒子的屏蔽效率不及0.6。

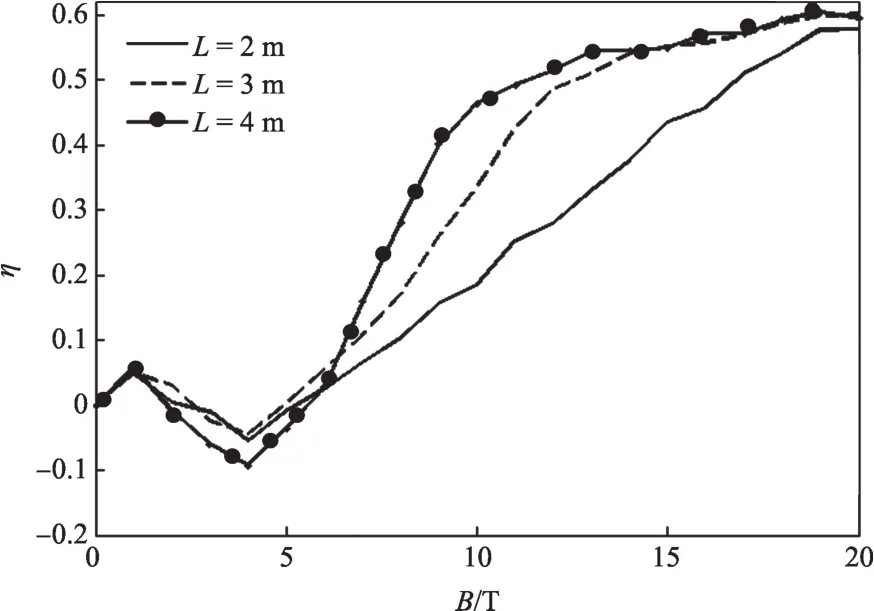
图8 有限长屏蔽磁场对He粒子的屏蔽效率Fig.8 The shielding efficiency of finite magnetic field to He

于无限长屏蔽磁场构型相比，有限长屏蔽磁场构型屏蔽效果显著下降，其原因是端盖区无磁场防护，使得辐射粒子能够无阻碍地进入。此外，屏蔽磁场对部分从两端入射粒子的偏转作用也可能会促使辐射粒子进入防护区，从而降低防护效率，甚至引起负作用效果。因此，在屏蔽磁场构型整体设计时，需要考虑在端盖区增加屏蔽磁场。

2.4 对比验证

针对Spillantini[14]设计的磁场防护结构，计算了对质子能谱的屏蔽效果，结果如图9所示，B= 0，Spillantini - H 代表文献中采用的初始能谱；点线B=0，OMERE - H为计算中采用的初始能谱，其余点线为计算结果。二者屏蔽能谱的变化趋势一致，微弱的差异来自于初始输入能谱的不同。

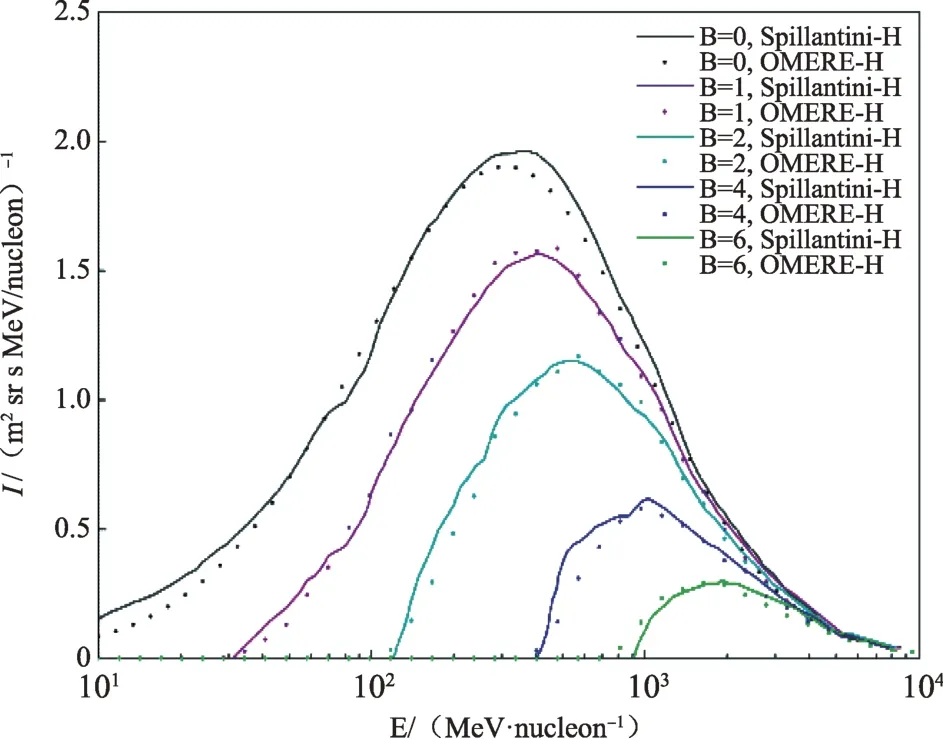
图9 不同磁场强度下的质子屏蔽能谱Fig.9 The proton spectra under different magnetic field

3 磁场主动屏蔽构型设计

3.1 屏蔽磁场结构

对Hoffman屏蔽磁场构型[15]进行改进，研究了环型和直线型2种基本磁场位型，在桶状区和端盖区分别进行组合，进一步考虑端盖区是否覆盖桶状区，共设计了8种理想型屏蔽磁场构型。重点考察端盖区和桶状区磁场构型对屏蔽效率的影响。在此基础上，对实际磁场构型设计进行改进和优化。研究表明，端盖区和桶状区均采用直线型屏蔽磁场构型，屏蔽效率最佳。

3.2 屏蔽磁场基本参数

考虑典型的圆柱体型防护区（航天器）尺寸Φ=7 m×7 m，即半径3.5 m、长度7 m。考虑同心圆柱体型屏蔽磁场，若厚度L= 1.5 m，屏蔽磁场基本参数为：内径ri=3.5 m，外径ro=5 m，轴长l=10 m。本文中屏蔽磁场设定均为理想磁场，即在设定区内磁场分布均匀、设定区外无磁场。仍以H 和He 元素代表典型的GCR粒子。

3.3 不同磁场构型的屏蔽效果对比

对比分析了表3所示的屏蔽磁场构型在不同磁场强度B和厚度L下对能量为2 GeV/n 的H 粒子的屏蔽效果，如图10～11所示，图10中屏蔽磁场厚度L=1.5 m，图11中磁场强度B=3 T。

表3 屏蔽磁场构型Table 3 Shielding magnetic field configuration

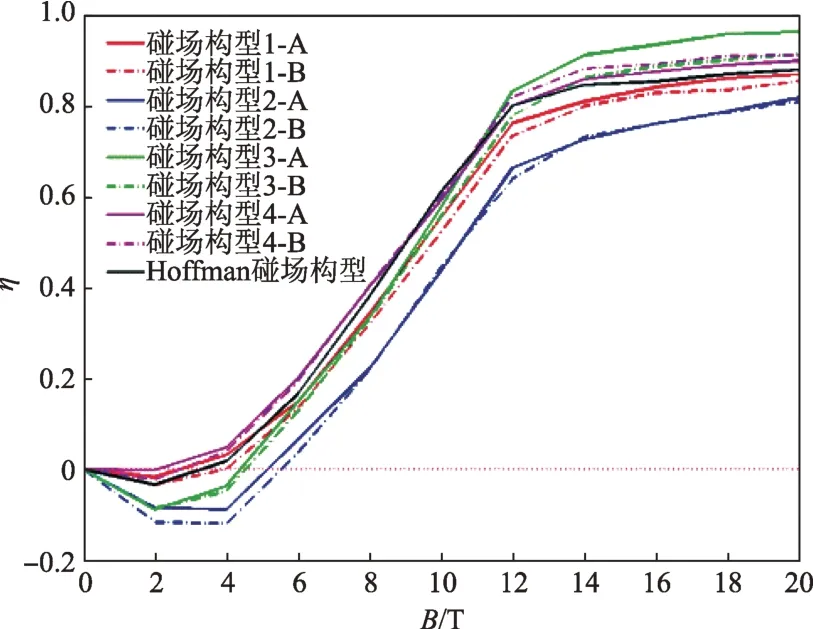
图10 不同磁场构型对H（2 GeV）屏蔽效率Fig.10 The shielding efficiency to proton of different magnetic field configuration

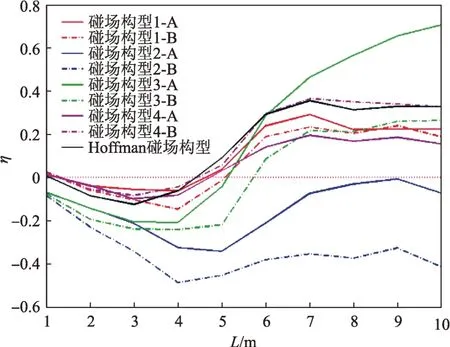
图11 不同磁场构型对He（2 GeV）屏蔽效率Fig.11 The shielding efficiency to He of different magnetic field configuration

对比图10和图11，当磁刚度BL一定时，增大磁场强度B获得的屏蔽效果要优于增大磁场厚度L。因为，磁场对带电粒子的作用效果有3种：①能阻止在无屏蔽磁场时进入防护区的那些带电粒子，通量减少率增加，称为促进效果；②不能阻止在无屏蔽磁场时进入防护区的那些带电粒子，通量减少率不变，称之为无用效果；③偏转无屏蔽磁场时不能进入防护区的那些带电粒子使其进入防护区，导致通量减少率出现负值、屏蔽效果变差，则称之为反作用效果。增大磁场强度B，磁场的促进效果增强，同时无用效果与反作用效果会显著降低；L增大，理论上磁场的屏蔽能力增强，然而由于L增大导致反作用区域的面积占比增大，使得磁场的反作用效果增强，则屏蔽能力出现起伏。对比表3所列的9种磁场构型，A组构型明显优于B组构型，磁场构型3-A的屏蔽效果最好。

3.4 最优磁场构型对GCR能谱的屏蔽效果

计算中辐射源采用典型银河宇宙线极大下的H和He 微分能谱，其中H 占90.18%，He 占8.94%。图12～13给出了磁场构型3-A 下H 和He 能谱随屏蔽磁场强度B的变化。

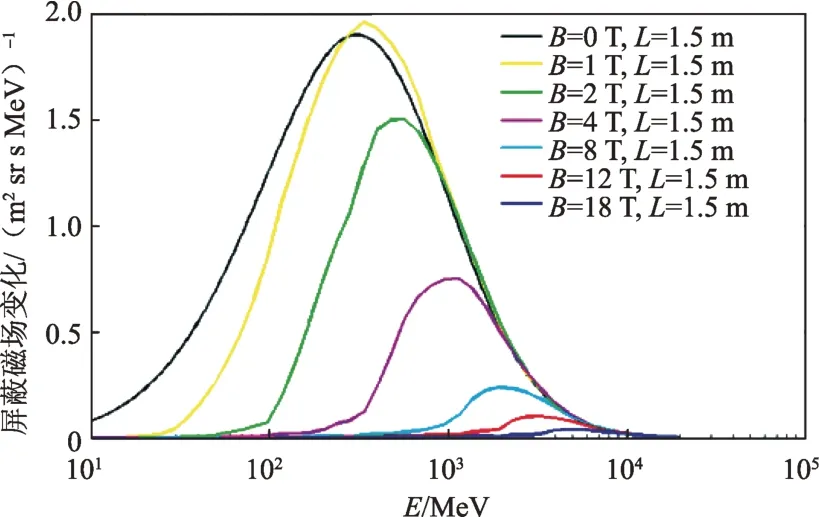
图12 磁场构型3-A对H能谱屏蔽效果Fig.12 The shielding efficiency to proton of magnetic field

从图13可以看到，在L=1.5 m、B=18 T时，磁场构型3-A的屏蔽方案对H通量减少96%，He通量减少85%，总通量减少约90%。

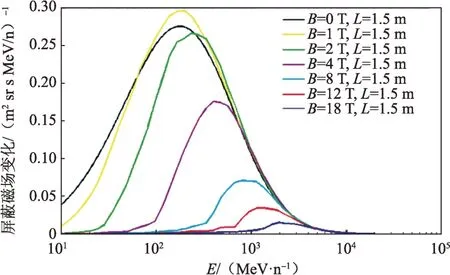
图13 磁场构型3-A对He能谱屏蔽效果Fig.13 The shielding efficiency to He of magnetic field

4 结 论

本文基于单粒子轨道理论和蒙特卡洛方法建立了一种磁场主动屏蔽防护分析方法，针对理想磁场构型，考察了屏蔽磁场结构、强度和厚度对屏蔽效果的影响，主要结论如下：

1）屏蔽效率随磁刚度BL增大，当BL一定时，增加磁场强度B有利于提升屏蔽效率。

2）有限长屏蔽磁场构型，端盖区需加强防护，特别是端盖区占总表面积过大的情形，是辐射粒子进入防护区的主要来源。

3）端盖区和桶状区磁场位形、磁场厚度和磁场强度是影响屏蔽效率的主要参数。整体上，桶状区与端盖区采用直线型屏蔽磁场的3-A构型，防护效果最好。

致谢

感谢南京航空航天大学黄朝艳老师在分析计算中给予的帮助。