基于神经滑模变自抗扰控制的感应电机变频调速系统的研究与设计＊

郭金妹，张建荣，陈 磊

（江西应用技术职业学院 机械与电子学院，江西 赣州 341000）

1 引言

近年来，交流调速系统发展十分迅速，而感应电机因其运行可靠、成本低廉、高效节能等优点，在变频调速系统中占有重要的地位。但是感应电机本身是一个多变量、强耦合、非线性的时变系统，其电磁转矩、速度、数学模型构建都很难精准控制，使电机的调速性能无法有效提高。目前典型的感应电机变频调速现代控制理论有四种：转速开环恒压频比（V/F）控制、转差频率控制、矢量控制（FOC）和直接转矩控制（DTC）。其中前两种控制理论只对电机的标量进行控制，依赖于感应电机的稳定模型；后两种控制理论是对电机的矢量进行控制，依附于感应电机的动态模型，虽然实现对电机的实时控制，但坐标变换复杂，无法有效提高调速性能且造价高。

将现代控制理论与非线性控制理论相结合，应用于感应电机变频调速系统，打开了感应电机的高性能调速研究的新局面。其中，亢振勇等专家提出利用传统PID控制融入矢量控制中实现电机磁链和转矩的完全解耦，但PID仅考虑外部因素，对自身带有更多内外部不确定性因素的感应电机无法准确控制。随后，韩京清教授利用特殊非线性结构充分挖掘误差信息，提出自抗扰控制技术（ADRC），实现了电磁转矩和速度的复合控制。但其参数极多，整定控制要求较高，从而限制了ADRC的应用。为了减少自扰抗控制器的整定参数，一些学者将滑模变结构（SMC）与自抗扰控制相结合，不但减少了参数整定数量，而且使系统的误差尽可能地沿着滑模面趋于平衡点，有效提高调速系统的精度。因此，本文立足于当前研究，提出了基于神经滑模变自抗扰控制的感应电机变频调速系统。ADRC控制器与SMC控制的有效结合，构造滑模变自抗扰控制器，并将神经网络智能控制融入滑模变自抗扰控制器，可降低控制器对系统精准数学模型的依赖，减少调速系统的自扰动，有效提高调速品质和响应速度。

2 感应电机变频调速系统的数学建模

感应电机是一个非线性时变控制对象，在实际工况中，电机电阻、电感、气隙磁通会受到环境的干扰影响。因此，为了分析方便，通常需要忽略谐波的影响，做出理想的假设。根据查阅相关资料和数学逻辑推导，得出感应电机矢量控制下的数学模型表达式：

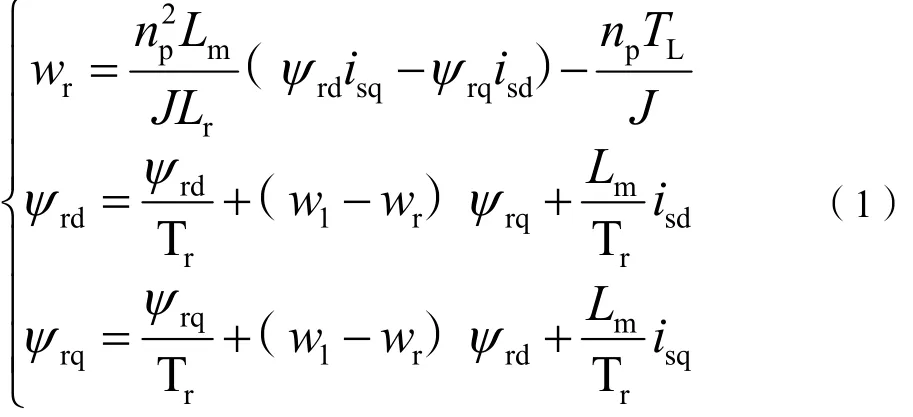
式（1）中：ψrd，ψrq为转子磁链；isq，isd为定子电流；TL为转矩；J为转动惯量；Tr为常数。

在计算化简过程中，对感应电机变频调速系统数学模型采用Clarke变换和Park变换，通过变换后，系统数学模型得以简化，极大减少了变量之间的耦合程度和状态变量的数量。根据式（1），可绘制出其对应的结构框图，如图1所示。图1在传统矢量控制的基础上，增加了位置控制器、SVPWM和逆变器环节，形成了位置-速度-电流三环控制的变频调速控制系统。控制系统使电流传感器采样三相电流经过坐标变换成d-q轴下的电流，反馈到电流控制器，分别控制电机的励磁和电磁转矩。电流环作为系统的最内环，其带宽大小决定了整个系统的响应性能，位置检测通过编码器等传感器检出，对位置信号进行微分，可得到电机的转速信息。

图1 感应电机变频调速系统结构框图

3 神经滑模变自抗扰控制器的设计

3.1 滑模变自抗扰控制器的构造

随着控制技术的快速发展，经典的PID已不能满足系统控制精度和速度的要求，因此，中科院韩京清教授提出了自抗扰控制技术（ADRC）来弥补PID的不足。ADRC控制器由跟踪微分器、非线性反馈律、扩张状态观测器和自抗扰控制器组成，其中跟踪微分器用来处理给定信号的微分；针对线性反馈律速度和精度不足等问题建立非线性反馈率；通过建立扩张状态观测器抑制扰动，减少误差；自抗扰控制器实时补偿误差，消除系统的不确定和扰动部分。

从感应电机变频调速系统的数学模型可以明显看出，转子磁链在进行坐标变换时，d轴上的磁链和电流均存在耦合，在应用非线性控制理论对数学模型进行解耦处理过程中，难免给系统带来不必要的误差，从而影响控制精度。因此，利用ADRC可有效解决这一问题。在ADRC设计过程中，采用三个一阶ADRC控制器分别对调速系统的转速、电流和位置实现控制，三个一阶ADRC设计参数不同，位置检测对位置进行控制，速度检测对转子角速度进行观测，电流检测对电路电流进行调节。通过分析发现，ADRC兼顾了对象的外部不确定因素和感应电机的内部状态，实现高宽带响应的转速环和电流环控制，但其控制参数依旧较多，整定过程困难。因此，为了减少自抗扰控制器的整定参数，提高调速系统的鲁棒性，引入滑模变结构（SMC），构造滑模变自抗扰控制器。通过计算得出滑模速度调节器输出式：

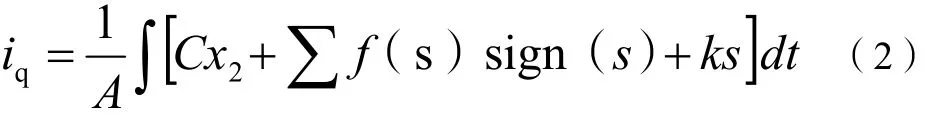
选用速度误差作为滑模变结构控制器的状态变量，在控制律的作用下输出结果为矢量变换q轴电流的输入量，同时在积分器的作用下，有利于消除稳态误差，有效提高系统的稳定性。通过对自抗扰控制技术和滑模变结构控制技术的分析，得出感应电机变频调速系统滑模变自抗扰控制器，其系统结构如图2所示。

图2 变频调速系统自抗扰控制系统结构图

3.2 神经滑模变自抗扰控制器的构造及作用

神经网络逆系统的构造是将其进行线性化、解耦成伪线性系统的重要前提。逆系统实现方法有解析实现和非解析实现两种，其中非解析实现在逆系统表达式未知情况下也能实现系统构造。感应电机是一个多输入多输出、强耦合非线性的高阶系统，其精确数学模型难以用精确解析式表示出来，只能用近似模型代替，而由于神经网络能以任意精度逼近复杂的静态非线性函数，因此运用神经网络来实现被控系统的逆系统，从而构造出非解析实现形式的逆系统。

滑膜变自抗扰控制器不仅提高了感应电机变频调速系统的响应速度和精确度，而且有效减少了参数整定数量，提高系统的鲁棒性。然而，这一控制器仍需建立在被控对象精确的数学模型之上，而感应电机调速系统本身是一个多变量的时变系统，建立精确的数学模型较为困难。因此，本系统引入神经网络逆控制，应用BP学习算法不断逼近调速系统数学模型和滑模变自抗扰控制器控制函数，运用经归一化处理的数据来训练和校验神经网络，选取2/3变换数据为训练数据集。在对数据进行离线训练过程中，不断采集不同转速、磁链给定下转速、磁链、电压、电流等实验数据，直至训练误差达到要求。神经滑模变自抗扰控制器结构如图3所示。

4 仿真及结果分析

利用Matlab中的simulink环境下搭建起感应电机变频调速系统神经滑模变自抗扰控制器仿真模型，其中感应电机和SVPWM模型采用S函数建模；位置控制器（APR）、速度调节器（ASR）采用PID调控；电流调节环（ACR）采用PI调节；滑模变控制（SMC）、自抗扰控制（ADRC）和神经网络逆控制（CNN）均用模块化表示，仿真整体模型如图4所示。

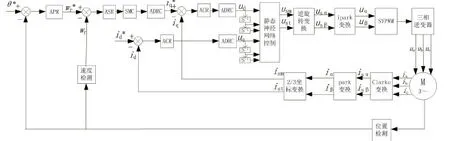
图3 感应电机变频调速系统神经滑模变自抗扰控制器结构图

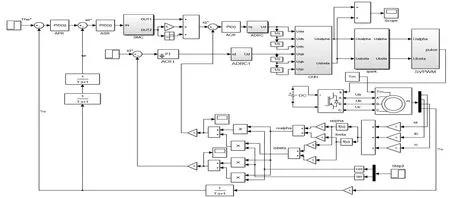
图4 感应电机变频调速系统神经滑模变自抗扰控制器仿真模型

仿真过程中感应电机参数如表1所示，通过不断调节仿真模型参数，并将神经滑模变自抗扰控制调速系统与仅加入PID算法的变频调速系统进行比较，响应对比结果如图5所示。仿真结果表明，加入神经滑模变自抗扰控制算法的变频调速系统比只加入传统PID控制的变频调速系统具有更好的调速品质，且控制平稳有效，响应速度更快。

5 结束语

在掌握感应电机特征的基础上，研究感应电机变频调速系统的状态表达式，后基于该数学模型将自抗扰控制器和滑模变控制器结合构成复合控制器，引入神经网络逆控制，并构造神经滑模变自抗扰控制器的状态方程和结构框图，最后在Simulink环境进行仿真验证。

从仿真结果可得出，基于神经滑模变自抗扰控制的感应电机变频调速系统具有调速平稳可靠、响应速度快、抗干扰能力强等特点。

表1 感应电机主要参数

图5 感应电机变频调速系统响应对比曲线