基于模糊理论的城市道路立交设计及综合评价分析

邓称意

（深圳市市政设计研究院有限公司，广东 深圳 518000）

0 引言

随着我国经济的快速发展，大中型城市的机动车拥有量也在不断提高，平面交叉口成为城市道路中的瓶颈。立体交叉利用跨线构造物使道路与道路在不同的空间相互交叉，可以有效地解决道路交叉口的交通冲突，以实现道路之间空间交叉和行车方向的快捷转换[1]。

城市道路路网密集，交通转换需求大，受用地条件影响，城市立交的使用更为频繁和复杂。特别对城市道路规划落后于城市发展的地区或者片区而言，受先天规划不足的影响，立交方案的选择既要符合现状，且能满足近远期道路交通功能及城市发展需求，因此对立交的综合设计和评价提出了更高的要求。

因城市立交方案影响因素复杂，指标繁多，对于每座立交，由于地理位置，使用功能，社会条件、环境条件、自然条件的差异，影响因素及其影响程度也不尽相同，具体的评价指标也不一样。目前国内城市立交方案设计评价沿用公路立交的技术经济比较法，该方法简便直观，操作性强，但未进行指标的综合量化，带有很大的经验性和局限性。因此，本文通过充分分析城市立交设计特点及评价指标体系，采用定量与定性相结合，探讨基于模糊理论的立交综合评价方法。

1 城市立交分类及设计特点

1.1 城市立交分类

城市立交的种类繁多，类型多样，各类互通式立交均有各自的特点和适用条件，根据不同的分类方式可将其划分为不同类型[2-3]：

（1）按相交道路数可分为两路立交、三路立交、四路立交和多路立交；

（2）按相交道路是否互通可分为分离式立交，完全互通立交或部分互通立交；

（3）按立交主线及匝道的空间层次可分为两层式立交、三层式立交或四层式立交等；

（4）按立交匝道的形式可分为定向式立交、半定向式立交及非定向式立交；

（5）按相交道路的等级可分为枢纽立交或一般立交；

（6）按立交类型可分为组合式立交或非组合式立交；

（7）按立交的外形可分为喇叭形、苜蓿叶型、叶型、梨型、环形、蝶形及菱形等；

（8）按匝道的布设位置可分为一象限式、两象限式（对角线式和相邻象限式）、三象限式、四象限式；

（9）按立交匝道交通功能可分为迂回式和直达式等。

1.2 城市立交设计特点

城市立交因规划控制、路网密度、用地条件、经济水平、环境影响等因素影响，与公路立交相比，具有明显的城市特征。

1.2.1 立交规划特点

城市立交规划布局可分为两种：（1）城市总体规划完善，路网规划科学合理，立交布局符合城市交通远期发展。该类立交设计往往控制因素较少，立交设计预留条件较好。（2）城市总体及交通规划落后，属被动型立交设计，往往为了解决现状及近期交通压力增设立交，控制因素多，立交设计难度大。

1.2.2 交通功能特点

城市立交除需考虑车行交通功能外，同时需充分考虑慢行的交通需求。特别是当前对慢行交通需求及舒适性要求越来越高，立交设计前期构思需同时考虑车行及慢行的总体布局。

1.2.3 立交组合特点

除城市内高速公路外，城市立交大多无收费站，且因车速相对高速较低，对主线和匝道的平纵线型较为宽松，可供选择的立交形式和组合方式多，往往立交设计更复杂多样，赋予设计者更多的发挥空间。

1.2.4 环境特点

城市立交一般环境条件比较复杂，除现状地形条件外，往往受征地拆迁、现状管线、现状轨道等因素影响。因此设计时，需充分调研现有地面、地下建构筑物情况，通过多方案比选，合理确定主线及匝道的平面及竖向关系，推选最佳方案。

1.2.5 城市景观特点

城市立交多处于交通转换集中点，大量车流及人流需通过立交进行交通转换，良好的立交设计会给驾驶人、行人心情愉悦，因此对立交的景观提出了更高的要求。在立交设计时，应充分考虑利用好现状条件，在解决交通功能的同时，让城市立交成为城市的景观窗口。

2 城市立交方案设计的指标体系及评价模型

立交方案设计是指在立交设计前进行的立交总体安排布局工作，旨在进行立交类型选择及比较，确定合理、适用、经济、美观的立交方案。立交方案比选一般分为四步：（1）经过初步分析，筛选，提出明显不可行方案，确定2～5个可比选方案；（2）建立方案比价指标体系；（3）指标评价；（4）方案比选结论及推荐。

2.1 城市立交综合评价体系的建立

目前立交评价的指标体系多数是按层次来划分。指标分层是将各指标性质，影响特性和影响效果进行归类，并按隶属关系进行分层。第一层为目标层，表征方案的最终评价结果，用于不同方案间的比选；第二层为准则层，是综合评价的中间层，表征方案在某一方面特征的大类指标，如方案的运行情况，实用情况、费用情况等是同一类分项指标的集合，这是方案比较的基本层次；第三层为指标层，是描述方案细部特征的指标，如用地面积，回收期，景观协调等，这是方案的基础层；第四层为子指标层，根据需要设计各子指标[4]。

影响立交方案的各方面因素复杂，指标繁多。对于每个立交所处地理位置，使用功能、社会条件、环境条件、自然条件的差异，影响因素及其影响的程度也不相同，具体的指标也不尽相同。现根据城市立交特点，初拟了城市立交指标（包含但不限于）体系如表1所列。

表1 城市立交指标一览表

2.2 基于模糊理论的立交方案综合评价模型

模糊数学理论最早是在1965年由美国的计算机与控制论专家扎德提出，它是一种研究模糊性或不确定性问题的理论方法。模糊数学的核心思想就是通过用数学的手段来仿效人脑的思维，建立对复杂事物进行模糊度量、模糊识别、模糊推理、模糊控制和模糊决策的本领[5，6]。

2.2.1 立交方案模糊评价模型

通过拟定m个立交方案组成方案集V=｛v1，v2，…，vm｝，其中vj为第j个立交方案。评价立交方案的评价因素或指标共有n个，其中定量因素为n1个，定性因素n2个（n1+n2=n），计定量因素集为U1、定性因素集为U2，由所有影响因素组成的因素集为U=U1∪U2=（u1，u2，…un，un+1，…，un），其中ui为第i个影响因素（或评判因素，简称因素）。进行立交方案单因素评判时，第i影响因素的单因素评判集Ri=｛ri1，ri2，…，rm｝，综合立交方案全体单因素评判结果，即可得到立交方案优劣的单因素评判矩阵，如式（1）所示：

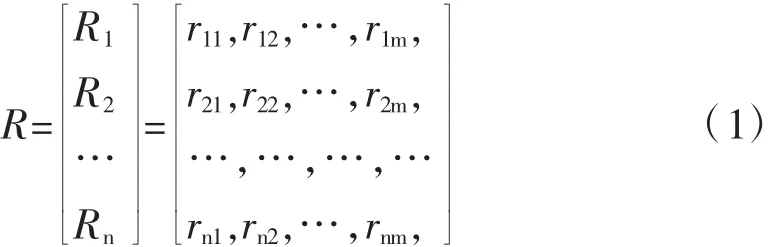
其中，rij为第i个因素ui对j立交方案vj的隶属度。

进行立交方案影响因素权重赋值时，应充分考虑各因素对立交方案的重要性程度，同时结合考虑立交方案交通功能、技术指标、经济性、环境指标、管理指标等因素，对各因素赋予不同的权重，得到立交方案评价各影响因素的权重集A=｛a1，a2，…，ai…，an｝，其中ai为第i因素ui的权重，ai≥0，综合以上分析，得到模糊综合评判结果即得评判集如式（2）所示：

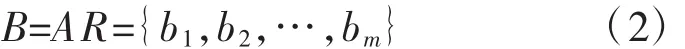
式中，bi为综合考虑所有因素的影响时，评判对象对第j个方案类型vj的隶属度，即评判指标rij，通过比较评判指标bi值的大小，对不同立交方案的优劣进行排序，bi值越大，表示第j个立交方案综合性能越好。

2.2.2 模糊关系的量化

在进行立交方案综合性能评价之前，必须对立交方案的因素值进行量化，确定单因素模糊评判矩阵R，即确定隶属度。根据影响因素的性质，从定量因素和定性因素两个方面来分析。

（1）定量因素的隶属度。考虑定量因素的各指标值之间的量纲不同，且指标值变化范围差异也较大，现按照最优值相对隶属度为1的原则，定义隶属度。

对于值越大越优型因素（所谓越大越型因素是指因素指标值以最大值为最优，反之则为越小越优型因素）的隶属度按式（3）、式（4）进行计算：

对于越小越优型因素，其隶属度为：

式中，rij为第j个立交方案中项因素的指标值；max｛yij｝与 min｛yij｝分别为各类方案中i项因素指标的最大值和最小值。

（2）定性因素的隶属度。定性因素以模糊语言来表示，例如优、良、中、差等，并以此来表示不同立交方案相对比较而言的性能。以有利于立交为优，最不利者为劣，一般可以分为5级，即优、良、中、次、差，相对应的隶属度分为 1、0.75、0.5、0.25、0。对于处于等级中间过渡的状态者可以用线性内插的办法，确定其相应的隶属度。若参加定性因素评级的专业人员对评级意见不一致，可以按百分比计入。

3 基于模糊理论的某城市互通立交设计及综合评价案例分析

3.1 立交节点分析及方案设计

3.1.1 立交节点概况及交通量预测

该立交节点位于广东省深圳市，相交道路等级均为城市Ⅰ级主干路，双向6车道，设计车速50 km/h，匝道设计车速30 km/h。根据城市道路交叉口设计规范，结合节点交通量预测，该立交节点为全互通立交，具体交通量预测如图1所示。

图1 远期交通量预测结果示意图

3.1.2 立交节点控制因素

该节点位于建成区，节点涉及现状拆迁较大，南侧为山体，东北侧临时停车场，西北侧为城市更新规划用地；南侧现状高铁距离立交节点中心约400m，且现状跨铁桥已建。因此该立交方案设计主要考虑现状高铁跨线桥、对山体破坏、房屋拆迁及道路城市用地的影响。

3.1.3 节点方案设计

该项目方案根据规划用地，结合道路现状条件，在满足远期交通功能情况下拟定了三个可行性方案（考虑东北侧地块整体性，方案均考虑用地预留，即尽可能预留第二象限用地条件），主线最大纵断坡4%、匝道最大纵断坡5%控制，具体方案如图2、图3、图4所示。

图2 方案一：对角象限苜蓿叶+半定向匝道互通立交示意图

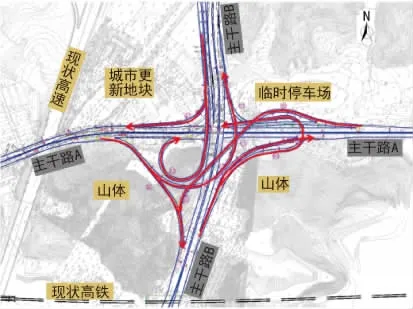
图3 方案二：环形+掉头+半定向匝道组合式互通立交示意图

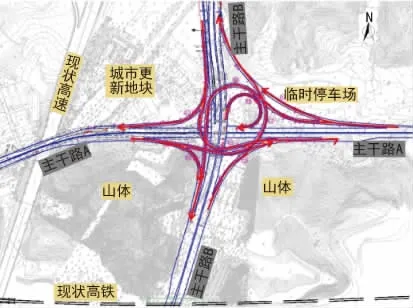
图4 方案三：集约形组合式立交示意图

方案一：采用常规对角象限苜蓿叶立交形式，通过两个环形匝道及两个半定向匝道实现道路左转向交通功能，交通指示清晰。

方案二：结合远期交通量预测，充分利用道路高差关系及地形条件采用环形+掉头+半定向匝道实现左转交通功能，交通指示相对清晰，掉头匝道（远期预测交通量为309 p c u/h），绕行较远。

方案三：充分利用东北侧第一象限集中布置立交匝道，减少山体开挖及立交总体占地，因集中单象限展线，部分匝道相互跨越，立交匝道平纵线形指标相对较低。

3.2 立交方案综合评价

3.2.1 立交方案评价指标分析及权重赋值

根据2.1节中城市立交评价指标表，结合该立交方案特点，忽略如交通疏解、管线迁改、饱和度、分期修建适应性等与此次节点方案评价关系较小（或无关）的指标，选取对此次方案优选有针对性评价指标，具体指标评价量化及评价指标赋值如表2所列。

表2 立交方案评价指标一览表

3.2.2 立交方案各因素的隶属度计算

根据3.1节点评价分析结果，结合2.2节中隶属度计算方法，得出各方案不同因素率速度集合如式（5）所示：

3.2.3 立交方案综合评价计算及分析

对三种立交方案的综合评价及计算：

由计算结果分析可知：方案二（环形+掉头+半定向组合互通立交）具有较好的综合性能。从定性角度来分析，方案二虽存在小交通量需求掉头匝道，但总体交通指标与方案一相当，略差于方案三，此外方案二在用地、工程经济、拆迁上具有较明显的优势，因此推荐选用方案二是合适的。从以上分析可知，采用基于模糊理论的立交综合评价方法推选的立交方案具有一定的适用性。

4 结 语

本文通过对城市立交的分类和特点进行基础分析研究，建立了基于模糊理论的城市立交综合评价模型，建立了符合城市立交特点的综合评价指标体系，并结合工程实际案例分析，采用了基于模糊理论的综合评价模型进行方案优选。通过与传统经济技术分析法对比研究，认为基于模糊理论的量化分析方法具有可操作性和适应性。