剪切来流作用下弹性管绕流数值分析

杨福昌， 鲁 丽

(西南交通大学力学与工程学院， 四川成都 610031)

[通信作者]鲁丽(1978～)，女，博士，副教授，主要从事流固耦合振动研究。

随着海洋油气装备技术的迅速发展,深水资源越来越多地被勘测和开发出来。深海资源的开发需要由钻井平台系统、水下生产系统与输油系统组成一套庞大的工业生产体系，在这个体系中圆管处处可见，如海洋勘探平台柱脚、海底管线、立管等。实际工程应用中，如低流速海流发电系统，弹性管通过在剪切流作用下的振动完成水下能源与电能的转换，使海底设备能够得到足够的能源补充以达到持续供电运转；又如在深海的探索中，剪切流传感器被用以测量剪切方向脉动，从而对海洋底部进行测量和研究，这种方法是了解深海内部规律的重要途径[1]，因此准确掌握剪切流作用下圆管的振动特性很有工程应用意义。

目前对于小细长比圆柱体绕流问题研究比较多,Mysa[2]、Wang[3]、Chatterjee[4]近年来对均匀流作用下串连双管做了详细研究。而实际真实的海洋环境中，海水流速并不是均匀分布的，而是流速随着海水深度的变化呈现剪切分布特性。为了更切合实际地研究真实海洋的弹性管的涡激振动响应特性，需要对剪切流场中的细长弹性管的涡激振动响应特性加以研究。由于横向剪切流实验较难实现，目前对于横向剪切流作用下海洋立管运动的实验研究较少。Kang[5]、Sumner 和Akosile[6]等人基于实验方法研究了不同雷诺数时,静止状态下的圆柱体在不同剪切率条件下泻涡频率变化、升力系数和阻力系数的变化。近年随着商业计算软件的快速发展，数值仿真技术应用越来越广，Zhao[7]等人基于(SST)湍流模型研究了高雷诺数下单自由度圆柱体涡激振动问题，准确分析了折减速度对振动幅度与尾流场特性的影响。涂佳黄[8]等人对低雷诺数下二维线性剪切来流作用下弹性支撑圆柱体双自由度流致振动问题进行了数值分析，主要研究了随剪切率变化时，结构共振区间的变化范围以及剪切率和管的振动特性之间的关系。王凯鹏[9]对静止状态串列双圆柱体二维模型在均匀流和剪切率作用下的流场特性进行了比较。

以往对于剪切流作用的单管研究，大多把三维单管简化为二维，主要是探究流场的变化，对结构的变化关注很少。二维简化虽然可以降低模型实验和数值模拟的难度，但当考虑管束的弹性变形时，流场与结构的相互作用变得更复杂，二维仿真无法描述管振动的真实状态。随着计算流体力学(CFD)理论以算机技术的日益发展，三维仿真变得可以实现。本文通过三维数值仿真技术，基于真实海洋环境海底流速遵循从上到下随深度增加逐渐减小的规律[10]，结合材料模型的特征长度，最终选取了雷诺数为150进行数值试验，通过控制流场中心线的速度和特征长度来确定雷诺数。进行横向剪切流的计算时, 必须保证不能发生碰壁现象并且不同剪切率条件下，入口处来流速度必须为正值,以便不会形成回流，因此，选择流场区域为[-15D,45D]×[-15D,15D]，剪切率变化区间为0.01～0.1，增量为0.01。研究了剪切流作用下两端固支的弹性单管的横向振幅、运动轨迹、振动频率和升力系数，探究了低雷诺数下剪切率对弹性单管振动特性的影响。

1 数值模型

运用ANSYS的Workbench的双向流固耦合模块，通过流固耦合交界面进行流体域和固体域间的数据传递，建立流体-结构交互模型。

结构方面选择Transient Stuctural模块，先定义材料属性，在单管上均匀取9个监测点，然后划分网格，设置弹性管两端固支，设置弹性管外表面为双向流固耦合面，最后在结构求解器中选择记录监测点在横向和纵向的位移随时间变化的情况；流体方面选择Fluid Flow(Fluent)块，导入已经在ICEM CFD模块中画好的流场结构化网格，设置入口为速度入口、出口为压力出口、固定端对称边界、上下边界、流场与管接触面为壁面设为双向流固耦合面，流场模型选择为Laminar层流模型，入口流速采用udf编写，主要监测流场的升阻力系数变化；选择System Coupling为数据交互的耦合模块；所有计算模块均设置时间步长为0.1 s，总时间t为60 s。

1.1 区域和计算参数

横向剪切流如图1所示，uc为流场中间速度，k为剪切率，y为横向位移。

u=uc+ky

(1)

k=du/dy

(2)

图1 圆管位于横向剪切流示意

流场区域 [-15D,45D]×[-15D,15D]，流场的网格如图2所示，对漩涡生成、运动的区域以及流场与弹性管接触的流固耦合面进行网格加密。

图2 流场网格整体和局部示意

单管上从B到C均匀分布9个监测点如图3所示，分别为n1到n9通过9个点的变化判断管运动状态的变化。

图3 单管监测点示意

1.2 物理参数

本文使用的材料模型参数[11]：外径0.01 m，内径0.009 5 m，管长0.5 m，弹性模量为10 GPa，泊松比为0.3，管子的密度6 500 kg/m3；流体密度为998.2 kg/m3，比热容为4 812 j/(kg·℃)，导热系数为0.6，动态粘度0.001 003 Pa·s 。

2 双向流固耦合方法

2.1 双向流固耦合基本方法

双向流固耦合基本方法是流场在运动时接触固体，并影响固体结构的形变，固体形变后反作用于流场，使流场运动状态发生改变，两者不断相互作用。

本文采用双向流固耦合中的弱耦合方法，不考虑结构的惯性力，把固体和流体分开，流体域受到的载荷折算为结构的变形，求解时，分别对结构动力方程和流体力方程求解，将前一个物理场的计算结果作为已知条件加载到下一个物理场，从而实现两个物理场的耦合。

2.2 流体力及边界条件

雷诺数的定义：

(3)

式中:uc和D为流场中心线(y=0)处的特征速度和特征长度[12-13]；t为时间；ν为流体运动粘度系数。

外部流体在管道上的作用力包括了升力，附加阻尼及附加质量[14]。公式可表示为：

(4)

Ca=rωSρ0D2

(5)

(6)

式(4)～式(6)中：CL为升力系数，ρ0为管外流体密度，Cm为附加质量系数，取Cm=1.0[15]。ωs为涡激频率，其公式为：

(7)

式(5)中r值公式为：

(8)

CD为阻力系数，St为Strouhal数。

因此，横向流作用下的流体力可以写成：

(9)

常见的边界条件分为非线性约束和线性约束两类，一般支承的边界条件为[16]：

ELw′′′(0)=-K1w(0)

ELw″(0)=-KT1w′(0)

(10)

ELw′′′(L)=-K2w(L)

ELw″(L)=-KT2w′(L)

(11)

K1，K2分别为左右两侧线性弹簧刚度，KT1，KT2分别为左右两侧扭转弹簧刚度。

当两端固支时，K1→，KT1→，K2→，KT2→。此时边界条件可简化为：

w(0)=w′(0)=w(L)=w′(L)=0

(12)

对于非线性约束，只需要在运动方程中添加非线性约束力来分析：

FB=(K3w+K4w3)δ(x-xb)

(13)

式(13)中：K3为线性弹簧刚度；K4为非线性弹簧刚度；为非线性约束轴向位置。

3 数值实验结果和讨论

图4给出了在不同剪切率条件下，计算达到稳定后升力系数时历曲线，由图可知,不同剪切率对升力系数大小的影响很大，升力系数并不以CL=0为中心周期性变化；并且随着剪切率的增大，管升力系数振幅呈不断增大的趋势。由于升力系数曲线均值在零附近不容易观察，为方便观察升力系数的变化规律，图5给出了管升力系数均方根随剪切率变化折线图，由图可见升力系数均方根随剪切率的增大而逐渐增大。

图4 升力系数随时间变化曲线

图5 升力系数均方根随剪切率变化曲线

为了对升力系数的变化规律进一步分析，对升力系数进行傅里叶变化，图6为剪切率0.01～0.1的升力系数频率变化图，由图可以看出剪切率较小时，升力系数频率逐渐上升，在[0.04，0.07]区间内的振动频率为0.25 Hz，离开这个区间后，频率快速下降又逐渐增加。发现在剪切流作用下的绕流运动存在 “剪切率锁定”现象，在这个区间内结构的振动频率不变，结构的升力系数和结构的振幅逐渐增大。

图6 升力系数频率随剪切率变化曲线

为了更好地探究单管振动受剪切率的影响，图7给出了雷诺数为150时，不同剪切率下单管上监测点n3～n7在y方向最大振幅随剪切率的变化曲线。可见：随剪切率的增加，监测点y方向最大振幅逐渐增大，当剪切率为0.05时，监测点y方向振幅达到最大值，随后在y方向振幅开始减小。这个现象是由于“剪切率锁定”引起的，当剪切率为0.05附近时，虽然此时管受到的流体力不是最大，但是监测点的振动却是最剧烈的。

图7 管束不同位置最大振幅随剪切率变化折线

图8给出了监测点n5随剪切率变化的轨迹，从监测点运动轨迹图可以看出，低雷诺数时，在剪切来流的作用下弹性单管的振动会出现一些规律性现象。可见随着剪切率k的改变，结构的运动轨迹变化较大，单管以‘8’字形轨迹运动；随着剪切率的增大，监测点在顺流方向的振动中心先向下游偏移，当剪切率大于0.05时，在顺流方向的振动中心又回到了上游；随着剪切率的增大，监测点在y方向的振幅先逐渐增大，当剪切率为0.07、0.09时y方向的振幅又开始减小。进一步验证了“剪切率锁定”现象的存在，探究了低雷诺数下剪切率对单管的振动特性影响。

(a)k=0.03

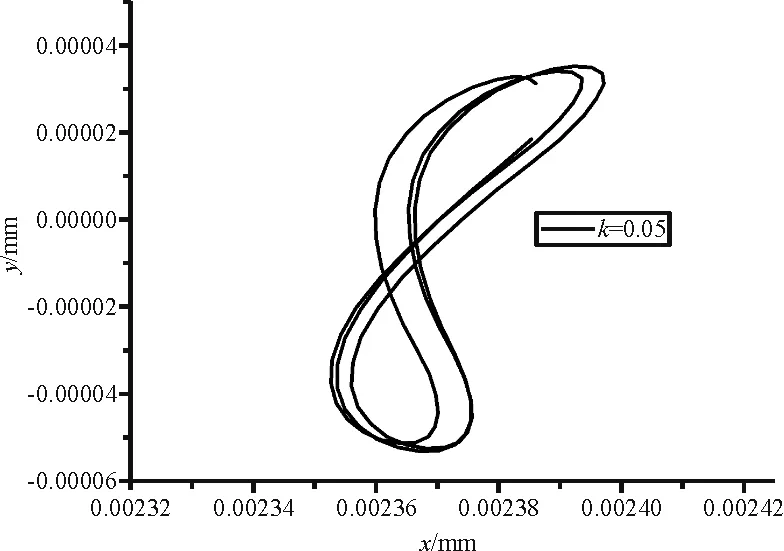
(b)k=0.05

(c)k=0.07

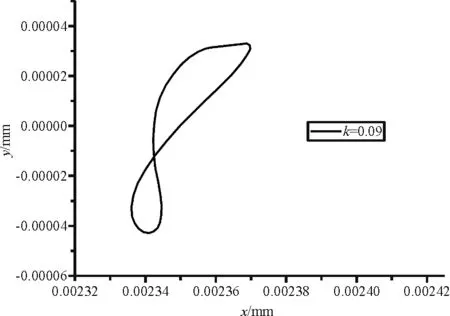
(d)k=0.09

4 结论

本文基于双向流固耦合方法，详细研究了低雷诺数下剪切流作用弹性管的升力系数、监测点的最大振幅、监测点的运动轨迹。结合工程实际，选取剪切率范围为0.01～0.1，通过对升力系数、监测点的最大振幅、监测点的运动轨迹响应的分析和讨论，结果表明：低雷诺数下，剪切率存在类似折减速度的“锁定区间”，受“剪切率锁定区间”的影响，单管的升力系数曲线最大振幅、监测点y方向最大振幅、监测点运动轨迹出现了规律性的现象。

在海洋工程中，海底设备的管线和立管长期处于剪切流作用中，为了增加管线和立管的使用寿命，就需要尽可能减少管线和立管的振动幅值和振动频率，在本文参数范围内，当剪切率取值在0.01或0.1附近时，振动幅值可获得相对较小值，这对海洋工程中的管线应用有一定的参考价值。