三维数值波流水槽的构建及验证
崔栗铭
(西南交通大学土木工程学院, 四川成都 610031)
在跨海桥梁的建设过程中,往往面临着复杂的海洋环境,将会遇到风、浪、流的严峻考验。传统的波浪及水流对结构物的作用已有大量学者展开研究并得到了计算方法。而波流联合作用的机理十分复杂,并不能简单地将两者进行迭加而得到。计算机数值模拟的方法由于其不需实验费用,且可视化程度较高,因此很多学者采用数值方法对流体作用进行研究。其中T·Kawamura[2]运用大涡模拟研究了穿透液面的圆柱绕流;Jungsoo Suh[3]研究了气液交界面对圆柱绕流漩涡脱离的影响;康啊真[4]建立了三维波浪与结构物相互作用的数学模型;冯谊武[5]通过CFX研究了围堰所受波浪荷载。目前关于波流场的数值模拟,主要方法有利用边界条件造波造流法、质量源法。李勇[6]基于RANS方程,使用边界造波和边界入流相迭加的方法实现数值波流场的模拟;康啊真[7]基于LES建立了三维波流与结构物相互作用的数值模型;Li[8]建立了二维数值水槽来计算波流作用下淹没圆柱的水动力系数。
本文使用数值计算软件Fluent,基于Reynolds平均的Navier-Stocks方程,以及速度入口造波造流的方法模拟波流联合作用,并使用动量源项对下游波流场进行消波,通过考察波浪传播的完整性和规则性,以及沿水深的时均速度分布验证了数值水槽的合理性。
1 数值计算理论
现有的流体数值计算理论基础主要包括两类,一是基于势流理论,二是基于粘性流体理论。其中基于势流理论的边界元法被广泛应用于波浪与浮体的相互作用问题,但是势流方法忽略了流体粘性,而本文需要模拟波流联合的结构物作用,因此采用基于粘流理论的计算软件Fluent,并基于雷诺平均的NS方程(RANS)建立波流联合作用数值水槽。其控制方程主要如下。
雷诺平均方程的质量守恒方程以及动量方程分别如下:
(1)

(2)
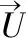
对于湍流较强的数值模型,在Fluent中常采用k-ω或k-ε模型,传统的两方程模型k-ω模型更适用于存在逆压梯度的边界层问题,而k-ε模型能更好地模拟远离壁面处的充分发展的湍流流动。k-ωSST湍流模型结合了k-ε和k-ω湍流模型两者的优势,在近壁面处保留原始的k-ω,在远离壁面处采用k-ε模型。k-ωSST湍流模型的控制方程如下:
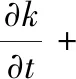
(3)
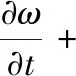
=αS2-βω2-(F1-1)CDkω
(4)
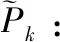
(5)
(6)
(7)
湍流粘度定义为:
(8)
S为应变速率的不变量:
G=2vTSijSij
(9)
F2为混合函数:
(10)
αi=α1F1+α2(1-F1)
(11)
βi=β1F1+β2(1-F1)
(12)
其中系数αk1=0.85034,αk2=1,αω1=0.5,αω2=0.85616,γ1=0.5532,γ2=0.4403,β1=0.075,β2=0.0828,β*=0.09。
2 计算方法及初始条件
Fluent采用有限体积法对控制方程进行离散,本文采用基于压力求解的瞬态计算方法,瞬态格式采用一阶隐式,湍动能和紊动能耗散率采用一阶迎风,并采用PISO算法进行迭代计算。对于自由液面的追踪,采用流体体积方法(VOF),计算初始条件将水体定义体积分数为1,水面以上部分体积分数定义为0,纯流及波流工况下,定义整个水体部分初始流速Uo。对于纯波工况,除了湍动能和紊动能耗散率定义为小值,其余均为零。
3 边界条件的设置
为了建立水槽模拟波流联合作用,本文采用速度入口方法进行造流与造波,即在水槽的上游边界通过用户自定义函数输入波流联合作用下的速度函数来造波流,在下游通过明渠出口边界条件使水流自由流出,其中各个边界的设置及物理意义分别如下。
两侧边界:采用对称(Symmetry)边界条件,沿该边界法向,速度为零,所有物理量梯度为零。
顶部边界:采用压力出口(Pressure)边界条件,满足动力学边界条件,表面压力为大气压力Pa。
底部边界:由于随着时间变化,底部边界的紊动会从边壁向上部扩散, 形成充分的紊流,因此底部边条件设置为不可滑移墙边界(Wall),壁面粗糙度为常数0.5。
上游边界:对于波流工况,采用速度入口边界(Velocity-inlet)输入波流的速度分布函数,设置x,y方向速度为波流作用下的水平速度ux和竖向速度uy,z方向的速度设置为0,同时由于入口边界的液面会随波面的变化而变化,因此还需要自定义液面体积分数函数Wavesurface。波流作用的速度ux,uy,以及液面体积分数函数Wavesurface公式如下所示:
(13)
(14)
wavesurface=H/2·sin(k·x-σ·t)
(15)
其中:Uo为纯流流速;H为波高;k为波数;d为水深;σ为波频;z为沿水深方向高度;C为波速。
下游边界:将下游出口边界设置为压力出口(Pressure-outlet),并打开明渠流设置(Openchannel),边界的压力判别方法采用自由液面(FreeSurfaceLevel)判别,出口边界的体积分数采用相邻单元的体积分数,边界的静压及总压计算方法如下:
(16)
(17)
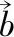
源项消波:为了避免下游波浪反射影响,因此设置消波条件,采用源项消波,通过在消波段定义动量源x_source和y_source来进行消波,其中:
con=C_R(c,t)·(x[0]-x1)/(x2-x1)·θ1
(18)
纯波:x_source=-C_U(c,t)·con
(19)
波流:x_source=(C_U(c,t)-Uo)·(-con)
(20)
y_source=-C_V(c,t)·con
(21)
C_R(c,t)为水槽消波段任意水质点的密度;Uo为波流工况中均匀流流速;C_U(c,t);C_V(c,t)为水槽消波段任意水质点的x,y方向速度;源项消波阻尼参数θ1=2~4。
4 水槽品质检验
为了对数值水槽进行验证,因此建立数值模型与其他学者所做数值水槽及实验进行对比,本文数值验证采用与李勇文章中相同的工况进行验证,计算域为xyz=36m×0.8m×0.5m。模型边界条件及网格划分方式如图1所示,分别在液面高度和靠近水槽底部处进行网格加密,而在速度入口一个波长范围也同样进行网格加密,这样做的目的分别是为了更好的捕捉液面,更好地模拟水槽底部的剪切作用使得沿水深方向的速度分布更加接近于实际,以及防止在造波边界处出现波浪破碎。波浪工况采用李勇文章中的波流工况,同时也是Van Rijn[9]实验中的工况,工况波浪参数如表1所示。
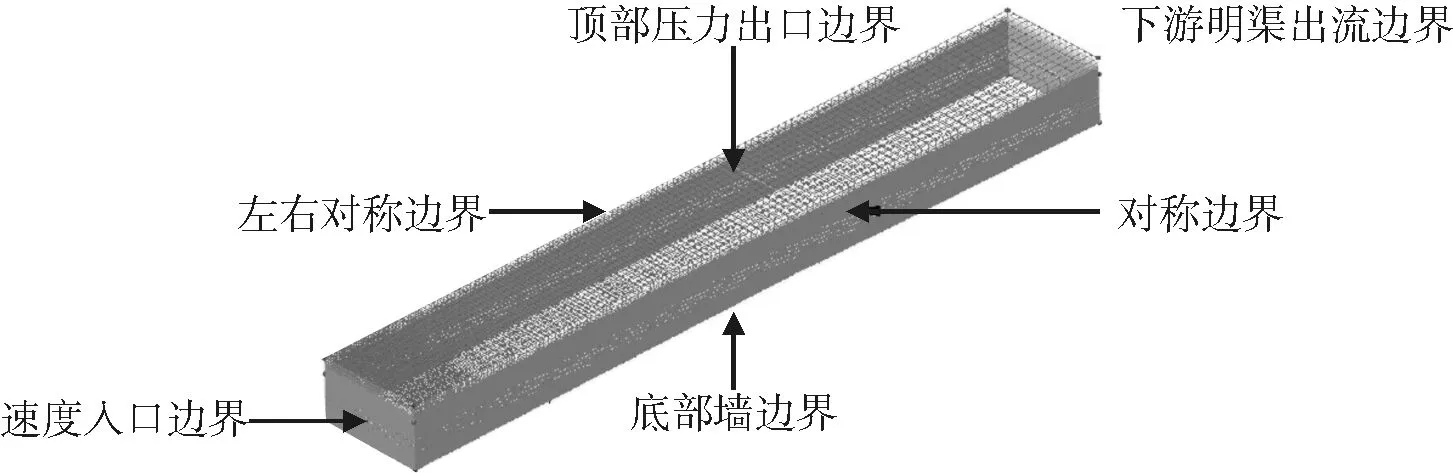
图1 模型边界

表1 Van Rijn实验条件
考察数值水槽的品质是否优良,需要考察水槽波浪变化是否规则,波浪传播是否完整,因此需要知道水槽瞬时的三维波面变化情况。根据Mehaute波浪理论选择的判断方法,判定工况中的波浪参数非线性较强,且水深较浅,因此采用椭圆余弦波浪理论较为合适。从图2中也可以看到,三维数值波面传播完整且规则,呈现波峰高窄而波谷缓长的形式,说明波流联合作用下的波浪形态模拟较好。
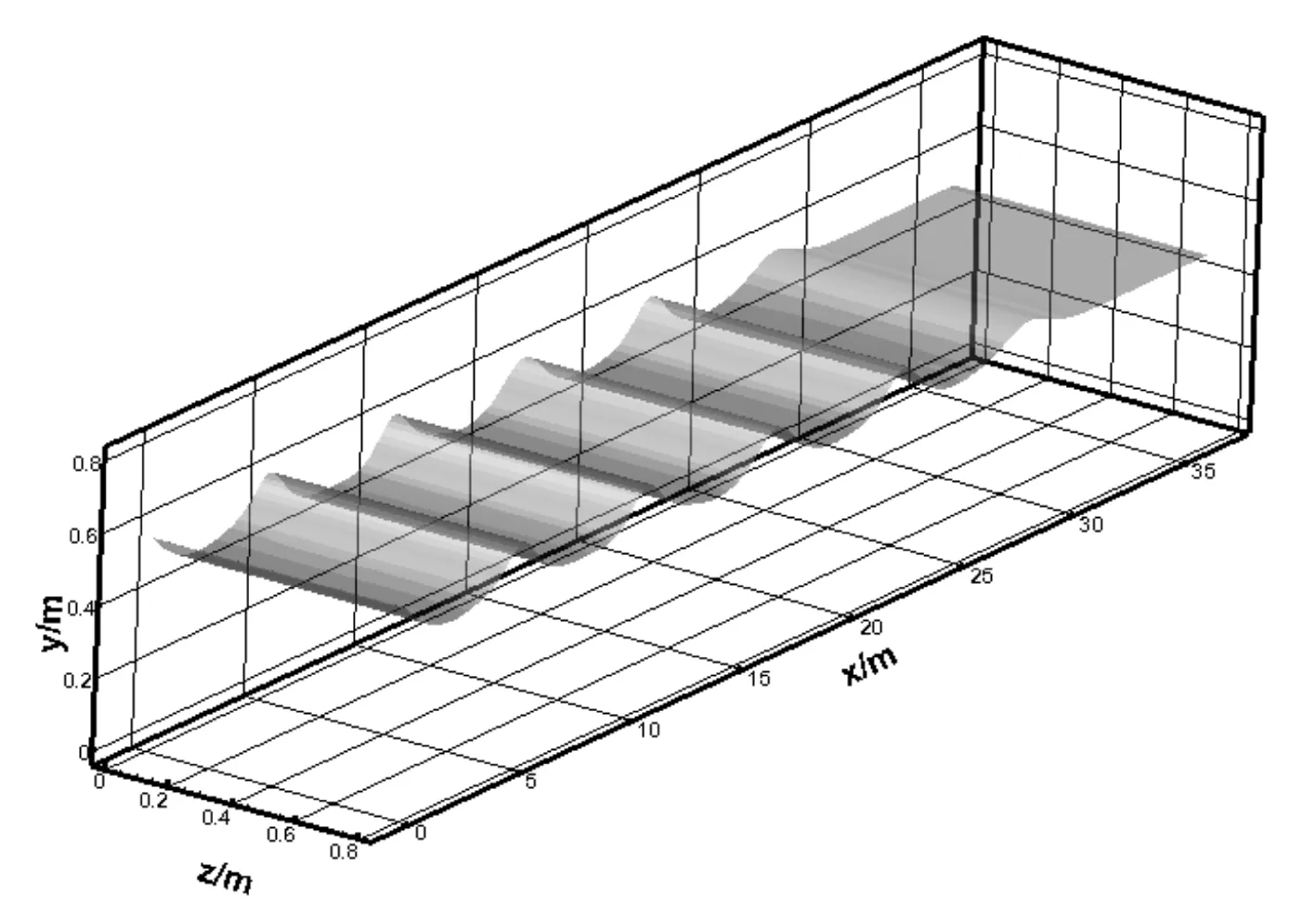
图2 三维瞬时波面
再对水槽波面变化情况进行考察,由于波流水槽中需要满足水槽下游反射波浪对上游无影响,且水槽内流量守恒,因此需要在尾部进行消波,并且需要波面无抬升。由图3波流水槽波面变化图可以看出,随着波浪进入消波区域,波高迅速衰减至静水面位置,且无反射波的出现。同时在水槽中四个波浪的波高不随位置的改变而衰减,说明没有发生数值耗散,在整个水槽中波浪都保持非常完整的形态。同时也可以看出,四个波高没有产生依次的增高,说明整个水槽内流量保持守恒的状态,在下游边界,水流可以自由地流出。
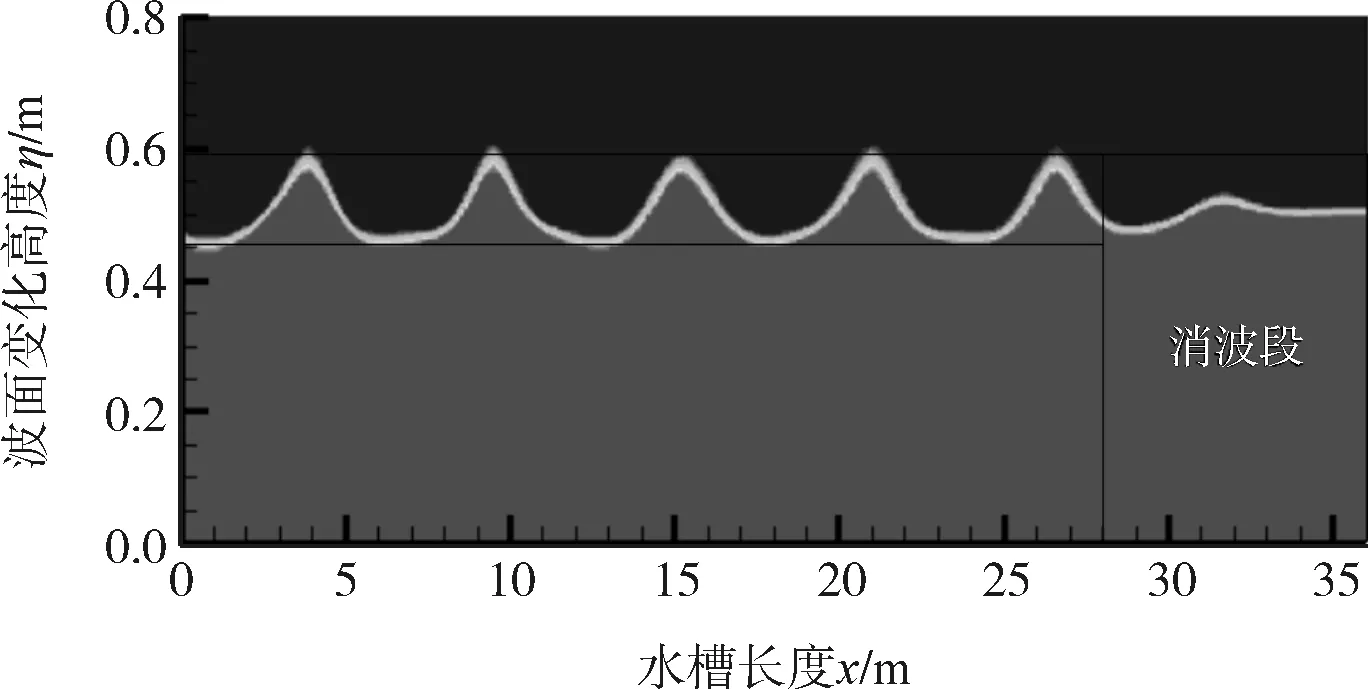
图3 波流水槽波面变化
再对数值水槽中的速度分布进行考察,由于建立的波流水槽在消波前的区域为波流联合作用,而在消波区为了消除波浪的反射等,因此需要通过源项消波使下游区域到出口边界逐渐由波流联合形态转变为纯流形态。因此由图4水槽速度云图可以看出,在消波区域之前,由于波流作用,使得在波浪位置处,速度变化较为剧烈,能量主要聚集在四个波浪位置处,而进入消波区域后,随着波浪的消减,波面变得平静。而在靠近下游边界的地方,整个水槽深度方向速度变得一致,说明由于动量源项的作用,使得水体沿深度方向变成了速度一致的均匀流。
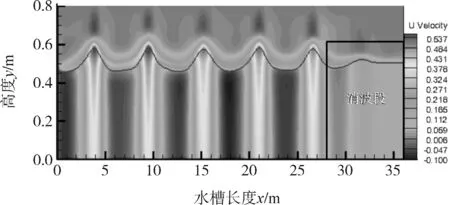
图4 水槽速度云图
最后再对水槽中不同位置处沿水深方向的速度分布进行比较,将x=4 m、5.5 m、8 m、11 m、15 m、20 m位置处的速度进行时间平均,然后与李勇建立的水槽速度分布以及其他学者实验中的数据进行对比。由图5可以看出,在中上游位置处,流速的分布比较稳定,流速变化趋势基本一致。在水深0.2 m以上位置,本文建立水槽速度分布介于纯流以及波流实验之间,在水深0.05~0.2 m之间,本文与李勇所构建水槽速度分布及波流实验数据较为一致。而在0.05 m位置以下,本文速度分布与李勇及纯流实验数据较为一致;在靠近下游x=15 m、20 m位置处,可以看出流速相对中上游位置速度分布发生较大改变。在水深0.05 m以上位置,流速逐渐减小,而在底部位置,速度分布变化相对较小,整体更趋向于均匀分布,说明在靠近于下游位置处,由于消波区域的影响,使得流速分布更加趋向于均匀流。
总体而言,本文所建立数值水槽在能够保证波流联合作用下波浪要素的完整性,并不发生数值耗散,同时水槽中流量守恒,并没有出现波面的抬升。同时下游消波段能够完整消波,使得消波区域的流体形态由波流转变为均匀流。整个水槽沿水深的速度来看,在中上游位置处,水槽速度分布介于纯流及波流实验数据之间,在靠近下游消波段位置处,流速分布受其影响,更加趋近于均匀流,只要将结构物放置在远离下游的位置处,可以忽略下游对上游的影响,因此本文所建立水槽能够较好模拟波流联合作用。
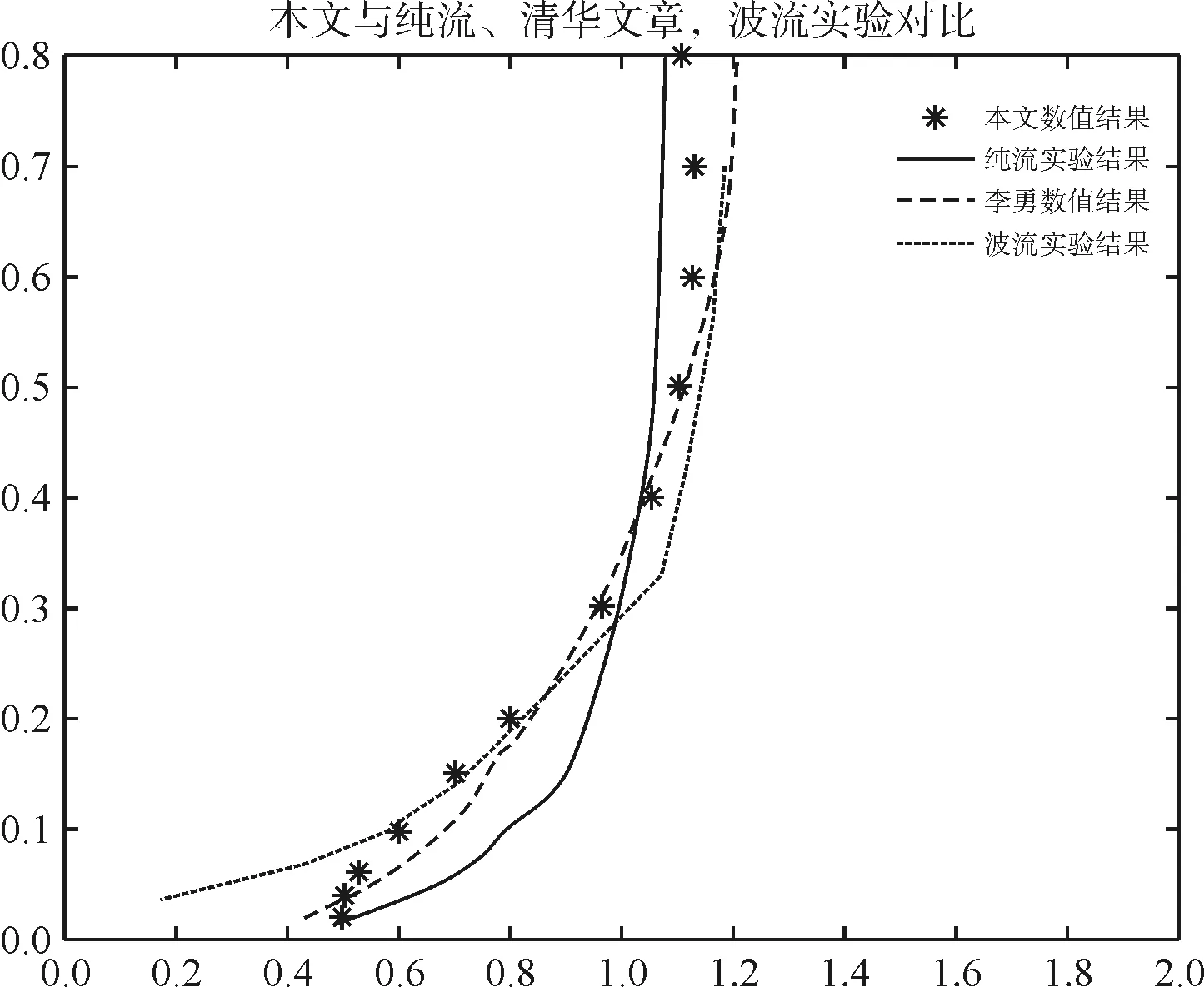
(a)x=4m

(b)x=5.5m
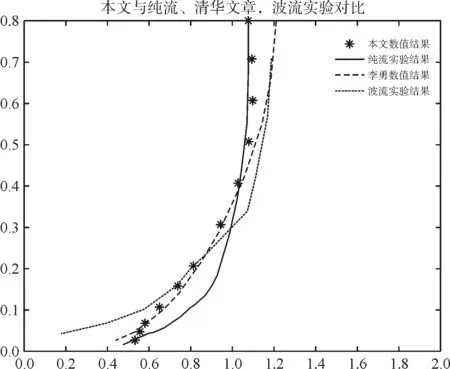
(c)x=8m
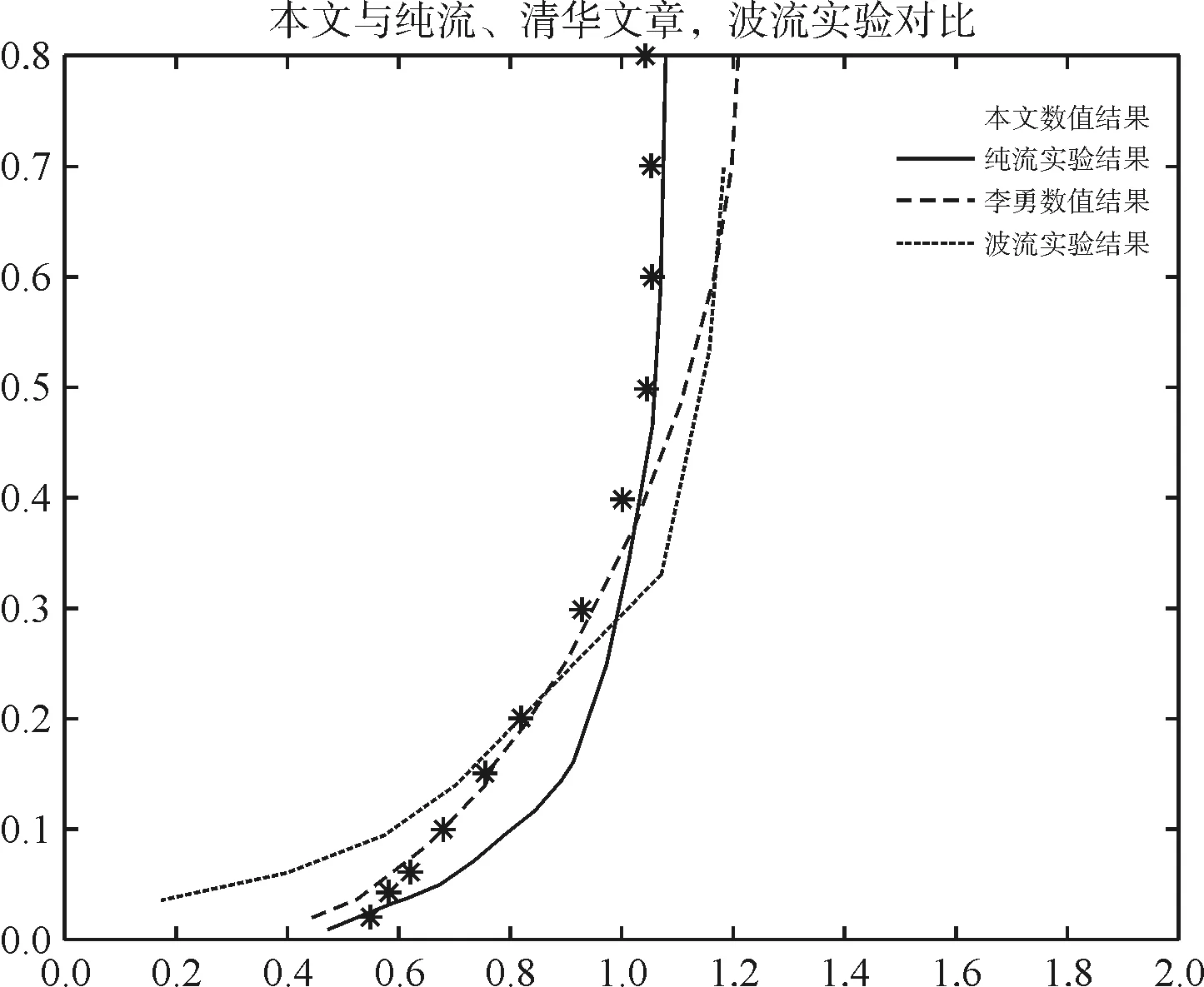
(d)x=11m
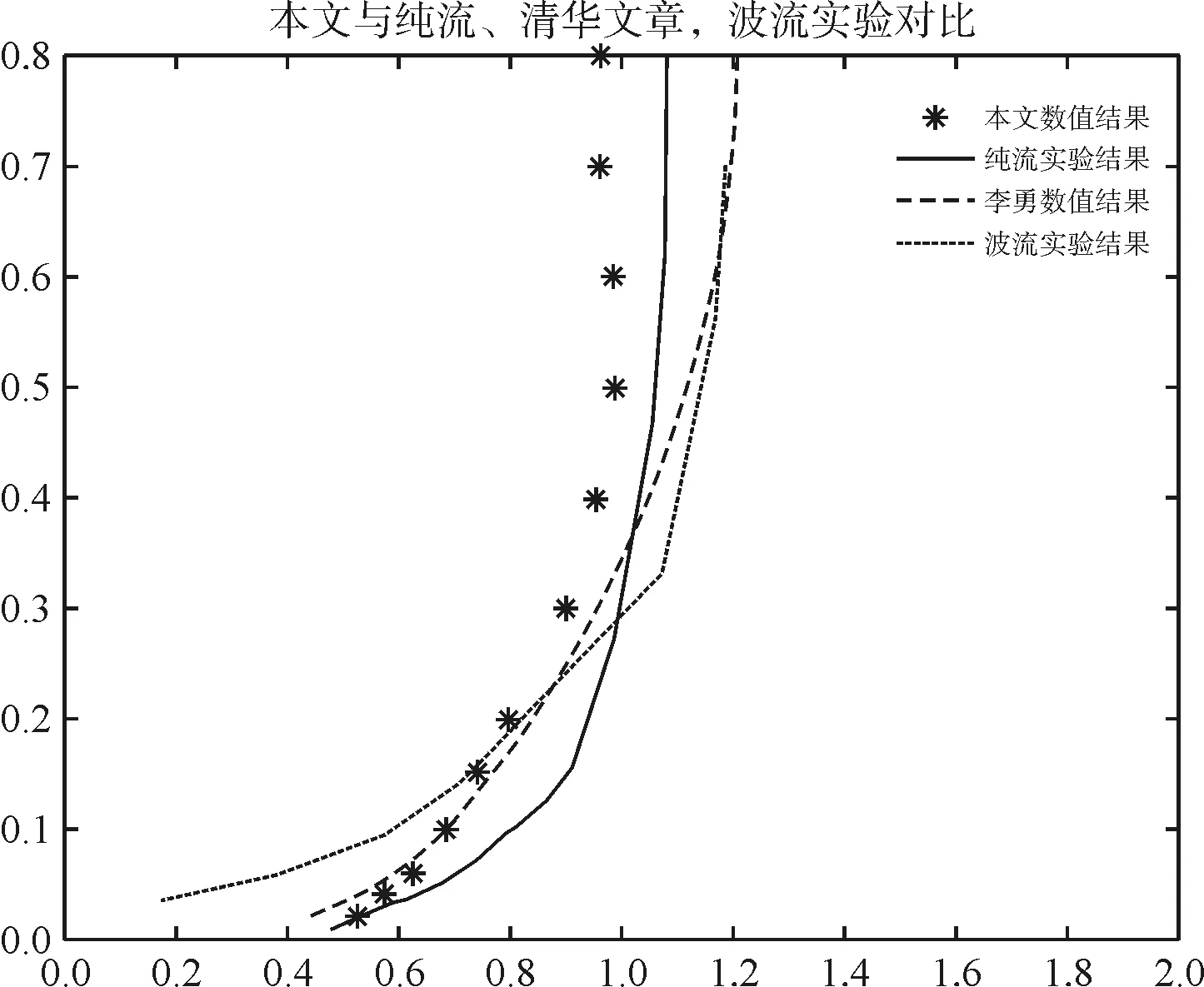
(e)x=15m
(f)x=20m图5 x=4m、5.5m、8m、11m、15m、 20m处沿水深方向速度分布对比
5 结论
本文采用边界造波和造流方法所得到的三维数值水槽模型,经过液面变化形态考察和速度分布定量对比两方面,验证了数值水槽消波的效果以及流场中速度分布与实际情况的吻合程度。从瞬时三维波面变化图以及二维液面变化图得出,水槽造波完整且稳定,并且水槽内部流量守恒,液面无抬升,消波效果迅速,在消波段内,流场形态由波流联合作用场迅速消减为均匀流场。从时均速度分布对比图中可以看出,在中上游位置,流速分布介于纯流实验及波流实验数据之间。总体而言水槽流速分布与实际情况吻合较好,靠近消波段位置的流速分布受消波效果影响,沿水深上部流速降低。因此在研究波流联合作用时,应考虑中上游位置的流场,且结构物应远离下游消波段。综上所述,本文所建三维数值水槽对于波流联合作用下的流场形态模拟较好,波浪传播稳定,参数完整,且无反射波的影响。

