对《平均相对分子质量对化学平衡判断的数学证明》一文的商榷
李建涛

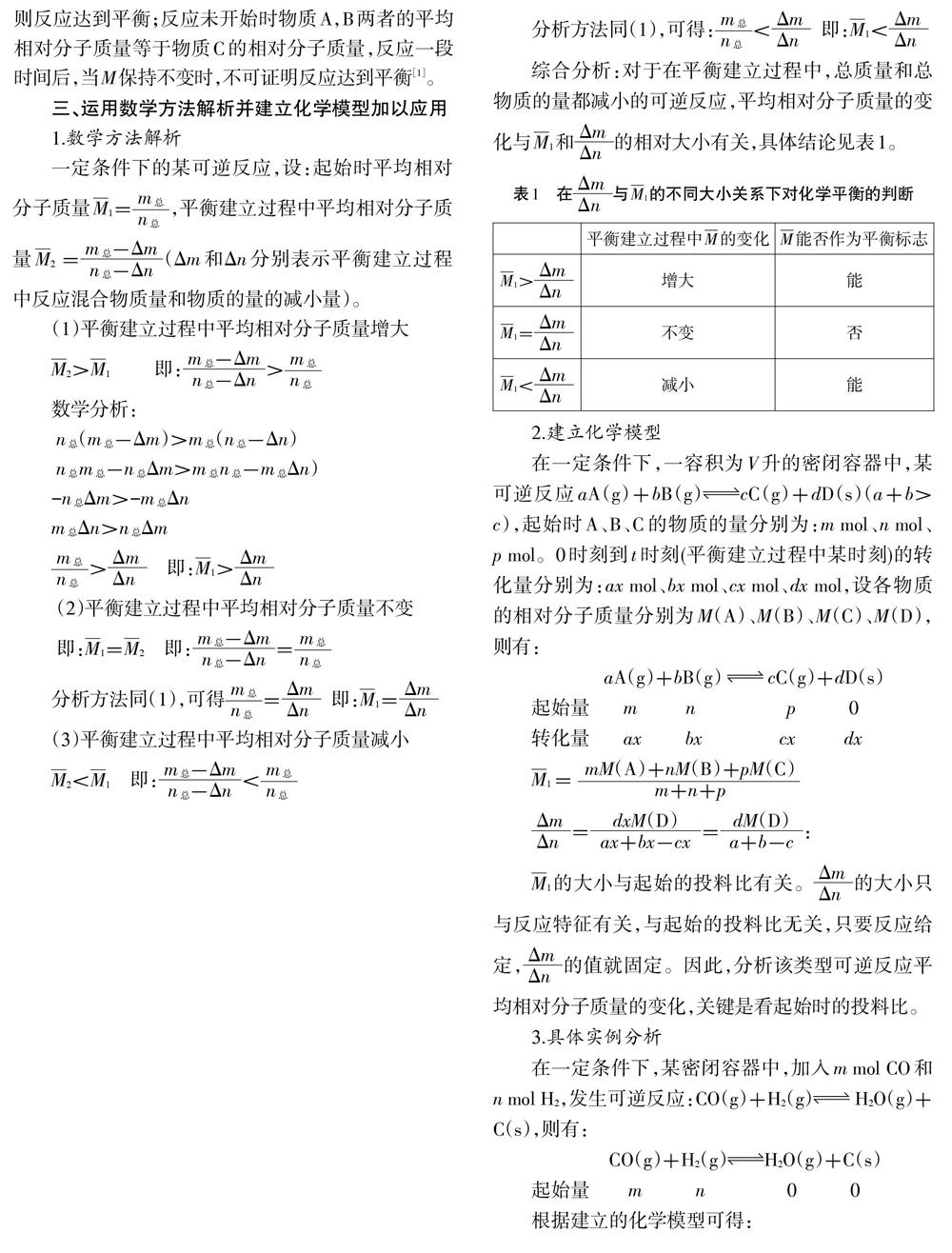
摘要:建立模型,從另一个角度运用数学方法解析和探究“在m(总)、n(总)同时向一个方向改变的过程中,平均相对分子质量能否作为平衡标志”,最终得出结论并应用。
关键词:数学解析;平均相对分子质量;化学平衡
文章编号:1008-0546(2019)06-0024-03 中图分类号:G633.8 文献标识码:B
doi:10.3969/j.issn.1008-0546.2019.06.007
化学教与学2017年第10期《平均相对分子质量对化学平衡判断的数学证明》一文(以下简称该文),该文系统探究化学平衡的判断方法,总结全面、详细,并从数学角度来证明平均相对分子质量对化学平衡的判断,分类讨论,并以函数图像形式呈现,形象直观,思路新颖,是难得一见的好文。但是,笔者发现该文“数学证明部分”存在一定的局限性,结论存在一定偏差,不具有普遍性。
二、存在的局限性和偏差
1.建立的模型不具有普遍性,假设的具体值太多,如A、B相对分子质量的值、反应起始投料比等于反应物化学计量系数之比等,这就使最终得到的结论要受到本身假设条件的限制,具有一定局限性。
2.利用公式2证明过程中,反应起始投料比等于反应物化学计量系数之比,在平衡建立过程中,反应物物质的量之比始终不变,物质A、B两者的平均相对分子质量始终不变,如果起始投料比不等于反应物化学计量系数之比,在平衡建立过程中,物质A、B两者的平均相对分子质量始终变化,此结论就无法应用。
基于以上,笔者尝试运用数学方法从另一个角度分析,重新建立模型,探究“在m(总)、n(总)同时向一个方向改变的过程中,平均相对分子质量能否作为平衡标志”。
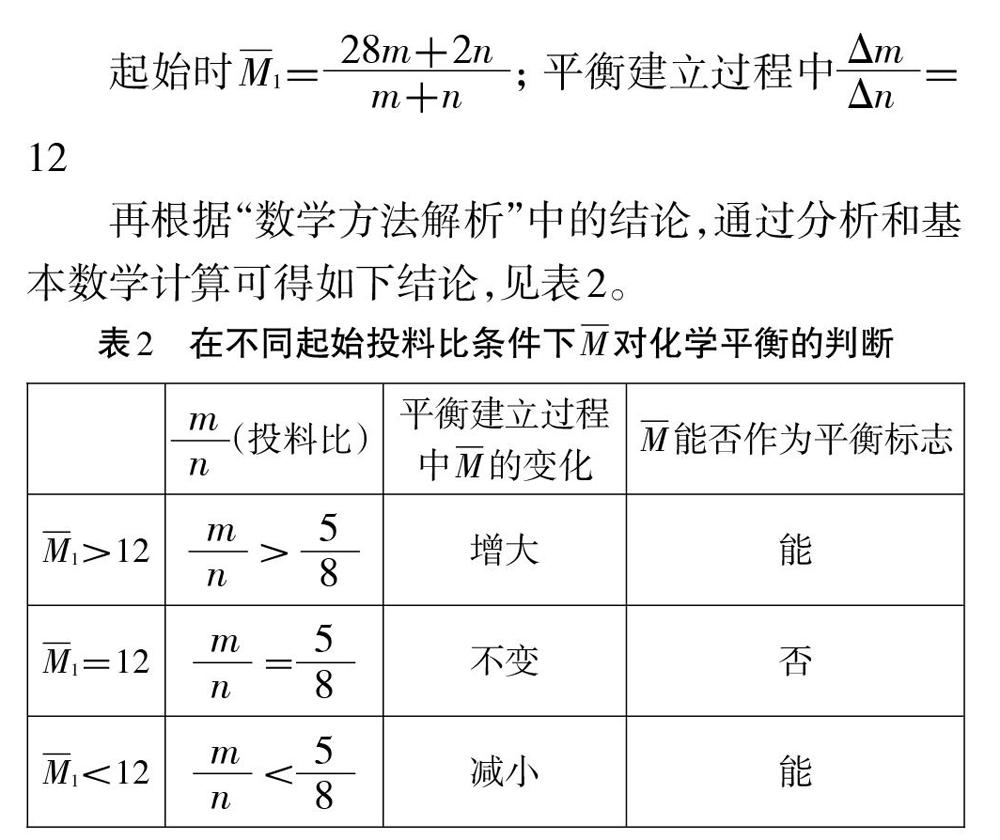
再根据“数学方法解析”中的结论,通过分析和基本数学计算可得如下结论,见表2。
四、启示
我们在用数学方法解析化学问题时,建立的模型要具有普遍性,解析过程中,应用的物理量及其变量不宜过多,要控制变量,尽量不要将一些化学常数赋予具体值,这样通过数学分析得出的结论,更具有应用的价值。

