基于两阶段启发式算法的多目标外卖配送优化分析
徐肇元
(山西农业大学 软件学院,山西 太谷 030800)
0 引 言
随着人们生活水平的提高和互联网的发展,新兴的网络订餐模式——外卖由于其便捷性,越来越受到人们的认同.当前主流的销售方法是通过O2O的形式,即顾客通过订餐平台下单,商家通过线下配送的方式送货上门.外卖配送作为外卖的基础业务,如何提高送餐效率,降低送餐成本是其重要的问题[1].在商家进行外卖配送的过程中,过早或过迟到达,顾客的时间满意度都会受到影响[2].外卖配送线路优化问题被认为是一种准MDVRPTW(带时间窗的多车场车辆路线问题).该问题需要同时满足外卖配送和MDVRPTW的要求[3].其中VRP是由Dantzig和Ramser在1959年提出来的一种NP-hard问题[4],是指基于一个或多个中心、汽车集和客户集,在满足约束条件的前提下使其线路最优的问题.现用来解决VRP的算法有遗传算法[5]、蚁群算法[6]、粒子群算法[7]和节约算法[8]等.易彩玉[9]研究了如何使用联合调度,以解决预约和即时两种模式下的外卖生产配送的问题;王荃菲[10]对基于商家自营外卖配送服务和订餐平台配送服务的两种不同的模型,设计了不同的配送路径方案;陈萍[11]等人提出了一个适合餐饮O2O外卖配送的优化模型并利用一种改进的遗传算法进行求解.本文对基于客户时间满意度和配送总成本的多目标外卖配送线路优化模型进行深入研究,以最大化客户满意度为主要目标为商家提供了线路规划方案.
1 模型的建立
在模型建立之前先定义二进制决策变量:
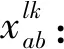

1.1 问题假设
1)商家各门店拥有的外卖车数量足够外卖配送员使用;
2)每辆外卖车型号相同,载重量是固定的;
3)每辆外卖车从商家的某门店出发,完成配送任务后回到该门店;
4)每辆外卖车保持匀速行驶,不受路况环境的影响;
5)每个外卖订单仅被一个外卖配送员配送.
1.2 时间满意度
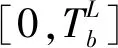
每进行一次外卖配送,都会打开一次外卖配送箱.每次打开都会对箱中不同的食物品质产生影响.假设配送箱中共有v种不同的食物[12],每次打开外卖配送箱对客户b外卖的时间满意度影响值为μb.客户时间满意度

(1)
式中:η为系数且η∈(0,1];δ为指数;r为打开外卖箱的次数.
该商家的客户时间满意度可以表示为
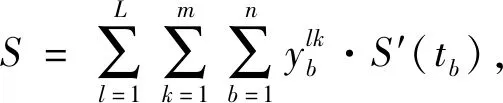
(2)
式中:L为门店的数量;m为外卖车的数量;n为外卖订单的数量.
1.3 配送总成本
商家在进行外卖配送时需要考虑配送的总成本[13],配送总成本主要包括固定成本、运输成本和货损成本.
固定成本为商家每日需要支付给外卖配送员的工资等.其函数表示为
E1=p·Efixed,
(3)
式中:p为外卖配送员的人数;Efixed为商家每日支付给每个外卖配送员的工资.
运输成本为运输过程中的能源消耗成本.该成本与运输距离有关.其函数表示为
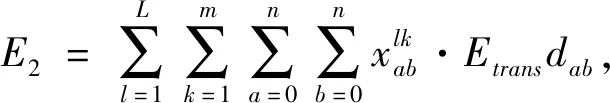
(4)
式中:Etrans为运输过程中单位路程的能源消耗成本;dab为客户节点a到节点b的距离.
此外,在进行外卖配送时,随着运输时间的增加,外卖的质量和温度不断下降.货损成本函数表示为

(5)

配送总成本为
E=E1+E2+E3=
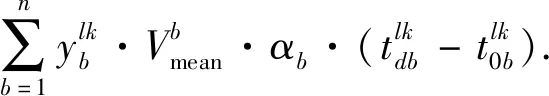
(6)
1.4 模型构建
本文对该多目标问题采用主要目标法[14]进行求解,以最大化客户时间满意度为主要目标,最小化配送总成本为次要目标.其多目标外卖配送路径优化模型为
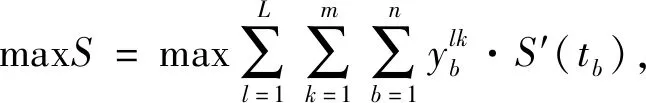
(7)
minE=min(E1+E2+E3).
(8)
约束条件为
所有的外卖订单都被配送到位,
配送路径的数量不超过外卖配送员人数,
每个外卖订单仅被一个外卖配送员配送.
2 两阶段启发式算法设计
本文采用两阶段启发式算法进行线路优化.第一步采用基于就近分配原则的SWEEP算法将多门店问题转化为单一门店问题进行求解,降低问题的复杂性,提高求解效率;第二步使用改进的蚁群算法对多个外卖配送员的配送线路进行优化.
2.1 SWEEP配送区域划分算法
SWEEP算法是由Gillett和Miller提出来的一种启发式算法[15],其本质是将距离相对近的客户节点归并在一条线路中.本文利用改进的SWEEP算法对各门店配送区域进行划分以降低计算问题的复杂性.
算法步骤:
1)比较商家各门店和客户节点的最近距离和次近距离

(9)
式中:o1为离客户节点a最近的门店;o2为离客户节点a次近的门店;dao1为客户节点a和门店o1之间的距离;dao2为客户节点a和门店o2之间的距离.
当0≤r(a)<λ时,客户节点a由门店o1进行配送;当λ≤r(a)≤1时,该节点a为边界点,λ∈[0,1];
2)对所有的n个客户节点进行第1步的判断,得到门店A,B,C…的配送集WA,WB,WC…;
3)基于已得到的配送集对少部分边界客户节点进行门店的分配.分别在某边界客户节点a最近和次近门店对应的配送集Wo1,Wo2中选择距离客户节点a最近的客户节点bo1和bo2,比较两者相对距离
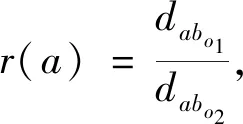
(10)
式中:dabo1,dabo2分别为客户节点a到节点bo1和bo2之间的距离.
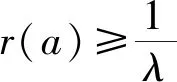
2.2 改进蚁群算法
蚁群算法已广泛应用于多个领域.但该算法存在着收敛速度慢、常出现搜索停滞现象和易陷入局部最优等问题.本文通过对蚁群算法进行改进可以有效地解决上述问题,增强算法实用性和提高算法性能.
2.2.1 伪随机比例状态转移规则
蚁群系统(ACS)由M.Dorigo在1996年提出[16],主要改进是采用了伪随机比例状态转移规则[17].在ACS算法中,伪随机比例参数q0反应了蚂蚁利用已有知识和探索新知识的相对性.当 0≤q≤q0时,蚂蚁进行确定性搜索;当q0 Select= (11) 改进伪随机比例状态转移规则参数q0.令 其中,q0_min为伪随机比例参数q0的最小值,υq0为参数变化函数系数.在算法前期,参数q0取值较小,有较大概率进行随机搜索,有利于发现更优解;在算法后期,参数q0取值较大,有较大概率进行确定搜索,缩短算法运行时间,加快收敛速度. 2.2.2 信息素更新规则 蚁群算法中信息素的更新可分为全局更新和局部更新两部分.在全局更新中,基本算法对所有路径都执行信息素更新,包括较差路径,这会降低最优路径被搜索到的可能性,易造成算法振荡,陷入局部最优解.对全局信息素更新规则进行改进,通过正负反馈方法更新至今最优路径和最差路径上的信息素,提高全局最优解搜索能力,加快算法收敛速度. 全局信息素更新公式为 τab(t+n)=(1-ρ)·τab(t)+Δτab, (12) (13) 式中:ρ为全局信息素挥发系数;Q为全局信息素增量系数;Sbest和Sworst为至今最优和最差路径客户时间满意度;Snext-best和Snext-worst为至今次优和次差路径客户时间满意度;Sbest-ave和Sworst-ave分别为至今多次迭代最优和最差路径的平均客户时间满意度. 2.2.3 引入局部搜索算法 k-opt去交叉算法是由Croes提出来的一种局部搜索算法[18].该算法是基于邻域的概念,在局部最优解的邻域中寻找更好的解,如果有则替换当前的解.本文利用2-opt算法对局部最优解进行优化,可以创造大量有较大差异的可行解,一定程度上避免更优的解丢失,克服其陷入局部最优. 2)将μ只蚂蚁随机放到p个节点上; 3)构造每只蚂蚁未访问的节点To_visit和已访问节点Visited,遍历所有节点,利用路线转移和伪随机比例转移规则选择下一个客户节点或是回到门店,并将节点加入Visited中,最后所有配送点全部被访问,更新禁忌表; 4)记录当次迭代参数并应用2-opt算法更新局部最优解,记录至今最优、次优、最差和次差路径; 5)根据全局信息素更新规则更新信息素矩阵Tau; 6)达到预定的迭代次数N_max时,结束循环,否则跳转到第2步. 假设某商家共有门店2家,单日订单数为25个,根据建立的多目标外卖配送路径优化模型,利用如上算法设计求解.其中:外卖车最大载重量为8 kg,行驶速度为20 km/h,各客户节点配送等待时间为3 min,每日每位外卖配送员固定支出Efixed为3元/人,时间满意度系数η为0.4,指数δ为2,运输过程中单位路程能源消耗成本Etrans为1.2元/公里.在实例分析时两个客户节点间的配送路程使用直线距离,门店和客户节点对应其他数据参数如表1 所示. 该商家以最大化客户满意度为主要目标,在进行路径规划时,其规划方案为:门店A负责9个订单的配送,需要2个外卖配送员,其配送路径为:0-5-4-8-11-1-0,0-23-2-7-3-0;门店B负责16个订单的配送,需要4个外卖配送员,其配送路径为:0-11-14-10-9-5-12-0,0-4-3-2-8-7-0,0-6-13-15-16-0,0-1-0.此时该商家客户时间满意度为96.49%,配送总成本为82.64元.此外,商家还可以设置配送总成本的最高限制,在有限配送总成本的条件下达到客户满意度的最大值. 表1 门店和客户节点相关数据参数表Tab.1 Related data parameter table between store and customer node 本文建立了关于客户时间满意度和配送总成本的多目标外卖配送路径优化模型,并利用两阶段启发式算法进行求解,在将客户时间满意度作为主要目标的前提下为外卖商家设计了规划方案.本文在建立模型时,分别将客户时间满意度和配送总成本作为目标分析,符合外卖商家客户第一的要求,对外卖配送路径规划具有一定的指导意义.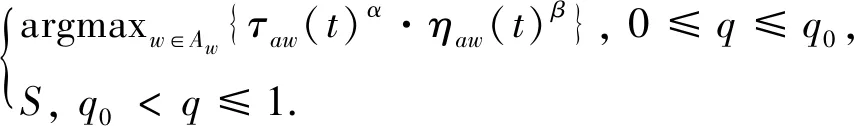
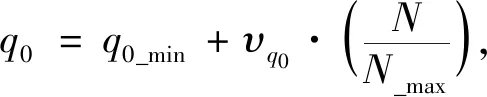

2.3 算法步骤
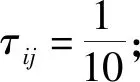
3 实验结果与分析

4 结 论

