基于模型参考自适应的永磁同步电机矢量控制

李梦瑶，孙逢春，何洪文

(北京理工大学 机械与车辆学院，北京 100081)

0 引 言

永磁同步电机(PMSM)具有强非线性、强耦合、多变量、时变等特点，需要选择合适的控制策略以提高系统的稳定性、快速性和鲁棒性.永磁同步电机的矢量控制是将定子电流分解为励磁电流分量和转矩电流分量，实现解耦控制.因其动态响应速度快、可靠性高、调速范围广、转矩控制精准等优点，成为目前应用最为广泛的电机控制策略之一.矢量控制在控制过程中，转速、电流双闭环的控制结构须通过转子速度和位置检测实现[1].测量电机转子的速度和位置，一般需要在转子的转轴上安装旋转变压器、感应电机、光电编码器、霍尔传感器、磁性编码器、测速发电机等机械式的传感器，增加了系统的硬件成本以及后期维护量，降低了系统的可靠性.为克服机械传感器带来的局限，很多学者开展了对无传感器控制技术的研究.无传感器控制的基本思想是利用电机绕组中的相关电信号，通过适当的方法估算出转子的转速和位置.目前PMSM无传感器控制策略主要包括基于模型的中高速控制方法和以高频注入法为主的低速控制方法，以及结合两种方法优点的混合控制方法.

高频注入法的基本原理是在电机中注入特定高频电压(电流)信号，检测电机中对应的电流(电压)信号，通过一定带宽的滤波器来提取转子信息.这种方法要求电机具有凸极效应，适合于内置式永磁同步电机.由于系统依赖外加高频激励信号来显示凸极性，所以采用高频注入法的控制系统对电机参数的变化不敏感，位置观测精度高，可用于低速和零速的速度估计.但在转速较高时，由于定子电阻和旋转电压不能忽略，高频注入下的简化模型不再适用，因此这种方法不适合高速时的无传感器控制.同时目前的控制策略不能同时提高转子位置的估计精度、降低可闻噪声、简化信号处理，还存在很多不足[2-5].

基于基波数学模型的3相PMSM无传感器控制策略依赖模型中与转速有关的量参数估算.目前常用的算法包括滑模观测器算法、扩展卡尔曼滤波器算法、模型参考自适应算法等.滑模观测器利用滑动模态的概念，用滑模变结构形式设计状态观测器，通过结构变化的高频开关来回切换，使状态的运动点在相平面小幅运动，最终稳定到平衡点.这种方法对参数变化及外部扰动不敏感，系统的鲁棒性强，但是一旦进入滑动模态后，开关导致的时间、空间上的滞后会导致观测值沿着实际值上、下振荡，抖振会影响被估参数的估计精度[6-9].扩展卡尔曼滤波器算法基于线性最小方差估计是一种非线性系统的随机观测器，可以实现参数的在线辨识，在抗干扰和鲁棒性方面具有优势.但该算法涉及负载的递推计算过程，计算量巨大，会影响到它的在线应用，同时算法中的系统噪声和测量噪声矩阵取值不能保证系统在全速区间内收敛[10-13].

模型参考自适应法具有参数自适应功能，算法简单、鲁棒性强、参数估计易收敛、稳态性能优良，在无传感器控制领域得到了广泛的应用.模型参考自适应算法根据PMSM的参考模型和可调模型间电流(磁链)状态量的误差，设计自适应律，使得被估计参数渐进收敛于实际值，具有良好的动态性能[14-17].

本文采用模型参考自适应算法对永磁同步电机转子速度以及位置进行参数估计，并提出一种简化模型参考自适应控制策略.基于传统模型参考自适应算法和所提出的简化模型参考自适应算法，搭建永磁同步电机无传感器矢量控制仿真模型，验证两种控制策略在电机启动、转速突变、负载转矩突变等情况下的系统性能.仿真结果表明简化的模型参考自适应算法可快速、准确估算出电机转子的速度以及位置，抗扰性强，适用于永磁同步电机无传感器矢量控制.

1 永磁同步电机数学模型

永磁同步电机的数学模型通常建立在以下条件基础上：① 永磁体材料的电导率为零；② 转子结构中不存在阻尼绕组；③ 不计铁芯饱和、涡流效应和磁滞损耗；④ 电机磁动势按正弦分布，即忽略磁场中所有的空间谐波；⑤ 各相定子绕组匝数相同且空间位置严格对称.

永磁同步电机在3相静止坐标系下的模型具有时变、耦合等特点，为了便于后期控制器的设计，选择在两相旋转d-q坐标系下建立完全解耦的数学模型，则定子电压方程为

(1)

定子磁链方程为

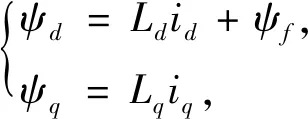
(2)

式中：ud,uq为定子电压的轴分量；id,iq为定子电流的轴分量；R为定子电阻；ψd,ψq为定子磁链的轴分量；ωe为电角速度；Ld,Lq为轴电感分量；ψf为永磁体磁链.电机的机械运动方程为

(3)

式中：ωm为电机的机械角度;J为转动惯量;B为阻尼系数;TL为负载转矩;Te为电磁转矩，电磁转矩方程为

(4)

式中：pn为电机的极对数.对于表贴式永磁同步电机，定子电感满足Ld=Lq=Ls.

2 模型参考自适应系统控制模型

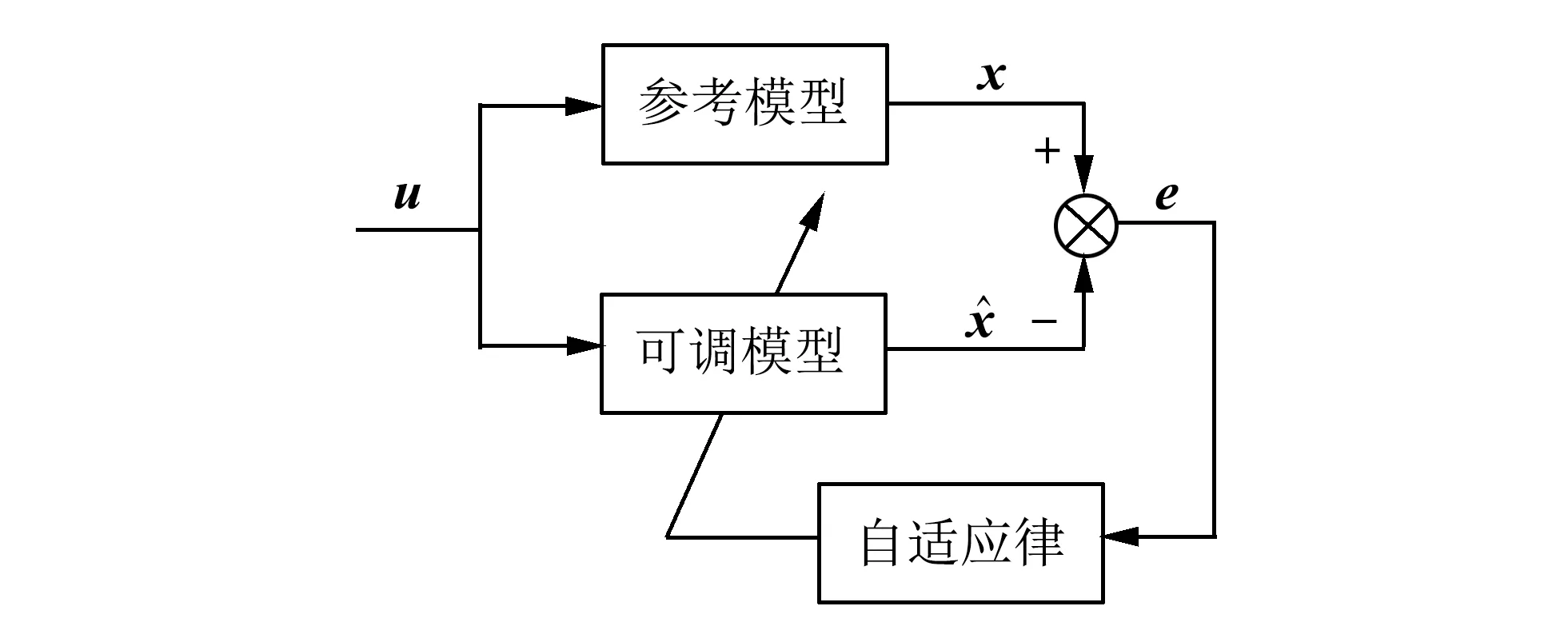
图1 MRAS的控制结构图Fig.1 MRAS control structure diagram

2.1 参考模型与可调模型的确定

在MRAS中，常以3相永磁同步电机的电流方程或磁链方程为参考模型，本文采用电流方程为参考模型.对于表贴式3相永磁同步电机，同步旋转坐标系下的电流方程为

(5)

为获得可调模型，将式(5)变换为

(6)

定义

(7)

则式(6)变为

(8)

改写成状态空间表达式为

(9)

其中，

用估计值表示式(8)为

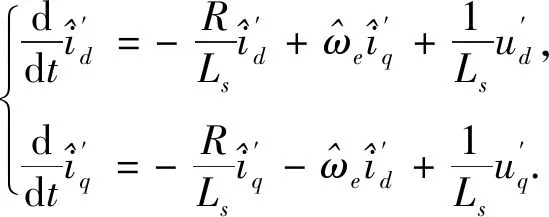
(10)

改写成状态空间表达式为

(11)

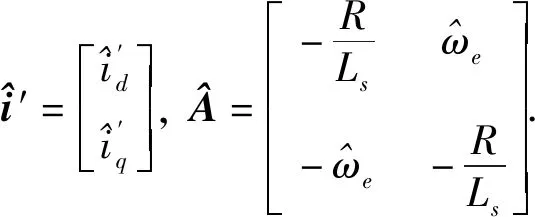
2.2 参考自适应律的确定

(12)

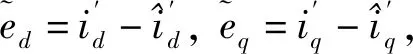
改写成空间状态表达式

(13)

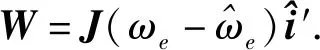
图2 参数辨识系统等效反馈结构图Fig.2 Parameter identification system equivalent feedback structure diagram

根据Popov超稳定性理论，若使这个系统渐进稳定，其中的非线性时变反馈环节必须满足：

1)线性时不变前馈系统的传递函数矩阵G(s)=(sI-A)-1为严格正实矩阵；

2)非线性时变反馈系统满足Popov积分不等式

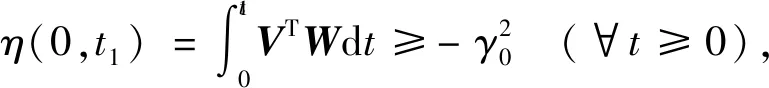
(14)

根据严格正实引理，对于线性定常系统的状态方程

(15)

其传递函数矩阵G(s)=D+C(sI-A)-1B为严格正实矩阵的充分必要条件，存在对称的正定矩阵P,Q和实数矩阵K,L满足

(16)

在如图2 所示的标准反馈系统中，B=C=I,D=0，得

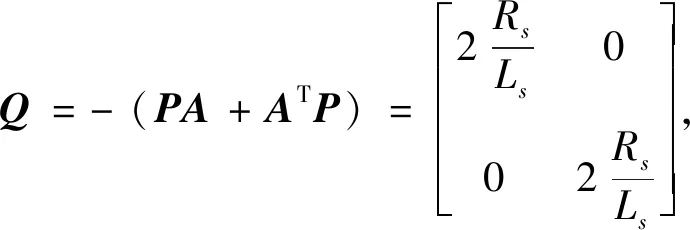
(17)

故对称正定矩阵Q存在，即线性时不变前馈系统的传递函数矩阵G(s)=(sI-A)-1为严格正实矩阵.

∀t1≥0.

(18)

按模型参考自适应系统的PI控制策略得到自适应律为

(19)

η1(0,t1)+η2(0,t1).

(20)

η1(0,t1)=

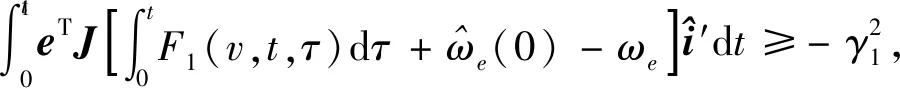
(21)

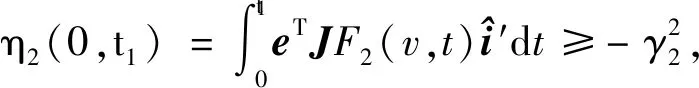
(22)

对于不等式(21)构造函数f(t)满足

(23)

式中:k>0，将式(23)代入式(21)得

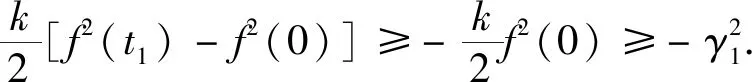
(24)

对式(23)第2个等式两边求导，并结合第1 个等式得

(25)

若不等式(22)左边的被积函数为正，则该不等式一定成立，因此取

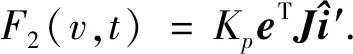
(26)

将式(26)代入式(22)得

(27)

将式(25)、式(26)代入式(19)得到

(28)

将式(7)代入式(28)得

(29)

从以上公式可以看出，转子速度的估计只受参考模型和可调模型中的电流变量影响，并且可以通过PI控制器整定得到.

(30)

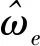
(31)

3 仿真分析

为验证基于MRAS提出的PMSM无传感器矢量控制策略的有效性和准确性，本文结合如图3 的控制框图，在MATLAB/Simulink环境中建模仿真，系统由电机模块、逆变器模块、矢量变换模块、PI模块、SVPWM模块等组成.仿真中采用的永磁同步电机参数为极对数pn=4，定子电阻Rs=2.875 Ω，定子电感Ls= 8.5 mH，磁链ψf=0.175 Wb，转动惯量J=4.8×10-5kg·m2，阻尼系数B=0.

图3 基于MRAS的三相PMSM无传感器矢量控制框图Fig.3 MRAS-based three-phase PMSM sensorless vector control block diagram

如图4～图6 所示，在电机启动阶段，MRAS算法可以很好地估计电机转速，系统在0.05 s内迅速收敛于给定转速，转速估计误差最高为20 r/min，转子位置估计误差最高为0.06 rad，系统动态性能良好.在0.5 s将给定速度由300 r/min 变为600 r/min，由图4～图6 可以看出，估计转速可以在0.05 s内快速跟踪实际转速，转速估计误差最高为25 r/min，转子位置估计误差最高为0.05 rad，估算精度基本满足矢量控制系统的要求.MRAS算法在电启动阶段和转速突变阶段的估算误差较大，但误差很快得到收敛，控制算法具有较强的鲁棒性.

如图7 所示，当电机稳定运行在转速600 r/min时，负载转矩在0.3 s由0突变为5 N·m，电磁转矩在0.02 s迅速收敛为负载转矩,电机输出电磁转矩在短时间内存在微小的估计误差，未对控制效果造成明显影响.

简化MRAS算法相比于传统MRAS算法减小了计算量，对比如图7(a)的传统MRAS算法，本文提出的如图7(b)的简化MRAS算法估算得到的转速估计曲线更平滑，稳态时转速估计误差较小，但在转速突变和转矩突变的情况下，简化MRAS的转子位置估计误差比传统MRAS算法的转子位置估计误差大，系统抗扰能力较弱，但估算精度仍然较高，可以取得较为理想的控制效果.

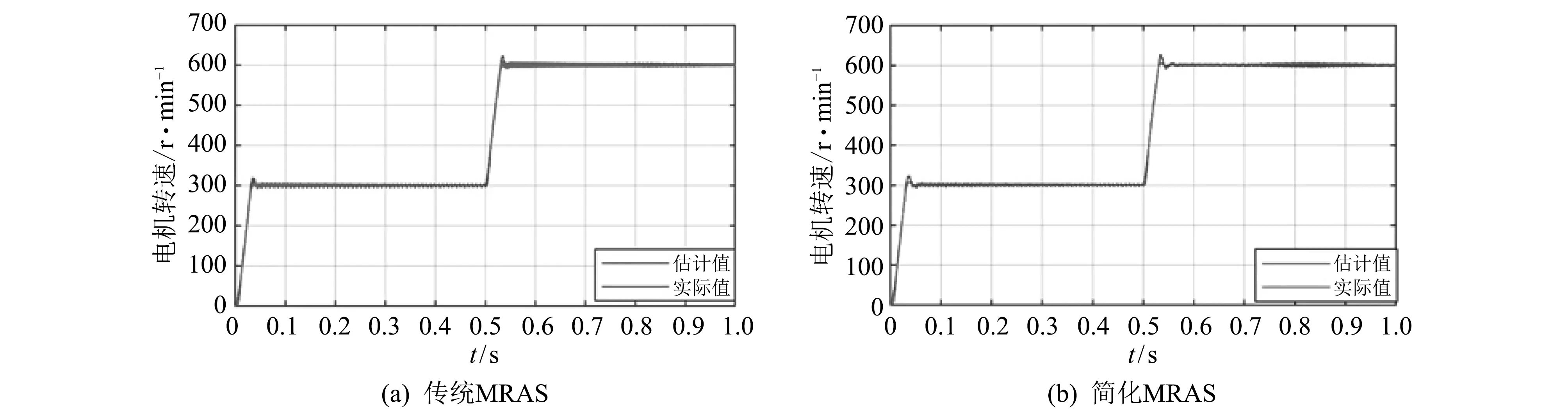
图4 转速突变时估计转速与实际转速对比Fig.4 Comparison between estimated speed and actual speed when speed changes

图5 转速突变时电机转子位置估计误差Fig.5 Motor rotor position estimation error when speed changes

图6 转速突变时电机转速估计误差Fig.6 Motor speed estimation error when speed changes

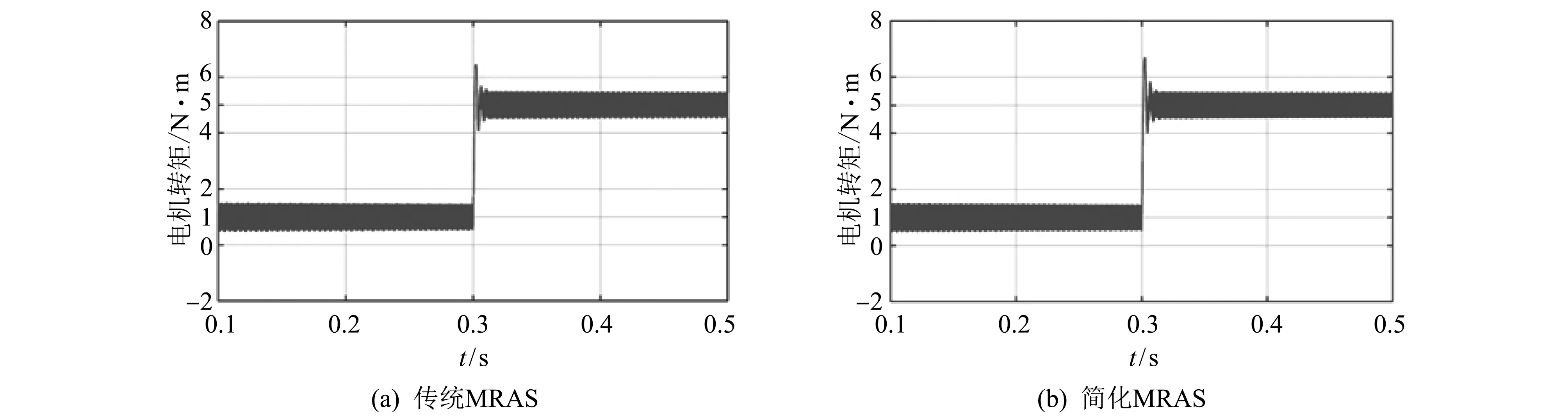
图7 负载突变时电机输出电磁转矩Fig.7 Motor output torque when load torque changes

4 结 论

本文以PMSM矢量控制技术为基础，采用模型参考自适应算法，提出了一种永磁同步电机的转速与转子位置估计的简化算法，并通过MATLAB/Simulink软件进行了仿真分析.

仿真结果表明，基于简化MRAS的转速与转子位置估算方法对于永磁同步电机的启动、转速突变以及负载转矩突变有良好的适应性，转速、转子位置估计精度高，电机控制系统的动态性能良好、鲁棒性强，能够满足许多无位置传感器控制的场合.