等温吸附量方程常数的物理含义及无因次吸附量方程

陈元千，刘浩洋，汤晨阳，干 磊

（中国石油勘探开发研究院，北京100083）

LANGMUIR（兰格苗尔）于1918年发表了著名的兰氏等温累积吸附量方程［1］，受到世人的重视和广泛应用。但应当指出，兰氏方程是一个具有两个常数的非线性经验方程。兰氏曾指出，方程的常数a和b是两个与气体物理性质和温度有关的常数。但他并不清楚a和b的实际物理含义。陈元千等于2018年发表了等温吸附量方程和解吸量方程的推导结果［2］。同时，对兰氏方程进行了完整的理论推导，得到了兰氏的等温瞬压吸附量方程和瞬压解吸量方程。陈氏方程和兰氏方程都具有两个方程常数，通过推导，明确了方程常数的物理含义，并建立了具有广泛理论意义的无因次吸附方程。陈氏方程的常数A和兰氏方程的常数a都表示样品的极限累积吸附量；陈氏方程的常数B和兰氏方程的常数b都表示等温瞬压吸附量递减率；陈氏方程的AB和兰氏方程的ab都表示样品的最大初始理论吸附量。

1 等温吸附量方程常数的物理含义

当以表压表示压力时，陈元千等提出的等温累积吸附量方程和等温瞬压吸附量方程［2］分别为：

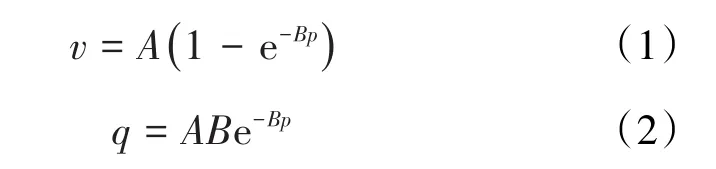
当p→∞时，由（1）式得陈氏方程的等温极限累积吸附量为：

由（3）式看出，等温极限累积吸附量等于常数A。由文献［2］知，（1）式和（2）式中的B为等温瞬压吸附量递减率。

将（3）式代入（1）式得：

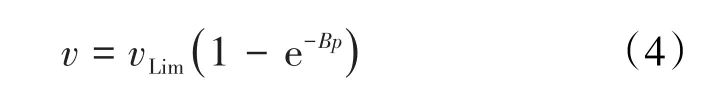
由（4）式对压力求导得陈氏的等温瞬压吸附量方程为：

当p=0时，由（5）式得p=0时的最大初始理论吸附量为：

再将（3）式代入（6）式，得陈氏的最大初始理论吸附量为：

由（7）式看出，陈氏等温累积吸附量方程中常数A与B的乘积为陈氏最大初始理论吸附量。

兰氏等温累积吸附量和等温瞬压吸附量方程［1-2］分别为：

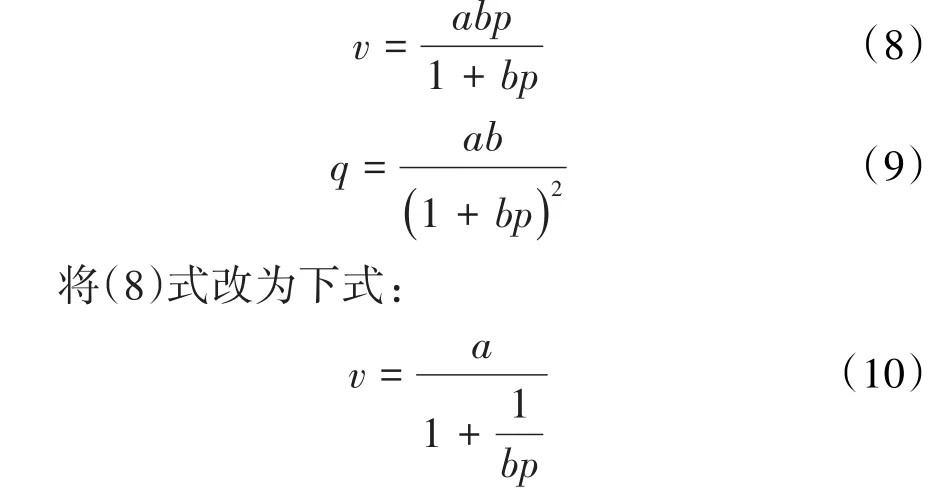
当p→∞时，由（10）式得兰氏的等温极限累积吸附量为：

由（11）式看出，兰氏的等温极限累积吸附量等于a。结合（8）式、（9）式和（10）式可知，b为等温瞬压吸附量递减率。

当p=0时，由（9）式得兰氏的最大初始理论吸附量为：

由（12）式看出，兰氏等温累积吸附量方程中常数a与b的乘积，等于p=0时的兰氏最大初始理论吸附量。

2 无因次等温吸附量方程的建立及应用

无因次等温吸附量方程是分析和评价样品对甲烷气吸附特点的重要表示方式。采用无因次吸附量方程，可以避免自然因素和人为因素对吸附分析的影响。笔者对吸附量方程2个常数物理含义的理解，为建立无因次吸附量方程提供了条件。

2.1 无因次等温吸附量方程的建立

为了建立无因次等温吸附量方程，需设定无因次等温累积吸附量和无因次吸附量2个无因次量，其表达式分别为：

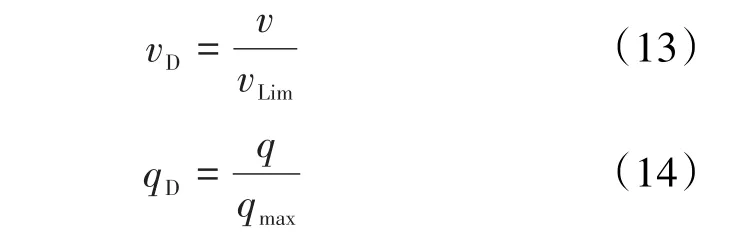
基于（13）式和（14）式的无因次量可以分别得到陈氏和兰氏的无因次吸附压力为：

将（1）式、（3）式和（15）式代入（13）式，得陈氏的无因次等温累积吸附量方程为：

再将（2）式、（7）式和（15）式代入（14）式，得陈氏的无因次等温瞬压吸附量方程为：

将（18）式代入（17）式，得陈氏的无因次等温累积吸附量与无因次等温瞬压吸附量的关系式为：

将（8）式、（11）式和（16）式代入（13）式，得兰氏的无因次等温累积吸附量与无因次吸附压力的关系式为：

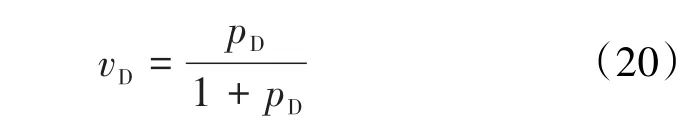
再将（9）式、（12）式和（16）式代入（14）式，得兰氏的无因次等温瞬压吸附量与无因次吸附压力的关系式为：

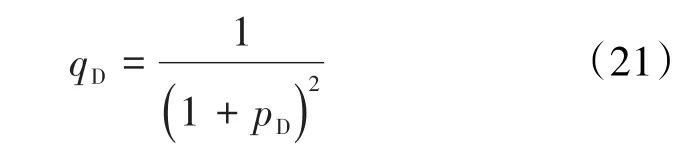
给定不同的pD值，由（17）式和（18）式，以及由（20）式和（21）式计算得到的陈氏和兰氏的无因次等温吸附量数据绘于图1。由图1可以看出，陈氏曲线与兰氏曲线存在一定的差异。这是两种方程建立的基础不同所致。陈氏方程是经过理论推导得到的方程，而兰氏方程则为经验方程。

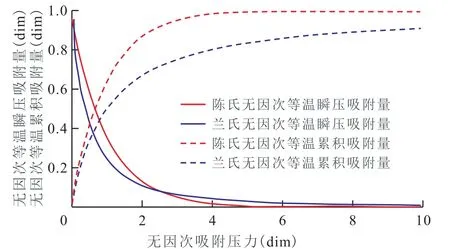
图1 陈氏和兰氏的无因次等温吸附量曲线Fig.1 Dimensionless adsorption isotherm curves of Chen's and Langmuir equations

2.2 无因次等温吸附量方程的应用

若设pS为等温饱和吸附压力，那么，由（15）式和（16）式可得陈氏和兰氏的无因次等温饱和吸附压力分别为：

由（17）式和（20）式可得陈氏和兰氏的无因次等温饱和累积吸附量分别为：

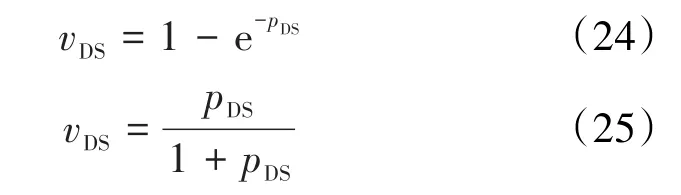
陈氏和兰氏的等温饱和累积吸附量与无因次饱和吸附压力的关系式分别为：

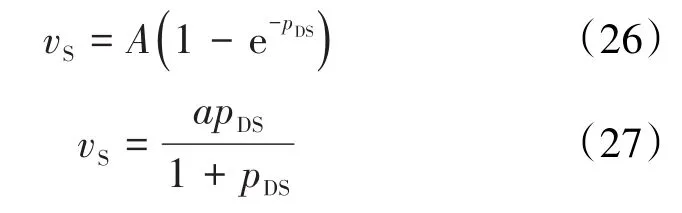
3 应用举例

3.1 实例的原始基础资料

对MAVOR等提供的美国3个产煤盆地的3个地层的16个样品［3］进行注入甲烷气的等温吸附实验，其地质基础资料如表1所示。

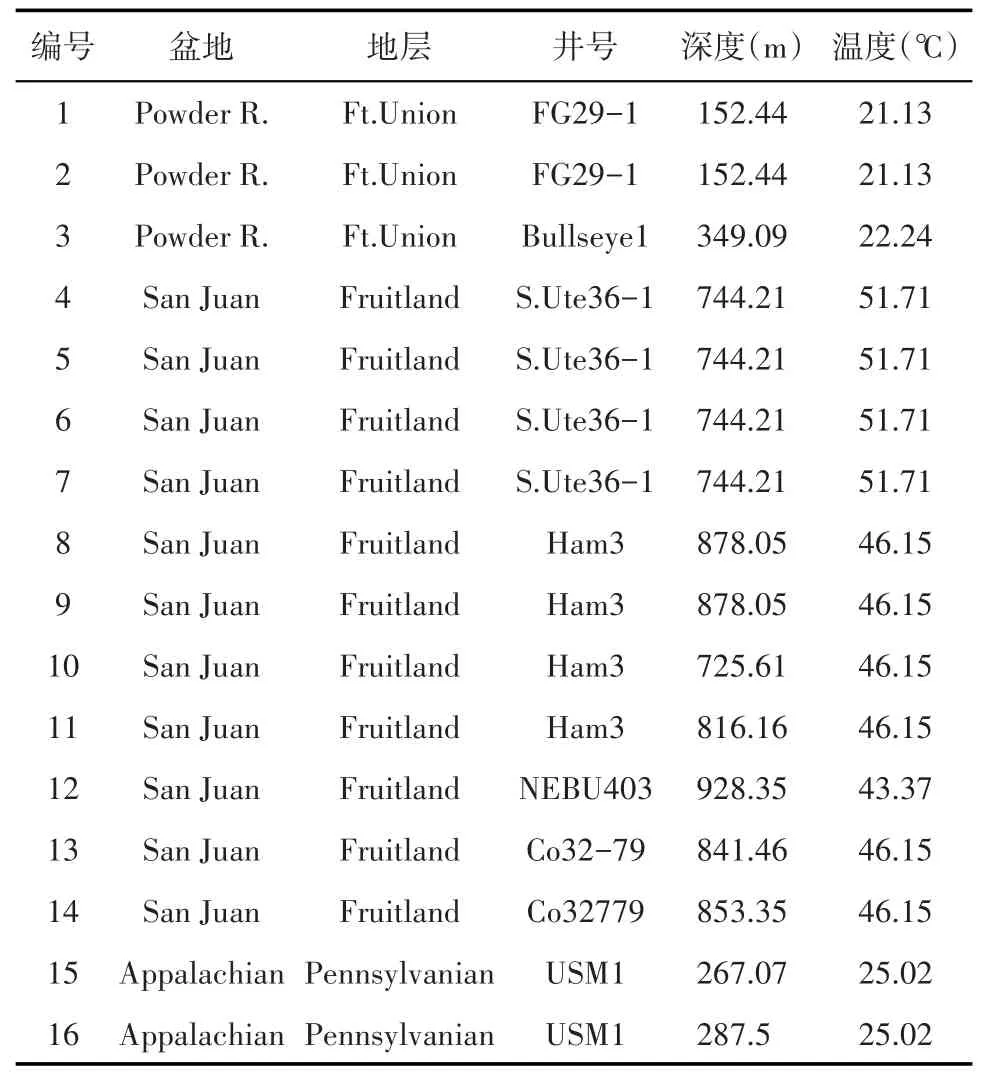
表1 16个样品的地质基础资料Table1 Basic geological data of 16 samples

由16个样品等温吸附实验取得的吸附压力和累积吸附量（表2）可以看出：在吸附实验开始时，最低和最高的吸附压力分别为0.10和1.28 MPa；最低和最高累积吸附量分别为0.33和8.65 m3/t。在吸附实验结束时，最低和最高的吸附压力分别为2.75和14.30 MPa；最低和最高的累积吸附量分别为2.00和36.69 m3/t。利用表2中的吸附量数据，绘制等温累积吸附量曲线。由图2可以看出，样品的等温累积吸附量曲线符合陈氏和兰氏方程描述的特征。

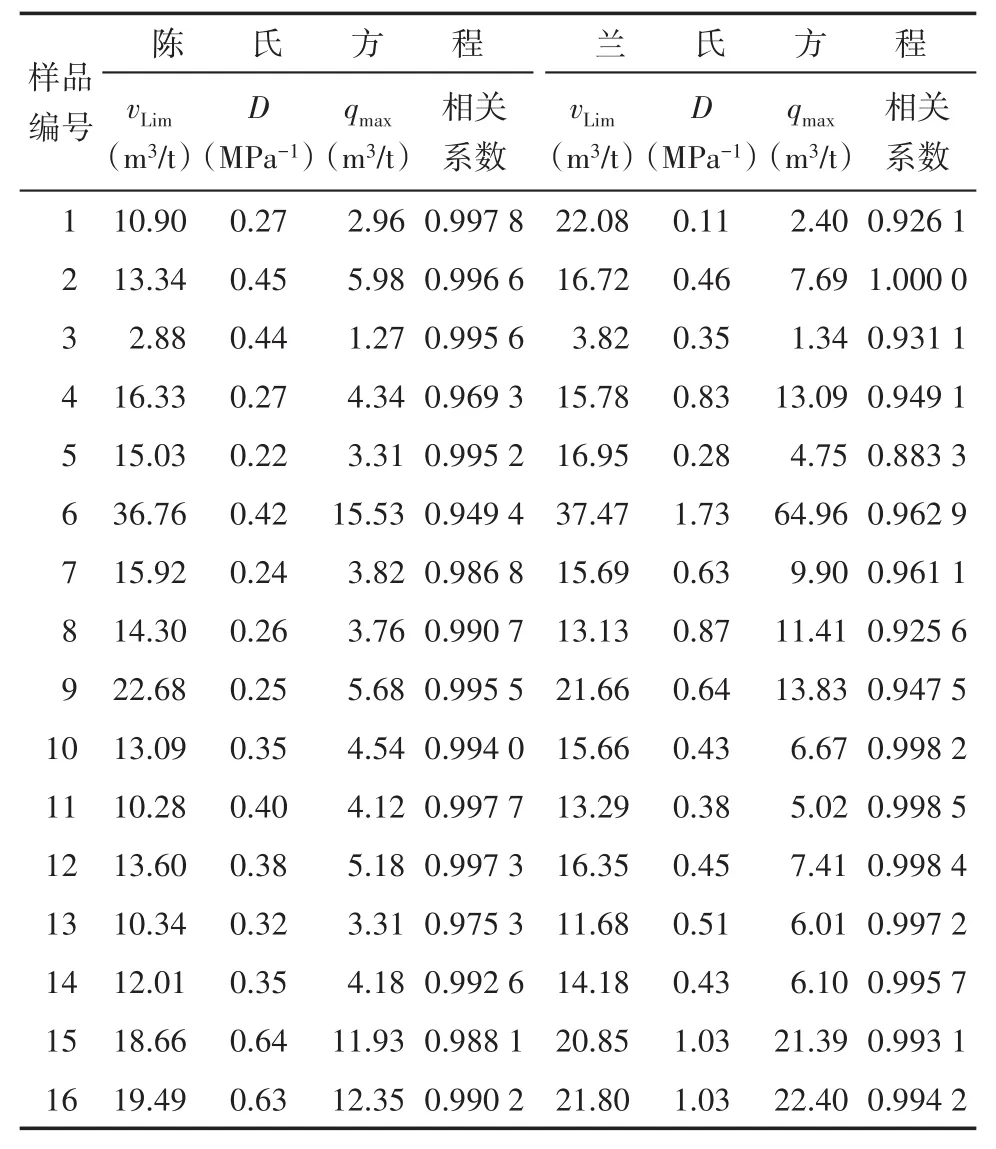
表3 16个样品吸附实验评价结果Table3 Experimental evaluation results of 16 samples

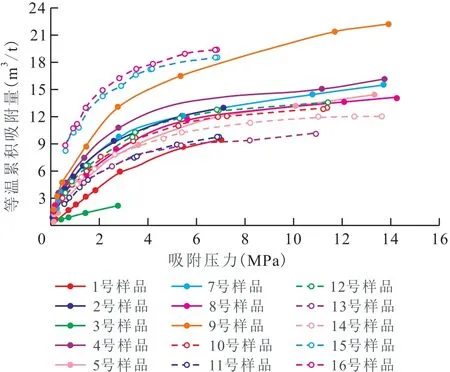
图2 15个样品的等温累积吸附量曲线Fig.2 Cumulative adsorption isotherm curves of 15 samples

3.2 16个样品的评价结果

利用陈氏和兰氏方程对16个样品进行评价，得到的等温极限累积吸附量（vLim）、等温瞬压吸附量递减率（D）（其值等于B）和最大初始理论吸附量（qmax）如表3所示，并将数据分别绘于图3至图5上。结果表明：陈氏和兰氏的等温极限累积吸附量基本一致（图3）；而陈氏与兰氏的等温瞬压吸附量递减率和最大初始理论吸附量评价结果差异明显（图4，图5），陈氏的评价结果比较稳定，而兰氏评价结果变化非常明显，个别的D值甚至大于1.0。

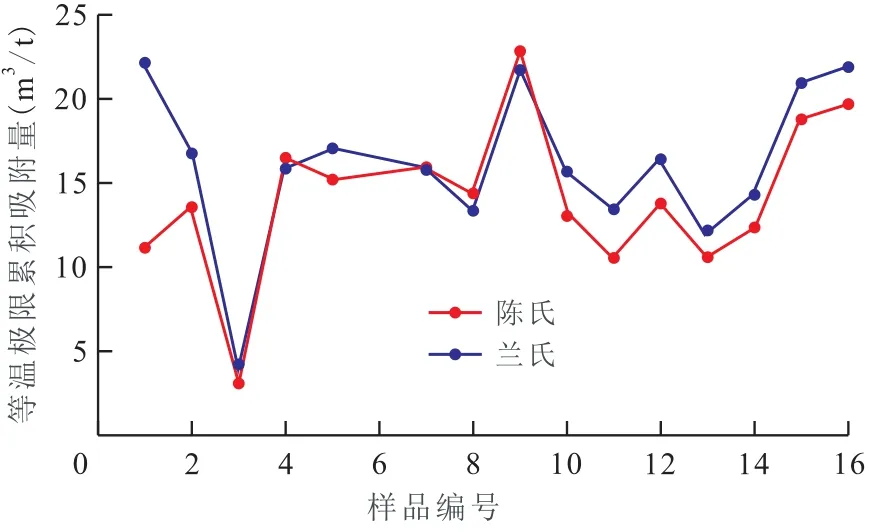
图3 15个样品的等温极限累积吸附量对比Fig.3 Comparison of the limit of cumulative adsorption capacity of 15 samples

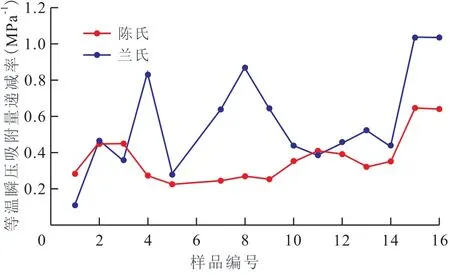
图4 15个样品的等温瞬压吸附量递减率对比Fig.4 Comparison of D values of 15 samples

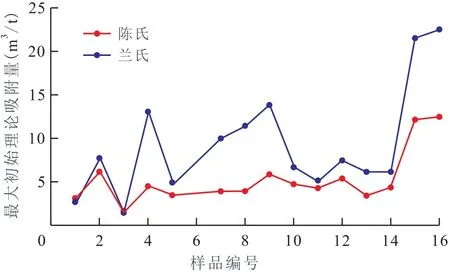
图5 15个样品的最大初始理论吸附量对比Fig.5 Comparison of qmaxof 15 samples

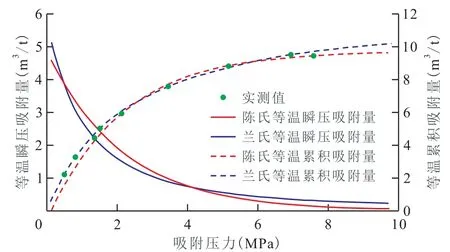
图6 陈氏和兰氏方程的预测曲线对比Fig.6 Comparison of the predictions of CHEN's and Langmuir equation

3.3 陈氏和兰氏方程预测结果的对比

根据表2中11号样品的数据，分别利用陈氏和兰氏方程计算的等温瞬压吸附量和等温累积吸附量绘于图6。由图6可以看出，陈氏与兰氏方程预测的结果具有很好的一致性。因此，两者可以起到互相验证的作用。

3.4 等温饱和吸附量的确定

正如前述，等温饱和吸附量是评价页岩吸附气和煤层吸附气资源量的重要参数。因此，如何确定等温饱和吸附量是一项重要的工作。假定页岩气和煤层气的等温饱和吸附压力等于岩层的静水柱压力为：

由表1可以查到11号样品的埋深为816.16 m。将此值代入（29）式得等温饱和吸附压力为：

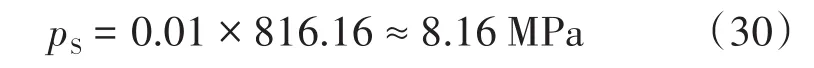
再将pS值和文献［2］中求得的兰氏方程中的a=12.61和b=0.446 4代入（8）式，得兰氏的等温饱和累积吸附量为：

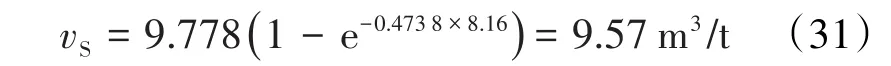
再将pS值和文献［2］中求得陈氏方程中的A=9.778和B=0.473 8代入（1）式，得陈氏的等温饱和累积吸附量为：

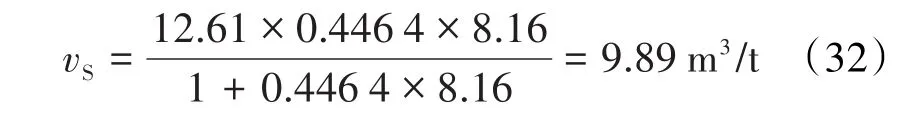
将B和pS值代入（22）式，得陈氏的无因次等温饱和吸附压力为：

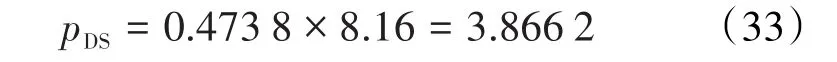
再将pDS和A值代入（26）式，得陈氏的等温饱和累积吸附量为：

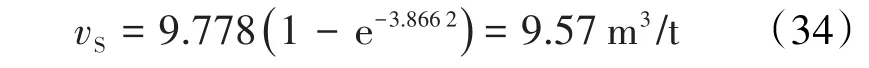
将b和pS值代入（23）式，得兰氏的无因次等温饱和吸附压力为：

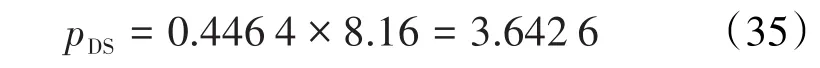
再将pDS和a值代入（27）式，得兰氏的等温饱和累积吸附量为：

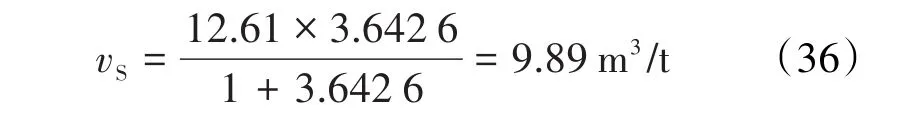
上述计算结果表明，无论是解析式或是无因次法，陈氏方程和兰氏方程预测的等温累积吸附量基本相同。

4 结论

基于文献［2］的研究成果，经过理论推导得到陈氏和兰氏方程2个常数的物理含义，建立了无因次等温吸附量方程；提出了确定饱和吸附压力和饱和吸附量的方法。这为页岩气和煤层气吸附量资源的评价提供了重要参数。方程的应用结果表明，陈氏等温吸附量方程与兰氏等温吸附量方程具有很好的一致性。然而，兰氏的等温累积吸附量方程是一个经验方程，在理论上不如陈氏方程可靠完善。

符号解释

v——1克岩样等温累积吸附量，m3/t；A，B——陈氏等温吸附量方程常数；p——吸附压力，MPa；q——1克岩样等温瞬压吸附量，m3/t；vLim——1克岩样等温极限累积吸附量，m3/t；a，b——兰氏等温吸附量方程常数；vD——1克岩样无因次等温累积吸附量，dim；qD——1克岩样无因次等温瞬压吸附量，dim；pD——无因次吸附压力，dim；pS——等温饱和吸附压力，MPa；pDS——无因次等温饱和吸附压力，dim；vDS——无因次等温饱和累积吸附量，dim；vS——1克岩样等温饱和累积吸附量，m3/t；D——等温瞬压吸附量递减率，MPa-1；ρw——水的密度，g/cm3；H——岩样的地层埋深，m。