四轴飞行器的欧拉动力学方程

刘彦超

（包头轻工职业技术学院，包头 014030）

随着小型无人机在航拍、测绘勘查、电力巡线、灾难救援以及突发事件应急处理等领域的应用越来越广泛，小型无人机的研究已逐渐成为一个热点领域。

图1 四轴飞行器结构简图

四轴飞行器有十字型和X型两种，其中十字形结构如图1所示，四个电机和螺旋桨分别对称分布在机体的前、后、左、右支架末端，且处于同一高度，电机型号和螺旋桨的尺寸均相同，其中1号和3号电机逆时针旋转，2号和4号电机顺时针旋转（规定1#电机所指方向为x轴正方向，2#电机所指方向为y轴正方向）。当四个旋翼的角速度ω1、ω2、ω3、ω4相等时，（理想状态下）其对应的升力F1、F2、F3、F4也相等，进而在升力与重力的共同作用下，机体可悬停或起降；当ω1≠ω3时，F1和F3的差分变化产生俯仰力矩Ty，使得αy角变化；当ω2≠ω4时，F2和F4的差分变化产生滚转力矩Tx，使得αx角变化；当 ω1+ω3≠ω2+ω4时，四个旋翼的反扭合力矩Tz使得机体发生偏航，αz角变化。注意这里的αx、αy及αz不是欧拉角，而是机体适时偏转角度。

显然，机体姿态角的变化不仅仅与力矩Tx、Ty及Tz有关，还和机体的转动惯量有关，所以可用欧拉动力学方程来描述机体所受合力矩：

欧拉动力学方程用于描述刚体绕定点运动，是研究多旋翼无人机的有利工具，但多数力学教材及惯性导航文章对其物理意义的讨论都比较少，只是由哥氏定理（向量绝对导数与相对导数的关系式）直接得出结论，所以多数人对其物理意义并不是很清楚。本文利用陀螺力矩概念对欧拉动力学方程进行了推导和论证，可供同行参考。[1]

一、陀螺力矩

图2 陀螺力矩

如图2所示，质量为m的刚体绕z轴以角速度ω→高速旋转，形成动量矩G→。平行于x轴的力F→作用于刚体的质心位置r→，将产生一个指向y轴正方向的力矩：

显然力矩T→作用Δt时间后，将产生一个指向y轴方向的动量矩增量：

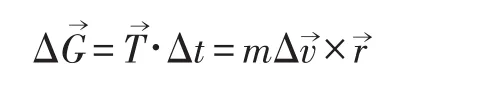
这时刚体的总动量矩为：

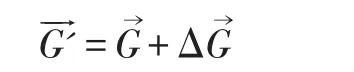
综上所述，陀螺力矩可定义为是陀螺力图保持自身转轴方向不变，所产生的用于抵抗外力矩T→的力矩。[2]

二、刚体动力学方程

如图3所示，这里的ω→可看成是以坐标轴为转轴的三个角速度向量及的合成，显然刚体在 x、y及 z方向上的动量矩分别为：当转距 T→作用于刚体时，刚体将加速旋转。同样转矩也可沿坐标轴分解为三个向量，即及

图3 z轴方向的动量矩增量

显然刚体以角速度ω→y绕y轴旋转Δt时间后，x方向的转轴会上翘个弧度，从而动量矩会向上偏转变为。所以存在动量矩增量，其方向为z轴的正向。当 Δt足够小时，可以将由及组成的三角形看作是一个扇形，显然有：

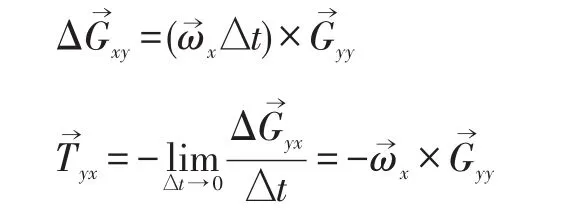
综上所述，显然有

同理可得：

显然：

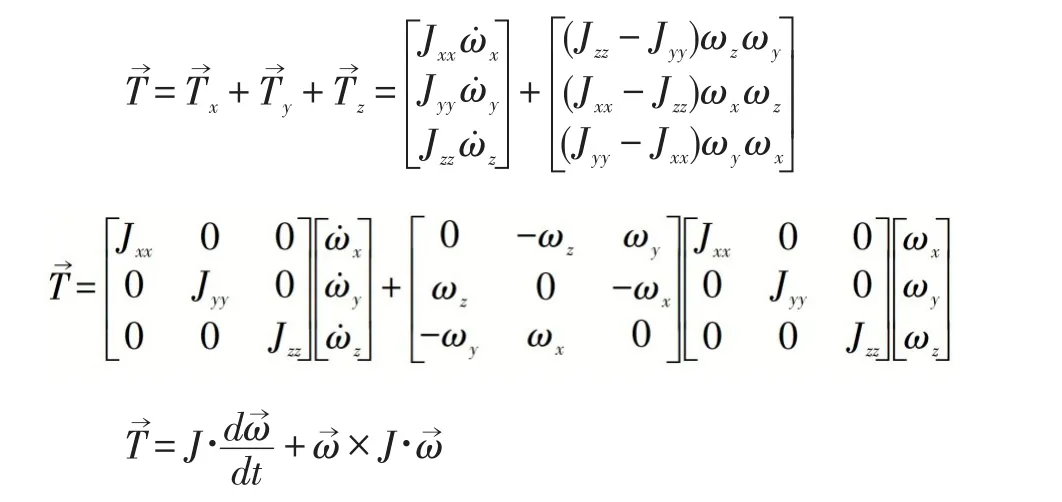
三、结论与效果

通过本文对欧拉动力学方程的推导来看，合外力矩 T→ 可分为两部分，一部分是 J(dω→ dt)，它用于产生机体角加速度，另一部分是 ω→×J∙ω→，它用于抵抗陀螺力矩。

本文利用陀螺力矩概念对欧拉动力学方程进行了推证，其物理意义更加明确，这将会增进无人机爱好者对四轴飞行器动力学机理的理解，推进无人机事业的发展。[4]