机器学习在汽车销量预测中的应用

王书鹏 迮恒鹏 王 涛 黄素珍 刘桂兰

（1.盐城工学院经管学院；2.盐城工学院电气学院；3.盐城工学院数理学院）

针对汽车销量预测研究问题，目前大多数建立的是传统的时间序列分析模型[1-7]。它们存在两点不足：（1）仅利用汽车历史销售数据解决汽车销量预测问题，事实上存在众多销量影响汽车销量预测的因素，比如原材料因素、消费者因素、网络传播因素、宏观经济因素等；（2）需要事先假定历史销量和销量之间呈线性关系，事实上销量和历史销量以及其他影响因素之间存在高度非线性的关系。本文将利用机器学习技术[8]，建立多因素非线性自回归汽车销量预测模型。

一、销量预测模型的构建

选取本月汽车销量作为因变量，解释变量包括历史汽车销量、钢材产量、橡胶轮胎产量、货币供应量、百度搜索指数、居民消费价格指数等，为了方便表述，文中采用表1中的符号建立销量预测模型。

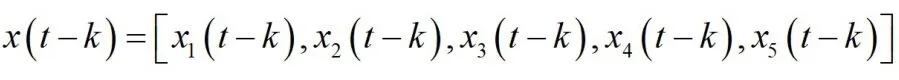
为前k月因素矩阵。

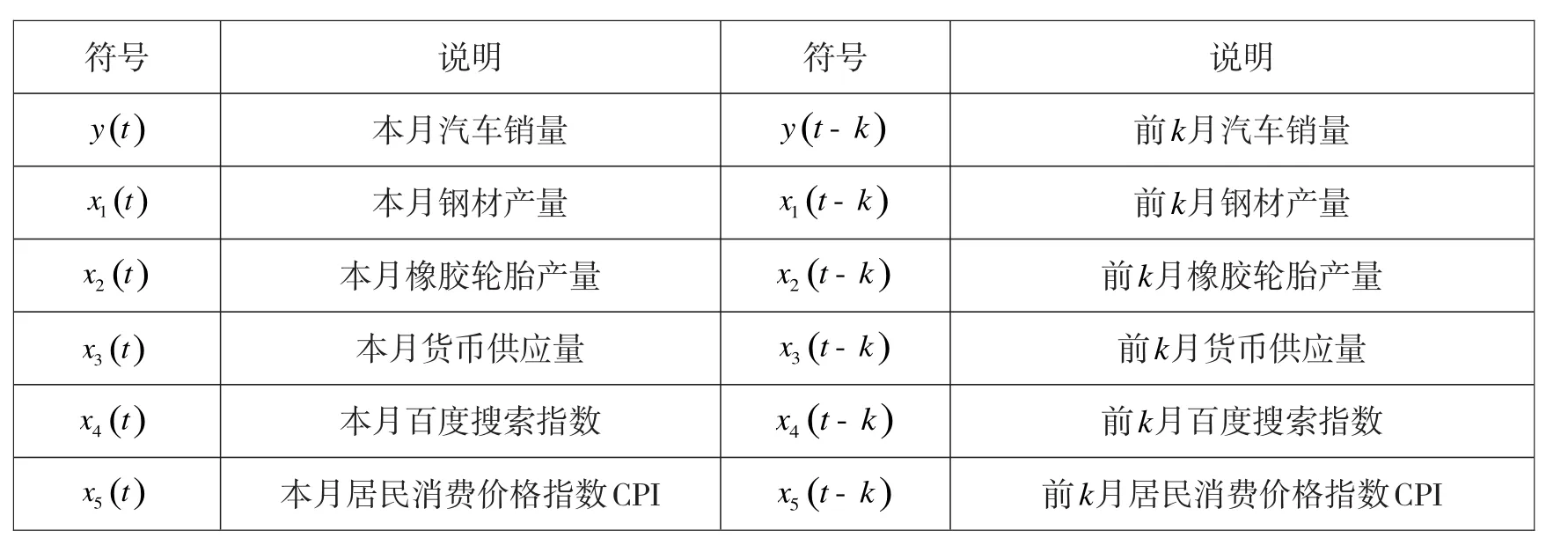
表1 符号说明

（一）无因素非线性自回归模型

如果仅仅考虑历史销量数据对销量的影响，则得到无因素非线性自回归模型为

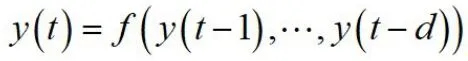
（二）多因素非线性自回归模型

假设销量不仅与历史销量有关，还与钢材产量、橡胶轮胎产量、货币供应量、百度搜索指数、居民消费价格指数等有关，则得到多因素非线性自回归模型为

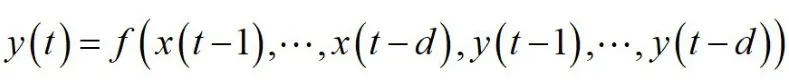
二、仿真分析

利用机器学习技术，以大众品牌汽车为例建立销量预测的多因素非线性自回归模型。

（一）数据的获取与处理

采用2011年1月至2018年12月共96个月的数据。

大众品牌汽车月销量数据，来源于车主之家网站https://www.16888.com。

钢材产量、橡胶轮胎产量、货币供应量、居民消费价格指数的月度数据，来源于国家统计局网站http://www.stats.gov.cn/。

百度搜索指数月度数据，来源于百度指数网站http://index.baidu.com。

为了消除数据量纲的影响，将上述数据作归一化处理：

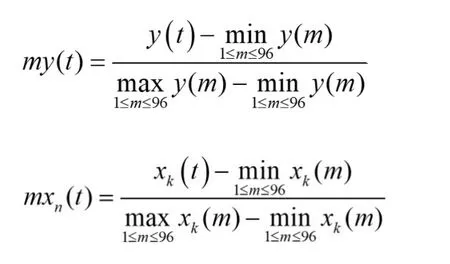
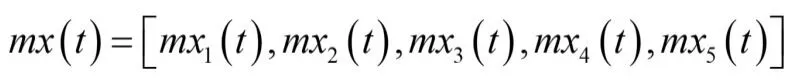
（二）模型参数的设定

非线性自回归的神经网络主要有输入层、隐含层和输出层、输入输出延时层构成。选取隐含层为25，延迟数d为12，其基本结构如图1。

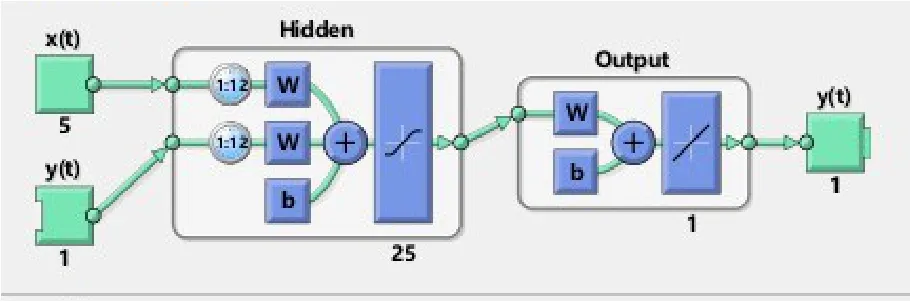
图1 非线性自回归神经网络的基本结构

（三）训练数据、验证数据和测试数据的划分

将96个样本数据划分如下：训练数据占70%，验证数据占15%，测试数据占15%。

（四）网络训练

选择训练算法Levenberg-Marquardt，该算法要求样本容量足够大，但是记忆速度快，当验证数据均方误差不再增长，训练自动停止。

（五）预测结果分析

本文建立的大众品牌销量预测模型的结果如表2。

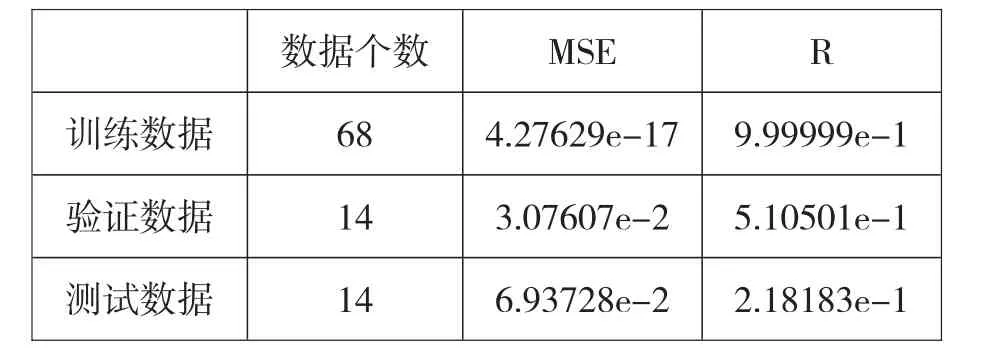
表2 大众品牌销量预测模型的结果

表2中MSE为预测销量和实际销量之间的均方误差，MSE越小预测效果越好，当MSE=0时，预测销量=实际销量。R为预测销量和实际销量的相关系数，当R=1时，则预测销量和实际销量完全相关，当R=0时，则预测销量和实际销量完全不相关。该模型测试数据MSE=0.0694，小于0.1，但R=0.2182，小于0.5，预测效果一般。这是因为样本数据量偏少，只有增加样本容量，才能提高机器学习预测的精度。