基于混合系统建模预测控制的列车自动驾驶优化运行

汤旻安，王攀琦

基于混合系统建模预测控制的列车自动驾驶优化运行

汤旻安1, 2，王攀琦1

(1. 兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070；2. 兰州理工大学 机电工程学院，甘肃 兰州 730050)

针对现有列车自动驾驶速度追踪精度不高的问题，提出一种基于混合系统神经网络反馈补偿控制的模型预测控制算法。根据混合系统建模的特点与优势，引入辅助变量，建立混合系统列车运行动力学模型。为了便于求解包含约束的预测控制律，采用二次规划方法求出满足列车各项性能指标的控制作用序列。神经网络反馈控制器用于对系统目标速度与实际速度之间的误差进行在线学习并求出一个补偿控制量，并将补偿后的控制力作用于列车系统模型。研究结果表明：该控制结构包含补偿控制策略，可以较大程度减小系统跟踪误差，保留模型预测控制的优势，同时提高系统的控制精度。

混合系统；神经网络；模型预测控制；自动驾驶；优化运行

近年来，针对列车自动驾驶的研究越来越广泛，通过使列车跟随既定的目标曲线，取代了司机的工作，同时提高了运行效率。因此，设计能够进行精确跟踪并保证舒适度、安全性各指标的控制器对铁路运营有重要意义。在列车自动驾驶问题上，有多种建模的方式，同时有多种控制算法被应用于列车运行控制，如PID控制、模糊控制和两级神经网络控制等。Ganesan等[1]通过对列车车辆、列车编队、滚动阻力、轨道环境等方面的研究，提出了一种高速列车的非线性纵向动力学模型，并对列车自动运行的纵向控制器设计进行了研究。董海荣等[2]利用模糊PID软切换控制算法及模糊规则完成模糊控制与PID之间的切换，实现了ATO系统调速控制的平滑过渡。Gionata等[3]讨论了跟踪算法的设计，介绍了一种基于模型预测控制(MPC)的ATO系统，用于跟踪电动有轨电车位置路径，突出了模型预测控制在处理多输入输出约束、可测量干扰等方面的优势。在过去的几十年中，已经在世界范围内进行了大量关于人工神经网络在解决工程问题中的应用的研究。神经网络控制具有自学习、非线性适应性信息处理能力，可以通过在线或离线学习不断改进控制系统的性能，达到满意的控制效果。余进等[4]将两级神经网络应用在高速列车ATO系统中，对高速列车运行过程进行控制，前一网络获得列车在特定位置的最佳运行工况，后一网络据此推理出列车在当前条件下的运行速度，具有一定的可行性。董海鹰等[5]从我国高速铁路的目标－距离速度控制模式出发，设计了基于模糊神经网络的列车速度预测控制算法，具有一定的参考价值。目前为止，非线性网络结构在反馈控制中的理论和应用已有充分记录，神经网络为非线性参数化学习系统提供了自适应控制技术的扩展[6−7]。Kazuhiko 等[8−9]提出了一种自适应输出反馈控制方案，研究了使用神经网络的反馈控制器的控制性能，评估结果具有一定的可行性。混合系统本身是一种连续状态和离散状态相互作用相互耦合的一类复杂系统，系统内部连续状态和离散状态共存。列车运行过程本身是一种连续变量和离散变量相互作用影响的过程。XU等[10]提出用一个混合模型预测控制框架来设计ATO系统的控制器，用于在硬约束条件下实现速度控制，但是追踪精度还不尽理想。王龙生[11]提出基于混合系统模型预测控制HMPC的列车自动驾驶策略，在一定程度上实现了列车的准时高效运行。本文考虑首先对列车进行精确建模，针对列车运行过程动力学特性的复杂性，建立基于混合系统的列车动力学模型。基于混合系统进行建模可将列车动力学特性中的连续状态和离散状态进行整合，更准确有效地分析列车的运行状态[12−13]。本文在文献[10]的基础上，为了提高列车控制器追踪目标曲线的精度，同时在一定程度上克服扰动的影响，在预测控制的基础上，提出引入神经网络反馈控制，构成一种具有反馈补偿的预测控制策略，并进行了仿真和实验研究。

1 混合系统列车动力学模型

混合系统的建模方法在描述混合系统的行为特征方面的能力各不相同，不同的建模方法有各自的特点和便利之处。研究结果表明，混合系统的模型在一定的附加条件下都是等价的。

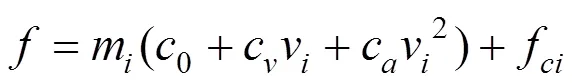
由于运行阻力的非线性，随着列车速度的增加，运行阻力也跟随速度逐渐变化，因而需要对其进行线性化处理。运行阻力分段线性化函数表示为

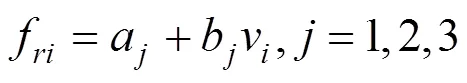
线性化处理后参数取值如表1。

表1 列车运行阻力分段参数

选取其中任意一节车厢，例如第2节车厢，其运动学方程为

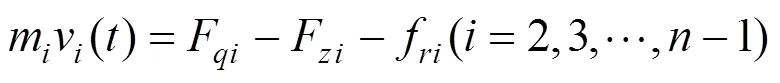
通过分段线性化的方法处理之后，对非线性列车模型式(3)进行离散化，得到状态空间方程为

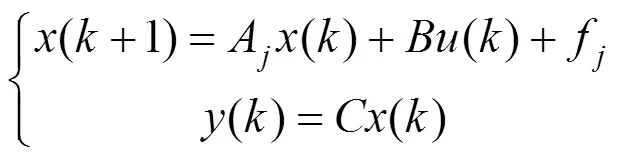
仿真过程为了简化计算，取列车车厢数为3，则有

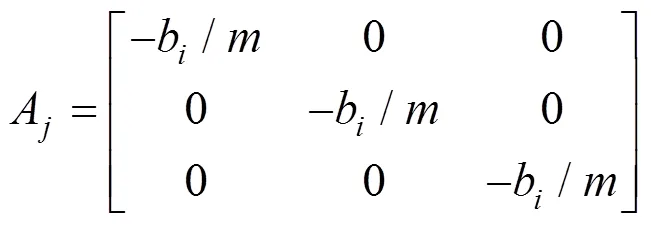
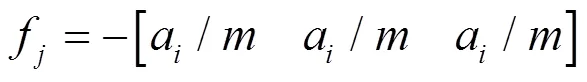
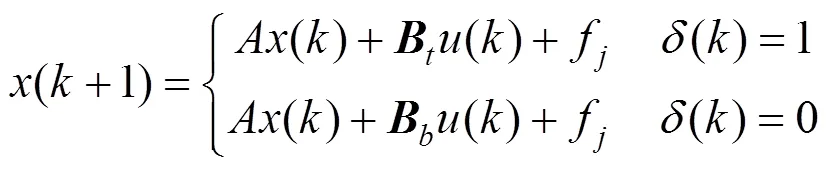
式中：和分别为牵引力矩阵和制动力矩阵。混合逻辑动态模型(MLD)具有一般性，混合系统的多个模型都可以转化为MLD模型。利用MLD模型可在一个集成的框架下方便地对混合系统进行分析和综合[14]。

对式(5)展开得到

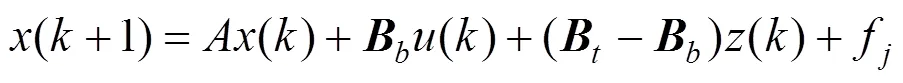
转换得到的MLD方程为

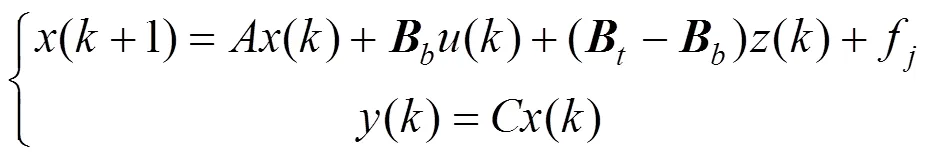
辅助变量及输入需要满足的约束为

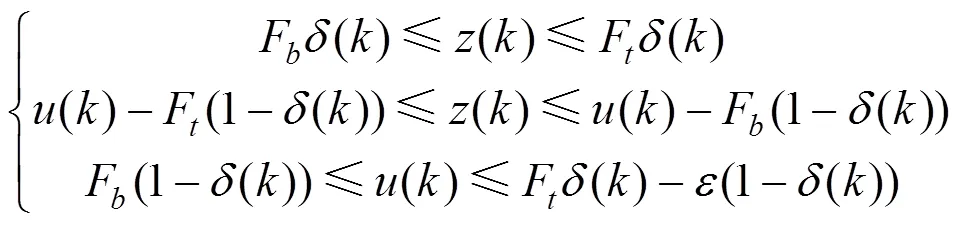
2 性能指标函数

列车在实际运行过程中，需要考虑执行器饱和特性、列车安全限速和车厢间最大耦合力等约束条件，同时还需综合考虑运营准时性、节能高效和乘客乘坐舒适度等性能指标。性能指标函数的选取是保证控制器设计目标实现的保障，同时需要满足列车自动驾驶条件的条件，通过优化指标的实现，使系统在未来的输出满足系统跟踪要求[15]。

2.1 准时性和定点停车

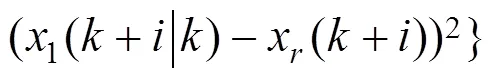
2.2 乘客乘坐舒适度

2.3 运行节能

综上所述，总的性能指标函数将由3个部分组成，根据实际情况选择合适的权重，总的优化函数为

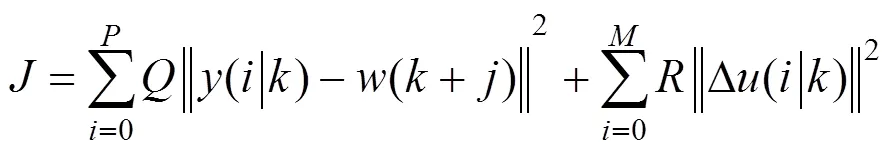
将其化简为向量形式有

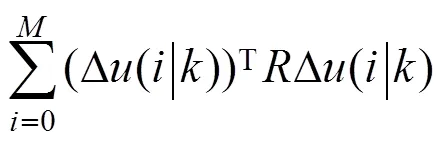
式中：为优化变量的个数，也即控制增量的维数；为预测时域的步长，既是对未来个时刻进行预测。越小，控制机动性越弱。为误差权重矩阵，为控制权矩阵。控制权重矩阵的作用是对Δ的变化加以适度的限制。它是作为一种软约束加入性能指标之中，可以防止控制量过于剧烈的变化。

在预测控制中，为了使输出()按一定响应速度平滑地过渡到设定值，参考轨迹通常取为下一阶滞后模型，有

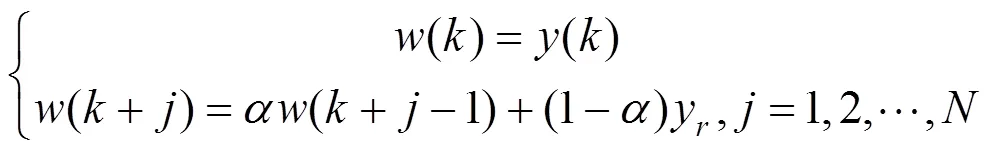
3 控制器设计

本文提出的基于模型预测控制、神经网络反馈补偿控制原理如图1所示。神经网络反馈补偿控制器在控制过程中对跟踪误差进行在线学习，并计算产生一个反馈补偿控制量，对控制过程中的系统误差进行补偿。最终得到的控制律即是由这二者组成。这种控制结构采用神经网络的学习特性，可以减小控制系统误差，使输出精确跟随既定曲线，保证系统有较好的动态性能。

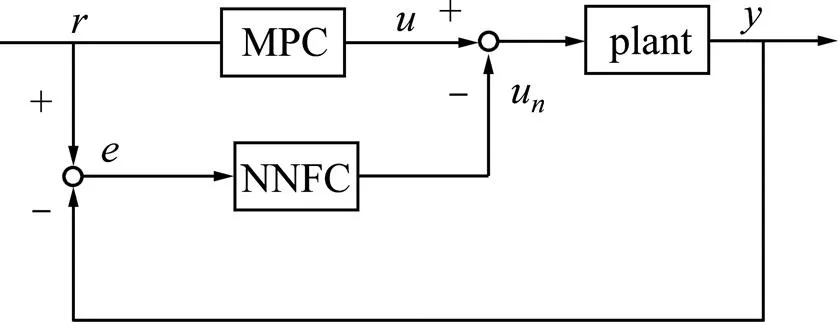
图1 神经网络反馈模型预测控制框图

3.1 模型预测控制

预测控制只注重模型的功能，通常只实施当前时刻的控制作用。采用模型预测控制来设计列车控制器，其优势在于可以充分考虑系统输入及状态约束同时处理多目标优化问题等优点。模型预测控制一般包括预测模型、滚动优化和反馈校正3个部分。令为优化变量，则

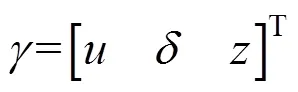
未来输出预测表示为

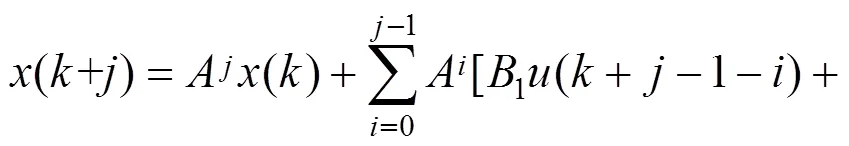
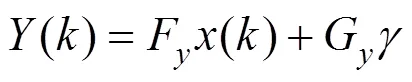
其中，

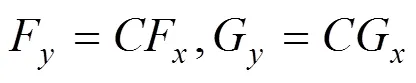
将预测输出量代入性能指标中，得到将最小化性能指标等价于函数最小化混合整数二次规划问题如下。

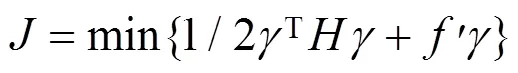
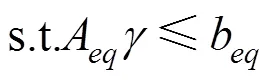
其中，

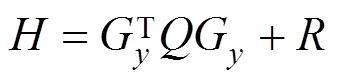
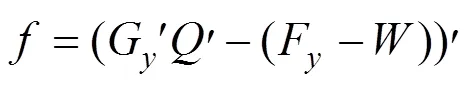
式中：为柔化后的参考轨迹曲线。由于逻辑变量及不等式约束的出现上式没有解析解，需要将其转化为标准混合整数二次规划问题进行求解[17−18]。

考虑约束条件(9)，对其转化得到

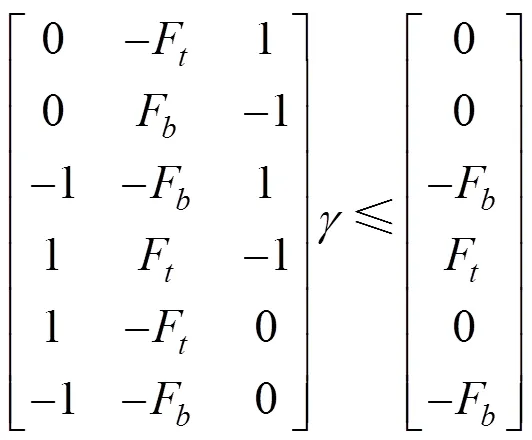
式中：F和F为每节车厢的最大牵引力和最大制动力。

选取有效集法来解决二次规划问题，通过求解等式约束的可行解，并不断加以改进，直至获得最优解。主要步骤为：

1) 假设在第次迭代中获得可行解()；

4) 判断是否获得了最优解。

3.2 神经网络反馈补偿控制

为了简化计算量，并保证实时性，采用BP单隐层神经网络对系统实时误差进行在线学习，得到误差补偿控制律。采用的权重更新规则方法即为梯度法。当它收到期望误差时，经过训练，产生一个补偿量，对模型预测控制得出的控制律进行在线补偿。对一个单输入单输出神经网络，其结构如图2所示。

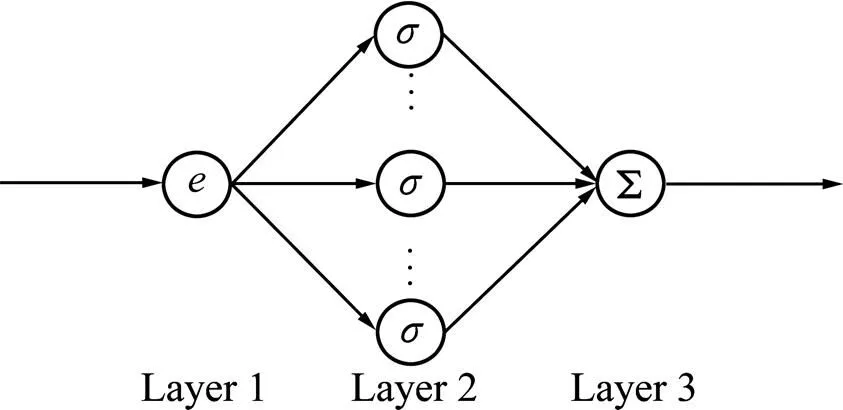
图2 神经网络结构简图

定义神经网络每一层的输入为，输出为，则每一层对应各自的计算过程。

输入层：连接系统的实时误差，并将其直接传递至下一层

隐含层：数量为1，包含5个节点，每个节点计算对激励函数下的激励值。隐含层采用Sigmoid函数作为其传递函数，输入与输出的关系为：

输出层：进行运算，计算实时补偿并输出

定义优化目标函数为：

其中：和分别为目标速度和实际速度值。神经网络学习的目标即是使目标函数最小，输入层与隐含层权向量为w，隐含层与输出层权向量为w。

输出层的误差梯度为

隐含层的误差梯度为

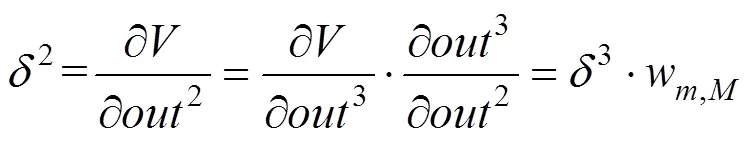
目标函数对输入层与隐含层权向量w的修正公式为

目标函数对隐含层与输出层权向量w的修正公式为

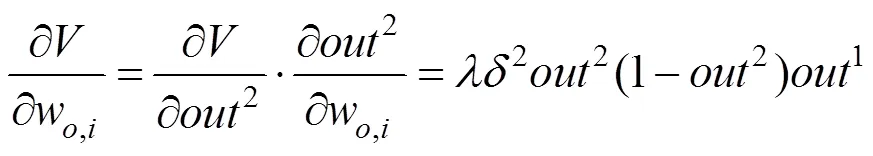
神经网络权值调整的计算方法如下：

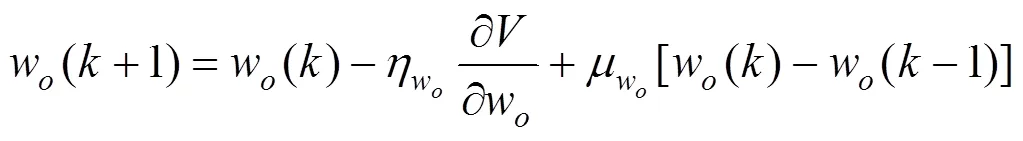
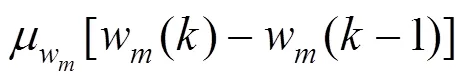
控制系统得到最终的控制量为MPC控制器、神经网络反馈控制的控制输出的代数和，用最后得到的总控制律来作用于列车模型。因此，最终的控制量为

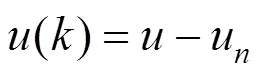
4 仿真结果分析

高速铁路列车现多为动力分散型动车组，新建线上速度一般不超过350 km/h，本文选取的CRH3型动车组参数如表2所示。控制器的参数如表3所示。速度控制器的功能实质上是保证被控列车能够准确及时地跟随列车运行过程中的目标曲线。

表2 CRH3列车参数

表3 控制器参数

为了验证神经网络补偿的有效性，这里采用神经网络补偿作用于模型预测控制，让列车跟随一条时变的线段(该曲线在1 100 s进行制动减速)，如输出图形中红色曲线所示，并与未采用神经网络补偿控制的模型预测控制器进行比较，验证过程中，保证MPC控制器控制参数相同。

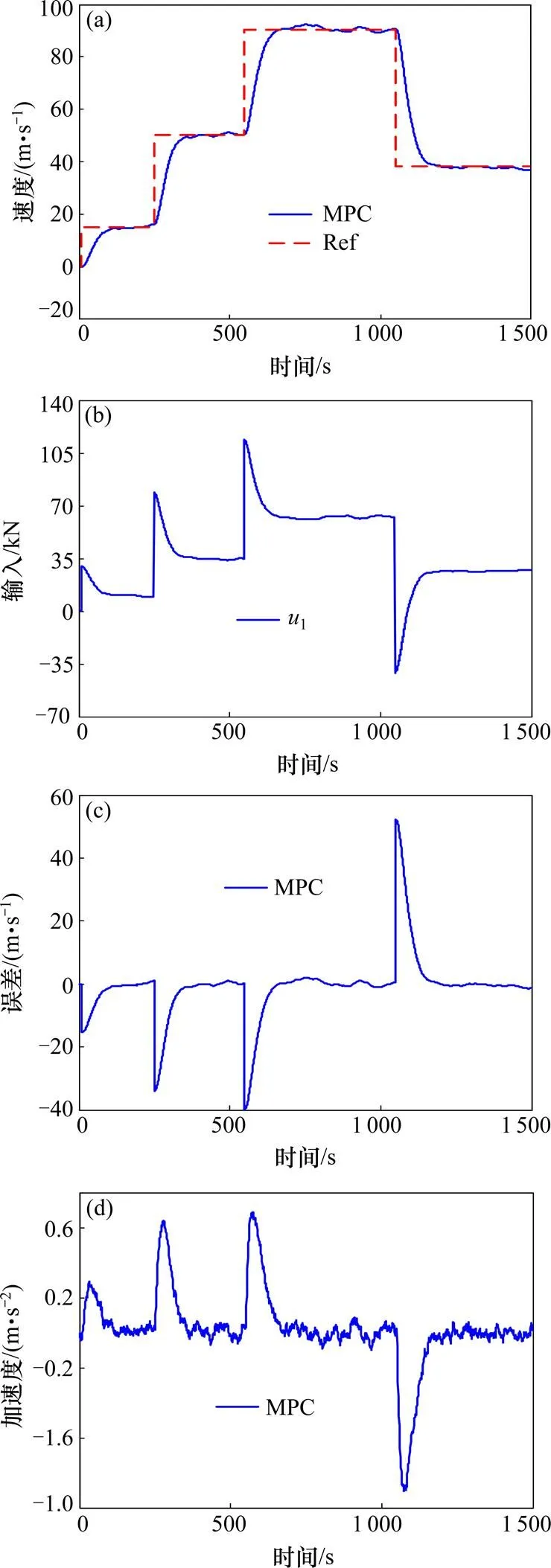
(a) 输出；(b) 输入；(c) 跟踪误差；(d) 加速度

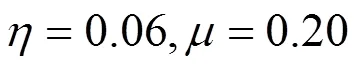
对比分析图3和图4可知，2种控制方法均能实现对列车既定速度进行一定程度的跟踪，传统模型预测控制时，列车实际运行速度波动较大，调整时间较长。对比跟踪误差可知，传统模型预测控制系统追踪误差比较大，采用神经网络反馈控制后，系统只在速度急剧变化处存在一定的跟踪误差，平稳运行后误差得到较大程度的消除，控制系统有较好的动态跟踪性能。同时，采用神经网络补偿控制后，系统的响应时间较快，这在一定程度上提高了系统跟踪性能。对比加速度结果图，也可看出基于神经网络反馈控制算法有更好的系统稳定性。

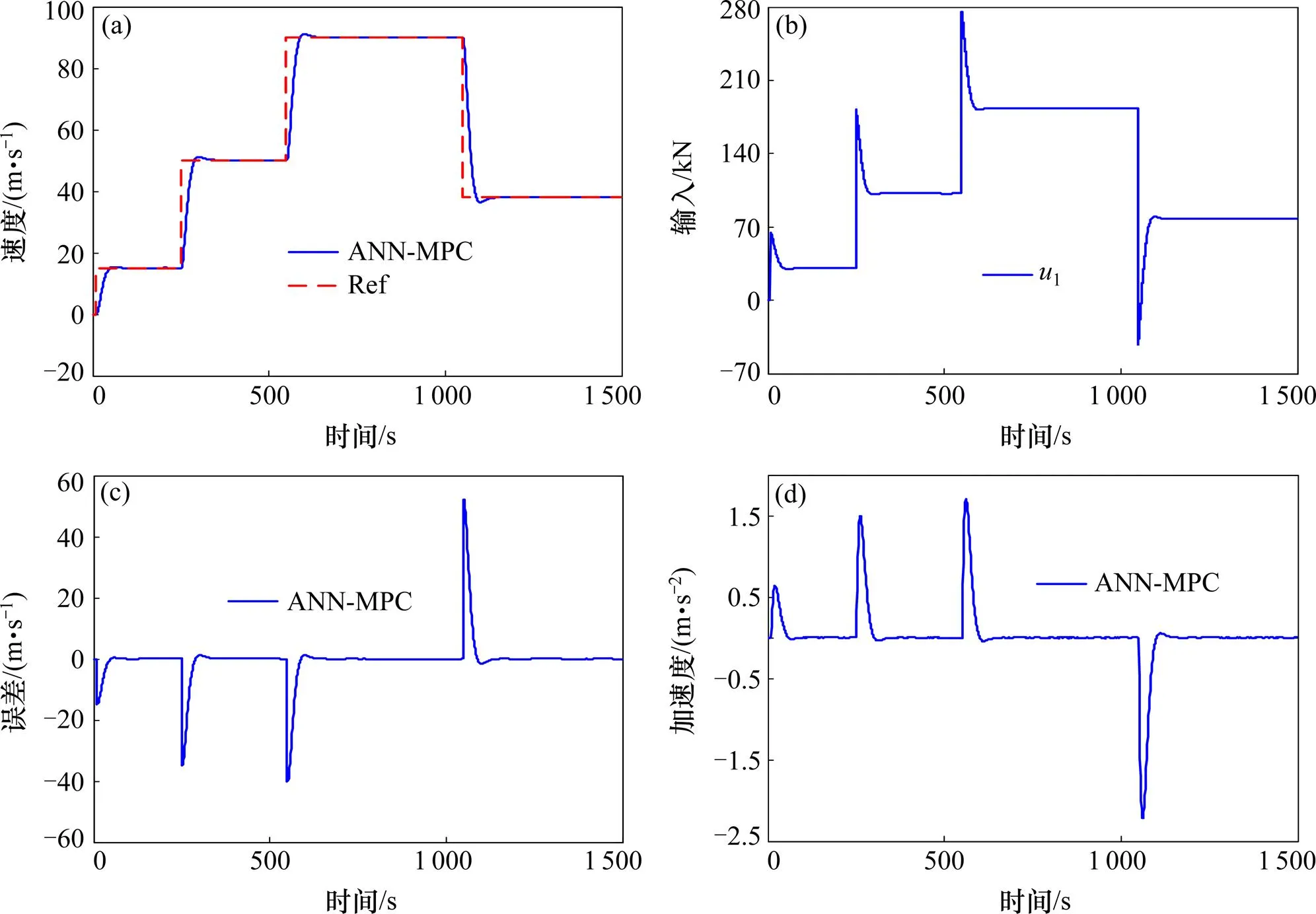
(a) 输出；(b) 输入；(c) 跟踪误差；(d) 加速度

5 结论

1) 针对列车运行过程的非线性特性，以及混合系统基于非线性系统建模的优越性，在列车运动学方程中引入离散变量，建立了混合系统列车运行模型，该模型可以更符合列车实际运行特性。

2) 转换列车模型为MLD形式，将列车运行约束条件整合入控制律求解中，确保在有效满足约束的条件下，提高列车控制器性能和列车运行效率。

3) 为了提高列车控制器追踪既定曲线精度，提出了一种基于神经网络反馈补偿控制、模型预测控制的列车速度追踪算法。该控制结构通过对实际速度与既定速度之间的系统误差进行学习，动态修正跟踪误差。

4) 通过数值仿真验证了所提控制器性能。在相同的预测控制参数下，相比模型预测控制，基于神经网络反馈补偿和预测控制的控制方法有较高的控制精度，预期效果更好，证明本文所提的基于神经网络反馈补偿的控制方法具有一定的可行性。

[1] Ganesan M, Ezhilarasi D, Jijo Benni. Hybrid model reference adaptive second order sliding mode controller for automatic train operation[J]. IET Control Theory & Applications, 2017, 11(8): 1222−1233.

[2] 董海荣, 高冰, 宁滨, 等. 基于模糊PID软切换控制的列车自动驾驶调速制动[J]. 控制与决策, 2010, 25(5): 794−800. DONG Hairong, GAO Bing, NING Bin, et al. Fuzzy-PID soft switching speed control of automatic train operation system[J]. Control and Decision, 2010, 25(5): 794−800.

[3] Gionata Cimini, Youngki Kim,­ ­Buz McCain, et al. Model predictive control for real-time position tracking of a catenary-free tram[J]. IFAC Papers Online, 2017, 1(50): 1000−1005.

[4] 余进, 钱清泉, 何正友. 两级模糊神经网络在高速列车ATO系统中的应用研究[J]. 铁道学报, 2008, 30(5): 52−56. YU Jin, QIAN Qingquan, HE Zhengyou. Research on application of two-degree fuzzy neural network in ATO of high speed train[J]. Journal of the China Railway Society, 2008, 30(5): 52−56.

[5] 董海鹰, 刘洋, 李欣, 等. 基于模糊神经网络预测控制的高速列车ATP研究[J]. 铁道学报, 2013, 35(8): 58−62. DONG Haiying, LIU Yang, LI Xin, et al. Study on high-speed train ATP based on fuzzy neural network predictive control[J]. Journal of the China Railway Society, 2013, 35(8):58−62.

[6] ZHANG Lijun, JIA Heming, QI Xue. NNFFC-adaptive output feedback trajectory tracking control for a surface ship at high speed[J]. Ocean Engineering, 2011(38): 1430−1438.

[7] Lewis F L, Shuzhi Sam Ge. Neural networks in feedback control systems[M]. New York: Mechanical Engineer’s Handbook: Instrumentation, Systems, Controls and MEMS, 2006.

[8] Kazuhiko Takahashi. Remarks on adaptive-type hyper complex-valued neural network-based feed forward feedback controller[C]// IEEE International Conference on Computer and Information Technology, 2017: 151− 156.

[9] LI Yongming, LI Tieshan, TONG Shaocheng. Adaptive neural networks output feedback dynamic surface control design for MIMO pure-feedback nonlinear systems with hysteresis[J]. Neurocomputing, 2016(198): 58−68.

[10] XU Zheng, HUANG Zhiwu, GAO Kai. Optimal operation of high-speed train using hybrid model predictive control[C]// 2017 29th Chinese Control and Decision Conference (CCDC). Chongqing, 2017: 3642− 3647.

[11] 王龙生. 基于多质点模型的高速列车自动驾驶预测控制[D]. 北京: 北京交通大学, 2016. WANG Longsheng. Predictive control for automatic operation of high-speed trains based on multi-point model[D]. Beijing: Beijing Jiaotong University, 2016.

[12] 李秀改, 高东杰, 王宇红. 基于混合逻辑动态模型的混杂系统预测控制[J]. 控制与决策, 2002, 17(3): 315− 319. LI Xiugai, GAO Dongjie, WANG Yuhong. Predictive control for hybrid system based on mixed logic dynamic model[J]. Control and Decision, 2002, 17(3): 315−319.

[13] 智力. 混合逻辑动态建模及其模型预测控制研究[D].杭州: 浙江大学, 2006. ZHI Li. Research on mixed logical dynamieal model and its model predictive control[D]. Hangzhou: Zhejiang University, 2006.

[14] 赵旭. 基于MLD模型的混杂系统预测控制研究[D]. 青岛: 中国石油大学(华东), 2010. ZHAO Xu. Research of hybrid predictive control based on MLD model[D]. Qingdao: China University of Petroleum (East China), 2010.

[15] LUO Lihua, LIU Hong, LI Ping, et al. Model predictive control for adaptive cruise control with multi-objectives: comfort, fuel-economy, safety and car-following[J]. Journal of Zhejiang University Science A (Appl Phys & Eng) 2010, 11(3): 191−201.

[16] 李国勇, 杨丽娟. 神经·模糊·预测控制及其MATLAB实现[M]. 北京: 电子工业出版社, 2013: 288−330. LI Guoyong, YANG Lijuan. Neural×Fuzzy×Predictive control and its MATLAB implementation[M]. Beijing: Electronic Industry Press, 2013: 288−330.

[17] 席裕庚. 预测控制[M]. 北京: 国防工业出版社, 2013: 100−129. XI Yugeng. Predictive control[M]. Beijing: National Defense Industry Press, 2013: 100−129.

[18] 冯瑞冬. 混合逻辑动态系统的预测控制器设计[J]. 控制工程, 2004, 11(4): 371−374. FENG Ruidong. Design of predictive control for mixed logical dynamic system[J]. Control Engineering of China, 2004, 11(4): 371−374.

Automatic train optimization operation based on hybrid system modeling predictive control

TANG Minan1, 2, WANG Panqi1

(1.School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. School of M echanical and Electronical Engineering, Lanzhou University of Technology, Lanzhou 730050, China)

Aiming at the problem that the automatic tracking speed of existing trains is not high, a model predictive control algorithm based on neural network feedback compensation control was proposed. According to the characteristics and advantages of the hybrid system, the auxiliary variables were introduced to establish the dynamic model of the hybrid train operation, which was convenient for solving the predictive control law with constraints. The secondary planning method was used to find the control action sequence that satisfies the various performance indicators of the train. The neural network feedback controller was used to learn the error between the system target speed and the actual speed and find a compensation control amount. The compensated control force was applied to the train system model. The simulation and experimental results show that the control structure includes compensation control strategy, which can reduce the system tracking error to a large extent, retain the advantages of model predictive control, and improve the control precision of the system.

hybrid system; neural network; model predictive control; automatic train operation; optimal operation

U281

A

1672 − 7029(2019)06− 1527 − 08

10.19713/j.cnki.43−1423/u.2019.06.024

2018−09−07

国家自然科学基金资助项目(61663021)；甘肃省高等学校科研资助项目(2017A-025)

汤旻安(1973−)，男，陕西勉县人，教授，博士，从事智能交通系统、智能控制研究；E−mail：tangminan@yahoo.com

(编辑 蒋学东)