车队作用下曲线连续梁桥动力响应分析

王贵春，孙瑜祥，张杰，吉喆，王亚欣

车队作用下曲线连续梁桥动力响应分析

王贵春，孙瑜祥，张杰，吉喆，王亚欣

(郑州大学 土木工程学院，河南 郑州 450001)

以桥面不平顺为激励，对某曲线连续梁桥进行数值分析，研究其在车队作用下的动力响应。采用傅里叶逆变换法模拟桥面不平顺，使用正态分布函数模拟随机车流，利用ANSYS编写迭代计算的APDL命令流求解车桥系统振动微分方程，针对不同工况分析桥梁动力响应。研究结果表明：就所研究工况，多车过桥比单车过桥引起的桥梁静位移小，而冲击效应大；路面不平度增加使桥梁竖向和扭转振动响应增大，但对横向振动影响很弱；曲率半径减小使桥梁竖向和横向振动更强烈，并使桥梁的静扭转角增大；曲率半径小于150 m时，对桥梁动力响应的影响显著。

曲线桥；汽车-桥梁耦合振动；数值模拟；动力响应

汽车−桥梁耦合振动一直是受到科研工作者广泛关注并致力研究的课题。车辆和桥梁之间的动力相互作用使车桥系统的动力响应求解变得复杂。通常的做法是建立车、桥子系统的振动微分方程并进行联立迭代求解。从早期对匀速移动常量力作用下简支梁振动问题的分析，到现今有限元软件和数值模拟方法的广泛运用，车桥耦合振动问题的研究经历了长时期的发展。车辆和桥梁模型的模拟越来越精确，考虑的因素越来越多，桥梁桥型也从一开始的简支梁桥发展成各种桥型。随着大型立交系统的建设，曲线梁桥近年来发展迅速。曲线梁桥易发生扭转振动，急需就相关问题做进一步研究。Tan等[1]在对等截面曲线梁的研究中考虑桥梁惯性力和瞬态荷载。美国联邦公路管理局组建的研究组对曲线梁进行了一系列理论和试验研究，基于其研究成果以及Maryland大学的相关工作，形成了曲线梁应力设计准则和钢弯梁的临时设计规程[2]。HUANG等[3−4]采用具有11个自由度的非线性模型模拟移动车辆，以国家规范中的功率谱密度函数模拟4个桥面等级进行车桥耦合振动分析，用有限元法研究了多梁式I型梁和曲线薄壁箱梁在车辆荷载作用下的动力响应特征。黄新艺[5]基于剪力柔性梁格理论提出适用于曲线梁桥动力分析的三梁式模型，对一座曲线梁桥动力响应进行了数值模拟计算，同时进行实验验证，得出很多有价值的结论。在以往的研究中，虽然有对车流作用下车桥耦合振动的分析，但对曲线梁桥的研究，鲜有多车辆荷载作用情况的报道。黄新艺[5]的研究包括了纵向车辆数对振动的影响，最大车辆数为3辆，是作为特殊工况来研究的。安忠海[6]在对曲线钢—混凝土组合梁桥的研究中加入“行车数量”这一影响因素，但只对比了1辆车和2辆车作用下的桥梁响应。上述研究不能完全体现出多车辆作用下曲线梁桥车桥耦合振动规律。在此，本文以某曲线连续梁桥为研究对象，分析在多车辆作用下的桥梁动力响应。

1 计算模型及求解方法

将车辆模型简化为三维多刚度体系，用有限元法模拟桥梁结构，假设桥面与车轮间为点接触，且车辆与桥面间没有相对横向位移[7]。

1.1 计算模型

1.1.1 桥梁模型的建立

选取一座三跨曲线连续梁桥作为研究对象，桥跨为40 m+50 m+40 m，主梁横截面和桥跨布置如图1和图2所示。

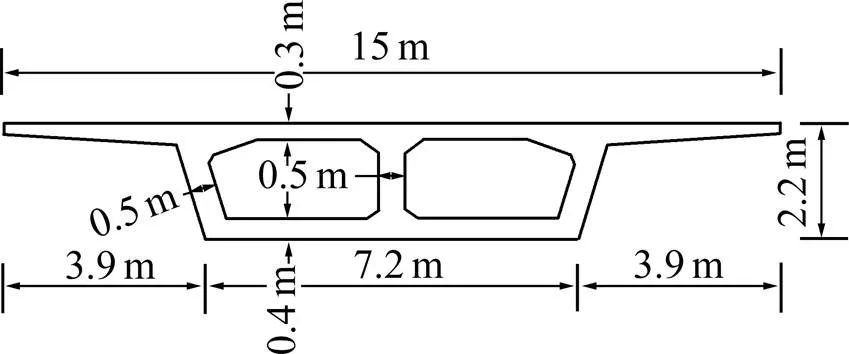
图1 箱梁横截面示意图

图2 桥跨分布示意图

1.1.2 车辆模型的建立

建立三轴9自由度空间整车模型[8]，车体考虑浮沉、侧倾和俯仰3个自由度，车轮仅考虑竖向位移的自由度。车体三维模型如图3所示，其中m为车体质量；m1~m6为6个车轮(包括车悬架)的质量；k1~k6和c1~c6分别为车悬架刚度和阻尼；k1~k6和c1~c6分别为轮胎刚度和阻尼；z1~z6为6个车轮质心处竖向位移；z表示车体质心处竖向位移；表示车体质心处俯仰角位移；表示车体质心处侧倾角位移。

车辆参数：m为24 990 kg；m1和m2为335 kg；m3~ m6为670 kg；k1和k2为718 kN/m；k3~k6为1 652 kN/m；c1~c6为2.4×105kg/s；k1和k2为2 680 kN/m；k3~k6为4 809 kN/m；c1~c6为2 340 kg/s。

1.1.3 桥面不平顺的模拟

桥面不平顺的模拟方法较多，包括三角级数法、白噪声法等。其中傅里叶逆变换法思路明确，便于操作，且利用这种方法得到的路面不平度，其对应的功率谱密度可以与给定的功率谱密度一致[9]，因此，选取傅里叶逆变换法进行桥面不平顺的数值模拟。路面不平度的功率谱密度可用下式 拟合：

式中：n为空间频率；n0为参考空间频率，取0.1 m−1；Gx(n0)为参考空间频率下的路面功率谱密度，称为路面不平度系数。ω为频率指数，它决定路面功率谱密度的频率结构，其值为2。

根据统计意义上的汽车主要频率范围选择合适的有效空间频率范围。对一段长度为的路面进行离散采样。设样本数为，x(=0,1,…,−1)为路面不平度的采样数据，为虚数单位，则x的离散傅里叶变换为：

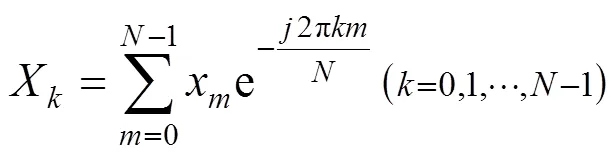
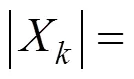
式中：xm即为桥面不平顺的数值。图4为利用上述方法模拟出的B级桥面不平顺样本函数。

1.2 振动微分方程

根据前文所述车辆模型和桥梁模型建立车辆和桥梁振动微分方程[9]。

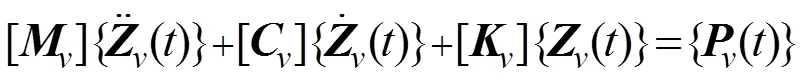
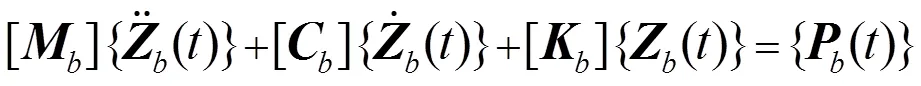
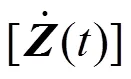
车辆和桥梁动力耦合作用通过车轮与桥面接触点处的位移协调条件和作用力的平衡条件实现。

1) 位移协调条件：假设轮胎与路面始终保持紧密接触且不脱离，则路面与车轮的相对竖向位移为

式中：z为路面在其与第个车轮接触点处的竖向位移；z为第个车轮的竖向位移；r()为第个车轮与路面接触点处的路面不平顺值。

2) 力的平衡条件：轮胎与路面接触点的相互作用力遵循牛顿第三定律，即车辆和路面之间的作用力大小相等、方向相反：

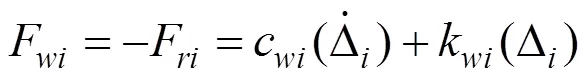
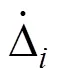
1.3 振动微分方程的求解及收敛控制

对上述振动微分方程使用Newmark-β法进行分离迭代求解，利用有限元软件ANSYS的前、后处理和求解能力，使用APDL语言进行二次开发，编写命令流进行求解。采用位移收敛准则控制计算过程，即

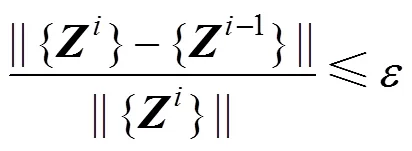
2 数值分析

用上述方法计算桥梁的动力响应，车重为30 t，车速为10 m/s，桥梁结构阻尼比为0.02，车辆荷载无偏心。多车过桥时，使用正态分布函数模拟随机车流。统计信息表明，车辆间距具有随机特性，服从对数正态分布规律。设是车辆间距，=ln， 则有

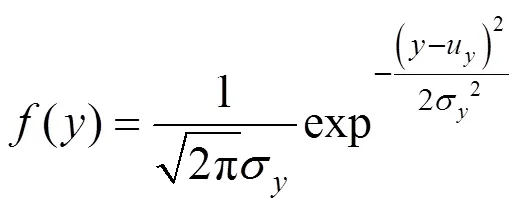
引入冲击系数的概念：冲击系数是指汽车通过桥梁时对桥梁结构产生的动力效应增大系数，即汽车荷载的动力影响[10]。冲击系数的表达式如下：

2.1 路面不平度的影响

路面不平度是车桥耦合振动的重要影响因素，在此分别对单车、多车过桥时路面不平度对桥梁动力响应的影响进行分析和对比。

2.1.1 路面不平度对桥梁竖向振动的影响

多车、单车过桥时中跨跨中竖向位移时程曲线如图5~6所示。

图5 多车作用下中跨跨中竖向位移时程曲线

对照图5和图6可知，与单车过桥时的情况不同，多车过桥时，竖向位移响应呈现出一定的周期性，这个周期和各个车辆运行至桥跨跨中的时间有关。各周期内的位移幅值出现在某辆车行驶到该跨跨中前后。

图7为中跨和边跨跨中竖向位移幅值。由图7可知，多车运行时，中跨跨中的竖向位移幅值反而小于单车运行时的情况。这是因为前后车辆作用使桥梁中跨产生的正位移抵消了中跨上车辆作用产生的负位移，从而造成多车运行时桥梁的静位移小于单车运行时的情况，并影响到总体竖向位移。而对于边跨的情况，多车作用造成的静位移减小不像中跨的情况那么明显，而多车作用造成的动力效应较为明显，因而多车作用时其总位移值大于单车作用的情况。

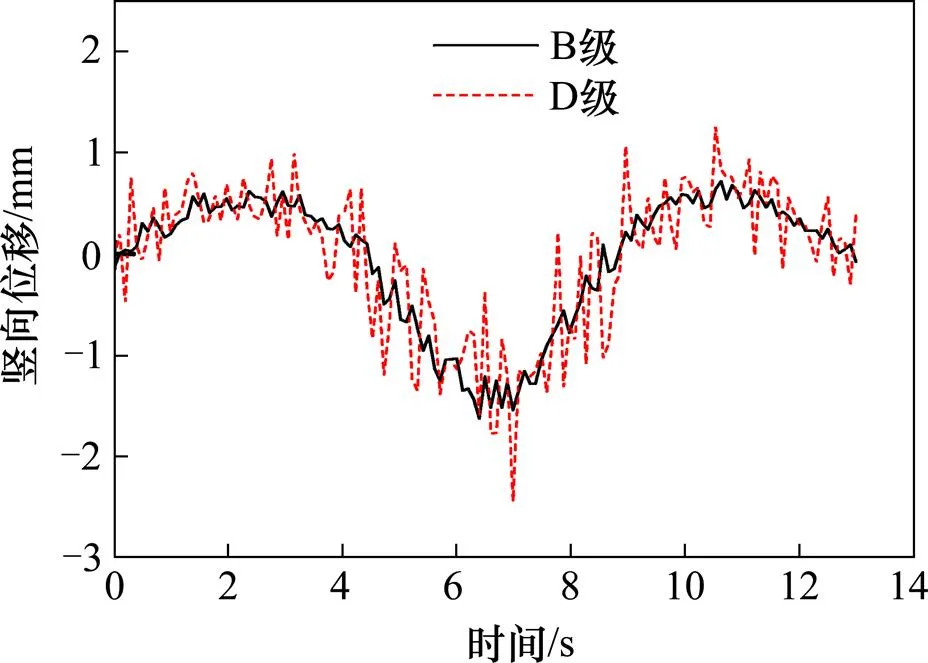
图6 单车作用下中跨跨中竖向位移时程曲线

图7 竖向位移幅值曲线

图8为中跨和边跨跨中竖向位移冲击系数。由图8可知，不论是中跨还是边跨，多车运行时竖向振动位移冲击系数大于单车运行的情况。以B级路面不平顺为例，在中跨跨中，单车运行时竖向振动位移冲击系数为0.154，多车运行时为0.329，比单车运行时增大113.63%。这说明多车运行时，不同车辆造成的振动效应叠加，会使车桥耦合振动的动力响应增大。

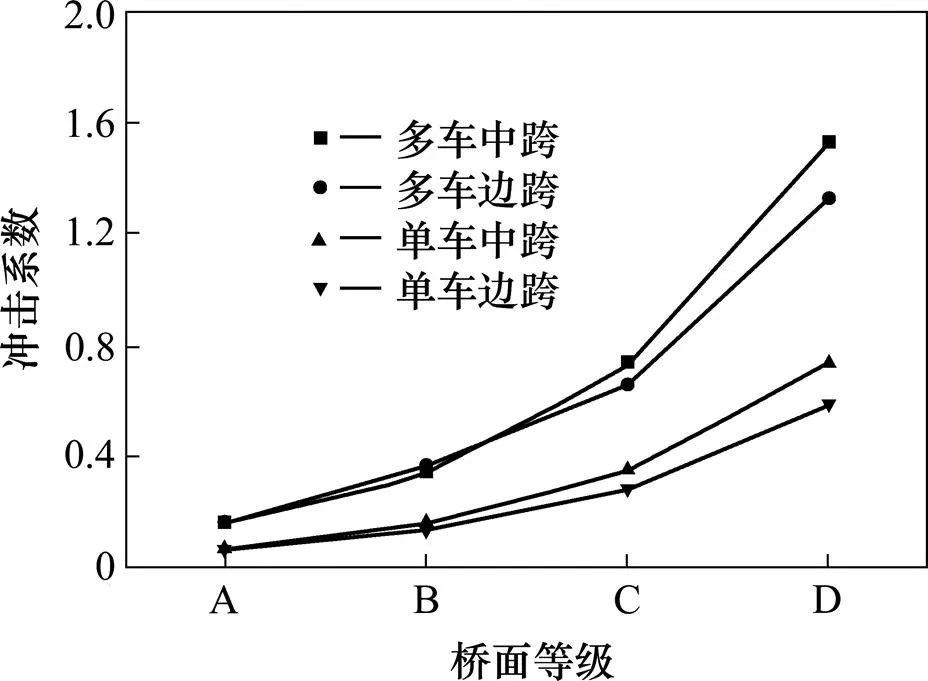
图8 竖向位移冲击系数曲线

需要注意的是，关于中跨与边跨竖向振动幅度受车辆运行方式的影响，需要考虑桥梁跨度和车辆间距等因素的作用。随着桥跨与车距组合的变化，振动的叠加效果可能会出现多种不同的情况。在某些情况下，多车运行时的桥梁竖向振动可能比单车运行时的振动强烈得多。除了振动位移幅值的变化外，桥梁各跨跨中竖向振动位移时程曲线的形式也可能会出现一些变化。

此外，由图7和图8可知，随着路面不平度的增加，桥梁竖向振动位移幅值和冲击系数都迅速增大。以冲击系数为例，多车运行时，在A级路面不平顺下，中跨跨中竖向振动位移冲击系数为0.252，而B，C和D 3个不平顺等级对应的冲击系数分别比前一级增大57.94%，112.31%和62.96%，增大非常明显。

2.1.2 路面不平度对桥梁扭转振动的影响

图9为多车作用下中跨跨中扭转角时程曲线。

图9 多车作用下中跨跨中扭转角时程曲线

由图9可以看到，多车过桥时，桥跨跨中的扭转角响应随时间变化的规律与竖向位移的情况 相似。

各个路面等级对应的中跨和边跨跨中扭转角幅值及其冲击系数变化情况如图10~11所示。

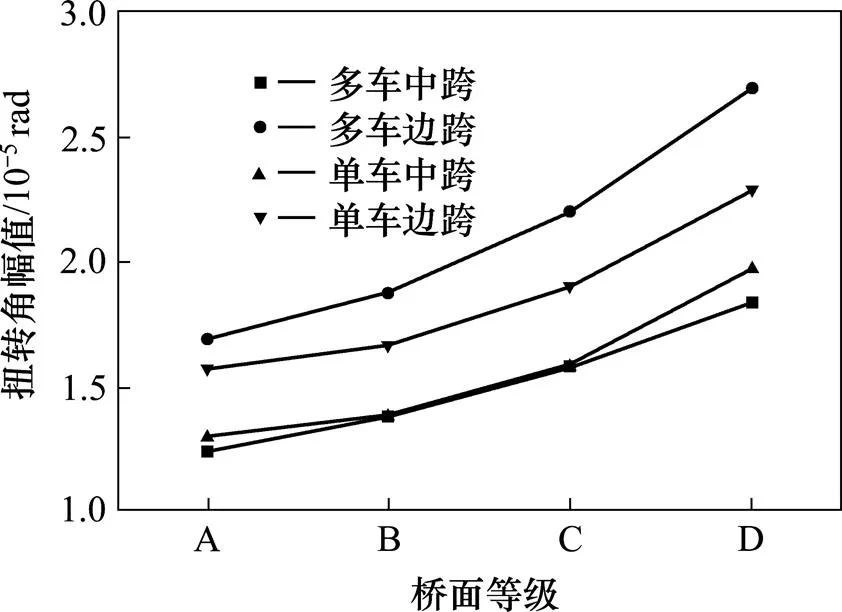
图10 扭转角幅值曲线

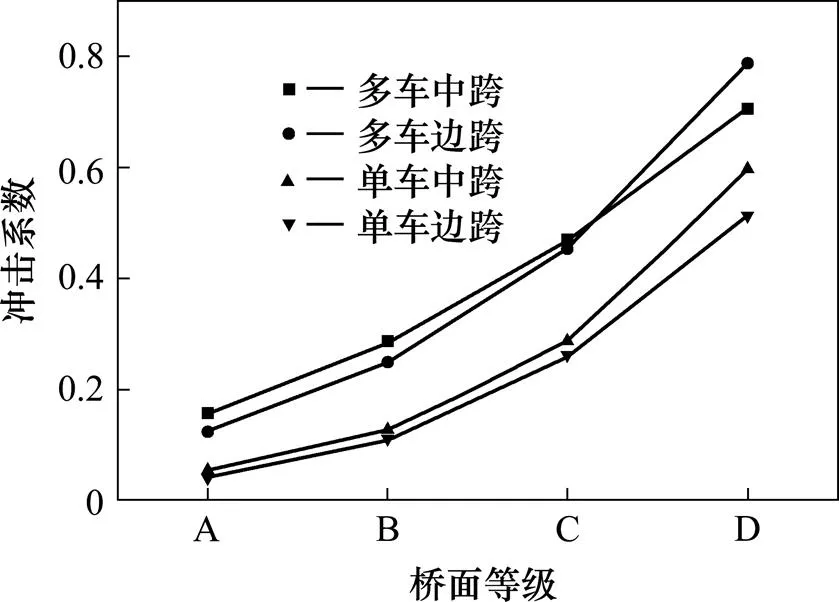
图11 扭转角冲击系数曲线

由图10可知，扭转振动响应，数值上的变化规律与竖向振动也是相似的，都表现为多车运行时动力响应比单车的情况强，静力响应比单车的情况弱。在中跨，多车作用时的扭转角幅值略小于单车作用的情况。在边跨，多车作用时的扭转角幅值大于单车作用的情况。由图11可知，不论是中跨还是边跨，多车运行时扭转振动角位移冲击系数大于单车运行的情况。

同样，随着路面不平度的增大，桥梁的扭转振动也变得越来越强烈。

2.1.3 路面不平度对桥梁横向振动的影响

图12为多车作用下中跨跨中横向位移时程 曲线。

图12 多车作用下中跨跨中横向位移时程曲线

由图12可见，横向振动位移时程曲线在形式与竖向振动的情况相似。但需要注意的是，它们的本质是不同的，静载作用下，桥梁存在竖向位移，但没有横向位移。图13为横向振动位移幅值随桥面等级变化的情况。

图13 横向振动位移幅值曲线

由图13可见，桥梁横向振动同样存在类似规律，即中跨多车运行时振动位移幅值小于单车运行的情况，边跨多车作用下振动位移幅值略大于单车作用的情况。

此外，不论是从折线图还是位移时程曲线都可以看出，随着路面不平度的增大，桥梁的横向振动响应并没有明确的变化趋势，变化幅度也非常微弱，约是竖向振动的3.5%左右，可以认为桥面不平顺对曲线桥的横向振动的影响很小。

2.2 桥梁曲率半径的影响

曲率半径是曲线桥的重要几何参数，正是由于结构初始曲率的存在，桥梁在不受偏心荷载作用时仍会出现扭矩和扭转角。选取50~350 m范围内的一系列曲率半径值对桥梁各项动力响应进行分析，同时计算同跨度的直线桥(即曲率半径为∞)的动力响应作为参照。鉴于前面已对单车运行和多车运行时桥梁动力响应的差别进行了研究，在此只讨论多车运行时桥梁动力响应随曲率半径的变化规律。车速取10 m/s，路面不平度为B级。

2.2.1 曲率半径对桥梁竖向振动的影响

图14为中跨跨中竖向位移时程曲线，图15为位移冲击系数随曲率半径变化的情况。

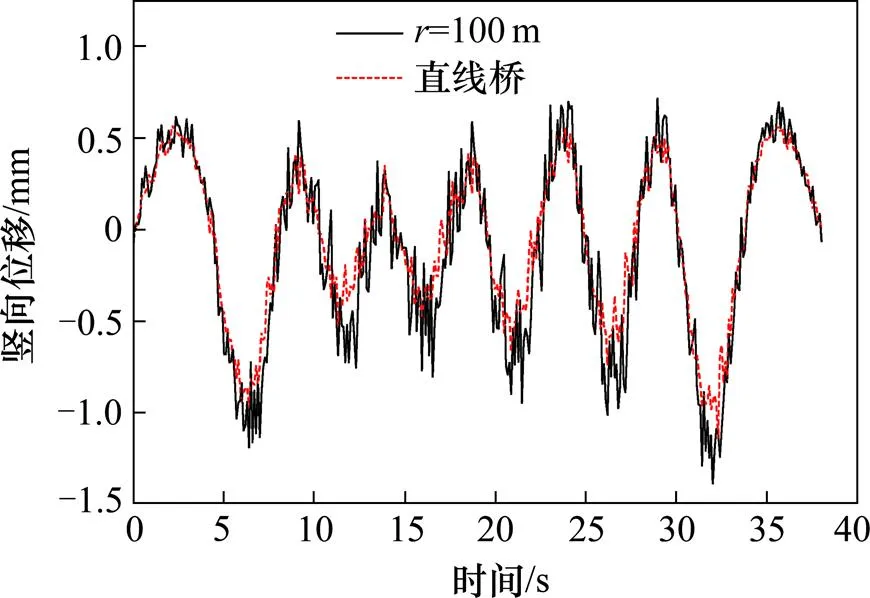
图14 中跨跨中竖向位移时程曲线

图15 竖向位移冲击系数曲线

由图15可知，随着曲率半径的增大，桥梁竖向振动响应总体呈现减小的趋势，在曲率半径小于150 m时变化幅度很大，曲率半径大于150 m时变化幅度减缓。这说明当曲率半径增大到一定程度后对桥梁的动力响应影响很弱。

2.2.2 曲率半径对桥梁扭转振动的影响

图16为中跨跨中扭转角位移时程曲线，图17~18为扭转角幅值和位移冲击系数随曲率半径变化的情况。

图16 中跨跨中扭转角时程曲线

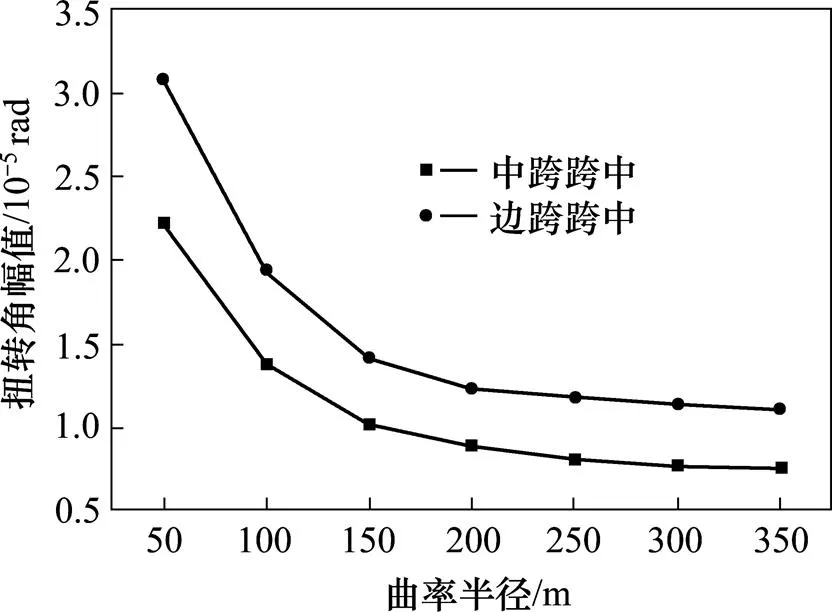
图17 扭转角幅值曲线

图18 扭转角冲击系数曲线

由图17~18可见，扭转振动角位移幅值随曲率半径增大而减小的幅度很大，而振动扭转角冲击系数减小的幅度很小。这说明曲率半径的减小会使桥梁静扭转角增大，但并不会造成更大的扭转冲击效应。另外，扭转角幅值和冲击系数随曲率半径的变化也是在半径小于150 m时较明显，在半径大于150 m时较微弱。

2.2.3 曲率半径对桥梁横向振动的影响

图19~20为中跨跨中横向位移时程曲线和位移幅值随曲率半径变化的情况。

图19 多车作用下中跨跨中横向位移时程曲线

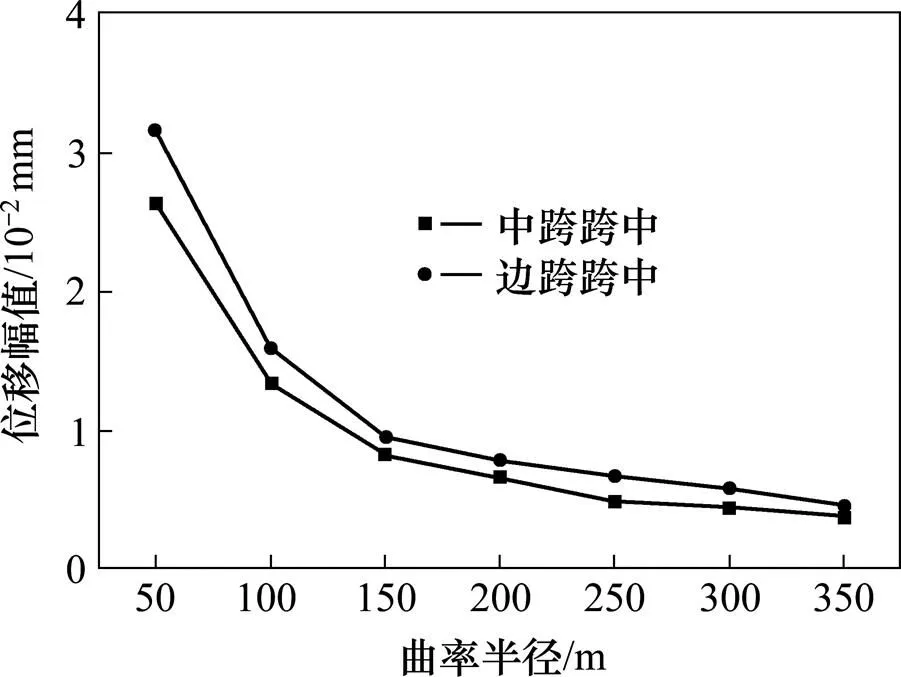
图20 横向振动位移幅值曲线

由图20可知，随着曲率半径的增大，桥梁横向位移大幅度减小，在曲率半径小于150 m时变化尤其明显。曲率半径为100 m时，中跨跨中横向振动位移幅值为1.339×10−2 mm，曲率半径为50 m时幅值为2.640×10−2 mm，增大了197.16%。在曲率半径大于150 m时，其变化幅度也大于竖向振动位移幅值的变化幅度，曲率半径为250 m时，中跨跨中横向振动位移幅值为0.488×10−2 mm，曲率半径为200 m时幅值为0.659×10−1 mm，增大了35.04%，可见曲率半径对桥梁的横向振动位移影响很大。

3 结论

1) 基于本文的研究工况，在桥面不平顺的激励下，当相邻桥跨有车辆运行时，多车过桥比单车过桥时的桥梁静位移减小，而冲击效应增大。

2) 随着路面不平度的增大，桥梁竖向振动和扭转振动的各项动力响应均呈现明显增加的趋势。路面不平度对桥梁横向振动的影响很弱。

3) 随着曲率半径减小，桥梁动力响应增大。曲率半径小于150 m时，其对动力响应的影响显著；大于150 m时，影响较弱。

4) 关于扭转振动，桥梁扭转角受曲率半径的影响较为敏感，而冲击系数受到的影响很小。

[1] Tan C P, Shore S. Dynamic response of a horizontally curved bridge[J]. Journal of the Structural Division, ASCE, 1968, 94: 761−781.

[2] American Association of State Highway and Transportation Officials. AASHTO LRFD bridge design specifications[S]. 2004.

[3] HUANG Dongzhou, WANG Tonlo, Shahawy M. Dynamic behavior of horizontally curved I-girder bridges[J]. Computers and Structures, 1995, 57(4): 703− 714.

[4] HUANG Dongzhou, WANG Tonlo, Shahawy M. Vibration of horizontally curved box girder bridges due to vehicles[J]. Computers and Structures, 1998, 60: 513− 528.

[5] 黄新艺. 混凝土连续曲线梁桥在车辆荷载下的动力响应研究[D]. 哈尔滨: 哈尔滨工业大学, 2008. HUANG Xinyi. Dynamic response research of continuous curved concrete bridges under moving vehicles[D]. Harbin: Harbin Institute of Technology, 2008.

[6] 安忠海. 车辆荷载作用下曲线钢—混凝土组合箱梁桥的动力性能研究[D]. 西安: 长安大学, 2008. AN Zhonghai. Study of the structural dynamic behavior of curved composite concrete steel box girder bridges based on the vehicle load[D]. Xi’an: Chang’an University, 2008.

[7] 王贵春, 李武生. 斜拉桥在多车辆作用下的动力响应分析[J]. 桥梁建设, 2014, 44(6): 81−87. WANG Guichun, LI Wusheng. Analysis of dynamic response of cable-stayed bridge under action of multiple vehicles[J]. Bridge Construction, 2014, 44(6): 81−87.

[8] 赵露薇. 大跨度公路钢管混凝土拱桥车桥耦合振动分析[D]. 郑州: 郑州大学, 2017. ZHAO Luwei. The analysis of vehicle-bridge coupling vibration of CFST[D]. Zhengzhou: Zhengzhou University, 2017.

[9] 刘献栋, 邓志党. 基于逆变换的路面不平度仿真研究[J]. 中国公路学报, 2005, 18(1): 122−126. LIU Xiandong, DENG Zhidang. Study of simulation of road roughness based on inverse transform[J]. China Journal of Highway and Transport, 2005, 18(1): 122−126.

[10] JTG D60, 公路桥涵设计通用规范[S]. JTG D60, General specifications for design of highway bridges and culverts[S].

The analysis on dynamic responses of curved continuous bridge due to vehicle flow

WANG Guichun, SUN Yuxiang, ZHANG Jie, JI Zhe, WANG Yaxin

(School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China)

A curved continuous bridge was analyzed to research its dynamic responses due to vehicle flow on the basis of taking pavement roughness as excitation. Using the inverse Fourier transform method to simulate the value of road roughness, the iterative calculation command stream to solve differential coupled vibration equations of vehicle-bridge systems was compiled in APDL language in ANSYS computer software to analyze bridge dynamic responses separately for different working conditions. The results indicate that the static displacements due to vehicle flow are less than those due to single vehicle and the impact effects due to vehicle flow are more than those due to single vehicle in the view of research conditions; the increment of road roughness will make the vertical and torsional dynamic responses of bridge increase and it has little influences on lateral vibration; The decrement of the radius of curvature will make the vertical and horizontal vibration of the bridge be more severe and increase the static twist angle of the bridge, and the case is more especially significant when the radius is less than 150 m.

curved bridges; vehicle-bridge coupled vibration; numerical simulation; dynamic response

U441.3；448.21

A

1672 − 7029(2019)06− 1476 − 08

10.19713/j.cnki.43−1423/u.2019.06.017

2018−08−29

国家自然科学基金青年资金资助项目(51408554)

王贵春(1962−)，男，辽宁黑山人，教授，博士，从事桥梁结构研究；E−mail：guichunwang@163.com

(编辑 阳丽霞)