灌区水量调度中闸门流量-开度模型研究
易汉文,宁 芊,赵成萍
(1.四川大学 电子信息学院,四川成都610065;2.电子信息控制重点试验室,四川成都610036)
随着科技的迅猛发展,灌区管理控制智能化成为必然趋势。很多灌区是靠闸门调度来控制水位和流量的,渠道闸门开启和关闭往往是依据整体水量的调配,传统方式多数是基于以往水文资料和经验人工制订配水计划,在实际操作过程中依据实际来水量情况由操作人员进行动态调配,以实现水量的动态配给。这种以个人经验为主的方法,依赖于操作人员的工作水平,从而使得配水随机性增大,难以实现整体调度的自动化控制,同时也不利于灌区的统一管理。若建立模型,根据期望的流量自动计算出闸门开启和关闭时机,就能解决上面的问题。基于智能化的理念,笔者采用两种建模方法,一种是基于水力学公式的单孔闸门流量-开度关系;另一种是基于神经网络算法或其他机器学习算法构建的流量-开度模型。对于第一种方法,在实际建模中如果缺少河道及相应的水位信息[1],将无法建立合适的模型;该方法还需要实际的闸门类型、渠道参数方能建立模型。第二种方法不依赖实际环境,计算较为简单,但历史数据的丰富程度决定了建模结果的好坏。本文以都江堰灌区闸门联合调度为背景,对各分水枢纽的闸门分别建模,并对比各闸门建模效果,为模型的选择提供依据。
1 试验灌区简介
都江堰内江水系四大干渠分别为蒲阳河、柏条河、走马河和江安河。都江堰灌区内江水流首先经过鱼嘴流入宝瓶口,然后流到仰天窝闸门处。在仰天窝闸处,分别流向蒲柏闸和走江闸方向。流向蒲柏闸的水分别流向蒲阳河和柏条河;流向走江闸的水分别流向走马河和江安河。都江堰内江闸群分布见图1,其中:仰天窝闸有6个闸孔,3孔流向蒲柏闸方向,3孔流向走江闸方向;蒲柏闸有7个闸孔,分为蒲阳河4孔、柏条河3孔;走江闸有8个闸孔,分为走马河5孔、江安河3孔。根据数据分布以及现场环境的不同,分别建立各分支枢纽的流量-开度模型,对比模型优劣。
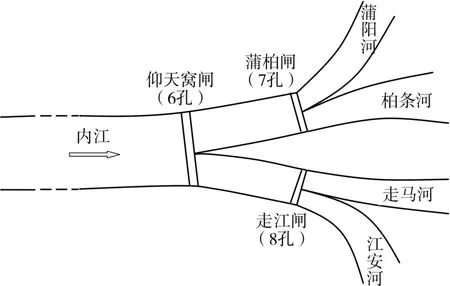
图1 都江堰内江闸群分布
2 流量-开度模型构建
2.1 基于水力学关系的单孔闸门流量-开度模型
都江堰闸门多为宽顶堰型闸门,将闸门出流分为自由出流和淹没出流两种方式。根据两种方式的流量-开度数学公式[2],首先建立单孔的流量-开度模型,再扩展到三孔以及多孔流量-开度模型。两种模型的建立都是基于Matlab Simulink仿真结果[3]。
设H为闸前水深,e为闸孔开度。当水流行近闸孔时,在闸门的约束下流线发生急剧弯曲;出闸后,流线继续收缩,并在闸门下游(0.5~1.0)e处出现水深最小的收缩断面。收缩断面的水深一般小于临界水深hk(渠道的临界水深与底坡坡降没有关系,只与渠道的流量及形状尺寸有关),水流为急流状态;而闸后渠道中的下游水深ht一般大于临界水深hk,水流呈缓流状态;水流从急流到缓流时发生水跃,水跃位置随下游水深ht而变化。
根据有关资料[2],闸孔自由出流流量的水力计算公式如下(其中流量系数μ取南京水利科学研究院的经验公式计算结果):
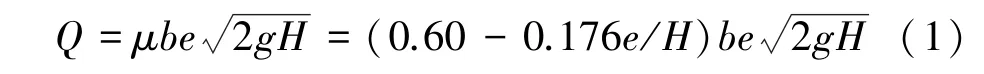
闸孔淹没出流流量的水力计算公式为
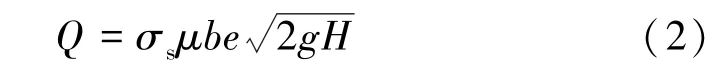
式中:b为闸门宽度;g为重力加速度;σs为淹没系数,σs值与下游水深ht、收缩断面水深的共轭水深h″c、闸前水深H有关。
模型实现流程见图2。
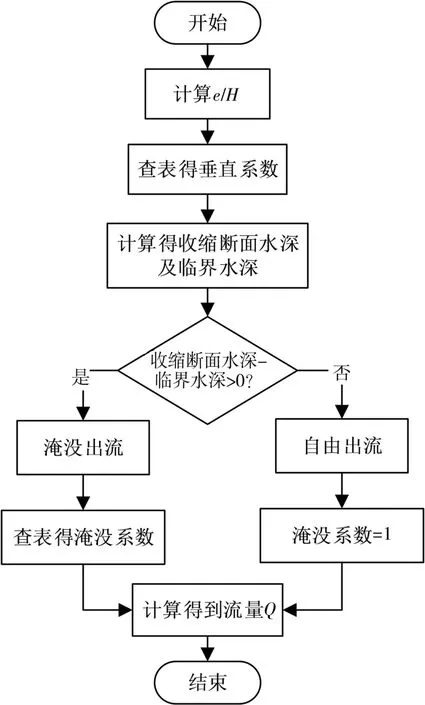
图2 单孔闸门流量-开度模型流程
2.2 基于水力学关系的多孔闸门流量-开度模型
单孔闸门流量开度模型扩展到多孔闸门时,在灌区调度实际允许的误差范围内,可以认为多孔闸门出流的总流量Q就是该闸门各个闸孔所需的流量之和,即
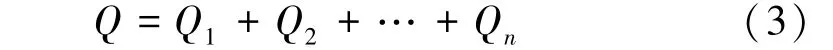
式中:Q1、Q2、…、Qn分别为各单孔出流量。
都江堰灌区闸门多为三孔闸门,也有少数闸门为三孔以上,如蒲阳河为4孔、走马河为5孔。从获得的历史数据来看,蒲阳河2号和3号闸孔开度相同的情况约占80%,最大差值为0.5 m,根据实际情况,将2号和3号闸孔看作一个整体,同开同关。走马河在洪汛期2号、3号和4号闸孔的开度比较大,大于水面高度;枯水期,闸门开度较小。走马河2号、3号和4号闸孔的开度相似度为80%左右,最大差值为0.5 m,可将2号、3号和4号闸孔看成一个整体。
从上述等效过程来看,在试验灌区建立开度模型时,对于部分多孔闸门可采用三孔闸门的流量开度模型。
2.2.1 三孔闸门启闭规则
为了使闸门的开启和关闭更加安全可靠,遵循动闸最少原则,在实际操作过程中应遵守一定的启闭规则。都江堰闸门主要的启闭规则[3]是:考虑到闸门提升时,靠近河岸的闸门出水会受到影响,当需要增加闸孔出流量时,先判断哪些闸门在水面以下,当前开度最大的应最后提升至合适位置;若闸门的开度近似相等,由于中间闸门出水受河岸影响小,因此先提升中间闸门,然后提升不靠近河岸的闸门,最后才考虑靠近河岸的闸门;当需要减小闸孔出流量时,应判断哪些闸门开度不是零,开度最小的最后下降至合适位置,若闸门的开度都相同,应先降低靠近河岸的边孔,最后减小中间闸孔开度。
2.2.2 三孔闸门流量-开度模型建立
在文献[3]的公式讨论中,只能根据开度、水位等信息求得当前的过闸流量。但在实际调度过程中总是希望得到一个满足期望流量的开度。为了求得合适的开度,不能简单对原来的公式进行反向求解。本文选取一组分布较为均匀的数据(记录了单个闸孔的闸门开度、过闸流量等),拟合出一条流量与开度的关系曲线。对于三孔以及多孔闸门,也可以用该关系曲线求出各闸门开度。依据启闭规则与关系曲线得到模型流程(见图 3),其中:error为允许误差范围, e1、e2、e3为按照启闭规则排序后的闸孔顺序及开度大小,QC为当前流量,QH为期望流量,Q1为e1调后当前流量,Q2为e1、e2调后当前流量,Q3为 e1、e2、e3调后当前流量,ΔQ1、ΔQ2、ΔQ3为当前流量差。
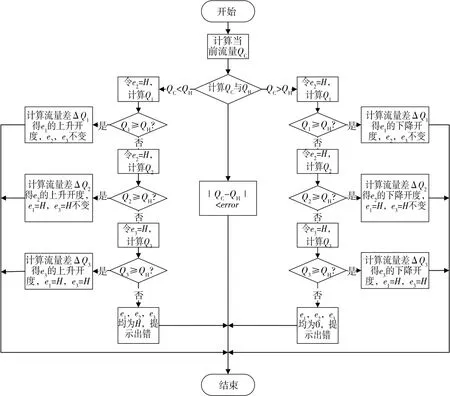
图3 三孔闸门流量-开度模型流程
2.3 基于机器学习的流量-开度模型
2.3.1 神经网络模型
人工神经网络的优点在于具有逼近连续非线性函数的能力,而且能从大量历史数据中获取知识,当有新的输入产生时,能对结果有较好的预测。神经网络模型的结构种类较多,例如感知器、Hopfield网络、BAM网络、径向基神经网络、自组织特征映射神经网络[4]等。BP神经网络应用广泛,由输入层、隐含层、输出层构成。其中隐含层的层数越多,计算过程越复杂,输入层和输出层权值的激励函数,正是不断反复通过输入信号的正向传递与误差的反向传递这一过程,实现对权值的修改[5]。误差反向传递使实际值与期望值的均方差达到最小,由此神经网络具有获取知识的能力。由式(1)可知,影响闸门过闸流量的主要因素为闸门开度、闸门宽度、闸前水深,反向求解过程中影响开度的因素也易知。本文以闸门开度、闸门宽度、闸前水深为BP神经网络的3个输入因子,以3个闸孔的开度为输出因子,建立3层神经网络模型(见图4)。
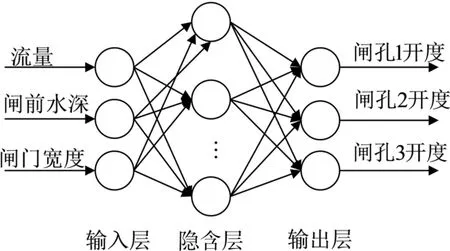
图4 闸门流量-开度神经网络模型
LM算法[6-8]是一种利用标准的数值优化技术的快速算法,是梯度下降法与高斯-牛顿法的结合,也可以称为是高斯-牛顿法的改进形式,既有高斯-牛顿法的局部收敛性,又具有梯度法的全局特性。由于LM算法利用了近似的二阶导数信息,因此LM算法比梯度法快得多,解决了BP算法收敛速度慢、易陷入局部最优的问题[9]。
2.3.2 SVM模型
支持向量机(SVM)[10-11]起初是用于解决模式识别问题[7],由 Vapnic[12-13]于 20 世纪 90 年代提出,具有良好范化性、适用于小样本、数学表达简捷等优点,被广泛应用于线性和非线性曲线拟合当中,并在许多实际问题中取得优良成果。大多数传统的SVM模型的输出为单个,模型的核函数为一个。就本研究的数据来看,若用SVM来建立模型,则要求采用多个核函数方法来训练模型[14-15]。考虑用闸后流量、闸门宽度、闸前水深作为模型的3个输入,3个闸孔的开度作为输出,得到多输出SVM 结构图(见图5),其中:x1、x2、x3为输入特征值,K(x,xi)为核函数,a 为偏置,S 中间值,y为输出特征值。
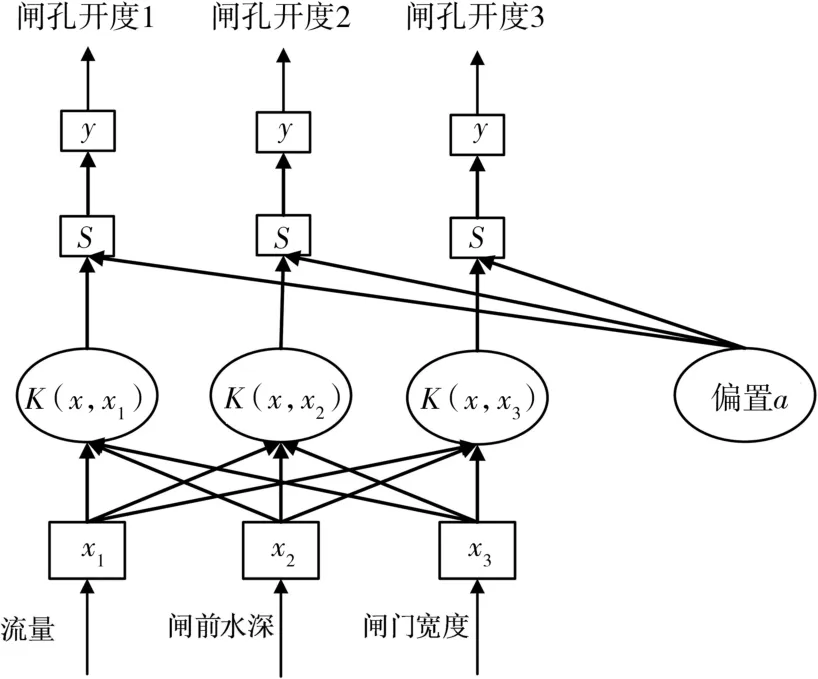
图5 闸门流量-开度SVM模型
3 试验仿真结果分析
先以柏条河闸门开度信息为例,其中143组数据作为训练数据,29组作为校验集,28组作为测试集,且各样本随机组合产生。柏条河闸门部分历史数据见表1。柏条河闸孔数为3,由试验可得,若用神经网络模型作为预测模型,3层神经网络结构为:输入层神经元个数为3,隐含层神经元个数为6,输出层神经元个数为3,并且隐含层激励函数为logsig,输出层激励函数为pureline。以此所建立的模型的输出误差较小,且输出开度不为负数。
单一的对比无法说明模型好坏。将表1中随机抽取的28组测试集数据作为基于水力学模型的输入,得出预测闸门开度,将实际值和两种模型的预测值置于同一图中,横轴为样本序号,纵轴为开度值。由此可见3种情况下的闸门开度有如下规律:闸孔2(中孔)开度较大,其次是靠近河岸的。从表1来看,在实际操作中大多数动闸不符合上文所述动闸规则,而且柏条河闸门流量会受到蒲阳河动闸的影响。而水力学模型建模时比较依赖上次动闸参数以及动闸规则,可知水力学建模时误差较大(见表2与图6)。神经网络建模3个闸孔的均方误差分别为12%、18%、5.0%,总均方误差为14.0%,低于实际工程要求的20%,可见神经网络建模较为理想。
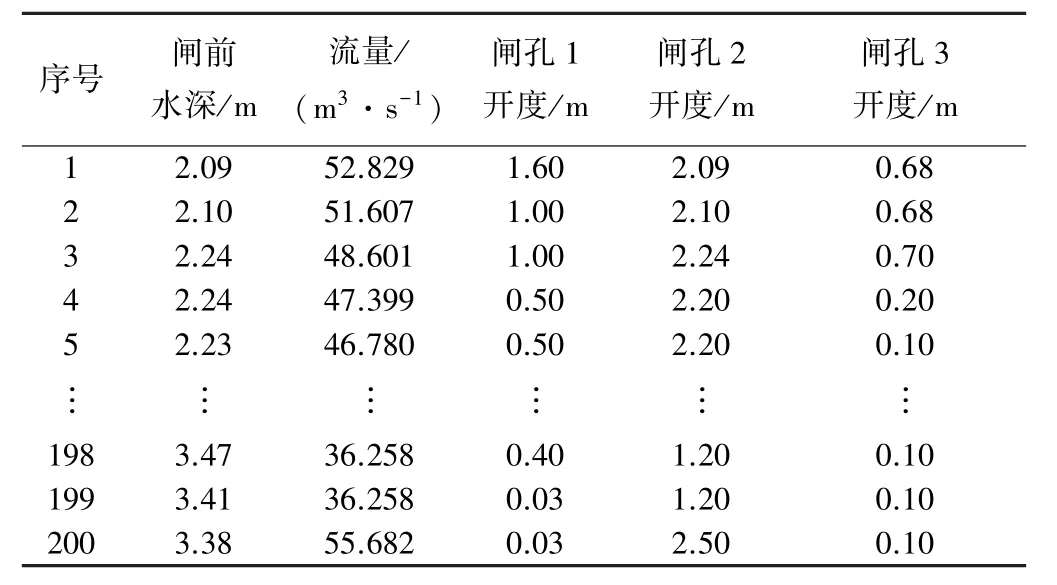
表1 柏条河闸门历史数据
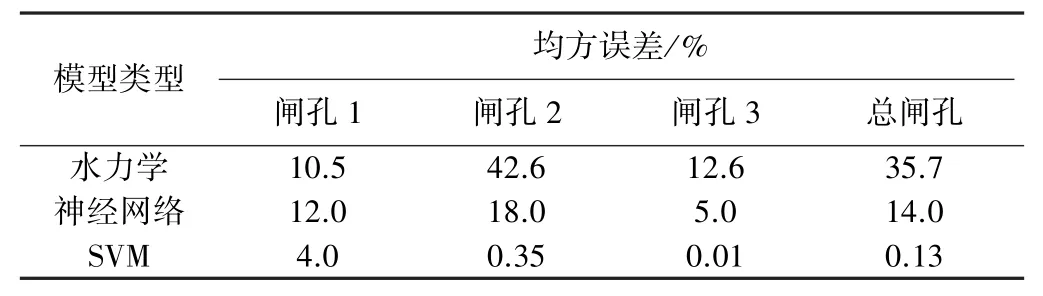
表2 SVM模型与其他模型预测结果均方误差比较
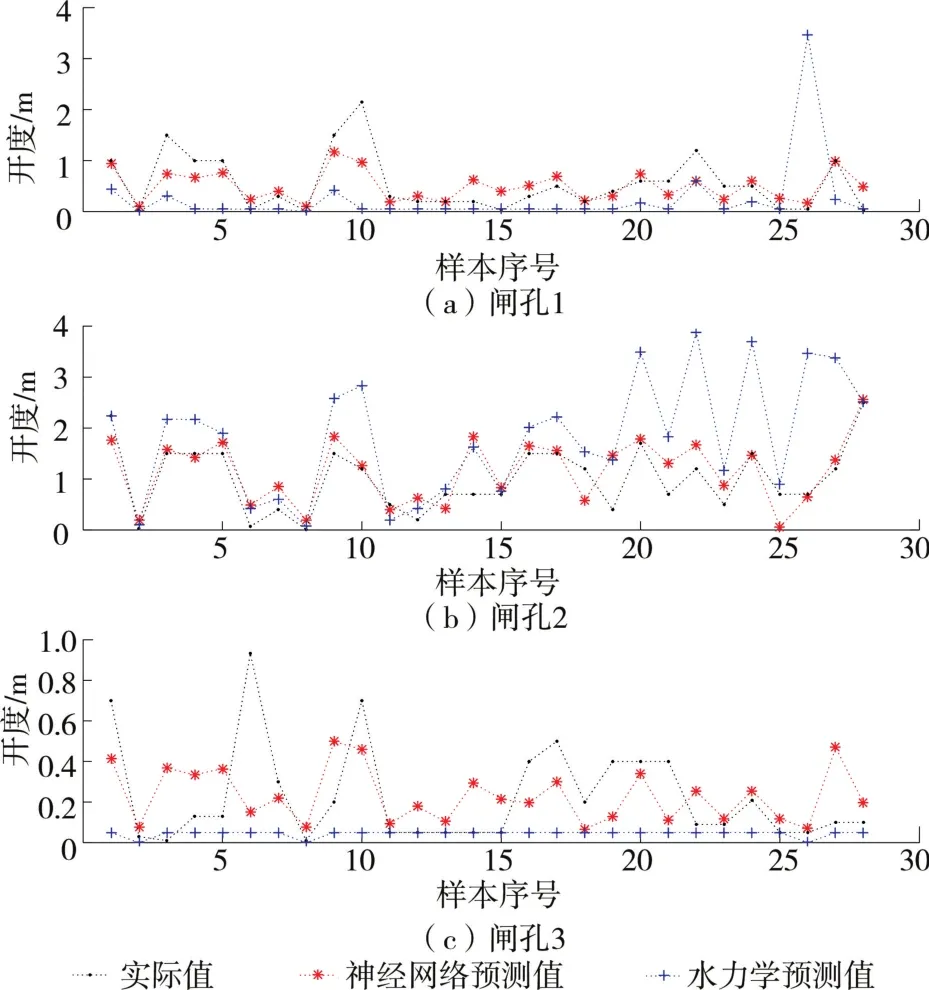
图6 神经网络模型和水力学模型输出各个闸门开度对比
由图7与表2可以看出,SVM单孔预测均方误差分别为4.0%、0.35%、0.01%,总均方误差为0.13%,对于动闸次数较多的闸孔2预测效果优于神经网路的预测效果,闸孔1与闸孔2也更接近实际值。从总闸孔误差和单孔误差来看,SVM模型的学习算法相对其他两种算法均较好。
分别从蒲阳河、走马河、江安河选取一组符合动闸规则且较为完整的闸门信息,用3种模型进行预测,结果见表3。由试验结果可以看出,满足动闸规则、河道等参数信息较为完整的情况下,水力学模型建模较为理想。对于蒲阳河数据,总体分布不均匀,导致神经网络预测结果误差较大,而SVM在3组数据中均有很好的预测结果。
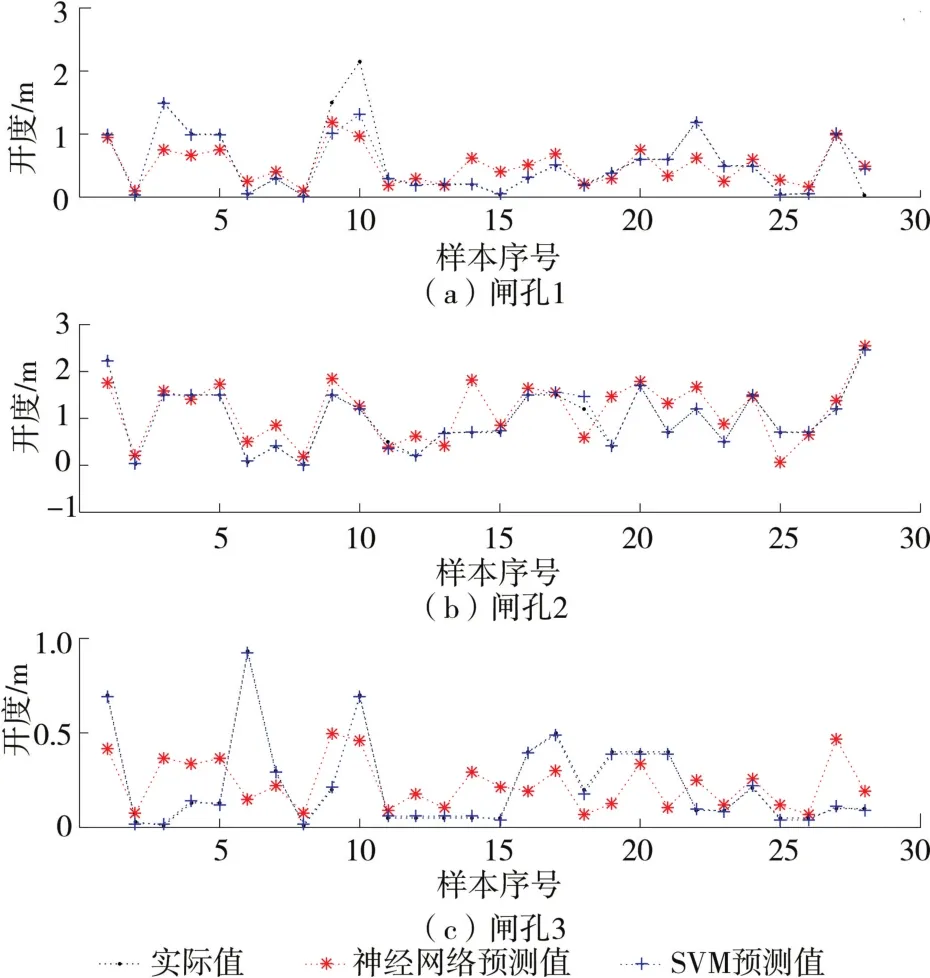
图7 神经网络模型和SVM模型输出各个闸门开度对比
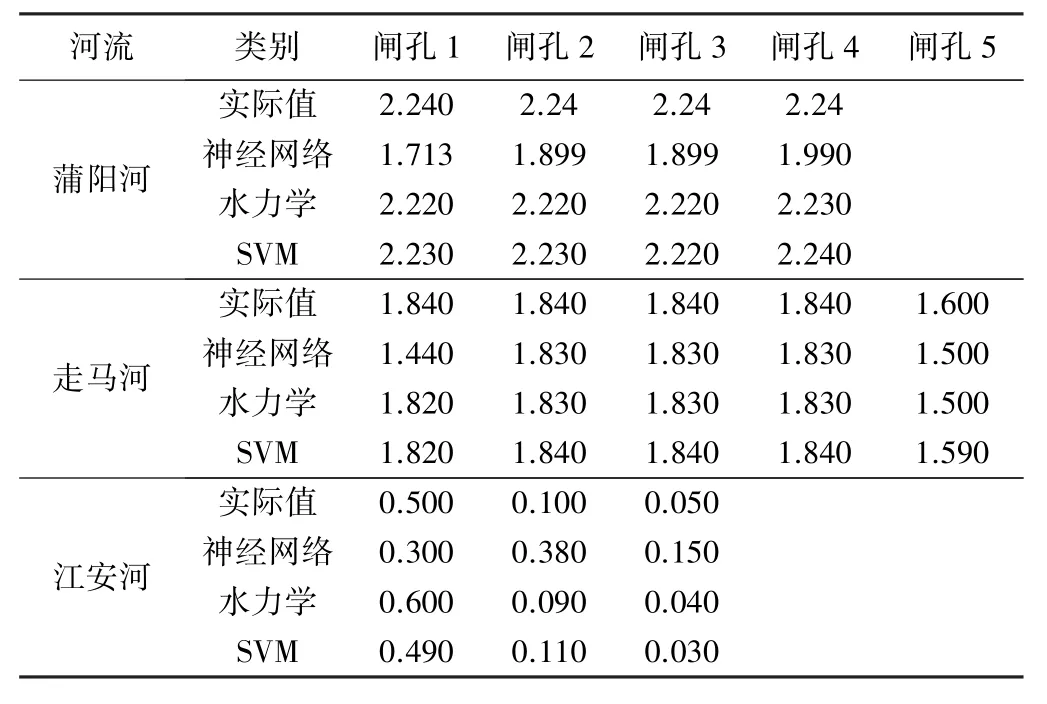
表3 蒲阳河、走马河、江安河实际闸门开度与各模型输出闸门开度对比 m
4 结 语
由仿真试验结果可以看出,基于水力学关系与机器学习构建模型各有优缺点。理论上的水力学建模比较依赖于河道信息、水位、动闸规则等,在实际工作中往往不能获取满足理论要求的数据。除此之外,水力学建模效果还受河道调度情况的影响。相对而言,机器学习建模比较依赖于历史数据的分布,在数据分布较为均匀且数据量大的情况下,所得预测结果较为准确。当水力学模型所要求的数据不理想时,可以选择机器学习模型建立预测模型。
在上文讨论中,使用不同的机器学习模型建模,建模效果也有明显差别。神经网络模型依赖数据量与数据的分布,而且模型在训练时易陷于局部最优,而SVM模型在数据量较少的情况下也能有较好的学习效果。对于都江堰灌区,受现场条件限制,加上对异常数据进行剔除修改,只能得到小样本数据集,用SVM建模较为理想。
——以淮阴闸为例

