动态时频谱分析、探测和跟踪的随机有限集法
王悦斌,蒋景飞,张建秋,*
1.复旦大学 智慧网络系统研究中心和电子工程系,上海 200433 2.电子信息控制重点实验室,成都 610036
非平稳信号的分析和参数估计,在雷达[1]、语音分析[2]和生物医学[3]等领域中正发挥着越来越重要的作用。然而,传统的谱估计算法只能分析出全局谱,无法揭示信号频率的局部变化。为了获取不同时刻信号分量的存在与否,以及各频率成分随时间变化情况,时频分布(Time-Frequency Distribution,TFD)的分析方法应运而生。其中短时 傅 里 叶 变 换 (Short-Time Fourier Transform,STFT)、Wigner-Ville分布和S 变换[4]是3种典型的时频分析算法。这些方法简单易懂,不需要额外的参数模型,应用十分方便。
可是,对多分量非稳态信号来说,这些传统算法在频率分辨率,非线性调频特性,以及动态时频谱(据文献[5]的定义:若时频谱中的信号分量随着时间动态地出现和/或消失,则称其为“动态时频谱”)的分析等方面还存在局限性。例如,Wigner-Ville分布对于单分量信号具有较好的时频分析能力,而对于多分量信号来说,则会引入较强的交叉项[6];S变换虽然具有可变的时频分辨率,但由于窗宽度是频率的函数,因而在不同的信号分析中,会表现出不同的能量集中度,从而限制了应用范围[7]。
为了提高对非平稳信号的时频表示(Time-Frequency Representations,TFRs)能力,近年来,人们研究出了许多新的算法。其中,广义S变换(Generalized S-Transform,GST)[8]通过多参数的窗函数,为克服时频分析方法所存在时频分辨率单一的缺点提供了一条新途径。然而,由于依赖于窗函数的选择,GST无法与不同类型的信号相适应。不同于GST,文献[9]提出的自适应 的 STFT (Adaptive Short-Time Fourier Transform,ASTFT)算法,可自适应非平稳信号特性,即据信号调频斜率的变化来不断调节自身STFT窗的长度。可是,对于具有多个分量且调频特性较复杂的时频信号,该算法不能获得较为可靠的调频斜率变化信息。匹配解调变换(Matching Demodulation Transform,MDT)[10]可以获得较高的瞬时频率估计精度,并且能有效提高时频表示的能量集中度,但该算法需要预先给定信号的全局参数模型,而大多数情况下瞬时频率的模型是未知的,因此该算法实用性较低。文献[11]提出了不需要信号全局参数模型的变分非线性调频模式分解(Variational Nonlinear Chirp Mode Decomposition,VNCMD)算法。该算法对于非线性调频信号的时频分析,在具有较好性能的同时,也具有较高的时频分辨率,并且可以解决信号频率分量交叉问题。然而,该算法需要预知信号分量数目,因而难以解决动态出现和消失多分量时频信号的分析问题。为解决这一问题,文献[12]提出一种基于Capon谱估计的多分量信号检测和追踪算法。该算法首先利用Capon谱估计得到时频谱的粗估计,进而估计出噪声谱,再进行信号峰值检测,最后进行匹配追踪,获得了去噪效果较好的时频分析结果。然而,该算法需要依靠全局谱判断信号分量的存在与否,因而实时性较差。最近,文献[5]提出一种利用狄利克雷混合模型来描述和估计动态时频谱的算法,进而给出了一种基于自适应狄利克雷混合模型的Rao-Blackwellised粒子滤波(Adaptive Dirichlet Process Mixture Model-based Rao-Blackwellised Particle Filter,ADPM-RBPF)算法。该算法实时性较好,提高了低信噪比下的时频谱估计的精度。可是,由于该算法利用STFT得到的原始时频谱作为观测,时频分辨率较差。
针对动态出现和消失多分量非平稳信号,本文提出了一种基于随机有限集的时频分析法。该算法利用时频变换在每个时刻获得的信号分量幅度的局部极值为测量的随机有限集,然后将时频信号各分量幅度和频率的变化描述为多项式预测模型[13],进而为每个信号分量建立起了一种新的线性高斯状态空间模型。这样,本文就将动态出现和消失的时频谱分析、探测和跟踪问题,归纳为可利用随机有限集进行多目标追踪的问题。借助于高斯混合概率假设密度(Gaussian Mixture Probability Hypothesis Density,GM-PHD)滤波器[14],本文算法可以分析动态的时频谱。对于GM-PHD滤波器,初始权重的赋值和权重的更新尤为关键。据时频分布的特点,本文提出了一种初始权重赋值算法,结合提出的谱分量幅度和频率的联合似然函数,进而解决了权重的更新问题。分析和数值仿真结果均证明:所提算法可有效提升动态时频谱的跟踪精度,对微弱时频谱分量的探测能力,以及对载频差异的分析能力。
1 时频分析的随机有限集模型
对于一个由多个调频调幅分量构成的时频信号,为了描述其分量随时间动态出现和消失的情况,采用Kn来表示随离散时间n变化的信号分量数目,这样本文考虑的时频信号的离散形式可描述为[5,12]
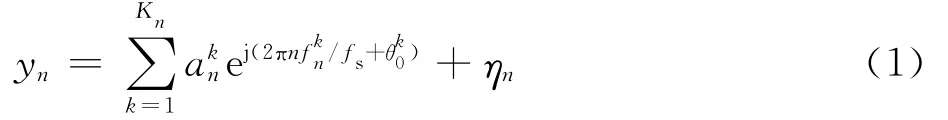
式中:yn为信号的观测值;akn和fkn分别为第k个分量信号的幅度和频率函数;θk0为第k个分量信号的初始相位;fs为采样频率;ηn为观测噪声。对时频信号式(1)进行STFT时频变换,可以得到信号的时频分布为[15]
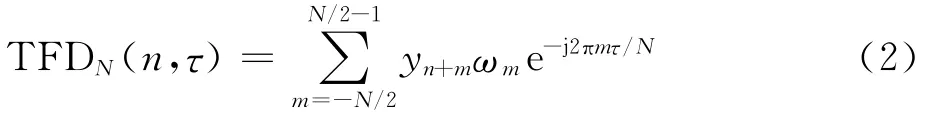
式中:n和τ分别为离散的时间和频率;N 为STFT短时窗的长度;ωm为窗函数。由于时频分布TFDN(n,τ)反映的是信号在(n,τ)时频邻域内的能量,那么任意时刻信号分量的能量,就必定会集中在该时刻的瞬时频率(Instantaneous Frequency,IF)附近。如果视每一时刻时频分布TFDN(n,τ)的局部极大值即式(3)中的Zn为测量值,这意味着任意时刻的信号分量必定包含在该时刻的Zn中。这是因为任意时刻时频分布TFDN(n,τ)的能量是信号能量和噪声能量的叠加,对高斯白噪声而言,其理想时频分布的能量是某一常数,这样当一个常数加上任一小的信号能量时,都将为高斯白噪声的理想时频分布能量增加一个局部极值。
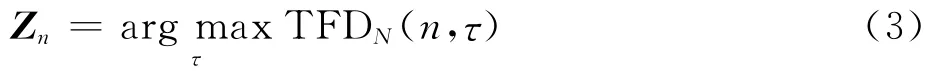
考虑到微弱信号分量的幅值可能很小,而观测噪声可能是非高斯的,以及高斯观测噪声的样本可能不是足够大,因此本文将所有检测到的局部极值均视为测量,如图1所示。由于观测噪声的存在,以及时频信号的分量可能随机出现或消失,那么每一时刻的局部极值也将是随机的。这样,可把Zn视为一个测量随机有限集(RFS)集合[16-17]:
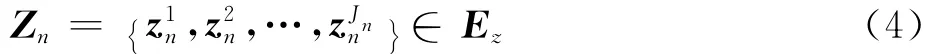
式中:Jn为n时刻局部极值(测量值)的个数;zjn=[]T为n时刻第j个局部极值幅度和频率的测量值集合,其中j=1,2,…,Jn;Ez为多分量时频信号的测量空间。因此,n时刻的测量随机集可以进一步表示为
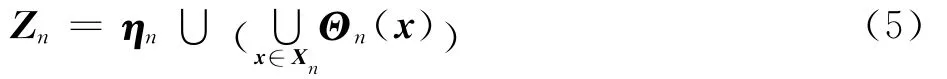
式中:ηn为n时刻源于观测噪声和/或杂波的测量RFS;Θn(x)为n时刻源于时频信号多分量状态x的测量RFS;∪为并运算。视信号分量为目标,则多分量信号的目标状态RFS就可描述为[16-17]

式中:Kn为n时刻目标个数(时频信号分量的个数);xkn为n时刻第k个目标的状态,其中k=1,2,…,Kn;Ex为多目标状态空间。n时刻的多目标状态随机集可以进一步表示为
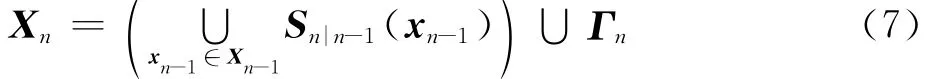
式中:Sn|n-1(xn-1)为n-1时刻的目标状态xn-1在n时刻的存活RFS;Γn为n时刻新生分量目标RFS。这样,可推导出基于RFS的全体多目标联合后验概率密度的贝叶斯递推公式[16-17]:


图1 峰值检测示意图Fig.1 Diagram of peak detection
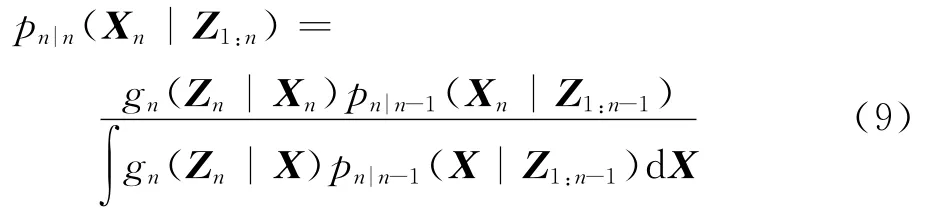
式中:Fn|n-1(·|·)为 多 目 标 转 移 概 率 密 度;gn(·|·)为多目标似然函数;Z1:n= {Z1,Z2,…,Zn}为前n 个时刻所有的测量 RFS;pn|n-1(·|Z1:n-1)为多目标预测概率密度;pn|n(·|Z1:n)为多目标联合后验概率密度。
式(8)和式(9)的递推公式需要在多目标状态空间上计算集积分,计算量非常大,在实际计算中一般难以实现。在线性高斯条件下,基于RFS的GM-PHD,通过把目标的概率假设密度(Probability Hypothesis Density,PHD)近似为混合高斯形式,可以得到递推形式式(8)和式(9)的闭合解[14]。针对式(4)和式(6)的 RFS变量,本文将为其提出一种新的线性高斯状态空间模型,使得本文可以利用GM-PHD滤波计算目标数量并估计各个目标的状态,进而得到了一种可分析动态出现和/或消失多分量时频信号的新复算法。
2 多分量时频信号分析
2.1 时频分量信号的状态空间模型
考虑到式(1)中信号分量的幅度akn和频率fkn,既可能是线性,也可能是非线性的,为了使讨论具有一般性,本文假设式(1)中的akn和fkn都是非线性函数,此时线性就可认为是非线性的特例。对于任一非线性函数,Weierstrass逼近定理[18]可知:任一有界闭区间上的连续函数都可以由该区间内的多项式以任意精度逼近。这意味着对任意连续函数,如果将其闭区间进行分割,且让每个分割出的小区间足够小,以致在每一小区间内,该函数都可以用一个低阶多项式(例如一阶多项式)以任一精度逼近。据这个原理,假设信号分量的瞬时频率fkn,在每一分割的小区间内可由L阶多项式描述:

式中:p(l)为多项式的系数。如果想用前M个时刻的频率值来预测当前时刻的频率,即

显然,式(11)是以h(m)(m=1,2,…,M)为系数的有限冲激响应(FIR)滤波器。将式(10)代入式(11),消去多项式系数p(l),可得

由式(12)无法唯一确定系数h(m)。考虑到信号的观测通常都是存在噪声的,这样就需要滤波器的噪声增益:

具有最小值。在式(12)的约束条件下,利用拉格朗日法就可求得式(13)的最优解为[13]:
1)当L=1时

2)当L=2时
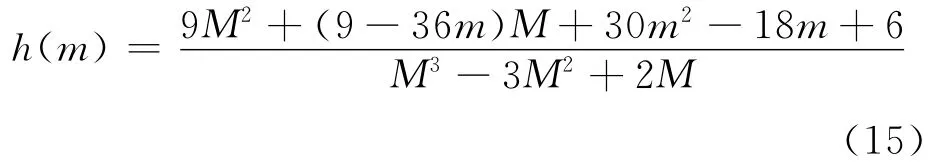
式中:m=1,2,…,M,其中M 表示滤波器的长度。当L为其他值时,计算结果详见文献[13]。
上面的分析表明:多项式预测模型式(11)与FIR预测滤波器在数学上严格等效。据上述多项式的预测模型,就可对时频信号分量的瞬时幅度和频率函数进行建模。定义第k个时频信号分量在n时刻的状态向量为


式(17)也可视作零阶多项式的预测模型,即用前一时刻的幅度值来预测当前时刻的幅度值。根据式(11)和式(17)的模型描述,式(16)的状态方程就可以表示为


有了式(18)幅度和频率的联合状态方程后,还需要建立信号分量幅度和频率作为联合参数的测量方程。假设第k个信号分量的测量为zn=[za,n,zf,n]T,其中za,n和zf,n分别为幅度和频率的测量值,则式(16)的测量方程可以表示为

式中:σn以0均值的加性噪声来描述式(3)的不确定性,噪声方差为R,观测矩阵为H =
在式(18)和式(20)所描述多分量时频信号的分析中,必须确定式(20)的测量zn属于式(1)中哪一个信号分量或杂波,才能根据式(18)和式(20)的状态空间模型进行时频分析,2.2节将讨论。
2.2 GM-PHD滤波的时频分析法
通过时频变换,本文将非线性观测方程式(1)转换成了式(20)的线性观测方程,而2.1节对线性/非线性调频函数,通过多项式预测方法,则将其变换成了线性的状态方程式(18)。这样式(18)和式(20)构成的时频分析状态空间模型是线性的。此外,由于本文假设噪声是高斯的,因此采用了GM-PHD滤波器。当式(1)观测噪声是非高斯时,则可以采用SMC-PHD[20]等滤波器,但建立的时频分析状态空间模型式(18)和式(20)有效,且将简化SMC-PHD等滤波器的计算复杂度。
2.2.1 算法预测
假设n-1时刻时频分量的后验概率密度是高斯混合形式[14]
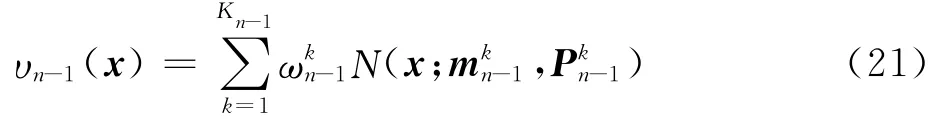
式中:Kn-1为n-1时刻的时频分量个数;和分别为分量k在n-1时刻的状态均值和方差;为分量k的权重(表示该分量为真实分量的概率);Ν(x;a,b)为随机矢量x服从均值为a、方差为b的正态分布。n时刻已存在分量的预测概率密度υS,n|n-1(x)为

式中:pS,n为时频分量存活下来的概率[14],分量k的预测均值和预测方差可通过 Kalman预测得到。注意,n-1时刻不属于任何时频分量的测量值将被假设为n时刻的新生时频分量。假设时频分量的预测概率密度也是高斯混合形式:
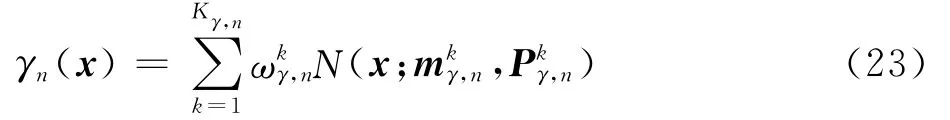
式中:Kγ,n为n时刻假设时频分量的个数。假设时频分量k的初始权重ωkγ,n的赋值方式需要据应用场景来确定。在时频分析中,考虑到测量值的瞬时幅度越大,其属于真实时频分量的概率就越大,而在信噪比高的环境下,杂波较少,那么测量值来自于真实时频分量的概率也越大。综合上述两个因素,本文给出权重ωkγ,n的初始值为
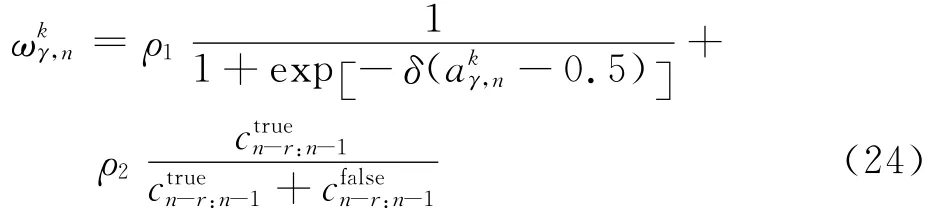
2.2.2 算法更新
获得式(1)的观测后,对N 个观测值进行时频变换,例如STFT,时频变换后的结果通过式(3)获得n时刻测量值后,需要对权重进行相应的更新。对于每个测量,权重)根据贝叶斯公式更新为[14]
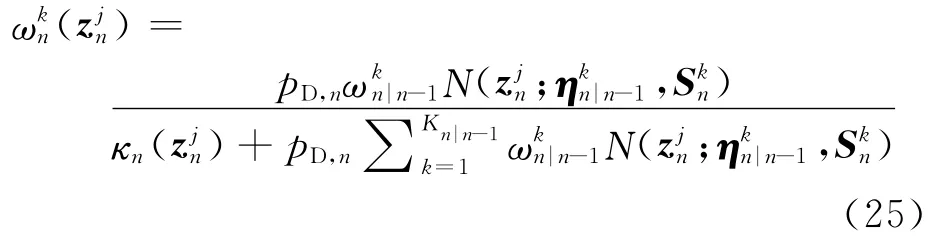
式中:pD,n为检测到时频分量的概率;)为杂波在上的概率密度,一般取常数1/V,其中V是测量空间的大小;分别为来自时频分量k测量的预测均值和方差;Kn|n-1=Kn-1+Kγ,n为n 时刻预测的时频分量个数。当假设时频分量的频率和幅度相互独立时,式(25)中的似然函数可以写为
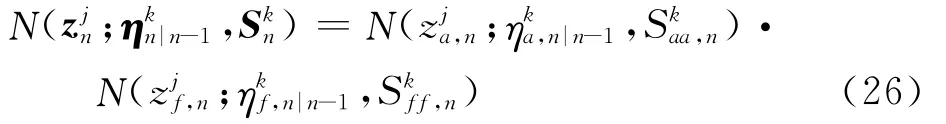
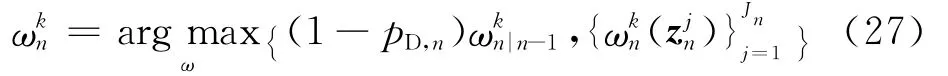
事实上,测量zjn只可能来自某一个时频分量或者来自杂波。这样,为了降低计算复杂度,本文根据权重的大小将测量与时频分量进行关联式(27)表明:当n时刻所有时频分量的权重都更新后,其中没有与目标关联过的测量值,将假设为下一时刻的新生时频分量。然而由于杂波的存在,必须要有一个判别准则来决定假设时频分量是否来自真实的新时频分量,还是来自杂波。由于杂波能量较为分散,而时频分量的能量相对较集中,而据式(25)可知,真实时频分量的权重将接近于1,而虚假时频分量(杂波)的更新权重将接近于0,应该舍去。这样本文的判别准则如下:
1)若ωkn>0.5,该假设分量为真实分量。
2)若ωkn>1/V,该分量为假设分量。
3)否则,该假设分量为杂波(该准则也同样适用于判断时频分量的消失)。
3 时频分析的多目标追踪算法
步骤1 对存在的时频分量k进行Kalman预测,其中k=1,2,…,Kn-1。
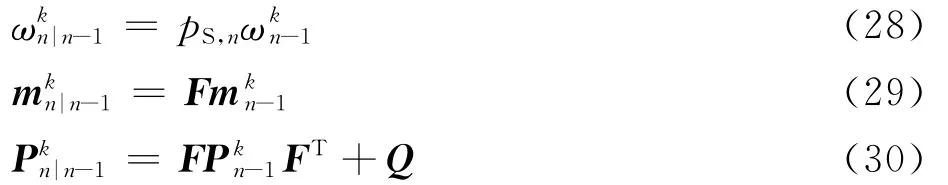
式中:Q为过程噪声协方差矩阵。
步骤2 由式(27)可知,对在n-1时刻判别为来自杂波的Kγ,n个测量视为n时刻的假设时频分量,并据式(24)赋予相应的初始权重。
步骤3 对存在时频分量或假设时频分量k的测量进行预测,其中k=1,2,…,Kn-1+ Kγ,n-1。

式中:R为测量噪声方差。
步骤4 对于给定的zjn,其中j=1,2,…,Jn,式(27)将该测量值与时频分量相关联,并获得该分量权重的更新值;更新时频分量的状态方差。
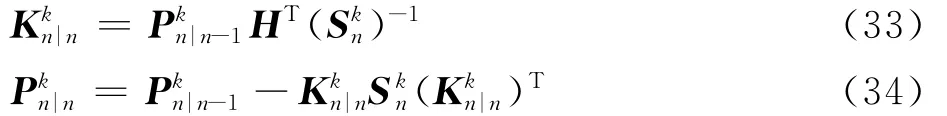
1)若该测量由某一时频分量k产生,更新该时频分量的状态均值mkn|n
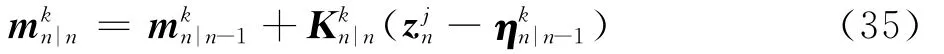

步骤5 根据判别准则,删除权重较小的分量,接受权重较大的假设时频分量为真实分量。
4 仿真实验
为了使仿真实验更具说服力,本文采用了文献[5,12]的仿真实验思路来设计动态时频谱。仿真实验分为3部分:① 仿真中的多分量线性调频信号来自文献[5];② 仿真中包含微弱信号和非线性调频信号的情况参考文献[12];③ 主要考虑载频差异较小信号的时频分析,以借此来说明所提算法的高分辨率性能。
4.1 多分量线性调频信号
第1组仿真信号包含10个线性调频分量,形式为
式中:αk和βk分别为第k个信号分量的初始频率和调频斜率;Ik(t)为第k个信号分量是否存在的指示函数,其形式为
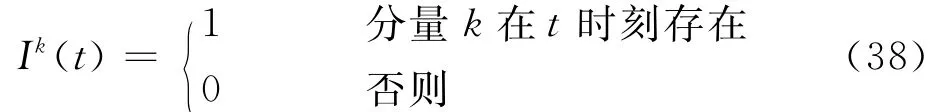
加性复高斯白噪声η(t)的方差为σ2η,信噪比(SNR)定义为[21]

仿真信号长度为100s,采样频率为512Hz,信噪比为-8dB。图2分别给出了信号进行STFT、Capon 变 换[12]和迭 代 自 适 应 (Iterative Adaptive Approach,IAA)谱估计(见附录 A)的时频分布图,其中STFT、Capon和IAA均采用矩形窗,窗长N=128,窗的移动步长为N。对于图2的含噪时频图,分别采用ADPM-RBPF算法[5]、基于 Capon的峰值检测法[12]和本文算法进行分析。本文算法中状态空间模型参数为L=2,M =3,σa=10-2,σfm=10-4,其中m=1,2,3。时频分量存活下来的概率pS,n=0.9,时频分量被检测到的概率pD,n=0.9,S型曲线的陡峭程度参数δ=20,权重因子ρ1=2ρ2。
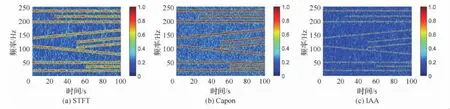
图2 线性调频信号时频图Fig.2 Time-frequency spectra of chirp signal
从图3(a)可以看到,在低信噪比下,ADPMRBPF算法不能很好地去除杂波;从图3(b)可以看到,基于Capon的峰值检测法可以更好地去除杂波,但是该算法必须依靠更多的谱来判断真实的信号分量和杂波[12],因此实时性差。在相同的窗长下,本文算法的实时性与ADPM-RBPF相当,均优于基于Capon的峰值检测法。而图3(c)和图3(d)则表明:本文算法明显优于ADPM-RBPF算法,当短时谱是利用IAA估计得到时,本文算法效果最佳。
单时频分量背景下的均方根误差已不再适用于对本文算法的性能评价,因为需要考虑状态估计值和真实值之间的对应关系。为此,本文利用OSPA(Optimal SubPattern Assignment)距离[22]来评价多分量估计的误差。对于瞬时频率真实值珚F=[珚f1,珚f2,…,珚f珡K]和估计值^F=[^f1,^f2,…,^fK^],当珡K≤^K时,OSPA距离定义为[22]
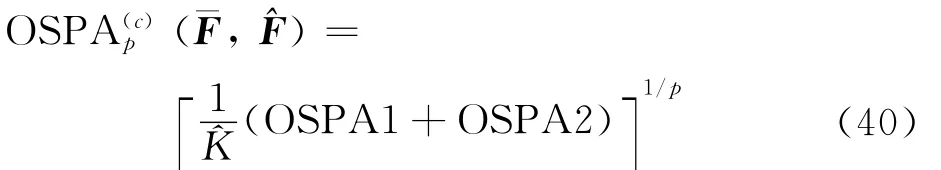
式中:

式中:参数c为目标状态估计误差的阈值,同时可调节集合势的估计误差比重。本文采用p=2阶,c=0.1的评价指标。
图4给出了3种算法时频谱估计的平均OSPA曲线,每种算法均进行100次蒙特卡罗仿真。通过图4可以看到,本文算法瞬时频率的估计精度优于ADPM-RBPF算法和基于Capon的峰值检测法,在低信噪比(SNR<-6dB)下,本文算法优势更加明显。这是因为本文算法为调频函数建立一个可靠的状态转移模型(18),这个新模型使得在低信噪比下,本文算法能依据该模型鲁棒地跟踪时频分量。需要强调的是,基于IAA短时谱的本文算法估计性能最佳,这是因为IAA算法优于STFT算法。
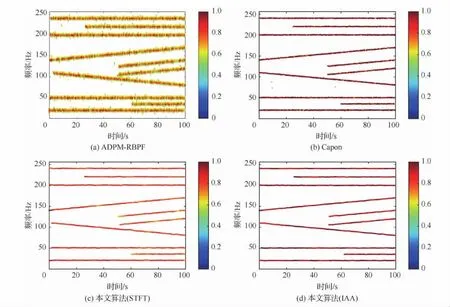
图3 线性调频信号的时频重构图Fig.3 Time-frequency reconstruction spectra of chirp signal
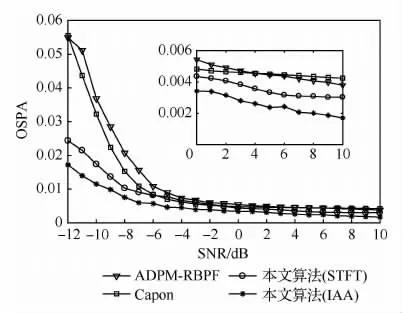
图4 IF估计误差Fig.4 IF estimation error
4.2 复杂多分量时频信号
实际中,信号分量幅度大小往往不同,调频方式多样。为了验证本文算法在各种复杂情况下的鲁棒性和有效性,本文将非线性调频特性、信号分量的动态出现和消失以及微弱信号分量都结合起来进行分析。第2组仿真信号形式为

仿真信号长度为100s,采样频率为512Hz,信噪比为0dB。图5给出了信号进行STFT变换、Capon变换和IAA谱估计的时频分布图。从图中可以看出,信号分量k=4较强,而信号分量k=3非常微弱,其局部信噪比相当于-10.46dB,检测难度变大。
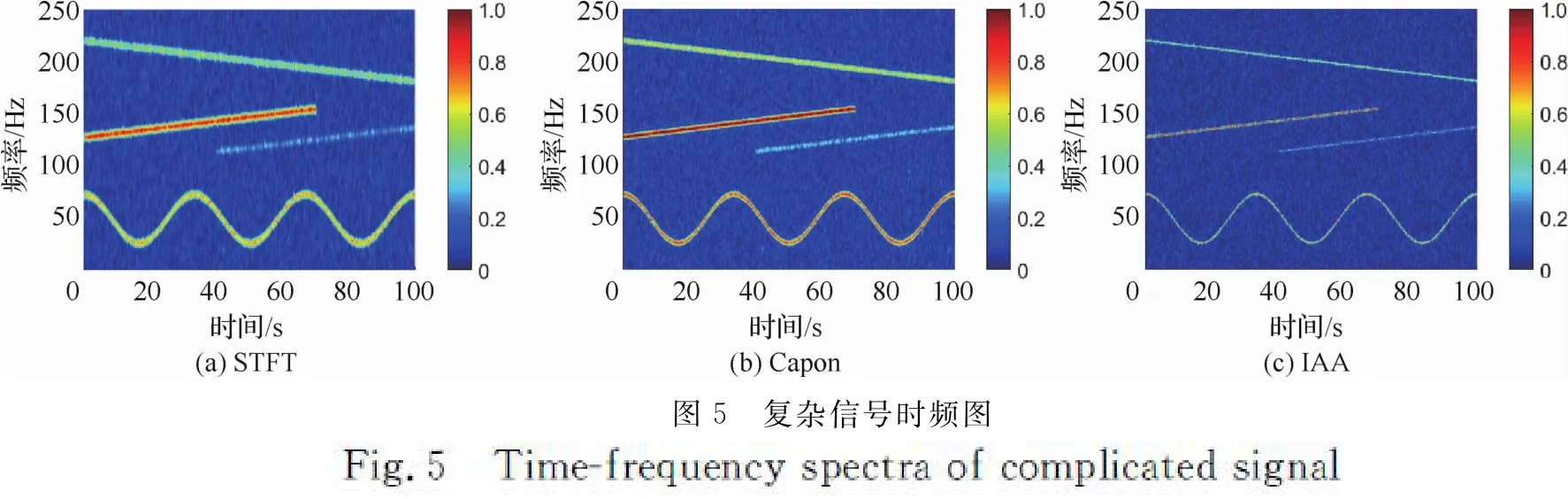
图6给出了本文算法与对比算法的时频重构图,可以发现,ADPM-RBPF算法(见图6(a))不能完整重构出信号分量k=3,这是因为该算法需根据功率谱大小来进行随机采样获得测量值,从而导致微弱信号分量被检测到概率很小。基于Capon的峰值检测法(见图6(b))在微弱信号以及调频斜率较大区域均出现漏检情况,这是因为该算法采用的假设检验在信号能量较低区域(低信噪比区域)漏报率高的缘故。本文算法则可利用建立的预测模型式(18)来预测非线性调频分量在下一个采样时刻可能的近似值,同时也考虑到了时频分量未被检测到的概率(见式(25)),因此不论基于STFT或IAA短时谱,均可以完整重构出全部4个信号分量。
图7给出了ADPM-RBPF算法、基于Capon的峰值检测法,以及本文算法估计出的信号分量数目,每种算法均进行100次蒙特卡罗仿真。当微弱信号分量存在时,ADPM-RBPF算法估计误差较大;而当调频斜率较大或微弱信号分量存在时,基于Capon的峰值检测法对于信号分量数目的估计误差较大。本文算法分析结果较为理想,这是因为本文算法考虑到了目标未被检测到的情况。
4.3 载频差异较小的时频信号
为了获得较高的时间分辨率,必须减小时间窗的长度。然而,对于载频差异较小且变化剧烈的时频信号,STFT很难同时满足时间和频率分辨率的要求,而IAA谱估计算法具有高时频分辨率和鲁棒性,因而适合载频差异较小的时频分析问题。第3组仿真中,时频信号包含2组载频差异较小的线性和非线性调频信号为
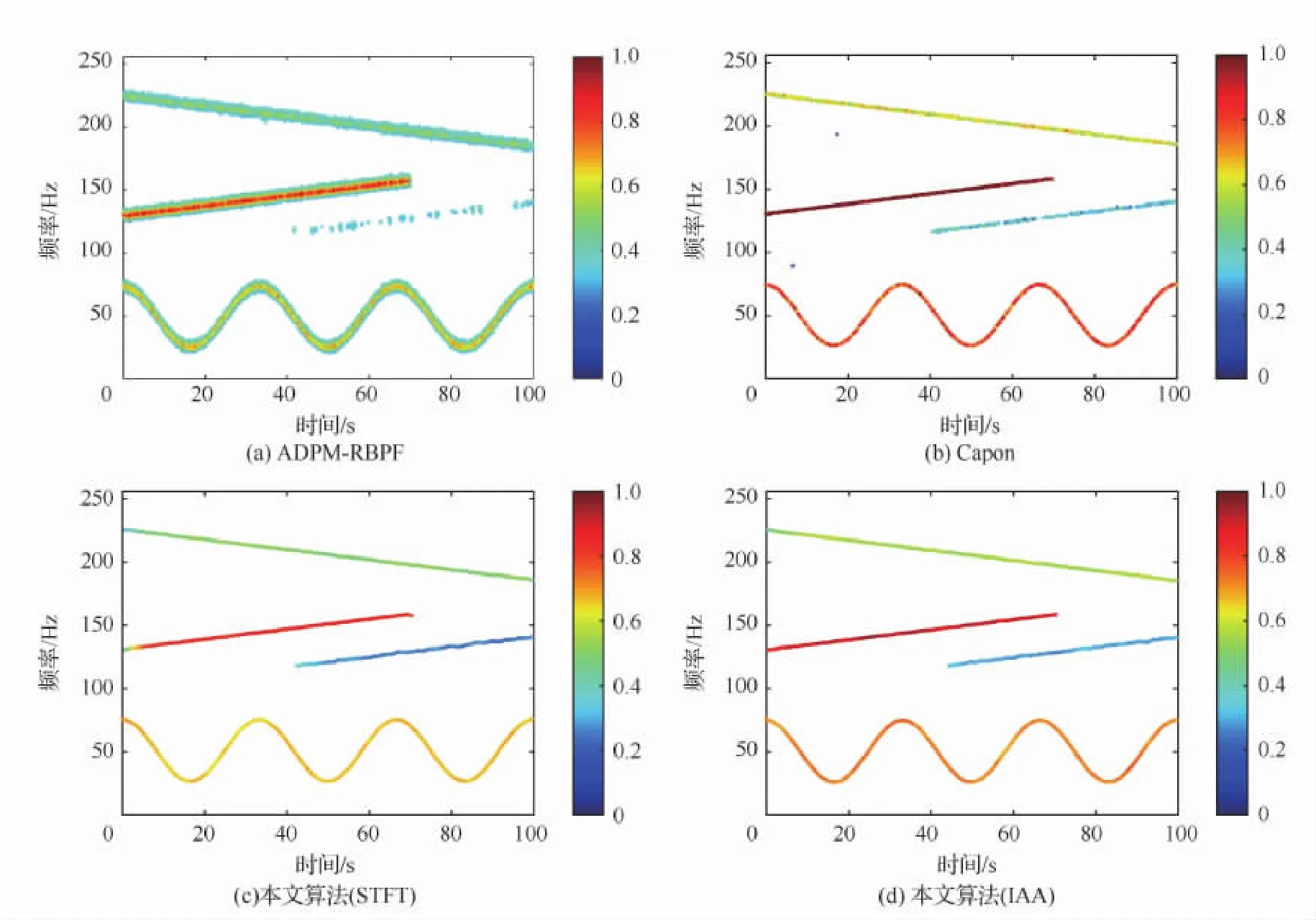
图6 复杂信号时频重构图Fig.6 Time-frequency reconstruction spectra of complicated signal
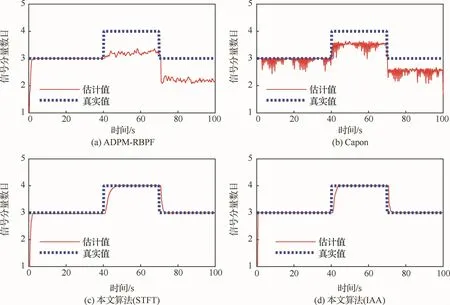
图7 复杂信号分量个数估计Fig.7 Components estimation of complicated signal
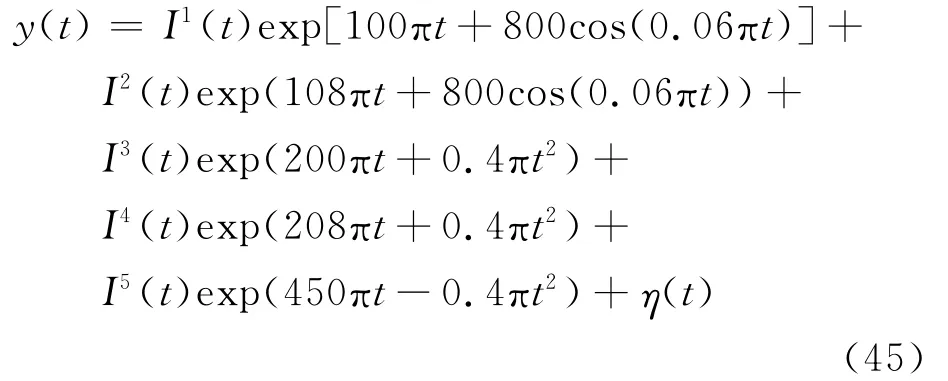
仿真信号最小载频差异约为0.008(归一化),信号长度为100s,采样频率为512Hz,信噪比为0dB。图8给出了信号进行STFT变换、Capon变换和IAA谱估计的时频分布图,3种算法均采用矩形窗,窗长N=128,窗的移动步长为N。可以看到,在信号载频差异较小的区域,STFT和Capon下信号分量均存在严重的重叠。
从图9(a)~图9(c)中可以看出,当信号分量间载频差异较小时,ADPM-RBPF算法、基于Capon的峰值检测法以及基于STFT的本文算法均无法分析出两个载频差异较小的信号分量。相反,如图9(d)所示,基于IAA时频谱的本文方法即使在载频差异较小区域也可获得较为理想的分析结果。图10给出了每种算法都进行100次蒙特卡罗仿真的信号分量数目的估计结果。可以看到,只有基于IAA时频谱的本文算法具有较为理想的估计效果。
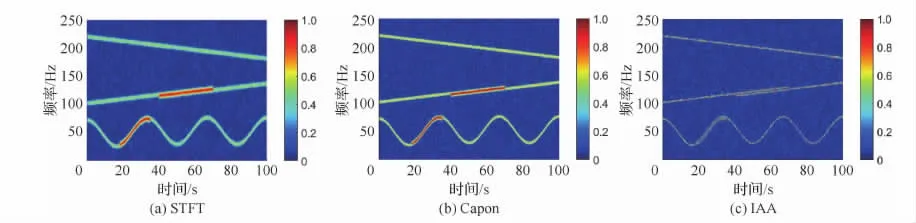
图8 载频差异较小信号时频图Fig.8 Time-frequency spectra in close modes
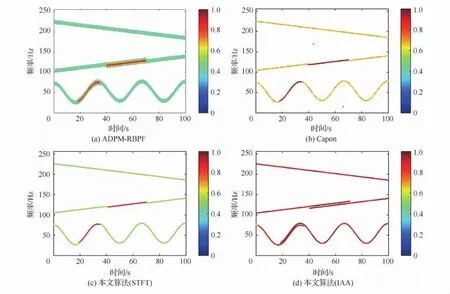
图9 载频差异较小信号时频重构图Fig.9Time-frequency reconstructionspectrainclosemodes

图10 载频差异较小信号分量个数估计Fig.10 Components estimation of signal in close modes
5 结 论
针对由多个信号分量构成的时频信号且其分量动态出现和消失的时频谱分析问题,本文提出了一种分析、探测和跟踪动态时频谱的随机有限集法。
1)该算法首先将观测到的信号进行时频变换,进而视每个时刻的时频谱幅度的局部极值为测量。分析表明:每个时刻测量的集合是一个随机有限集。
2)基于提出的状态和测量随机有限集模型,本文给出了利用高斯混合概率假设密度滤波器,并结合多项式预测模型以及提出的初始权重赋值算法,来进行动态时频谱的分析、探测和跟踪的算法。
3)仿真结果均证明:所提算法在分析精确度、鲁棒性、对微弱时频谱分量的探测能力、以及对载频差异的分析能力等诸方面均优于文献中报道的算法。

式中:y=为时间窗内的测量数据,N为时间窗的宽度;I为离散化频率 格 点 的 个 数;为离散化频点τ对应的频率矢量,tn为采样时刻;eτ为离散化频点τ对应的幅值;ε为均值为0且与信号相互独立的高斯白噪声。
对式(A1)所描述的信号模型,IAA算法的时频谱估计结果为
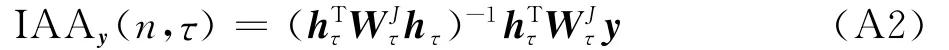
式中:IAAy(n,τ)为n时刻IAA算法估计得到的谱;WJτ为第J次迭代中针对频点τ的加权矩阵。IAA算法采用迭代技术,即每次迭代开始时都利用了上一次谱估计结果来构建加权矩阵
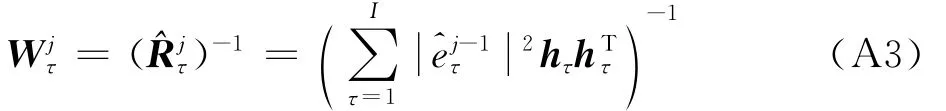
式中:为第j次迭代中针对频点τ的加权矩阵;为第j次迭代开始时针对频点τ估计的信号 协方 差 矩 阵 ;为 第j-1次 迭 代 的 谱估计结果,其中初始谱估计结果由周期图法获得[23]。

