面向时间协同的多无人机队形变换最优效率模型
顾伟,汤俊,白亮,老松杨
国防科技大学 系统工程学院,长沙 410073
在战场使用中,无人机通常需要根据任务要求集结成具有一定形状的编队;在执行任务期间则要保持一定的编队形状,从而提高任务完成能力;而当战场环境发生变化时,无人机编队则必须进行编队重构,才能保证编队的生存能力。无人机编队是由具有自主控制能力的多架无人机按照指定的队形位置排列形成的一个较大规模的无人机集群。在一定的控制器作用下,不仅能使编队中所有的无人机在飞行过程中保持队形的稳定,协同完成各项任务,而且可以进行队形的实时调整[1-2]。
相对于单无人机,多无人机构成的编队具有更大的优势[3]。在目标侦查时,由多架无人机同时从多个角度进行探测可以获取目标的多维立体信息[4];在战场打击中,多架无人机协同配合进行饱和式的全方位打击,可以有效增强杀伤能力,进一步提高目标毁伤概率[5];另外,通过合理的队形编排,可以使编队中的无人机更好利用其他成员产生的上升气流,提高气动效率、减小能源消耗,进而增强无人机编队的续航能力[6]。
对于无人机编队队形变换的航迹规划,许多研究人员把无人机的队形变换过程抽象成一个最优化问题,优化目标是整个过程的持续时间和能源消耗函数,需要考虑的约束条件包括无人机自身的性能约束以及无人机与其他成员之间的碰撞约束[7]。华思亮等[8]通过分析无人机编队队形变换任务的耦合特性、碰撞避免以及编队拓扑动态变化等问题,提出了编队队形变换问题的数学模型,并利用模型预测控制算法进行求解。熊伟等[9]利用控制作用参数化以及时间离散化,将无人机编队队形变换的时间最优问题转化为一种带自由末端状态约束的离散型优化问题,并采用改进的遗传算法进行解算,取得了较好性能。王祝等[10]利用离散化和凸近似方法将无人机航迹规划问题转化为凸优化问题,并基于罚函数序列凸规划进行求解。Ajorlou等[11-12]建立了基于人工势场的编队控制系统。
另外还有概率法、图论法、各类智能优化法等等,但是以上这些航迹规划方法大部分都是给定队形变换的起点和终点,通过赋予一定的任务要求或者在起点和终点间设置障碍,然后求解一条从起点到终点的最优路径。但是实际中有些情况仅需要多架无人机集合成某一队形待命,这时候队形变换的终点位置是未知的。显然,选择不同的终点位置,其队形变换的效率是不同的。另外,多无人机路径规划效率的评价标准比较复杂,单无人机路径规划可以将路径最短、安全无碰撞作为最优标准,但是对于多无人机而言,缩小某一单架无人机的路径长度必然会增加剩余无人机的飞行路径,在增加时间协同要求后,即要求同时到达后,其情况更为复杂。总体而言,在无人机编队的研究中,寻找连接确定起点和终点的最佳路线的方法很多,通过效率衡量方式,求解队形变换空间最优位置的方法相对较少。
本文将队形变换能源消耗与队形变换完成时间确定为效率衡量指标,提出无人机队形变换的最优效率模型。根据无人机编队在实际情况中可能遇到的几种具体的队形变换问题,基于编队集结、编队保持和编队重构等不同特点,给出了这些具体队形变换下的最优效率计算公式,从而获得队形变换的最优空间位置,最后进行了仿真实验验证。
1 队形变换问题描述
无人机的队形变换问题[13]主要是指一定数量的无人机根据变换要求移动位置,形成新的队形形状。如图1所示,无人机由矩形编队A1~A6变换到目标三角编队B1~B6。影响队形变换效率的因素包括两个:一个是队形变换的最终目标位置,另一个是变换时选择的路线。在目标位置确定时,选择不同的路线,其消耗是不同的。同样,当固定飞行方式时,如都为匀速直线运动,选择不同的目标终点,队形变换的效率也是不同的。因此选择合适的目标位置和变换路径对于快速、高效完成整个队形变换有着重要意义。本文主要是固定飞行方式,利用效率衡量指标,求取队形变换的最佳目标位置。队形变换中的最优效率包括能源消耗最小以及完成时间最短。
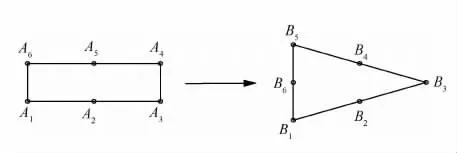
图1 队形变换Fig.1 Formation transformation
记编队中的各无人机为 UAVi(i=1,2,…,n),n为编队中无人机的数量,UAVi在队形变换前的位置为Ai,变换后的位置为Bi(Ai,Bi∈R3)。无人机UAVi从Ai移动到Bi走过的路程为si,所产生的能源消耗为wi,花费的时间为ti。则无人机编队在队形变换中的总能耗为
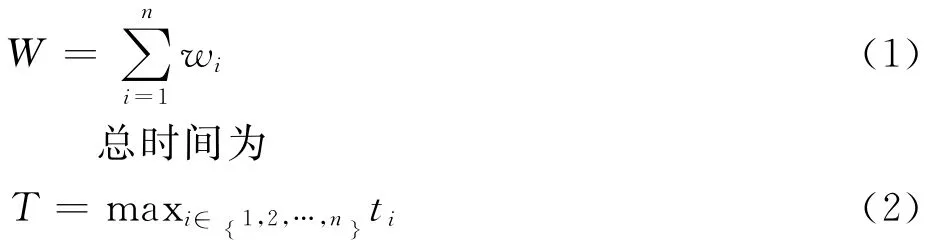
1.1 最小能耗变换
为了简化研究问题,假设所有无人机均进行匀速运动,不考虑转弯能耗以及外界环境的影响。显然,在无障碍环境中,只要目标队形的位置确定,无人机采取匀速直线运动,在无碰撞的情况下,一定是能耗最小、时间最短。如果是带始末状态约束的固定翼无人机,也存在唯一的Dubins最短航迹。当给定起点和目标点间的航迹能唯一确定时,最优效率模型的关键就是要在目标集结区域中寻找相应的能耗最小和时间最短的目标编队位置。
对于UAVi,由于存在时间协同约束,各无人机必须以相同的时间t到达指定位置,所以速度与路程呈正比,即

忽略空气密度、迎风面积等不同造成的影响,UAVi所受阻力fi与速度的平方呈正比:

式中:k为常系数。
忽略热效应等其他影响,为了克服空气阻力所产生的能耗为

由式(1)、式(3)~式(5),最小能耗模型可描述为

式中:c=k/t2,当t一定时,c为常数。
1.2 最短时间变换
最优效率的另一种评价标准是完成变换所需的时间最短。首先假设各无人机以相同的最大飞行速度vmax匀速运动,则时间ti与路程si呈正比:

再以T=maxi∈{1,2,…,n}ti作为总的协同时间,令无人机UAVi以vi=si/T的实际速度匀速运动。
由式(2)和式(7),最短时间模型可描述为

式中:a=1/vmax为常数。
1.3 能耗-时间综合变换
由式(6)和式(8)可以知道最小能耗与最短时间并不是一个正相关的关系,在追求最小能耗时得付出时间代价,同样在追求最短时间时也要付出更多的能耗代价。在实际情况中往往都是要求在规定时间内完成固定形状的编队集结。这就是一种典型的能耗-时间综合变换。
2 实际变换问题求解
2.1 队形描述
在实际中,无人机编队以平面队形居多,因此在这里主要求解无人机的平面队形变换问题。另外化为平面队形后,在以后出现可能的碰撞情况时,可以实行变高避撞。在平面队形研究中,三维空间位置变量Ai和Bi可简化为二维平面坐标,记 Ai= (xi,yi),Bi= (xi′,yi′)。对 平 面 队 形{Bi,i=1,2,…,n}进行如下变换描述:
1)寻找队形虚拟编队中心

2)计算Bi和Bmiddle之间的距离

经过变换后,无人机UAVi的位置可由Bmiddle、di和θi唯一确定:

利用虚拟编队中心法对队形进行变换描述,可以有效减小问题规模,而且随着无人机数量的增加,其效果越明显。
2.2 编队集结
编队集结中的队形变换主要是指一定数量的无人机按照要求形成固定队形。在固定队形中,di为已知量。根据不同的要求,θi可能为已知量,也可能是未知变量。例如:如果要求无人机按方向正北的三角攻击队形集结,θi就是已知量;如果只要求呈三角队形,那么θi就是变量。
假设各无人机均沿直线进行匀速运动,即

2.2.1 θi已知
为了便于求解,进行一些等价变换,最小能耗模型为
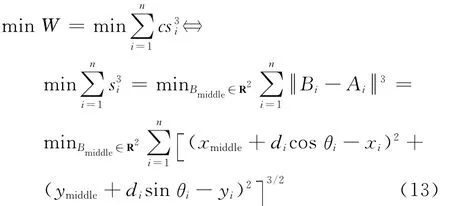
模型中只有xmiddle和ymiddle两个未知变量,利用最小二乘法求偏微分即可求解此类min问题。最短时间模型的具体计算模型为
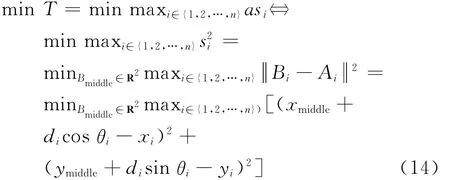
对于这类min-max问题不能直接求解,利用文献[14]的方法将问题转化为带权值的min问题,即引入权值ωi,式(14)可转化为
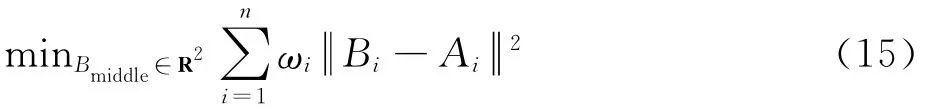
利用Lawson算法[15]进行权值迭代计算:
2)迭代ωi,ωm+1i=ωmiBi-Aipm,其中
3)判断ωi值,迭代终止条件为ωm+1i<ε,ε为既定的极小常数,其取值视对算法的精度及对实时性能要求而定。
计算出最小能耗变换位置和最短时间变换位置后,通过加权就可以进行能耗-时间综合变换。记最小能耗和最短时间目标队形的虚拟编队中心分别为

记最小能耗变换所用总时间为t1,最短时间变换所用时间为t2,t为实际的变换时间(t≥t2),则能耗-时间综合变换目标编队中心位置为

式中:t=f(α),α∈[0,1],且f(0)=t2,f(1)=t1。
2.2.2 θi未知
引入变量θ,令θi=θ+Δθi。其中Δθi为基准坐标下无人机UAVi与队形中心Bmiddle的夹角,只要队形形状固定,Δθi为定值。θ为队形绕中心点的旋转角度,是一个变量。将θi=θ+Δθi代入式(13)得θi未知时的最小能耗模型为
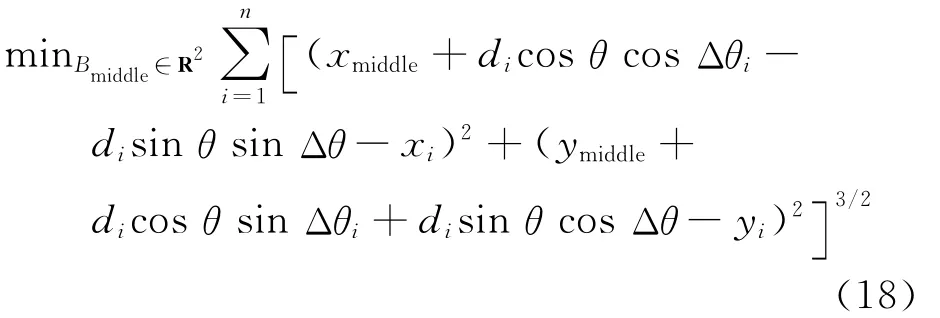
利用最小二乘法求偏微分可对式(18)进行求解。将θi=θ+Δθi代入式(14)得θi未知时的最短时间模型为
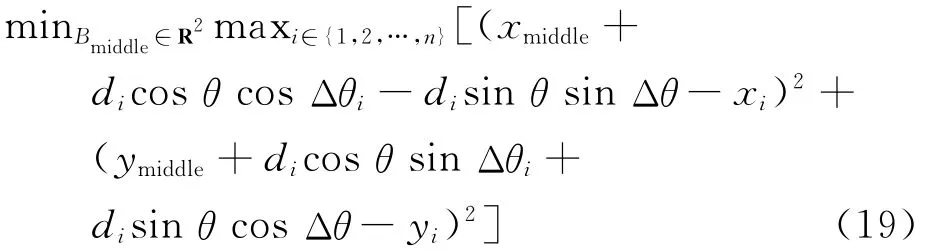
式(19)求解过程同2.2.1节,转化为 min问题后利用Lawson算法进行权值迭代计算。
当θi未知时,最小能耗目标编队位置可表示为 (xmiddle1,ymiddle1,θ1),最短时间目标编队位置可表示为 (xmiddle2,ymiddle2,θ2),则能耗-时间综合变换的目标编队位置为

2.3 编队保持
无人机编队在飞行过程中和执行任务期间通常需要维持一定的队形,通过平移和旋转可以使队形保持刚性。平移时,每架无人机的移动速度和移动距离均相等,即能耗和时间均相等;旋转时,选择不同的绕转点,每架无人机的移动速度和移动距离都是不同的,选择不同的绕转点,能耗和时间也会有所差别。因此选择合适的绕转点对于快速、高效地实现队形刚性旋转有着重要意义。
设Bq=(xq,yq)为绕转点,θ为旋转角度,则无人机UAVi移动的路程为
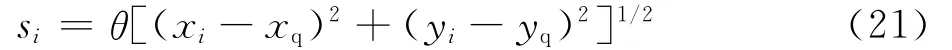
当指定旋转角度θ时,最小能耗模型为
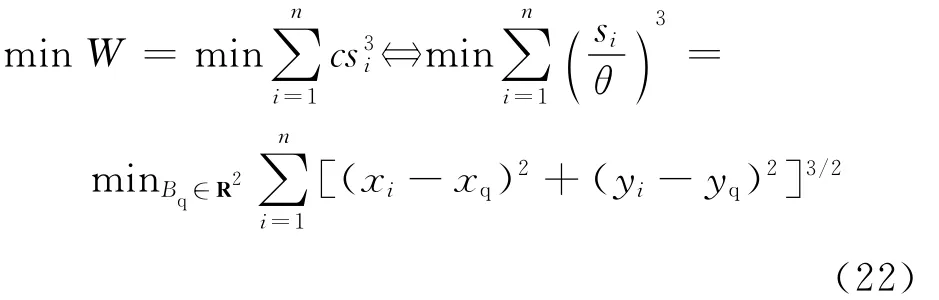
指定旋转角度θ时,最短时间模型为

求解方法同2.2.1节。能耗-时间综合旋转的目标绕转点可表示为
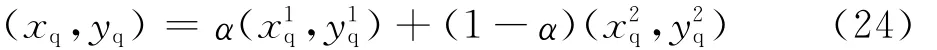
式中:(x1q,y1q)为最小能耗绕转点;(x2q,y2q)为最短时间绕转点。
2.4 编队重构
无人机编队在一些未知环境中飞行,威胁和障碍的出现在时间上和空间上都是随机的;无人机编队在执行任务时可能经受意外事故或者人为攻击而受损。当发生这类情况时就需要进行编队重构,进而保证无人机编队的生存能力和任务完成能力。编队重构[16-20]是指无人机编队在行进过程中遇到突发情况,需要重新组织队形。相对于编队集结,编队重构有更多的约束条件。例如当出现成员退出时,就要重新设计合理队形;当遇到障碍物时,不仅需要设计合理队形,而且还要合理设置队形所处位置,从而使每一架无人机都能安全通过障碍物。队形中的变量包括Bmiddle=(xmiddle,ymiddle)、di以及夹角θi,具体增加的约束方程需要根据实际情况而定。
以6架无人机变换队形从两障碍物之间通过为例,如图2所示。
利用运动分解可以将无人机的重构问题分解为集结和通过两个部分。首先根据障碍物情况为无人机设计合适的通过形状 (di,θi)(i=1,2,…,6)。然后基于2.2节中的最小能耗和最短时间模型进行集结。编队重构问题中,无人机集结之后还有后续行为,因此对于无人机的方向协同有着更高的要求,所以这里采用Dubins航迹。
已知无人机i的初始位置为Ai= (xi,yi),初始航向为βi,集结目标位置为Bi= (xmiddle+dicosθi,ymiddle+disinθi),航向为β′i,其中只有(xmiddle,ymiddle)是未知量。对于确定的带航向的两点 (Ai,βi)和(Bi,β′i),如果无人机的最小转弯半径固定,则存在唯一的Dubins曲线,记其长度为Di。最小能耗和最短时间模型分别为
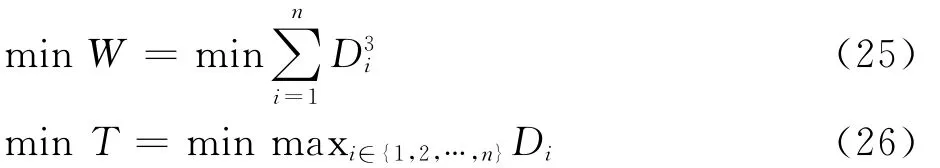

图2 编队重构Fig.2 Formation reconfiguration
由于Dubins曲线没有显性表达式,无法利用最小二乘进行求解,因此采用遍历搜索。遍历全局空间的计算量较大,但是通过设置合理的限制条件可以缩小解的搜索空间,从而减小计算量。如为了保证最大安全性,可以限制无人机编队从障碍物正中间通过,从而(xmiddle,ymiddle)的搜索空间为两障碍物连线的中垂线。最后再加上向障碍物移动的运动分量,就可以实现安全通过障碍物。
3 实验验证
3.1 编队集结
本模型是在已知所有无人机位置以及周围环境条件下的规划方法。首先初始化6架无人机为随机形状,然后根据指令要求形成边长为200的正六边形编队。图3描述了目标正六边形上下边平行于x轴时的最小能耗与最短时间变换时目标队形的位置情况,即θi为常数时的队形变换目标位置。图4描述了目标队形为平面任意正六边形时的最小能耗与最短时间变换时目标队形的位置情况,即θi为变量时的队形变换目标位置。在利用模型计算出各无人机的目标位置后,无人机以匀速直线运动前往目标点。
表1列出了图3中6架无人机实行θi为常数时的队形变换前各无人机的位置以及最小能耗变换和最短时间变换后的坐标位置。

图3 θi为常数时的变换Fig.3 Transformation with constantθi
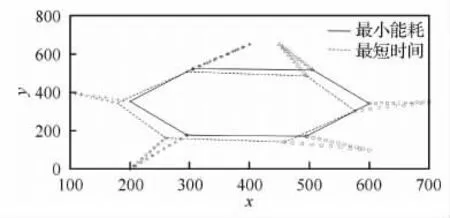
图4 θi为变量时的变换Fig.4 Transformation with variableθi
表2列出了图4中6架无人机实行θi为变量时的队形变换前各无人机的位置以及最小能耗变换和最短时间变换后的坐标位置。
表3的最优效率结果符合最优化目标,且θi为变量时,由于少了θi的约束,其最优效率(包括能耗以及时间)结果要优于θi为常数时。
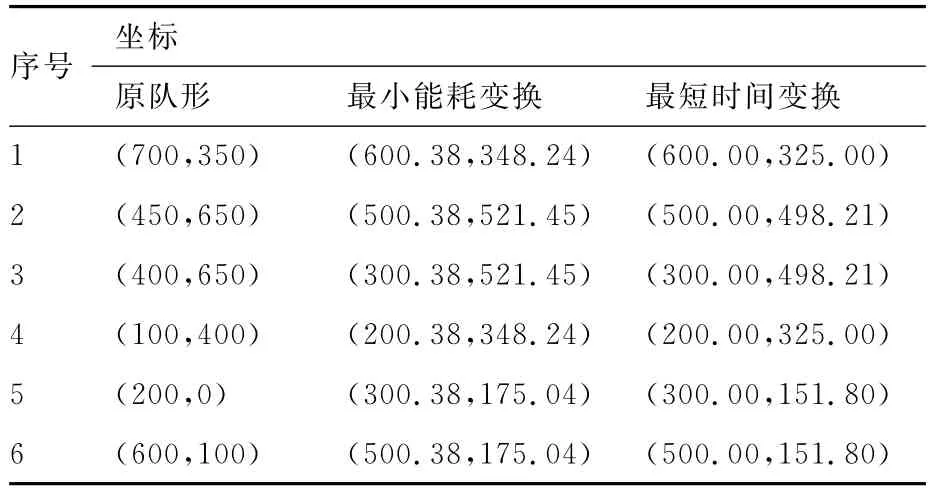
表1 固定θi变换时各无人机的坐标Table 1 Coordinates of each Unmanned Aerial Vehicle(UAV)when transforming with fixedθi

表2 不定θi变换时各无人机的坐标Table 2 Coordinates of each UAV when transforming with variableθi
表3 编队集结各无人机移动的距离Table 3 Distance passed in UAV’s aggregation
3.2 编队保持
为了便于观察,首先设计一个具有明确队形方向的编队队形,然后进行顺时针旋转θi=π/2。变换结果如图5所示。

图5 固定队形旋转Fig.5 Rotation with fixed formation
从表4可以得到无人机编队刚性顺时针旋转90°的最小能耗为19 362 456θ3c,最短时间为180.28θa。

表4 刚性旋转各无人机的绕转点和移动距离(θi=π/2)Table 4 Rotation center and distance passed in UAV’s rotation(θi=π/2)
3.3 编队重构
随机队形的无人机编队在行进过程中突遇两个障碍物,需要缩小队形从两个障碍物之间通过。首先需要设计一个较窄队形,以便于所有无人机均能顺利通过障碍物,其次为了保证最大安全性,需要将无人机编队的中心设置在两个障碍物的中垂线上,最后让无人机编队沿着中垂线通过障碍物。已知障碍物1设置于(800,500),障碍物2设置于(700,673.2)。
首先计算障碍物的中垂线以及障碍物之间的距离以便于设计合理目标队形。表5给出了一种可行的队形设计。

表5 无人机偏队的目标队形Table 5 UAV formation’s target formation
图6为无人机编队重构队形从障碍物中间通过示意图。将无人机UAVi的速度分解为vi=,其中为原队形向目标队形进行集结的速度,为无人机编队向目标方向前进的速度。合理设置速度分量的大小可以实现安全高效通过障碍物。当无人机编队距离障碍物过近时,可以增大,减小,甚至可以将置为0以先实现原地队形变换;当无人机编队距离障碍物较远时,只要满足在到达障碍物前形成目标队形,可以适当减小以节约能源,增大以减小编队到达目标点的时间。
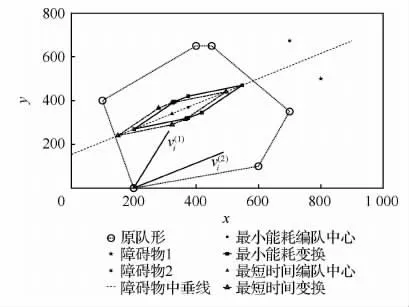
图6 无人机编队重构队形从障碍物中间通过Fig.6 Going through obstacles by formation reconfiguration
3.4 避撞策略
无人机均进行匀速直线运动可能会发生碰撞情况。如图7所示,6架不同起点的无人机对一静止目标进行快速包围,是一种典型的θi未知时的最短时间集结问题。
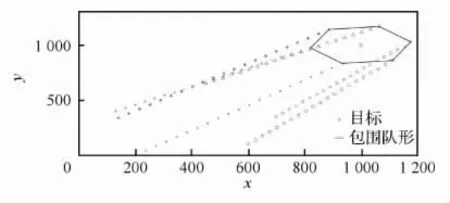
图7 静止目标包围Fig.7 Surrounding stationary target
为了防止编队成员之间发生碰撞,实行变高避撞。虽然不一定是最优,但是改变飞行高度可以有效解决碰撞冲突,另外无人机执行任务时一般飞行距离较远,在远距离情况下,实行变高飞行的路程代价相对较小。具体流程如下:
1)在轨迹图上寻找距离较近的点组。
2)计算各无人机到达该点组时的时间,如果时间差小于安全时间,则标记为冲突点。其中,安全时间等于无人机间的最小安全距离除以经过该冲突点组所有无人机的最小速度。
3)计算发生冲突时,各无人机离各自终点的距离,距离越大的优先级越高。
4)优先级低的无人机将会发生冲突的轨迹点上移。
4 结 论
1)本模型的最优效率指标是利用路程推导的,具有一般性,可适用于多类无人机。
2)将编队保持视为编队整体的平移和旋转,因此仅适用于松散的无人机编队,紧密无人机编队和有转弯半径的固定翼无人机无法绕内点进行旋转。
3)无人机编队要保持一定队形,各无人机的速度和航向都必须要保持一致,本文没有考虑各无人机时间协同到达目标点后的速度协同问题,将在下一步研究中进行考虑。
由于无人机防撞是一个非常复杂的问题,本文只简单考虑了轨迹规划时的编队成员之间的避撞。

