石英灯阵模拟非均匀气动加热的功率优化

朱言旦，魏东，刘深深，曾磊，＊，桂业伟

1.中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000 2.中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

结构热试验是对飞行器相关材料和结构进行长时间热响应考核的重要试验方法［1］，而石英灯阵辐射加热以其热惯性小、便于控制、方便调整结构、对复杂结构适应性强等特点在高超声速飞行器结构热试验中获得广泛应用［2］。

对于利用石英灯阵模拟均匀气动加热，目前国内外已进行了大量的研究，发展了包括理论解析方法［3－5］、蒙特卡罗方法［6］及其相关简化方法［7］在内的数值模拟方法，并开展了相关试验研究。对于利用石英灯阵模拟大面积的非均匀气动加热，目前一般做法是将试验区域进行离散分区［8－9］，分区内仍旧利用石英灯阵模拟均匀热流，分区之间利用隔板等隔断措施来避免分区之间的干扰以达到各分区之间非均匀热流分布的效果。虽然分区模拟的方法可以很大程度上简化控制，并已 广 泛 应 用 于 材 料［10］、结 构［11－12］甚 至 是 整机［13］的结构热考核试验中，但有限的分区导致石英灯阵得到的非均匀热流分布呈区块性非均匀分布，分区边缘处热流存在间断，能够达到的模拟加热过程与实际飞行条件下加热过程有较大差异，给试验过程带来较大误差。

同时航空航天技术的发展对飞行器综合一体化热／能量管理系统提出越来越高的需求，这就要求在结构考核试验中同时实现表面热流加载和进入飞行器内部热量的精确控制，而传统的分区模拟通常是极限考核，越来越难以满足精细化模拟的需求。为了利用石英灯阵得到整体连续性、光顺性、局部分布特征更好的非均匀热流分布，朱言旦等提出了一种通过异化调控各石英灯功率来实现非均匀气动加热的非分区模拟方法［14］，该方法基于遗传算法通过反向设计优化石英灯阵中各灯的功率实现非均匀气动加热的石英灯阵非分区整场模拟，并对大面积二维非均匀气动加热进行了模拟，初步验证了该非分区模拟非均匀气动加热方法的可行性，但对于梯度较大的位置热流模拟结果偏差较大。

利用石英灯阵进行非均匀气动加热非分区模拟试验时，通常需要根据试验表面的温度实时计算灯阵各灯功率，而基于遗传算法的功率优化算法很难满足实时性的需求，为进一步探索并改进非分区模拟非均匀气动加热的方法以满足快速设计需求，并且对大梯度热流模拟提出可能的改进方向，本文建立了对石英灯阵功率进行异化调控的线性分析方法，对石英灯阵直接模拟非均匀气动加热的优化问题进行了研究。

1 理论方法

1.1 石英灯阵热流分布理论解析方法及验证

求解石英灯阵热流分布的方法有理论解析方法（THE）、蒙特卡罗方法（MCM）及其相关简化方法等，文献［15］对不同方法进行了对比分析，结果表明，理论解析方法和蒙特卡罗方法均可较好地进行简单灯阵（平直石英灯＋平面反射屏）的优化设计，但理论解析方法具有实现简单、计算效率高的优点。因此，为简化计算，本文采用理论解析方法进行计算分析。理论解析方法［3］将单个石英灯简化为一个表面均匀的黑体，通过理论推导获得单个石英灯热流分布。以单个石英灯中心在平板测试面上的投影位置为原点，石英灯轴向为x轴，垂向为y轴建立坐标系，如图1所示，则单个石英灯在平板接收面上的辐照热流可以表示为

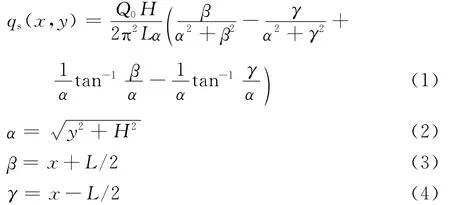
式中：qs（x，y）为平板上坐标为（x，y）处的辐照热流；Q0为单个石英灯发射功率；H 为单个石英灯中心距平板的距离；L为单个石英灯有效加热长度，此处取为灯丝发热长度。

石英灯阵热流分布由单灯热流分布叠加获得。文献［14］指出，在石英灯阵高度和间距较小时，线性叠加和直接模拟结果会有明显差异。本文的研究对象为如图1所示的由10支石英灯均匀并排排列组成的石英灯阵，石英灯有效加热长度为200mm，外径为10mm，间隔为20mm，石英灯阵高度为20mm。对于一维排列的石英灯阵，沿石英灯轴向的热流分布不可控，故以石英灯垂直方向的热流分布表征石英灯阵的热流分布。每支石英灯加载功率为1 000W，蒙特卡罗方法中光束模拟量为1 000W－1。叠加计算结果与蒙特卡罗方法直接模拟结果对比如图2所示。理论解析方法叠加得到的石英灯阵热流分布结果与蒙特卡罗直接模拟结果符合良好，中间较为均匀的区域偏差在2.5%以内，而通常蒙特卡罗方法计算结果与试验结果偏差在5%以内，因此可以利用理论解析方法进行石英灯阵功率优化配置分析。

Fig.1 Quartz lamp array

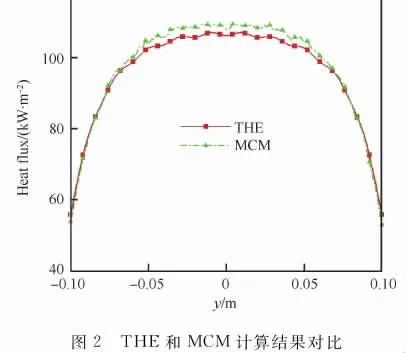
Fig.2 Comparison of THE and MCM computational results

1.2 石英灯阵功率优化的快速线性分析方法

石英灯阵功率优化问题本质上是一个已知试验面上的热流分布求解石英灯阵各灯功率的辐射反问题。由式（1）分析可知，基于理论解析方法的石英灯阵热流与功率之间存在线性关系，文献［16］的计算和试验结果也获得了同样的规律。因此，对于由n支石英灯组成的石英灯阵，如果共有m个热流测点，则可以列出如下方程组：

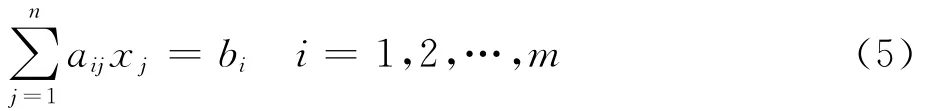
式中：xj为第j支石英灯的功率；aijxj为第j支石英灯在第i个测点上的热流；bi为第i个测点上的热流。

将式（1）写成矩阵形式可得

式中：

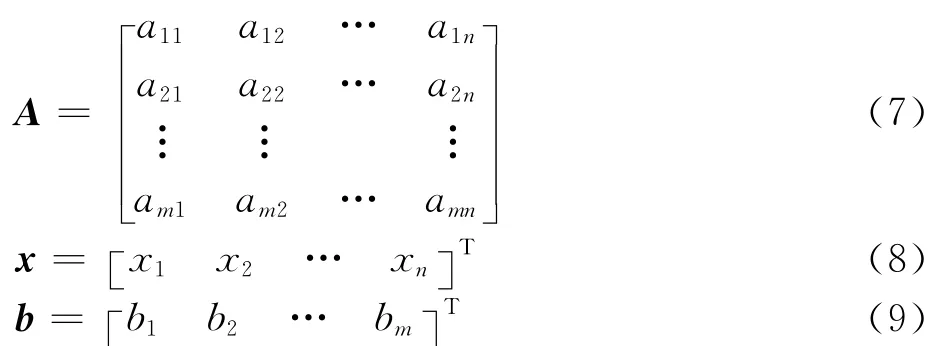
为便于分析和求解，在式（6）两边分别左乘AT得

式（11）中，如果m≥n且系数矩阵B是满秩的，则线性方程组有唯一解，可通过求解式（11）获得石英灯阵各灯功率。

2 结果分析与讨论

对于图1所示的石英灯阵，给定每支灯的功率为1 000W，在y轴上±100mm范围内均匀设置11个测点，基于理论解析方法得到了该功率下的热流分布及11个测点的热流，对于采用理论解析方法计算得到的测点热流值分别叠加±0%、±2.5%、±5.0%、±7.5%、±10.0%以内的随机偏差，由叠加偏差后的热流分布通过快速线性分析方法计算得到了各灯的功率配置（P1～P10），如表1所示。可以看出，随着热流叠加偏差的增加，功率计算结果与预定功率偏差明显增加。以不同状态下的功率计算结果为加载功率，计算获得石英灯阵的热流分布如图3所示。可以看出，随着叠加偏差的增加，热流分布结果与初始状态的偏差逐渐增加，但偏差量在叠加的随机偏差范围之内。

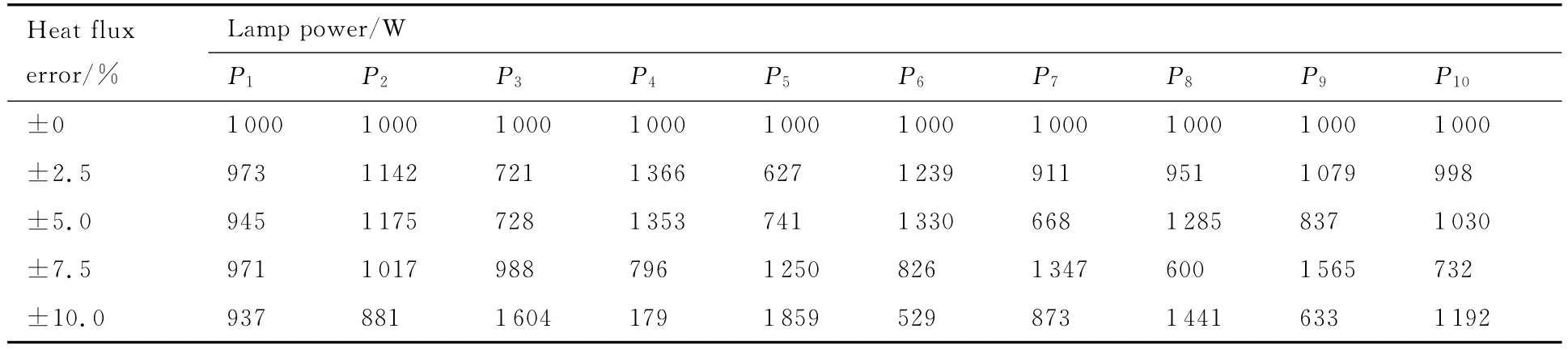
表1 不同热流偏差下的功率计算结果Table 1 Power computational results with different heat flux errors

在数值分析中，将矩阵的范数和其逆矩阵的范数之积称为这个矩阵的条件数，条件数表示了矩阵计算对于误差的敏感性，条件数越大矩阵计算对误差越敏感，小的输入误差会带来越大的结果偏差。计算得到不同测点范围和测点数目时系数矩阵的条件数（2范数），如图4所示。不同测点范围和测点数目时，系数矩阵的条件数一直保持在较大的水平，说明石英灯阵功率优化问题的功率优化结果对热流的输入比较敏感，如果缺少有效的抑制手段，可能会对石英灯功率的裕度提出较高要求。对于相同的测点范围，不同测点数目时条件数变化较大，但随着测点数目的增加呈现收敛的趋势。对于相同的测点数目，不同测点范围时条件数变化较大。整体上看，当测点范围基本等于灯阵尺度时，条件数相对较小且随测点数目的增加变化幅度不大。综上所述，测点范围和测点数目对条件数影响较大，因此可以通过优化分析选择合适的测点范围和测点数量得到相对稳定的系数矩阵。

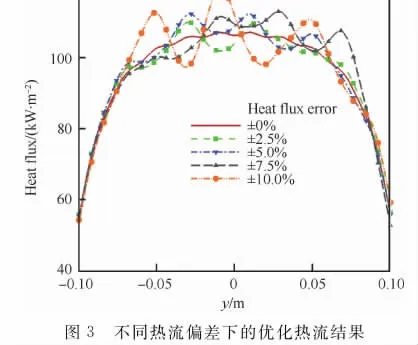
Fig.3 Optimized heat flux results with different heat flux errors

为验证线性分析方法（LM）进行石英灯阵功率配置优化得到给定热流分布的有效性，选定了3个典型热流状态进行分析，并同时采用遗传算法（GA）进行结果对比。其中，Case 1以实现100kW／m2的均匀热流为目标，Case 2以实现20～90kW／m2的线性变化热流为目标，Case 3以实现30kW／m2阶跃到80kW／m2的阶跃热流为目标。灯阵热流分布优化设计的遗传算法流程［14］如图5所示。文中遗传算法采用64位二进制编码，交叉及变异概率分别取为0.8和0.005，目标函数如式（14）所示，各参考点权重相同。选取种群规模为500，优势群体10%，进化到5 000代时停止。

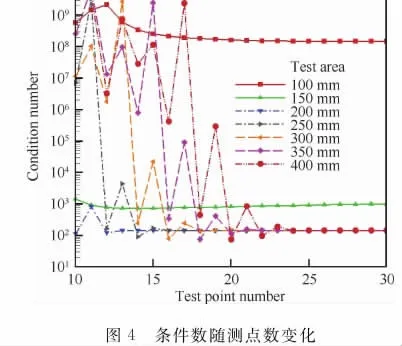
Fig.4 Variation of condition number with test point number

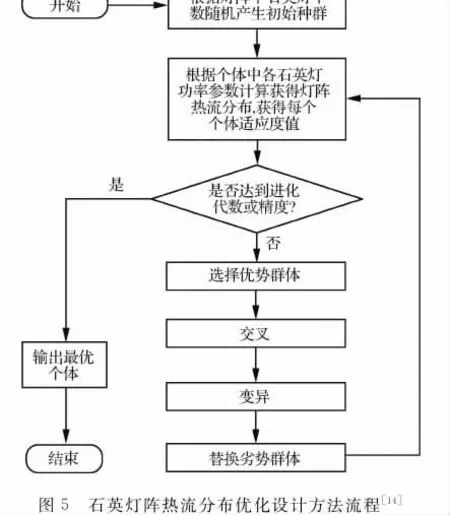
Fig.5 Process of optimization design method for quartz lamp array heat flux distribution［14］

式中：x为长度为n的优化参数向量，此处为灯阵中各灯功率，约束条件为xi∈ ［0，Pmax］，Pmax为石英灯允许加载的最大功率；m为测点数目；wi为测点i的权重；q′i为测点i的目标热流；qi为测点i的计算热流，qi是x的函数。

在配有Intel i7处理器的计算机进行单机计算，采用线性分析方法求解一个状态耗时约7.4×10－6s，采用遗传算法求解一个状态耗时约296.3s。不同状态下各石英灯功率计算结果如表2所示。可以看出，采用线性分析方法与遗传算法求解的结果基本趋势具有一致性。Case 3中线性分析方法的结果个别石英灯的功率为0W，对应位置遗传算法得到的功率值也比较小，这说明该位置的石英灯可能是不必要的，或者说该位置的石英灯间距可以适当增大。考虑石英灯功率、数量和位置的综合优化问题已超出线性分析方法的范围，本文暂不予进行更多讨论，但这也给后续更为复杂热流的模拟优化提供了一条具有参考性的方向。

将表2中的优化功率分别作为石英灯阵的功率进行计算获得不同状态下的石英灯阵热流分布，如图6所示，图中refer表示优化目标热流。对于Case 1，线性分析方法与遗传算法求解的热流优化结果基本一致，中间区域基本模拟了100kW／m2的均匀热流，两端有较大的波动偏差。从图2可以看出，石英灯阵两端热流衰减迅速，为了使两端热流尽量满足100kW／m2的均匀热流，两端的石英灯优化功率会偏大，又由于石英灯阵的不连续性，热流分布本身会有波动形起伏，这就导致优化结果两端存在较大的波动偏差。而且，应该注意到的是，遗传算法优化得到的热流分布具有明显的不对称性，说明其并没有收敛到全局最优解，这也可以在一定程度上反映出该优化问题对输入的敏感性。对于Case 2，线性分析方法与遗传算法求解的热流优化结果基本一致，中间区域基本模拟了20～90kW／m2的线性变化热流，两端有较大的波动偏差，与Case 1的规律基本一致。对于Case 3，线性分析方法与遗传算法的热流优化结果和规律较为一致，基本得到了高低热流平台，但都有较大的波动，中间过渡区域比预定过渡趋势缓和很多，说明利用石英灯阵模拟大梯度的热流分布具有一定的难度。

综上所述，对于选定的3个典型化状态，线性分析方法与遗传算法求解的热流优化结果基本一致，一定程度上线性分析方法求解的热流结果与比遗传算法求解的热流结果还要更符合目标热流，两种方法计算结果的中间区域均与目标结果符合较好，两端则有较大偏差，石英灯阵在模拟大梯度热流分布方面具有一定的困难。

表2 各灯功率计算结果对比（测点范围：±100mm）Table 2 Comparison of calculation results for each lamp power（Test area：±100mm）

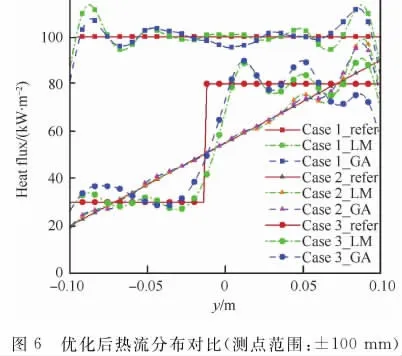
Fig.6 Comparison of optimized heat flux distributions（test area：±100mm）

由上面的分析可以知道，石英灯阵热流分布的可控区域为中间部分区域，因此，下面将缩小测点分布范围到－75～75mm，保持其他条件不变，进行计算分析。不同状态下各石英灯功率计算结果如表3所示。缩小测点分布范围后，线性分析方法与遗传算法的结果基本趋势是一样的，但个别石英灯的功率依然有较大的差别。

从热流结果来看（图7），由于减小了测点分布范围，即测点基本分布在热流可控的区域，优化热流结果较之前有了较大的改善，遗传算法优化结果较线性分析方法优化结果波动较大，说明对于此类问题，常规的遗传算法很难收敛到全局最优解，可以考虑采用多种群遗传算法等全局寻优能力更强的策略。对于Case 3，优化结果在高低热流平台的优化结果有较大改进，但在大梯度区域依然存在较大的波动偏差，说明石英灯阵模拟大梯度热流分布有其本身的缺陷，这跟热辐射传输的物理规律是符合的。

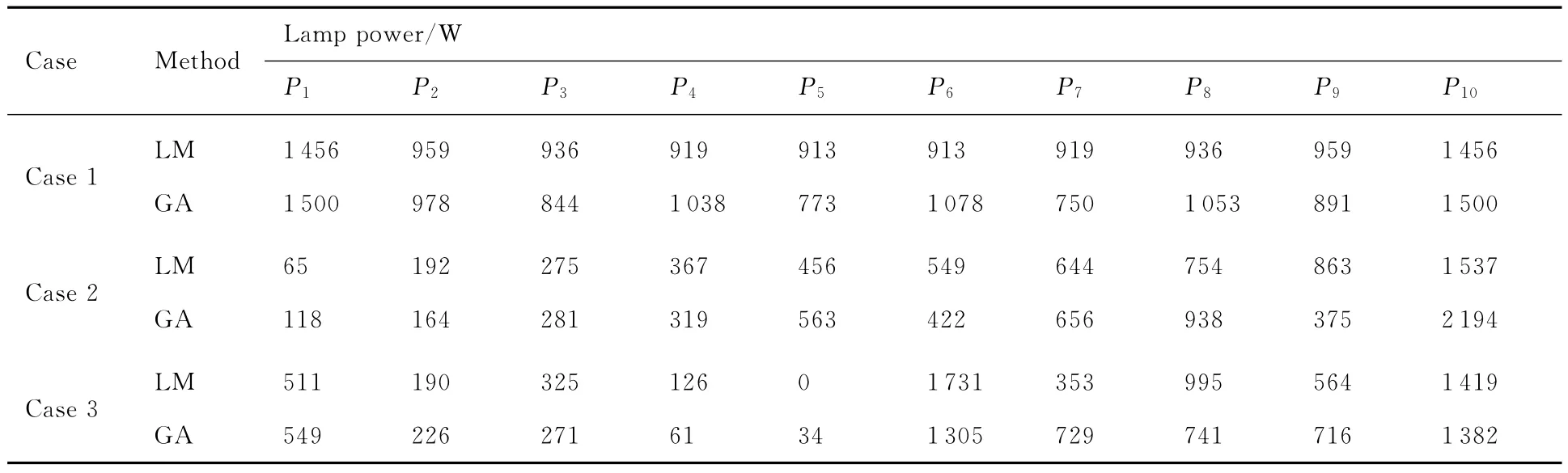
表3 各灯功率计算结果对比（测点范围：±75mm）Table 3 Comparison of calculation results for each lamp power（Test area：±75mm）

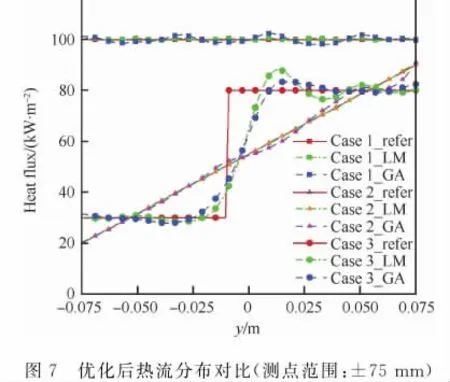
图7 优化后热流分布对比（测点范围：±75mm）Fig.7 Comparison of optimized heat flux distributions（test area：±75mm）

3 结 论

1）建立的石英灯阵功率优化的快速线性分析方法基本可以对石英灯阵功率配置进行快速优化。对于比较平缓的热流分布可以获得较好的热流模拟结果，对于大梯度热流分布也能获得与遗传算法较为一致的热流模拟结果和规律，具有较好的工程适用性。

2）模拟非均匀气动加热的石英灯阵功率优化问题的功率优化结果对热流的输入比较敏感。热流测点的分布范围和测点数量对问题系数矩阵的条件数影响较大，但可以通过优化选择合适的测点范围和测点数量得到相对稳定的系数矩阵。

3）对于大梯度热流分布以及更为复杂的热流分布，可能需要结合石英灯阵的石英灯数量和位置进行综合优化，后续将开展相关研究以更好地适应工程需要。