异形涤纶的吸湿快干性评价

王金花

中国纺织科学研究院有限公司 北京 100025

1 前言

涤纶的许多物理、化学性能都优于天然纤维，但由于涤纶是疏水性纤维，大分子中缺乏亲水基团，吸湿性差，导致其易产生静电、易沾污和染色困难等问题，影响了服装的穿着舒适性。改进涤纶织物的吸湿性能，改善其织物穿着的舒适感受，是涤纶研究中的一个重要方向。

对涤纶的改性，主要是通过化学改性和物理改性的方法赋予其较高的吸水性和疏水性，以提高涤纶织物穿着的舒适感[1]。为保留涤纶织物的特性，提高其服用舒适性，世界各大化纤公司都相继开发出了吸湿快干的异形涤纶[2]，使纤维具有沟槽结构，并且在纤维壁上设计出许多微孔，这样水气就可以顺着沟槽和微孔导出。

虽有较多文献报道对织物的吸湿快干性进行了研究[3-5]，但针对纤维的吸湿快干性评价报道较少，本文选取了较为常规的“+”字形截面异形涤纶纤维，进行了吸湿快干性评价。通过对纤维保水率、失水率和干燥速率的测定，结合纤维表面沟槽对其吸水和排水能力的影响，总结出影响纤维吸湿快干性的因素。

2 实验部分

2.1 材料和试剂

PET切片，中国石化集团洛阳石化分公司提供，特性粘数：0.678 dl/g。工作中使用的试剂均为分析纯。

2.2 纺丝和牵伸

在中国纺织科学研究院有限公司的单螺杆纺丝机上进行纺丝，喷丝板为“+”字形36孔，纺丝速度3000m/min。英国万能电子强力机INSTRON-2340测试纤维的断裂强度和断裂伸长率等力学性能，夹持距离200mm，拉伸速度200mm/min。

2.3 扫描电镜观察

用日本JEOL JSM-6360扫描电子显微镜（SEM）观察纤维侧面和横截面形貌。

2.4 吸湿快干性测试

2.4.1 保水率测试

将纤维脱油后干燥并称重，记录质量W，再完全浸入蒸馏水中1h，取出后自然排水2 min，然后装入底部带有小孔的离心套管中以2000 r/min的速度离心脱水5min，取出纤维迅速放入天平中称重，记录质量W1，根据公式（1）计算纤维保水率。

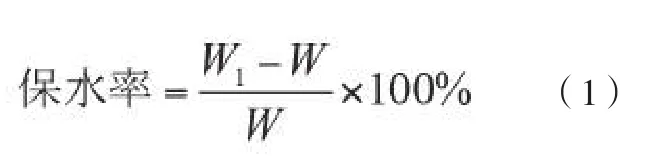
2.4.2 干燥速率

测试保水率的纤维不取出天平，直接在托盘上每隔5min记录其质量的变化，直到纤维重量达到平衡，并根据公式（2）算出纤维失水率，然后对失水时间作纤维干燥速率曲线，称量过程中保持天平内湿度为75%。

图1 纤维横截面和侧面的SEM照片

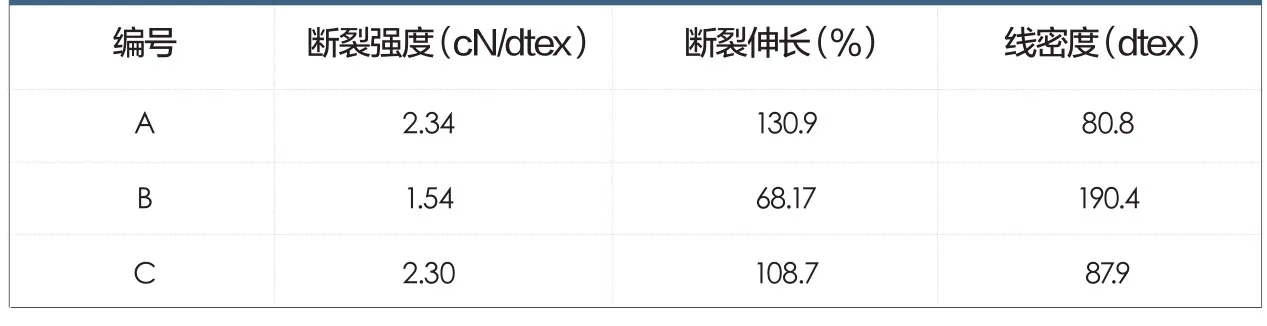
表1 纤维的力学性能

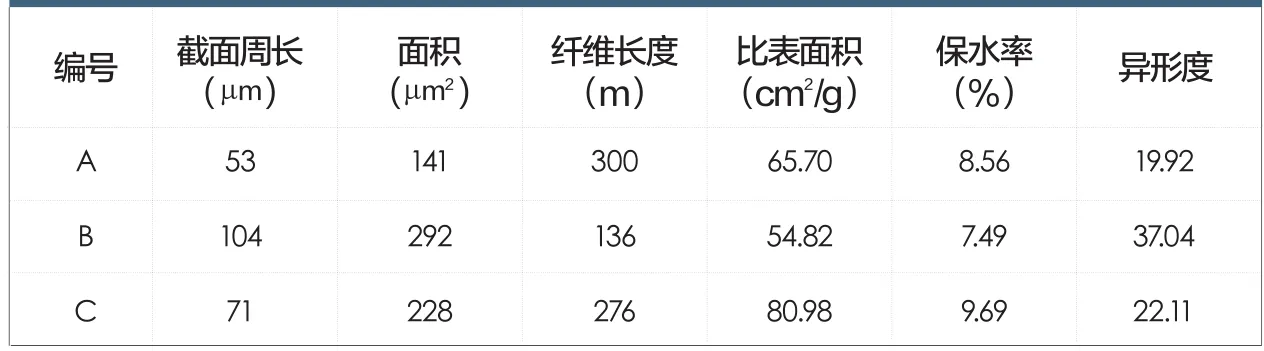
表2 三种纤维尺寸参数和保水率值

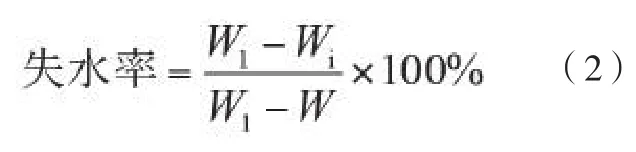
3 结果和讨论

3.1 纤维力学性能

纤维的力学性能列于表1，A、B、C三种纤维为不同纺丝温度下的纤维样品。纤维B的线密度最大，纤维最粗，而A和C线密度接近，纤维较细，纤维B力学性能也弱于其他两种纤维。

3.2 纤维截面和侧面观察

经SEM 观察纤维截面和侧面，如图1所示。纤维A截面形状与B和C有明显区别，“十”字形凹槽轮廓不明显；B 和C 则呈规则“十”字形，纤维表面的凹槽形状在图中也很清晰，B纤维较粗，表面凹槽宽大；C纤维表面凹槽明显。

3.3 纤维的异形度和比表面积

纤维截面的异形度是指非圆形纤维截面形状凹凸的尺度，异形度越大表明形状越曲折。异形度可以用分支度来表示[6]，圆的分支度为12.6 ，分支度越高说明异形度越大，分支度 B 可用式(3)来计算。

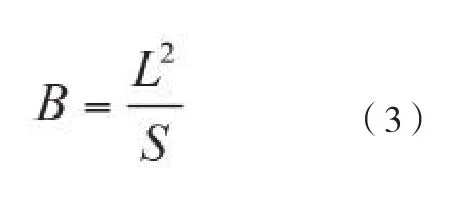
式中： L 为纤维截面周长（µm）; S为纤维截面面积（µm2）。

将3种纤维的截面图形投影到坐标纸上[7]，各选出有代表性的3个，分别计算其周长和面积并带入式（3）进行计算，最后取其平均值作为该种纤维的分支度。并根据公式（4）计算纤维比表面积（Sg），所得结果如表2。

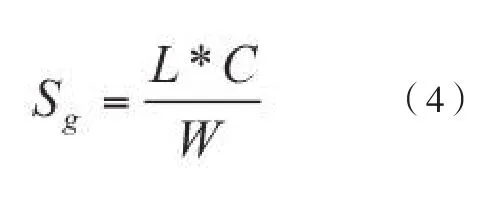
式中： L 为纤维截面周长（µm）; C为纤维长度（m）；W 为纤维质量（g）。

3.4 纤维吸湿快干性

3.4.1 保水率

三种涤纶保水率列于表2。保水率是单位绝干重量纤维所含有的不能用机械方法除去的水分，以重量百分率表示，一般对保水率的测试方法都采用离心法[8]。

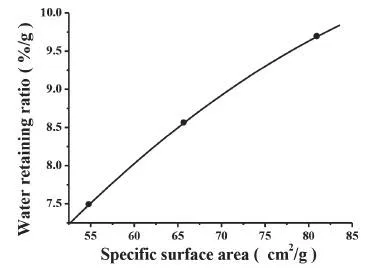
图2 三种纤维保水率与比表面积的线性关系曲线

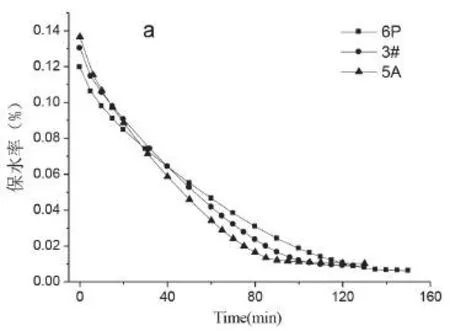
图4 消除比表面积后纤维干燥速率曲线

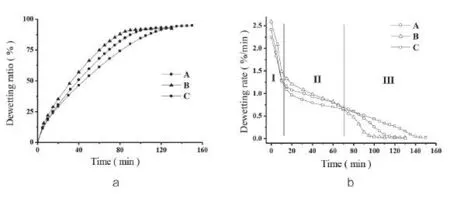
图3 纤维干燥速率曲线

C和A线密度接近，但前者截面呈规则“十”字形，纤维表面有凹槽，所以截面面积大，异形度大，比表面积最大，所得保水率也最大；B虽表面凹槽轮廓清晰，但因纤维较粗，比表面积最小，所得保水率值最小；而A虽表面凹槽不明显，但比表面积介于两者之间，所以保水率也介于两者之间。将三种纤维的保水率(Y)对比表面积(X)作图，两者呈线性关系，Origin拟合得相关系数为1的曲线，方程如下：

Y = -1.25966 + 0.21072 X - 9.32443 10-4X2

可见对疏水性纤维而言，纤维纺异形后增大了比表面积，增加了表面的凹槽，使纤维毛细效应增强，从而使纤维的保水率提高。

3.4.2 干燥速率

根据公式（2）计算对应时间的纤维失水率值，对时间作图，得到纤维失水速率曲线如图3。

由图3a，在干燥放湿过程达到平衡前，C失水率值始终小于其它两种纤维，可见纤维C能够吸收和保留水的能力最强。将图3a中曲线微分，所得纤维的失水速率曲线如图3b，失水速率曲线可被分为三部分，分别对应图中Ⅰ、Ⅱ、Ⅲ，第Ⅰ部分为0～10min，速率变化快，说明此段时间是纤维表面水的干燥过程，三者失水速度都很快且接近一致，第Ⅱ部分为10～70min，速率变化明显趋于缓慢，此段时间为纤维沟槽中存储的水的干燥过程，因为纤维为十字形截面，沟槽宽阔，所以沟槽储存的水相对较少，三者速率接近，70min后为第Ⅲ部分，此段时间为纤维间相交或相并部分存储在沟槽中的水的干燥过程，与纤维的堆砌程度有关，在此段时间C失水最快，而B则最慢。原因为C纤维较细，比表面积最大，所以失水最快，但因其保留的水份最多，所以达到放湿平衡的时间最长，而B纤维较粗，比表面积最小，所以失水最慢，保留的水最少，最先达到失水平衡，而A则介于两者之间。

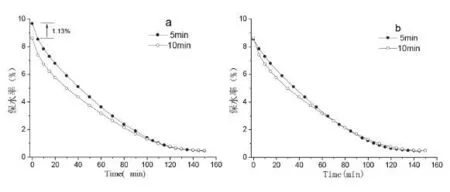
图5 纤维C离心脱水5min和10min的干燥速率曲线

3.4.3 放湿回归方程的建立

根据文献[9]，纤维吸湿放湿的理论曲线(在平衡过程中回潮率与时间的关系曲线) 为指数曲线，此处干燥速率曲线同样适用，失水率对时间的回归方程通式为：

y = a ( 1 - e-bt)

式中a 、b为常数。

利用Origin 数学分析软件对实验结果进行曲线拟合，得其拟合方程：

w = a ( 1 - e-bx)

纤维A为：W =95.61332

( 1- e-0.0240t) R2=0.98104

纤维B为：W =94.71456

( 1- e-0.02851t) R2=0.98489

纤维C为：W =97.05841

( 1- e-0.02014t) R2=0.98452

所得回归方程与纤维吸、放湿的经验方程式[10]W= Wp+(W0+Wp)e-at基本一致，在式中： W 为纤维干燥过程中任意时刻t 的保水率(%)；Wp为纤维干燥平衡的保水率(%)；W0为纤维的初始(t=0)保水率(%)；a为干燥系数。

将图3a中纤维的保水率除以比表面积，消除比表面积对纤维失水速度的影响，所得曲线如图4。

纤维失水速率受纤维的比表面积大小、纤维表面的沟槽形状和深度[11]、纤维的堆砌程度等共同影响，但纤维的比表面积对其影响最大。由图4，消除比表面积的影响以后，纤维干燥速率曲线和图3有明显区别。纤维比表面积相同时，堆砌程度决定了失水速率，B纤维较粗，所以堆砌程度较小，失水速率越大，最快达到失水平衡。

3.5 离心脱水时间的影响

将纤维离心脱水的时间增加为10min，所得干燥速率曲线如图5a。离心时间增长，使纤维的初始保水率值减小，两者相差1.13%。将5min曲线的高出1.13%的部分取掉，剩余的部分计为从零开始，如图5b，可见两条干燥速率曲线基本相同50min 后接近于重合。所以离心时间的不同，只改变了纤维的初始保水率值，而对纤维的干燥过程几乎没有影响。

4 小结

1）纤维纺异形后极大地增加了比表面积，而且纤维表面的沟槽提高了芯吸效应，使纤维的吸水保水能力提高。

2）比表面积相同时，纤维的相互堆砌程度越小，干燥速率越大。

3）离心时间的不同，只改变了纤维的初始保水率值，而对纤维的干燥过程几乎没有影响。