面向地形类型区分的地表粗糙度算法比较研究

李玉茹，杨勤科，王春梅，吴 江

(西北大学 城市与环境学院，陕西 西安710127)

数字地形分析研究中，地表粗糙度指真实地表面与理想地表面(如大地水准面)在垂直方向上的偏离程度[1]，偏差越大，表面越粗糙，反之越平滑。地表粗糙度主要反映地表信息的高频率(短波长)成分，可以用来表示地球和星球表面的复杂程度[2-3]。地表粗糙度与诸多地表过程(如坡面径流、土壤侵蚀、地表灾害等)有关[1,4-6]，主要应用于地质灾害评价[7]、基本地形类型划分[8]、水土流失评价[9]及人口分布研究[10]等领域，因而量化地球表面的粗糙程度，是数字地形分析、地表过程分析和侵蚀地貌学的重要研究内容。

国内外学者提出了一组量化地表粗糙度的算法，Hobson[11]曾将粗糙度算法概括为3种，分别为比表面积、高程统计分布不规则性和垂直地面法向量的聚集程度。诸多学者对不同粗糙度算法进行了对比研究，Shepard等[12]利用收集的60个数据集对比分析了7种粗糙度算法，并对尺度依赖问题进行了探讨；Grohmann等[6]利用不同空间尺度和不同分辨率的数据对6种粗糙度算法进行了评价；Berti等[13]以滑坡识别为目的，利用数学合成表面和自然表面，对10种粗糙度算法进行了对比分析。Lane[4]和Smith[1]先后对地表粗糙度研究进行了比较全面的总结，认为有必要对不同研究者从不同角度提出的多种算法进行比较分析。目前，对各种粗糙度算法进行对比分析，并将计算的粗糙度结果用于侵蚀地形，特别是地形类型区分的研究鲜见报道。

本研究以SRTM3高程数据为基础，以区分地形类型为目标，选取文献报道的11种算法提取研究区的地表粗糙度，对比分析不同算法的优缺点，并探讨不同算法区分研究区地形类型的能力，旨在为地形类型分类和分区研究提供参考。

1 研究方法

1.1 研究区概况与数据来源

研究区覆盖了陕西、四川、甘肃、湖北、山西和宁夏6个省(区)的部分区域(29°54′06″N-36°08′48″N，104°54′37″E-110°58′36″E)(图1)，地理上包括黄土高原南部、秦岭、巴山和四川盆地东北部，总面积约38万km2。区内地形类型有平原、丘陵、山地(低山到中高山)，是对比分析各种粗糙度算法，研究各种算法对不同地形类型识别能力的理想研究区。

本研究使用的数据是从CGIAR-CSI网站(http://srtm.csi.cgiar.org/)下载的SRTM3高程数据。对下载的数据进行拼接并将投影转换为6度分带的高斯投影，中央经线为108°E，分辨率设置为90 m。

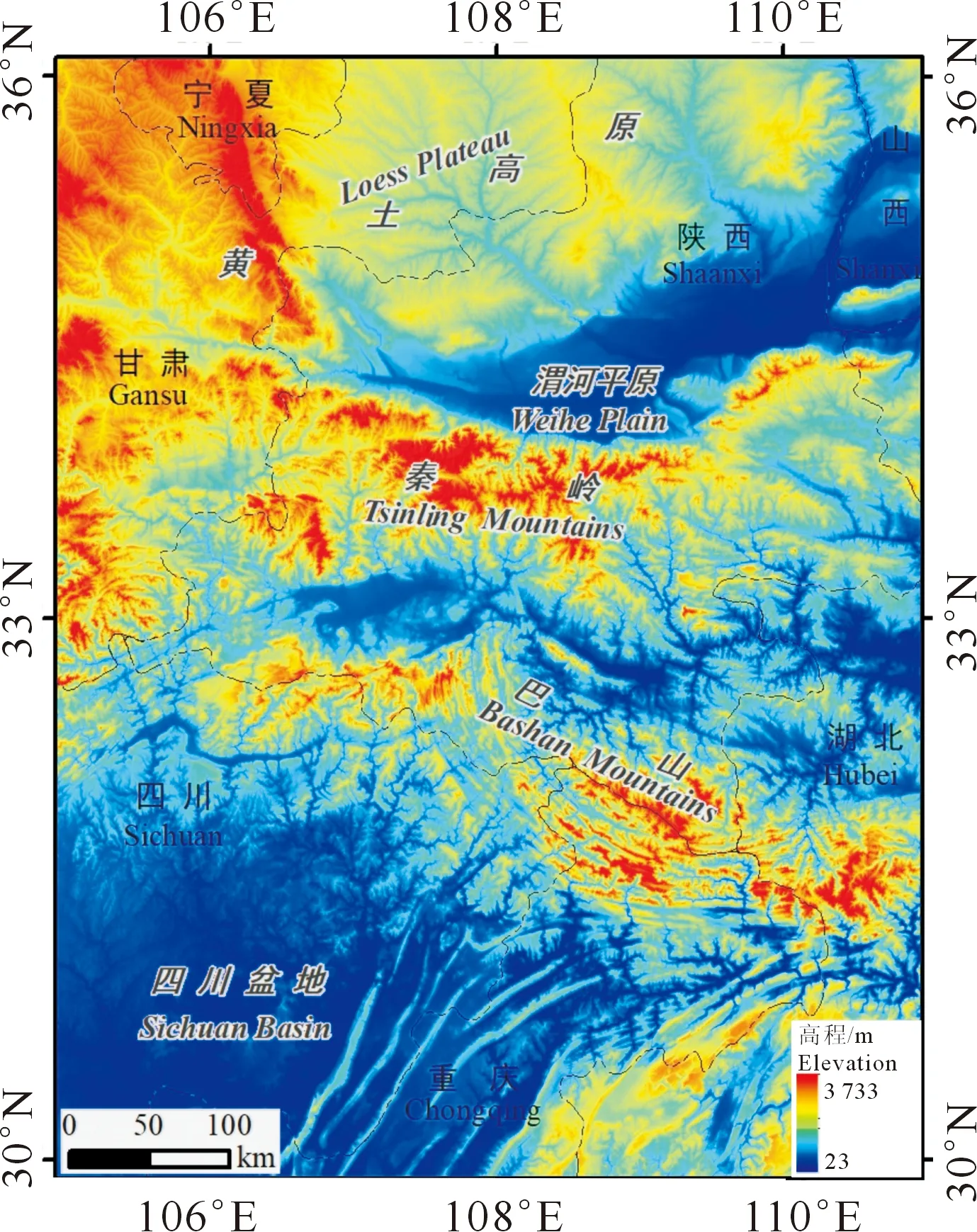
图1 研究区位置示意图Fig.1 Location of study area

1.2 地表粗糙度算法

本研究从相关文献中选取了以下11种粗糙度计算方法进行分析。参考Berti等[13]的研究，考虑到其计算结果均为粗糙度的量化表达，所以下文统一将这些计算方法称为算法。

(1)坡度算法[2]，简称“Slope”，计算公式为：

式中：S为坡度，p为中心像元在x方向上的变化率(高程梯度)，q为中心像元在y方向上的变化率(高程梯度)。

(2)局地高差算法[14]，简称为“Range”，计算公式如下：

R=Zmax-Zmin。

式中：R为局地高差，Zmax为移动窗口内像元最大高程值，Zmin为移动窗口内像元最小高程值。

(3)高程均方差算法[13]，简称为“RMSH”，计算公式如下：

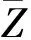
(4)高程均方根偏差算法[13]，简称为“RMSD”，计算公式如下：

式中：RMS_D为高程均方根偏差，Zc为移动窗口中心像元高程值，Zb为移动窗口边缘像元高程值。

(5)均方根坡度算法[13]，简称为“RMSS”，计算公式如下：

式中：RMS_S为均方根坡度,Δxb为中心像元至边缘像元的距离。

(6)绝对坡度算法[13]，简称为“AS”，计算公式为：

式中：A_S为绝对坡度，W为栅格大小。

(7)坡度标准差算法[13]，简称为“SDS”，计算公式如下：

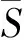
(8)面积比算法[6]，简称为“AR”，计算公式为：

式中：A为面积比。

(9)二维变异性算法[15]，简称为“γ”，计算公式为：

式中：V为二维变异性，(xi,yi)为第i个像元的空间坐标，h为滞后距。

(10)矢量离差算法[11]，简称为“VD”，计算公式如下：

式中：D为矢量离差，Ai为移动窗口内第i个像元的坡向。

(11)余弦特征值算法[16]，简称为“DCE”，计算公式如下：

C=ln(E1/E2)。

式中：C为余弦特征值，E1和E2为3×3方向余弦矩阵的归一化特征值。

除DCE外的其他算法都是数值越高代表地表越粗糙，对于DCE算法，利用计算出来的最大值减去计算结果，使其与其他算法保持一致。

1.3 数据分析方法

1.3.1 提取结果比较方法 在Python脚本语言的支持下，用3×3的矩形窗口使用邻域分析方法提取地表粗糙度。对于计算的各种粗糙度结果，利用以下方法进行分析。

(1)图像表面格局对比。研究所采用的11种算法计算的粗糙度结果数量级不同，因此利用极差标准化方法将提取结果统一拉伸到0～100。拉伸后的结果图像采用相同色带显示使其具有可比性。观察不同算法在不同地形类型区的图像表面，直观对比算法间的不同。

(2)相关性分析。采用ArcGIS中的Correlation函数实现，若2种算法提取结果的空间相关性越接近1，表明2种算法的相关性越强，可以相互替代。

(3)统计分布分析。提取每种粗糙度计算结果(极差标准化后)的统计特征值(平均值、标准差)和频率分布曲线，从统计分布角度对比算法的异同。

1.3.2 粗糙度计算结果低通滤波 粗糙度的计算结果主要反映地表的局地信息(高频成分)，但也包含了一部分相对低频的全局信息。考虑到地形类型是一个比较宏观的概念，因此为了区分地形类型，需要对粗糙度计算结果进行低通滤波，以剔除高频信息，保留相对宏观的地形信息；并对初步筛选出的粗糙度提取结果进行均值滤波处理。

1.3.3 地形类型区分能力分析 对滤波后的粗糙度结果从以下2个方面进行分析：

(1)典型断面分析。在研究区布设一条自北向南纵跨黄土丘陵、渭河平原、秦岭山地的断面，提取不同粗糙度滤波结果沿断面线的形态分布曲线，讨论不同算法区分地形类型的能力。

(2)频率曲线分析。单一地形类型条件下，坡度的统计分布呈单峰(正态)分布，而复合地形区(包含几种地形类型)的统计分布，是几个单一类型之和。据此，对比滤波后的粗糙度结果的频率曲线，根据频率曲线的波峰波谷分布分析不同算法区分地形的能力。

1.4 地表粗糙度计算与分析的技术路线

技术路线如图2所示。

图2 地表粗糙度计算与分析的技术路线图Fig.2 Procedure for surface roughness calculation and analysis

首先下载SRTM3高程数据，对高程数据进行拼接、投影转换等预处理，通过编程实现对研究区上述11种粗糙度的计算，然后从空间格局分析、统计分布分析、地形类型区分能力分析3个角度，对各粗糙度算法进行对比，并给出各算法区分地形类型的适宜性评价。

2 结果与分析

2.1 不同地表粗糙度算法提取结果的空间格局分析

2.1.1 图像表面格局对比 11种地表粗糙度算法提取结果经极差标准化处理后(值域设为0～100)的结果如图3所示。

图3 不同地表粗糙度算法提取结果的比较Fig.3 Comparison of results extracted by different surface roughness algorithms

图3表明：(1)Slope、RMSH、Range、AS、RMSS、RMSD 6种算法提取的结果高度相似，均表现为秦巴山区粗糙度值高，黄土丘陵和川中丘陵粗糙度值居中，渭河平原和汉中平原粗糙度值低，从图3可直观地区分山地、丘陵、平原这3种地形；(2)VD、AR和γ 3种算法粗糙度数值整体较低，高值集中在秦巴山地高程急剧变化的地方，难以区分丘陵和平原，其中γ算法的结果对丘陵和平原的区分能力最差；(3)SDS和DCE 2种算法均难以区分丘陵和山地，但DCE算法在平原地区表现出比其他算法更丰富的纹理特征。

2.1.2 空间相关性 根据11种算法提取结果之间的相关性(表1)，可以将其分为2组，第1组包括Slope、RMSH、Range、AS、RMSS、RMSD、AR、γ 8种算法，这8种算法提取结果之间的相关性均高于0.88，相关性较强，其中Slope、RMSH、Range、AS、RMSS、RMSD 6种算法提取结果之间的相关性均高于0.97，相关性很高；第2组包括SDS、DCE、VD 3种算法，这3种算法与其余8种算法提取结果之间的相关性均低于0.73。

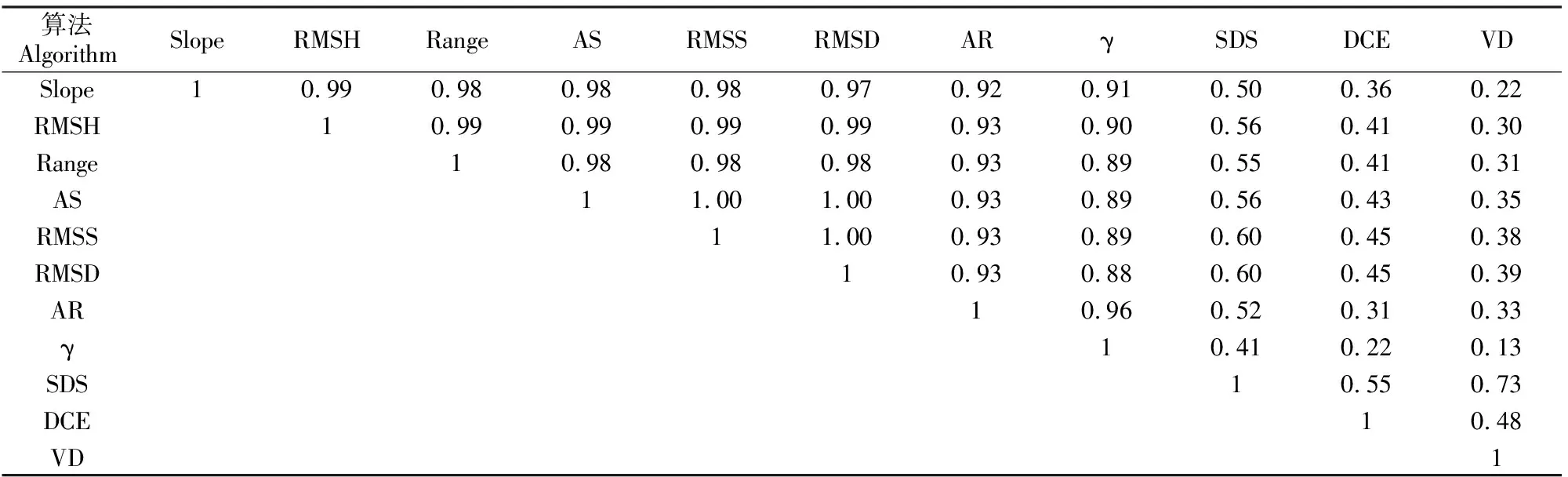
表1 不同地表粗糙度算法提取结果的相关性Table 1 Correlation of results extracted by different surface roughness algorithms

2.2 不同地表粗糙度算法提取结果的统计分布分析

统计分布是对地理数据表面值整体特征进行分析的最常用方法，本研究从统计特征值和频率分布曲线两方面对各算法进行分析。

2.2.1 统计特征值分析 极差标准化(值域设为0～100)后，不同算法提取粗糙度的统计特征值如图4所示。

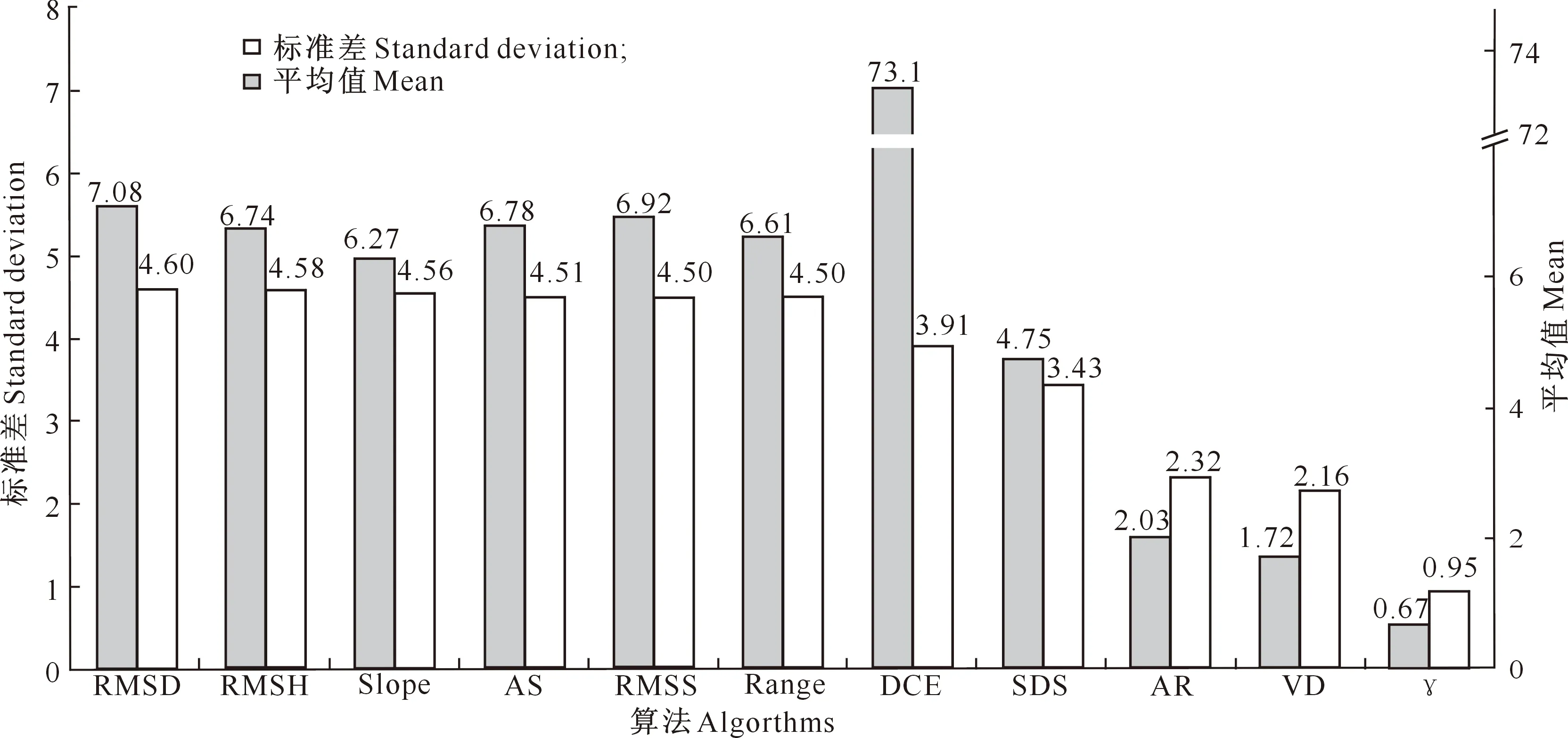
图4 不同地表粗糙度算法提取结果的统计特征值Fig.4 Arithmetic mean and STD of results extracted by different surface roughness algorithms

由图4可见：(1) Slope、RMSH、Range、RMSD、RMSS、AS 6种算法的标准差与平均值相近，与2.1节中这6种算法提取结果的空间格局相似、相关性极高的结果一致，且这6种算法的标准差高于其他算法，说明其粗糙度结果的离散程度高于其他算法，表达了更丰富的表面信息；(2) AR、VD、γ 3种算法的平均值和标准差都很低，与2.1节中这3种算法结果数值整体偏低、层次不分明的图像特征一致；(3) DCE算法的平均值最高，但标准差居中，这与其提取结果在山地和丘陵区粗糙度值均较高的特点一致;(4) SDS算法平均值与标准差均居中，与其提取结果数值整体不高，且难以区分山地和丘陵的特征一致。

2.2.2 频率分布曲线 各粗糙度结果极差标准化(值域设为0～100)后的频率分布曲线如图5所示。由图5可见：(1) Slope、RMSH、Range、RMSD、RMSS、AS 6种算法的频率曲线几乎重叠，分别在粗糙度值为0.2和5.5附近有2个波峰，SDS算法的频率曲线虽然也有2个波峰，但第2个波峰位置在粗糙度值为3.2附近；(2) DCE算法的频率曲线比较特殊，只有1个明显的波峰，且波峰对应的粗糙度集中在高值(60～80)；(3) VD、AR、γ 3种算法没有明显波峰，且粗糙度集中在低值。不同算法频率分布曲线的变化与表面值的分布特征和统计特征值变化一致。

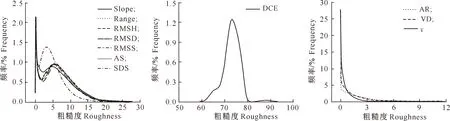
图5 不同地表粗糙度算法提取结果的频率分布曲线Fig.5 Distribution of results extracted by different surface roughness algorithms

2.3 不同地表粗糙度算法的地形类型区分能力分析

由不同算法空间格局和统计分布特征分析结果可以看出，Slope、RMSH、Range、RMSD、RMSS、AS 6种算法有较强的相似性，且对地形特征的表达都较好；DCE算法具有一定特殊性，与其他算法相比，其在平原区有更好的纹理特征。综合以上分析，且考虑到Slope和Range算法成熟且应用广泛，故选用Slope、Range和DCE 3种算法，分析其区分地形类型的能力。

2.3.1 滤波窗口选取 不同矩形窗口均值滤波损失的高频信息统计结果如图6所示。

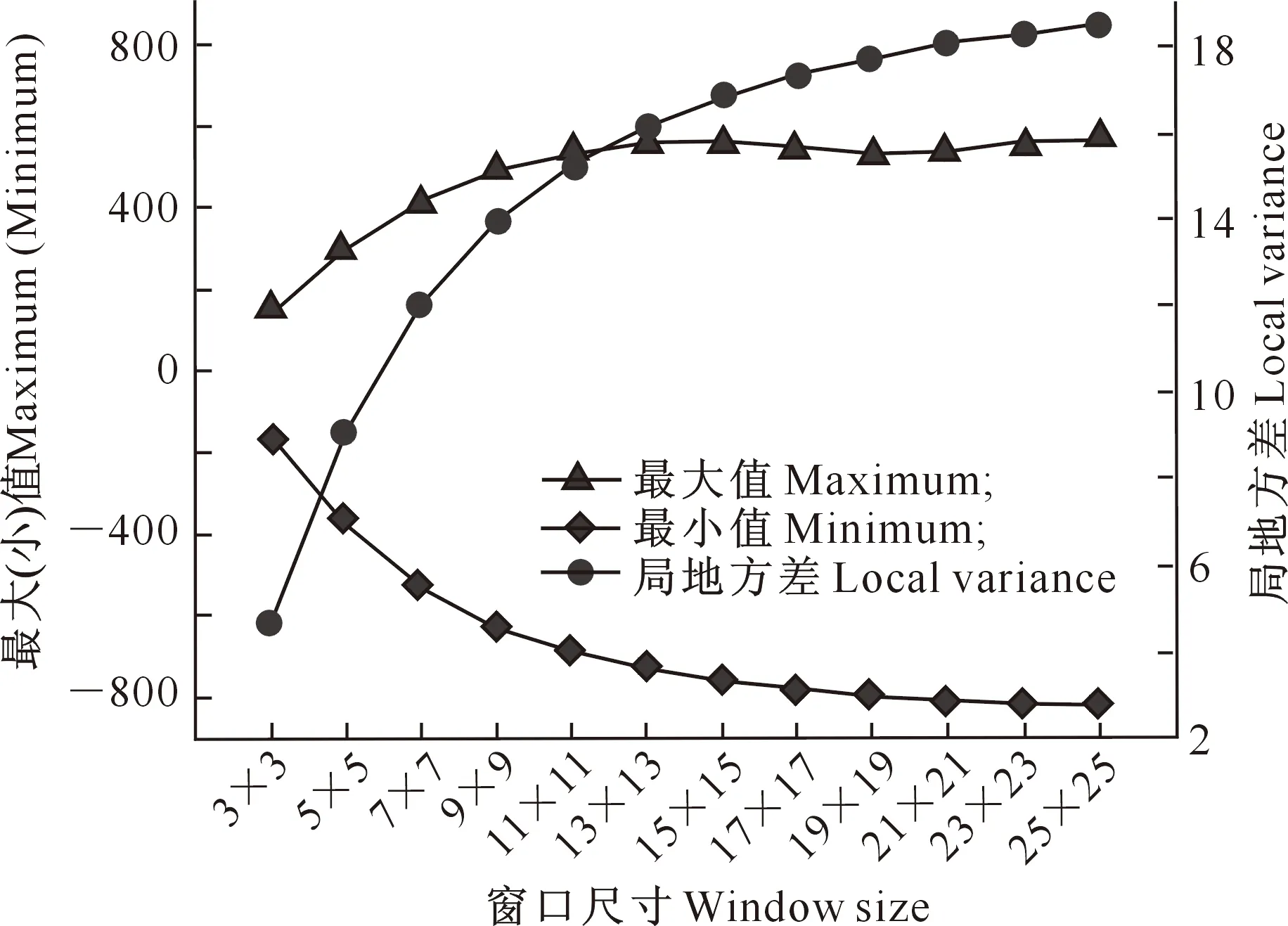
图6 不同矩形窗口均值滤波损失的高频信息统计特征值Fig.6 Maximum,minimum and local variances of high frequency information lost by mean filter of different rectangular windows

由图6可见，当矩形窗口大小达到13×13时，高频信息的最小值、最大值和局地方差基本趋于稳定，说明滤掉的高频信息不再增加，根据这一结果，本研究最终选择13×13的矩形窗口对粗糙度结果进行均值滤波。

2.3.2 典型断面分析 研究布设的断面线如图7所示，Slope、Range、DCE 3种算法滤波后的结果(值域拉伸到0～100)沿断面线的形态分布如图8所示，这3种算法滤波后的结果在不同地形区的分布情况见图9。

图7 断面线位置示意Fig.7 Location of the profile

图8 不同算法地表粗糙度滤波后结果的断面Fig.8 Profiles of different algorithms based roughness with low pass filtering

箱线图从下至上依次为频率10%,25%,50%,75%,90%的个数，十字丝代表平均值The boxplots from bottom to top refer to the frequency of 10%,25%,50%,75%,90% and the crosshairs refer to mean values

由图8和图9可以看出，Slope和Range滤波后粗糙度沿断面线的形态分布几乎重叠，3种地形对应的纵坐标分别集中在3个层次上；这2种算法在3种地形区至少80%的粗糙度值完全不相交，可以明显区分平原、丘陵、山地。DCE滤波后粗糙度的形态分布与Slope、Range不同，在平原区表现出更复杂的地表粗糙度特征，缩小了平原与丘陵的差距，丘陵与山地粗糙度值重叠度高，混淆程度大；从箱线图中也可看出，DCE方法在3种地形区粗糙度值相交程度大，说明DCE方法区分地形的能力较弱。

2.3.3 滤波后粗糙度的频率分布曲线 不同地形类型的粗糙度频率曲线呈现不同的特征，其峰值和值域范围均有较大差异。当研究区存在多种地形类型时，粗糙度频率曲线呈多峰分布。通过分析粗糙度频率曲线的波峰-波谷序列，可辨识粗糙度算法对各种地形类型的区分能力。Slope、Range和DCE 3种算法滤波后的频率曲线如图10所示。由图10可见，Slope和Range算法滤波后粗糙度结果的频率曲线相似，都有4个波峰-波谷序列，说明用这2种算法提取的粗糙度可以辨识平原、台地、丘陵和山地4种地形类型；DCE只有2个明显波峰，说明其只能辨识部分地形类型，这与2.3.2节的结果一致。

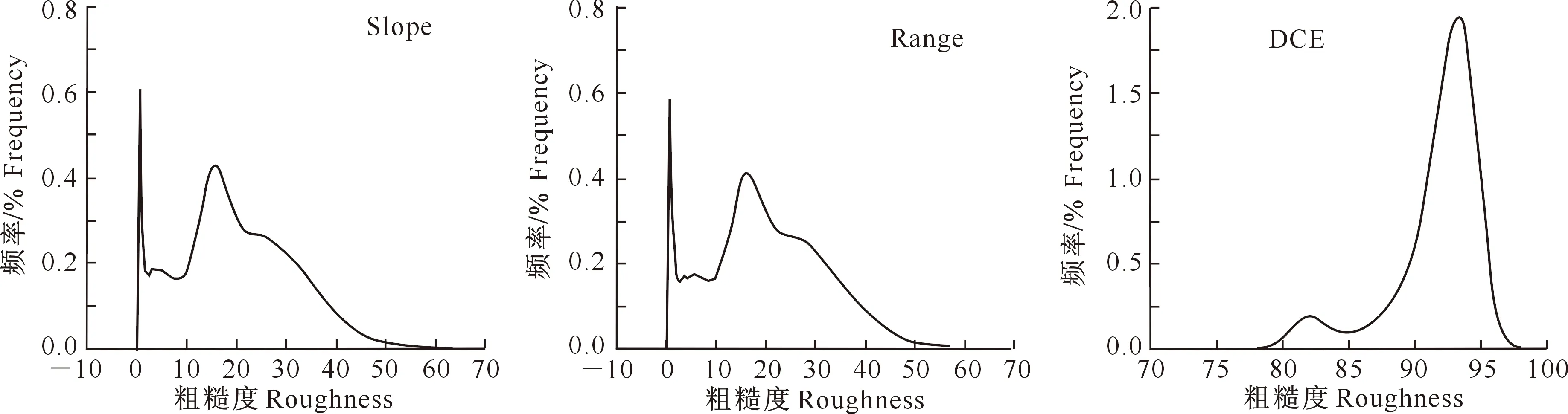
图10 不同地表粗糙度算法滤波后结果的频率分布曲线Fig.10 Results after filtering by different algorithms

3 讨 论

根据地表粗糙度算法的地理学原理，将其分为3类，包括基于高程变异性的算法、基于坡度变异性的算法和基于地表法向量的算法。

基于高程变异性的算法包括 Slope、RMSH、Range、AS、RMSS、RMSD、AR和γ。本研究中，Slope、RMSH、Range、AS、RMSS、RMSD 6种算法之间的相关性很高，在分辨率和计算窗口固定的前提下，其基本地学含义都是高差。Range、RMSH、RMSD 3种算法都是直接对窗口内像元高程的变异性进行分析得到的，其中Range是计算窗口内的最大高差，RMSH是计算窗口内的高程均方差，RMSD与RMSH相似，但只计算中心像元与边缘像元高差的均方根。RMSS和AS实质上是Slope的变形，都是根据高差与水平距离之比来计算的。因此，Slope、RMSH、Range、AS、RMSS、RMSD 6种算法在提取地表粗糙度时表现出相似的特征。AR、γ与坡度的相关性也很高，但提取效果却不如上述6种算法。AR基于比表面积(斜面面积与投影面积之比)，具体计算时AR是坡度的余弦函数，会压缩低坡度值，拉伸高坡度值，导致突出山地，模糊丘陵和平原。γ描述了移动窗口中心像元与邻域像元的相关性，地表越粗糙，地表高程值的空间差异性越大，对应的空间依赖范围越短，变异性越高。固定窗口下，AR和γ算法实质也是计算局部地表高程的高差，因此与坡度的相关性也较高。但γ计算了高差的平方，会放大地表高程变化大的地域如山地，从而导致提取结果只突出起伏较大的山区和丘陵。

基于坡度变异性的算法只有SDS，其与坡度的变化率高度相关。SDS实质为窗口像元坡度的标准差，表达了地表坡度的变异程度，这与Evans[17]、李新艳等[18]的认识一致。这一原因导致SDS算法不易区分坡度变率相似的丘陵和山地，所以在地形类型分区时，不是重点考虑的算法。

基于地表法向量的算法包括DCE和VD。这2种算法用垂直于地面的法向量在空间上的聚集程度刻画地表粗糙度，法向量越聚集，地表越平滑；越分散，地表越粗糙。这2种算法在一定程度上表达了地表坡度和坡向的局地变异，因而不适合对宏观地形类型进行划分。

本研究以地形类型划分为目的，对比分析不同地表粗糙度算法的特点，所以在认识上与已有的研究结论不完全相同。在地质灾害应用研究中，Mckean等[7]基于高分辨率地形数据，通过计算地表粗糙度来识别滑坡，认为DCE算法在局地范围内用于滑坡范围的识别，是较为适宜的。本研究则认为，DCE算法在区域尺度上进行地形类型的划分并不适宜。在区域尺度的研究中，Grohmann等[6]基于分辨率5 m DEM的分析认为，VD算法很难表达区域性地形起伏，本研究也认为VD算法未能有效划分区域尺度地形区。地貌类型制图研究中，常用起伏度(Range)来划分基本地形形态(平原、台地、丘陵和山地)[8,19-20]。本研究通过分析不同算法区分地形类型的能力，进一步认为Range是区域尺度地形类型划分的较优算法。

本研究讨论的11种算法中，除坡度算法以外，其余算法都与计算时移动窗口的尺寸有关。窗口尺寸是一个不可回避的问题，有研究对此进行过探讨，包括寻找最佳窗口[9,21]、避免窗口尺寸影响[22]等。但该问题还在探讨中，窗口尺寸对粗糙度的影响有待进一步研究。

另外，近年来更复杂的基于频谱分析的傅里叶算法[23]和小波算法[24]也被用于粗糙度的提取。Berti等[13]认为，简单算法更能用于检测滑坡信息，因此本研究中未考虑这些复杂计算方法，这些算法也有必要进一步分析探讨。

4 结 论

本研究以辨识和区分地形类型为目标，探讨了坡度(Slope)、局地高差(Range)、高程均方差(RMSH)、高程均方根偏差(RMSD)、均方根坡度(RMSS)、绝对坡度(AS)、坡度标准差(SDS)、面积比(AR)、矢量离差(VD)、余弦特征值(DCE)、二维变异性(γ)这11种地表粗糙度算法的特点及其区分地形类型的能力，可得出以下结论：

(1)Slope、Range、RMSH、RMSD、RMSS、AS 6种算法的空间格局特征和统计分布特征都极其相似，其中具有代表性的Slope和Range算法经过低通滤波消除局部高频信息后，可有效区分研究区地形类型。可以认为以Slope和Range为代表的这6种算法是表达地表粗糙程度和区分地形类型的较佳算法。

(2)AR和γ算法提取结果难以区分平原和丘陵，虽与坡度相关性较高，但因为经过非线性变化，反而不能有效反映地表粗糙度的空间变异。SDS算法表达了坡度空间变异，提取结果难以区分坡度变率相近的丘陵和山地。DCE算法提取结果虽在平原地区有更好的纹理特征，但同样难以区分丘陵和山地。VD算法提取结果在空间格局特征和统计分布特征两方面的表现最差。可以认为AR、γ、SDS、DCE、VD 5种算法都难以表达研究区地表粗糙程度的宏观变异，不能有效区分研究区的地形类型。