基于核心素养下的数学概念教学
——以《数列的概念与简单表示法》为例
浙江省义乌市义亭中学 方书英
近几年来,对于人的核心素养的培养日渐成为新一轮课程改革的深化方向。高中数学核心素养提出的具体要求有六条:数学抽象,逻辑推理,数学建模,直观想象,数学运算和数据分析。在平时的教学中,要注意对这六种能力的培养。
本文以必修五中数列的起始课《数列的概念及简单表示法》为例,浅谈核心素养下的概念教学设计。
一、新课引入
师:多媒体投影出虎刺梅、紫竹梅、迎春花、木槿、百合、波斯菊、西番莲花朵的图片,请学生说出这些花朵花瓣的数目。
生:分别是2,3,4,5,6,8,10。
师:古希腊的毕达哥拉斯学派提出“万物皆数”。据说他们发现了很多有意思的数,观察下列图形,找出这些数的规律。
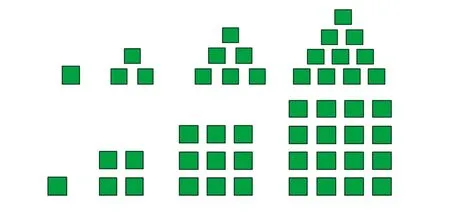
生:第一行数是1,3,6,10,15,21……
第二行数是1,4,9,10,16,25……
师:根据形状的特点,我们形象地称它们是三角形数和正方形数。
师:一般而言,兔子在出生两个月后就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔子都不死,那么一年以后可以繁殖多少对兔子?可以列出下表:
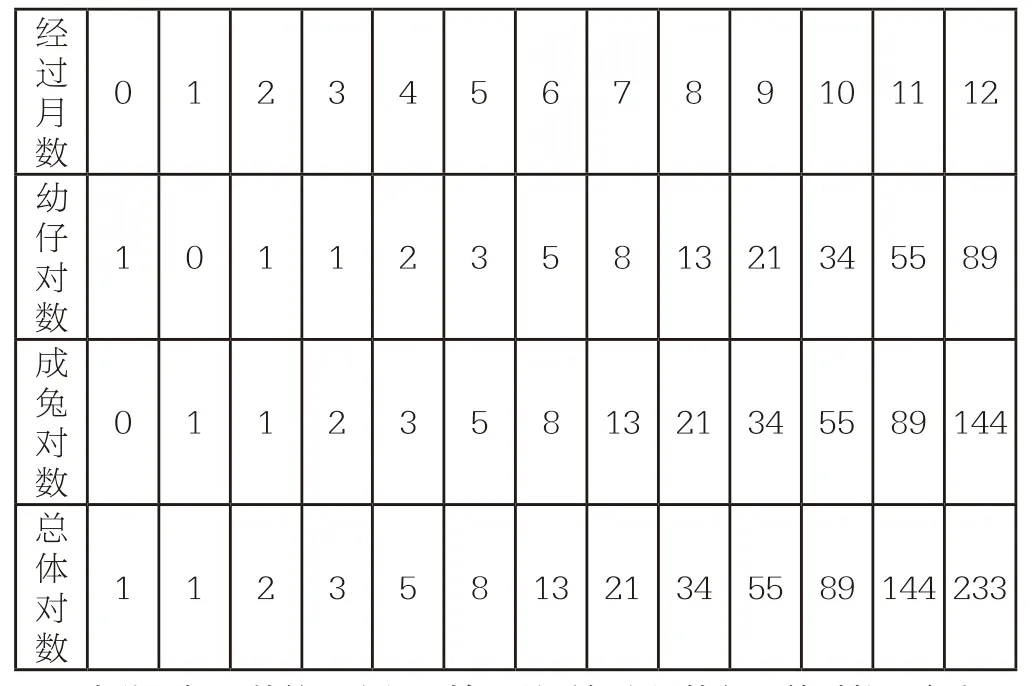
经过月0 1 2 3 4 5 6 7 8 9 10 11 12数幼仔对1 0 1 1 2 3 5 8 13 21 34 55 89数成兔对0 1 1 2 3 5 8 13 21 34 55 89 144数总体对1 1 2 3 5 8 13 21 34 55 89 144 233数
由此可知,从第一个月开始,以后每个月的兔子总对数是多少?
生:1,1,2,3,5,8,13,21,34,55,89,144,233……
师:大家记不记得这周每天我们班的出勤人数?
生:48,48,48,48,48。
师:大家能不能说出正整数的倒数各是多少?
师:1,2,3,4,…,100 除以三的余数是多少?
生:1,2,0,1,2,0,1,2,0,…,2,0,1。
【设计意图:本课开始引用生活中花瓣的数量,让美丽的花朵引起学生的兴趣,并让他们明白,在自然生活中,只要细心观察,数学无处不在。毕达哥拉斯学派的三角形和正方形数的引入,不仅是数学文化的熏陶,更是让学生通过观察三角形数和正方形数图形的特点,归纳总结出每一项数值,培养学生的逻辑推理能力和直观想象能力,也为后期引入递推公式的概念埋好伏笔,锻炼数学抽象思维能力。斐波拉契数列作为数列上的经典数列,有让学生了解一下的必要,并且形成数据表格的过程也是数学建模的过程,根据实际的兔子繁殖问题,建立数据表格,推理出斐波拉契数列的本质特点:从第三项起,每一项是前两项的和。锻炼数学抽象,逻辑推理,数学建模,数学运算,数据分析的能力。之后的问题贴近学生的日常,在教学中拉近学生与数学的亲近感。最后两个问题的设计主要是学生对已有数学知识的应用,设置得较为简单,学生基本都能解决】
二、概念生成
在投影仪上打出刚刚总结的几列数:

师:请大家观察上面这几组数学的特点?
生1:都是数。
生2:数都排成一列。
生3:这些数有顺序。
师:在黑板上板书出数列的定义:按照一定顺序排列的一列数称为数列。
师:数列1,2,3,…,40 改为3,2,1,…,40 还是不是同一个数列?
生:不是,顺序不一样,所以就不是同一组数列。
师:{1,2,3,…,40}和1,2,3,…,40 一样吗?
生:不一样,前面是集合,后面是数列。
师:那么数列和集合的概念有何区别?
生1:数列是数组成的,集合的元素不一定是数。
生2:数列有顺序,集合具有无序性。
生3:数列中数可以重复,集合中的数不能重复。
师:非常好,大家概括得很全面。
【设计意图:在新课的引入过程中,学生对这些数据的生成过程已经很熟悉,当这些数摆在面前的时候,他们自然就会对比观察出这几组数的特点,从而归纳出数列的定义。概念是越辨越明,跟熟悉的集合比较起来,学生更能深入地理解数列的特点。从具体的几组数中提炼出数列的概念,这个过程中就有对数学抽象能力、逻辑推理能力的培养】
师:集合中每一个对象,我们称为元素,那么在数列中,每一个数我们是不是也有相应的称呼呢?
生:应该也有。
师:黑板上板书:数列中的每一个数都叫这个数列的项,各项依次为第1 项(首项),第2 项,第3 项,……排在第n 位的数称为第n 项。数列中项的总数称为项数。
师:我们现在了解了数列的概念和项的概念,那么能不能用数学符号表示出来呢?
生:不知道怎么表示。
师:那大家尝试按照自己的想象来表示数列吧!在稿纸上写出来。
投影出学生的写法,方式特别多,比如:a,b,c,d,…,或A,B,C,…,或a1,a2,a3……
师:大家写得很好,都选择了用各种字母来表示数列,但如果用26 个字母表示的话,那么第27 项,28 项该怎么办呢?
生:用a1,a2,a3……可能表示无数个项。
师:非常好,大家跟数学家们想得很接近了。只是我们项数写在a 的右下方。
板书数列表示法:数列一般形式可以写成a1,a2,a3,…,an,简记{an}。
师:an和{an}有什么区别?
生:an是数学的第n 项,{an}表示整个数列。
【设计意图:对比集合中元素的定义,让学生联想到数列中的数应该也是有名称的,就很自然地给出了项的定义。其次,对于数列的数学符号表示,数学符号语言是数学抽象化的重要表征。学生自己想象出各种各样的符号,实际上就是培养了数学抽象能力,符号语言的生成更有助于学生理解数列的概念和特点】
师:我们再次观察这几组数,刚刚是找出了它们的共同特点,现在看看它们有什么区别?
2,3,4,5,6,8,10。
1,3,6,10,15,21……
1,4,9,16,25……
1,1,2,3,5,8,13,21,34,55,89,144,233……
48,48,48,48,48。
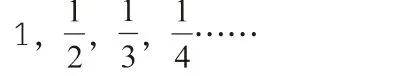
1,2,0,1,2,0,1,2,0,…,2,0,1。
生1:有的数列项的数目有限,有的无限。
生2,项的大小有的有规律,有的没有规律。
师:大小上什么规律?
生:第1,2,3 组是增大的,第4 组除了第1 项也表现出增大的,第5 组不变,第6 组减小,第七组忽大忽小。
师:非常好,我们发现从项的个数上区分,有两种,那么项数有限的我们就称为有穷数列,项数无限的我们称为无穷数列。那么从大小上区别,大家觉得怎么命名比较好?
生:越来越大的是增数列,越来越小的是减数列,不变的是常数列。师:那第7 组是什么数列?
生:不知道。
师:称为摆动数列。因此,按着数列的大小关系,我们可以分为四类:递增数列,递减数列,常数列,摆动数列。
师:观察下列几组数列:
1,2,3,4,5……
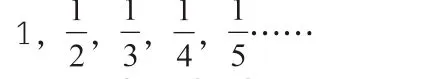
1,4,9,16,25……
这三个数列的第10 项是什么?
师:第100 项呢?
师:那么第n 项呢?
师:我们会发现这三个数列的第n 项都可以用n 表示出来。如果数列{an}的第n 项与项数之间的关系可以用一个公式来表示,那么这个公式就叫这个数列的通项公式。那么这三个数列的通项公式怎么表示?(请同学上黑板板书)
【设计意图:数列的分类标准不一样,那么所得分类也不一样,让学生自己观察,归纳,从具体问题中抽象出数列的单调性和项数特点,观察有些数列的特征,概括出每个数列的通项公式,需要学生较好的逻辑推理及数据分析能力】
师:数列1,4,9,16,……其通项公式是:an=n2,这是用通项公式表示出来,有点像函数的解析式,大家思考一下能不能够用其他的方法把这个数列表示出来?
生:可以试试表格。
师:很好,要不要上黑板试试?(学生板书)

n 1 2 3 … k …an 1 4 9 k2
师:还有吗?
生:画图。
师:好的,请问同学上黑板画画。
学生画出了一个二次函数的图像:
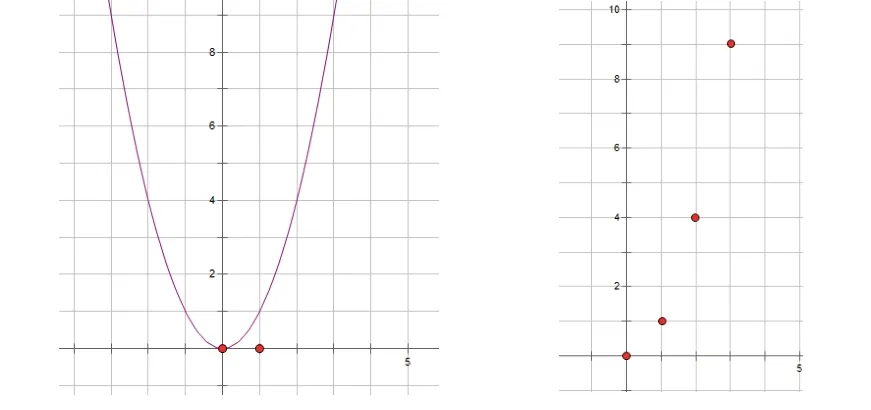
师:大家觉得这个图像有没有问题?
生:不能是连续的,应该是点。
师:重新修改学生图像如右图。
师:所以数列有三种表示方法:通项公式法,表格法,图像法。大家就会发现数列和之前学过的函数有些像,大家仔细观察下图,发现了什么?
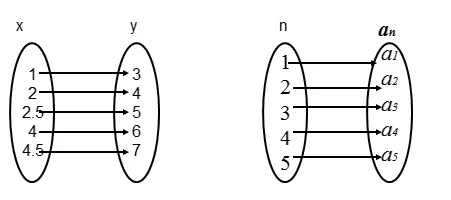
生:数列也是函数,符合函数的定义。
师:那么得到结论,数列是特殊的函数,特别之处在于定义域是正整数集(或有限子集)。
三、投影习题,并讲评习题
例1 根据下面数列的通项公式,写出它的前5 项:
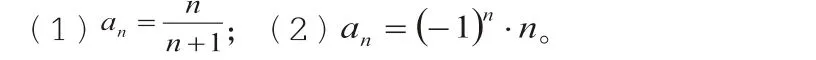
例2 写出数列的一个通项公式,使它的前4 项分别是下列各数:
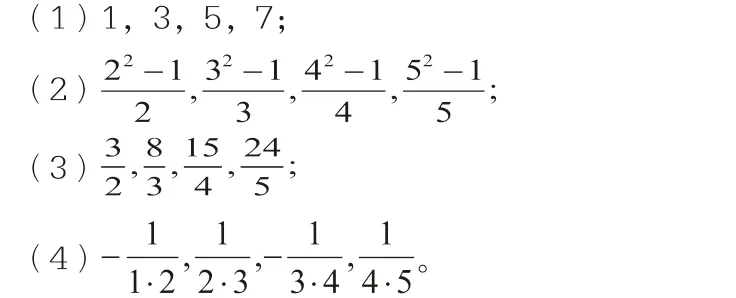
师:那么我们总结一下这节课的内容,用思维导图的形式表达出来?
【设计意图:由数列的通项公式联想到函数的解析式,进而推出数列的三种表示法,得出数列是特殊的函数。习题的设置,让学生观察数据抽象出数列的通项公式。小结用思维导图的形式总结出来,清晰简洁,体现出数学的简洁美,也更流畅地回顾了本节课的重点内容,加深了学生对本节课的理解和掌握】

