移频调制的非均匀重复转发干扰样式*

徐鹏，王振华，刘东青

(空军预警学院，湖北 武汉 430019)

0 引言

密集假目标干扰是无人机干扰系统常用的干扰样式之一[1-5]。常规的密集假目标基于数字射频存储器(digital radio frequency memory，DRFM)原理将侦收到的雷达信号进行多次延迟转发以在真实目标附近产生一系列位置随机的假目标脉冲，从而扰乱雷达对真实目标的检测[6-8]。间歇采样转发干扰是基于DRFM技术的一种新型干扰样式，其主要思想是使用信号处理中的“欠采样”原理对雷达信号进行间歇采样，将采样信号转发出去便可产生多个假目标干扰。由于这种干扰样式采用了天线收发分时工作体制，对存储容量的要求相对较低，工程实现更简单灵活[9-11]，是一种适合小型化、轻型化无人机系统的新型干扰样式。本文针对常规间歇采样转发干扰存在的问题，提出了一种在间歇采样非均匀重复转发干扰基础上进行移频调制的干扰样式。

1 常规间歇采样转发干扰

1.1 间歇采样直接转发干扰

间歇采样直接转发干扰的基本原理是当无人机侦收系统截获到雷达信号后，DRFM不失真的采样其中一小段信号后立刻处理转发，然后再采样、处理转发下一段，采样、转发分时交替工作直至脉冲信号结束[12]，其工作原理如图1所示。

由图1可知，间歇采样直接转发干扰信号可以用雷达发射信号与矩形采样脉冲的乘积来表示，矩形采样脉冲信号表示为

(1)

式中：τ为采样脉冲宽度；Ts为采样周期，且满足Ts≥2τ，采样频率fs=1/Ts。

(2)

式中：an=τfsSa(πnfsτ)。

假设截获到的雷达信号为x(t)，带宽B，时宽T。则间歇采样后的干扰信号为

xs(t)=p(t)x(t).

(3)

傅里叶变化后xs(t)的频谱为

(4)

可知，Xs(f)可以看作是X(f)的周期加权延拓，式(4)中fs为周期，即间歇采样信号可以看作是移频量为nfs的固定移频信号的幅度加权叠加，加权系数为an，如图2所示。

间歇采样直接转发干扰由于在当前采样周期内只转发一次采样信号，因此产生的假目标数目较少、幅度较低。其干扰效果受采样周期和占空比影响，主要表现在：采样周期越大，产生的主假目标距真目标越远；当采样周期一定时，占空比越大，产生的主假目标的幅值也就越大，但占空比增大的同时使得假目标距真目标较远[13]，压制干扰效果较差。

1.2 间歇采样重复转发干扰

间歇采样重复转发干扰的基本原理是当无人机干扰系统截获到一小段雷达信号后，在当前采样周期内根据系统预设程序重复转发出该小段信号，转发完成后，系统再采样下一段信号并重复转发，如此往复工作，直到截获脉冲结束。若直到截获脉冲结束时刻，当前间歇采样转发次数仍未达到规定的次数，则采用延长干扰脉冲长度的方式，将当前采样脉冲继续转发至规定的转发次数[14]。间歇采样重复转发干扰的工作原理如图3所示。

如果当前采样信号在Ts内可转发的次数最多为M，则M=Ts/τ-1，总的干扰信号可表示为

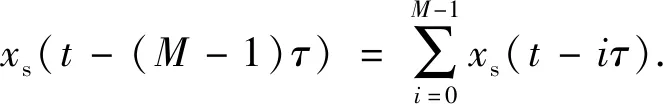
(5)

间歇采样均匀重复转发干扰技术可实现多个逼真假目标干扰，是一种应用潜力广泛的干扰样式，但其主假目标滞后真目标较远，压制干扰效果仍不理想。且在等时宽重复转发时产生的多假目标幅值恒定，要形成两侧幅度逐渐递减的假目标，还须提高干扰系统硬件设备要求以对干扰系统瞬时发射功率的大小进行调整。间歇采样非均匀重复转发可以实现对干扰信号幅值的调控，但是经过接收机脉压后仍然存在假目标距真目标较远的现象。

2 移频调制非均匀重复转发干扰

以下给出了一种基于移频调制的非均匀重复转发干扰的样式，该干扰样式可有效解决常规间歇采样干扰存在的问题，具体做法是：首先对DRFM截获到的雷达信号进行间歇采样，并对采样信号施以多普勒频移调制，然后在采样周期内进行延时非均匀转发，改变转发时宽的目的是调整干扰信号幅度。

在每个采样周期内延时转发的次数m=[Ts/τ]-1，若多普勒频移调制方式以阶梯波移频为例，其工作原理如图4所示。

假设雷达脉宽T是采样周期Ts的整数倍，采样脉宽为τ，转发时延满足td(i+1)-tdi=τ，即当前转发是在前一次转发的基础上延迟一个τ的值。转发脉宽τi的大小根据假目标幅度需要设定，阶梯波频移函数fd，式(4)可改写为

xs(t)=p(t)x(t)ej2πfdt,

(6)

式中：fd=nξ(0≤n≤[T/Ts])为移频函数。

干扰信号xs(t)第1次转发时，转发时延td1=τ，转发脉宽τ1。则第1次转发信号可表示为

ys1(t)=p′(t-τ)xs(t-τ)=
p′(t-τ)x(t-τ)ej2πfd(t-τ),

(7)

假设雷达的雷达匹配滤波器响应为h(t)，式(7)经匹配滤波处理后的输出为

Ys1(t)=h(t)*ys1(t)=h(t)*

{p′(t-τ)x(t-τ)ej2πfd(t-τ)}.

(8)

将p′(t)展开为指数形式傅里叶级数并带入式(8)，有

Ys1(t)=h(t)*{x(t-τ)ej2πfd(t-τ)·

(9)

令yf(t)=x(t-τ)*h(t)，则有

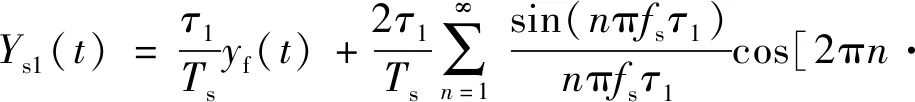
(10)

式中:yf(t)为x(t)延时τ后经匹配滤波处理后的输出。

后续转发干扰信号经匹配滤波处理后的输出依次为Ysi(t)，i=1,2,…,m。则移频调制非均匀重复转发干扰信号经匹配滤波处理后的输出可表示为

(11)

从式(11)可以看出，移频调制非均匀重复转发的干扰信号将产生一个主假目标(第1项)和主假目标两侧幅度(小于主假目标)逐渐递减的对称次假目标群(第2项)。式中第1项τiyf(t)/Ts可看作是原信号延时τ后经匹配滤波处理的输出乘上一个幅度调整因子τi/Ts所得，第2项求和式表示yf(t)经cos[2πn(ξ+fs)(t-τ)]调制后得到的加权分量，加权系数为τisin(nπfsτi)/Tsnπfsτi，调制让yf(t)的频谱搬移到采样脉冲p(t)的各次谐波n(ξ+fs)处，即产生的假目标均变成以主假目标为中心对称分布的一对假目标。设LFM信号调频斜率为K，主峰时延量Δt=[([Ts/τ]/2)-1]τ，由于移频量与延时之间存在耦合关系，故移频量的取值应根据式(12)计算：

ξ=ΔtK=[([Ts/τ]/2)-1]τK.

(12)

由式(8)，令

yfn(t)=xfn(t)*h(t)=
[x(t-τ)ej2πn(ξ+fs)(t-τ)]*h(t),

(13)

式中：yfn(t)可看作是x(t)先延时τ再频移n(ξ+fs)后经匹配滤波器后的输出响应。

不失一般性，LFM信号可表示为[15]

(14)

式中：T为脉宽;K为调频斜率，且K=B/T;B为信号带宽。

那么有

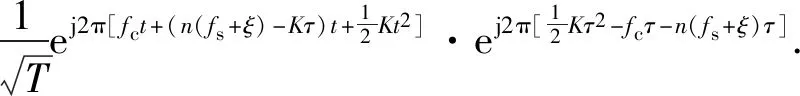
(15)

为了便于计算，取匹配滤波器的冲激响应函数为

(16)

由匹配滤波器理论知，脉压后的干扰信号yfn(t)的包络可表示为

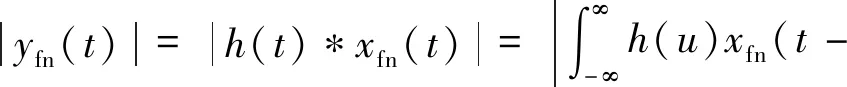
(17)

由式(17)可知，|yfn(t)|的表达形式为辛格函数形式，根据辛克函数特性知，当t=τ-n(fs+ξ)/K，yfn(t)的包络取到峰值，设2个相邻两阶峰值时间分别tx和ty，则可知出现2个相邻两阶峰值的时间间隔为

(18)

由式(18)可知，在雷达信号时宽和带宽确定后，移频调制非均匀重复转发干扰任意相邻阶假目标之间的时间间隔与采样周期和频移量大小有关。具体表现在，假目标间隔与采样周期Ts成反比，与频移量ξ成正比。也就是说，一方面间歇采样周期直接影响相邻两阶假目标之间的间隔，采样周期Ts越大，干扰信号经匹配滤波处理后形成假目标之间的间隔越小，假目标分布密集，适合实施压制性假目标干扰；Ts越小，各假目标间距大于雷达的距离分辨单元，适合对敌雷达实施欺骗性假目标干扰。另一方面频移量ξ使产生的假目标导前或滞后，假目标峰值时刻与频移量大小有关。

3 仿真与分析

3.1 干扰有效性验证实验

下面模拟雷达参数对间歇采样均匀重复转发干扰和移频调制非均匀重复转发干扰作对比仿真。

假设雷达带宽B=5 MHz，脉宽T=100 μs，所以调频斜率K=B/T，干信比取18。

实验1：采样周期Ts=40 μs，采样脉宽τ=10 μs，则采样周期内可转发的次数为m=[Ts/τ]-1=3次([·]为取整函数)，即产生3个主假目标；对于移频调制非均匀重复转发干扰，转发脉宽值依次设为6，10，6 μs。由式(12)可以计算出ξ为0.5 MHz，干扰效果如图5所示。

实验2：采样周期Ts=50 μs，采样脉宽τ=8 μs，则采样周期内可转发的次数为m=[Ts/τ]-1=5次，即产生5个主假目标；对于移频调制非均匀重复转发干扰，转发脉宽值依次设为4，6，8，6，4 μs。同理可以计算出ξ为0.8 MHz，干扰效果如图6所示。

联合图5和图6可以看出：移频调制非均匀重复转发干扰较均匀重复转发干扰而言，产生的假目标以真目标为中心、幅度由内向两侧递减，真目标被淹没在假目标群中，具有多假目标压制干扰的效果，且无需调整干扰系统发射功率就可以实现对干扰信号幅度的调控，可同时取得欺骗和群体压制干扰的双重效果。

3.2 关键参数对干扰效果的影响

为使干扰产生的假目标同时起到压制和欺骗干扰的双重效果，下面对关键参数的选取进行分析和讨论。由式(11)可知，干扰信号的干扰效果主要取决于采样脉宽、转发脉宽、采样周期和频移量的大小。

(1) 采样脉宽

由τisin(nπfsτi)/Tsnπfsτi可知，采样脉宽τ直接影响转发脉冲宽度τi的大小。对干扰效果的影响主要表现在对主次假目标的影响：一是决定次假目标群的覆盖区域，二是体现在乘数项τiyf(t)/Ts对主假目标幅值调控所占权重的大小。

仿真实验：设置雷达干信比为20，分别取不同的采样脉宽值，仿真分析采样脉宽对移频调制非均匀重复转发干扰的影响。仿真1：采样周期Ts=50 μs，采样脉宽τ=10 μs，则采样周期内可转发的次数为m=[Ts/τ]-1=4次([·]为取整函数)，即产生4个主假目标。转发脉宽值依次设为4，5，8，4 μs；仿真2：采样周期Ts=50 μs，采样脉宽τ=6 μs，则采样周期内可转发的次数为m=[Ts/τ]-1=7次，即产生7个主假目标。转发脉宽值依次设为2，3，5，6，5，3，2 μs，且根据式(12)可知ξ分别为0.75 MHz和0.9 MHz，仿真结果如图7所示。

由图7可知，τiyf(t)/Ts对主假目标幅值调控存在着无法调和的矛盾：τ越大，可转发次数越少，假目标整体幅度小，干扰有效覆盖区域变小；τ越小，可转发次数越多，干扰有效覆盖区域越大，假目标整体幅度较大，但假目标幅值衰减较快。因此需尽量减小τiyf(t)/Ts对干扰信号幅值的影响，使多普勒频移调制发挥较好的作用。

(2) 转发脉冲宽度

由式(11)可知，干扰信号幅度与转发脉冲宽度成正比，为使干扰信号起到多假目标压制干扰的效果，τi的取值应由内向外逐次递减，同时为保证转发脉冲不相互重叠，还需满足最大转发脉冲宽度τi(max)≤L/2c，L为雷达检测单元参考长度。仿真参数不变，转发脉冲宽度分别取为6，7，9，7和1，2，3，4，3，2，1 μs，结果如图8所示。

对比图7和图8可知，当采样脉宽和转发次数恒定时，转发脉冲宽度不同，其干扰效果也不同，主要表现在：假目标幅度与转发脉宽成正相关的关系，转发脉宽越大，所产生的假目标幅值越大；转发脉宽越小，假目标幅值也越小。

(3) 采样周期和移频函数

假设雷达参数和干信比不变，分别取不同的Ts和ξ，仿真分析采样周期和移频量对移频调制非均匀重复转发干扰的影响。

仿真1：取采样周期为50 μs、采样脉宽8 μs，则采样周期内可转发的次数为5次。转发脉宽值设为2，5，8，5，2 μs，ξ1为0.8 MHz，仿真结果如图9a)所示；仿真2：取采样周期20 μs、采样脉宽3 μs，则采样周期内可转发的次数5次，转发脉宽值设为1，2，3，2，1 μs，ξ2约为0.3 MHz，仿真结果如图9b)所示。

从图9b)和图9d)可以看出，采样周期不同，其干扰效果也不同。具体表现在：采样周期越大，相邻两阶假目标之间的间隔越小，分布越密集；采样周期越小，相邻两阶假目标之间的间隔越大，分布越稀疏。可以看出当采样周期越大、转发脉宽越小时(在采样周期内可转发的次数越多)，干扰密集度越大，使得τiyf(t)/Ts在幅值调控中所占的权重也就越大，但Ts的提高会加大工程实现的难度。此外，由图9a)还可以看出，由于ξ/K>2/Kτ，假目标相互独立，不会出现混叠的现象，而图9c)由于ξ/K<2/Kτ，使得假目标之间出现混叠的现象。因此，干扰需要时采样周期和移频量的大小需根据工程实现的难度和对假目标幅值调控能力进行综合考虑。

综上可得，移频调制非均匀重复转发干扰方法只需加以多普勒频移调制和控制转发脉宽值就可实现多假目标压制干扰的效果，无需改变干扰系统瞬时发射功率，降低了硬件设计的复杂程度，具有工程实现简单、同时兼有群体压制和欺骗干扰的双重效果，可为无人机干扰系统进一步提高提供理论参考。

4 结论

论文针对常规间歇采样干扰样式存在的缺点，提出了一种基于移频调制的非均匀重复转发干扰样式，该干扰样式主要有以下优势：

(1) 通过移频方式使得主假目标能够完全对准真实目标，充分利用干扰能量，达到最好的压制干扰效果。

(2) 可通过控制重复转发的脉宽来控制次假目标幅度，使得距离真实回波较远的干扰信号幅度迅速下降，能够有效的优化干扰资源配置。

(3) 根据作战任务的需要，设置合理的无人机系统参数，可以采用欺骗或压制的干扰手段实现对目标雷达的有效干扰。

(4) 采用间歇采样的方法，对无人机干扰系统的硬件设计难度要求低，易于工程实现。