基于Revised IMPROVE 方法和MIE 方法计算 北京地区气溶胶消光系数的对比分析

刘斌，臧增亮，田平，颜鹏，蔡恒明，张仁健

（1.国防科技大学 气象海洋学院，南京 211101；2.云降水物理研究和云水资源开发北京市重点 实验室中心，北京 100089；3.中国气象局气象探测中心，北京 100081；4.中国人民解放军 93220 部队，哈尔滨 150040；5.中国科学院大气物理研究所 中国科学院 东亚区域气候-环境重点实验室 北京 100029）

大气气溶胶是大气与悬浮在其中的固体和液体微粒共同组成的多相系，其吸收和散射作用对地气系统的辐射收支平衡，以及全球环境和气候都有着重要的影响[1-3]。气溶胶的散射和吸收效应可以利用消光系数来衡量，激光雷达、浊度计、能见度仪等都可以直接或间接测量气溶胶的消光系数。由于消光系数与气溶胶的浓度、化学成分、粒径分布等参数相关，也可以通过这些参数估计消光系数。常用的估计方法有基于多元回归的Interagency Monitoring of Protected Visual Environments 法（以下简称IMPROVE 方法），以及基于MIE 理论计算每个粒子的消光效率再积分求取的方法（以下简称MIE 方法）。

IMPROVE 方程是一个基于辐射传输理论、结合大量观测实验建立的不同物种质量浓度和颗粒物消光系数之间的多元线性方程，能够快速计算气溶胶的消光系数。Malm 等[4]基于IMPROVE 网络监测观测的六类物种质量浓度数据，构建了原始的IMPROVE方程（Original IMPROVE algorithm），并利用该IMPROVE 方程估计各种气溶胶化学成分对消光的贡献，为环境监测和环境治理提供了有效的数据支撑。Pitchford 等[5]发现，原始的IMPROVE 方程往往会低估消光系数的高值，高估消光系数的低值，并提出了一种修正算法（Revised IMPROVE algorithm）。Revised IMPROVE 算法使用硫酸盐、硝酸盐和有机物组分的分离组分消光效率模型，其中硫酸盐、硝酸盐和有机物按其质量浓度分为大模态和小模态，文中即采用修正的IMPROVE 方程（Revised IMPROVE algorithm）。由于Revised IMPROVE 方程形式简单，并具有良好的计算精度，在国内外得到广泛应用，朱李华[6]和Tao 等[7]计算了北京冬季、广州冬季和成都地区的气溶胶消光系数，发现该公式在我国地区具有较好的适用性，气溶胶中硫酸铵、硝酸铵和有机物消光作用贡献比重较大。

MIE 方法是1908 年米氏（Gustav Mie）通过电磁波的麦克斯韦方程的计算，得到的一个关于光散射的严格解，该方法能精确地描述任何尺度参数均匀球状粒子的散射，是计算气溶胶消光系数的经典方 法[8-11]。刘新民等[12]利用MIE 方法对北京市夏季大气散射系数进行拟合，计算结果与实际观测数据吻合较好，董海燕[13]利用MIE 方法研究了天津市夏季气溶胶的消光贡献，发现气溶胶消光主要集中于粒径小于1.00 μm 的颗粒物，消光贡献率为80%以上。

已有很多研究使用IMPROVE 方程和MIE 方法计算气溶胶消光系数，但目前使用两种方法计算大气消光系数在北京地区的对比研究方面还较少。文中将采用北京地区2012 年夏季观测的气溶胶颗粒物成分数据和消光系数实测数据，利用Revised IMPROVE方程和MIE 方法计算大气气溶胶消光系数，评估两种方法的准确性和适用性。

1 资料与方法

1.1 观测资料

膜采样的地点位于中国科学院大气物理研究所铁塔分部（39°58′N，116°22′E），位于北京市北三环和北四环之间，海拔约60 m，采样点距离院内325 m铁塔约50 m，采样点周围没有明显的污染源。于2012年6 月3 日—30 日进行了28 d 的连续观测，获得了PM2.5/PM10水溶性离子，包括五种阴离子（、、Cl-、F-、）、五种阳离子（Na+、、K+、Mg2+和Ca2+）、有机碳、元素碳等12 种观测数据，同步利用散射积分浊度计（ Aurora 3000 Intergrating Nephelometer， Ecotech， Australia）观测大气散射系数。

大气颗粒物水溶性离子的浓度是通过离子色谱测量而得到。文中所用测量离子色谱的仪器型号是 DX-500（Dionex Corp，Sunnyvale，CA），采集大气颗粒物的滤膜经过纯水萃取后配置成溶液，将溶液分别通入阴阳离子色谱中，然后根据色谱仪检测出的每个峰的位置来判断离子的种类，再通过峰面积转化得到离子的浓度[14]。

1.2 观测资料的处理

气溶胶消光系数为散射系数与吸收系数之和，由于观测数据只有散射系数，而吸收系数需要用黑碳气溶胶进行估计。潘小乐等[15]进行气溶胶吸收系数的分离研究结果表明，在中国的大部分城市，对可见光的吸收都是由黑碳气溶胶引起，吸收系数可以表示为[16]：

式中： bab为气溶胶吸收系数，(mol/L)/m；σ 为大气中分散态单位质量黑碳气溶胶的比吸收系数，对于城市地区，σ 应在7～10 之间；mbc是Aethalometer 在880 nm 波长处测量的未订正的黑碳浓度，μg/m3。

吴兑[17]基于平行对比观测得到σ 为8.28，该换算系数在国内有较好的通用性[18]。因此文中使用该拟合公式计算气溶胶吸收系数，该吸收系数与观测的散射系数相加作为实际的消光系数。

1.3 消光系数的计算方法

1）基于Revised IMPROVE 方程的消光系数计算方法。Revised IMPROVE 方程形式为：

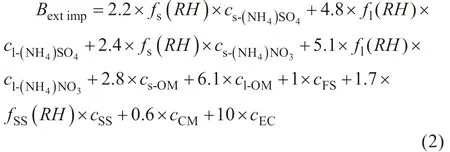
式中：Bextimp为计算的消光系数；RH 为相对湿度；f(RH)为增长因子；

对于f(RH)，一般认为样品的相对湿度在40%之下的时候，颗粒物消光系数不会随相对湿度变化。文中观测时使用的数据湿度均在40%之下，故f(RH)取值为1。另外，由于测量的是、和三种离子，它们之间并不一定能完全配成(NH4)2SO4和NH4NO3，根据三个离子浓度之间的相关性的大小，判断先与结合或与结合，估计得到(NH4)2SO4和NH4NO3的质量浓度。

2）基于MIE 的消光系数计算方法。根据MIE理论，散射光垂直于散射面和平行于散射面的两个分量的振幅函数的参数为：

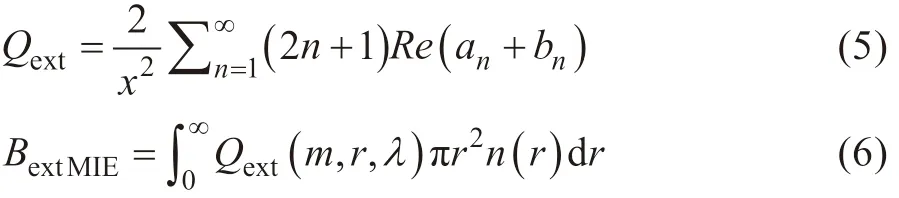
消光效率Qext表示粒子消光截面与其几何截面之比。当气溶胶粒子复折射率m 有虚部的时候，存在吸收作用，Qext随颗粒物直径d 的变化规律如图1 所示。

图1 Q ext 随颗粒物直径d 的变化规律

由式（6）可知，消光系数BextMIE是复折射指数m、粒子半径r 和d r 粒径范围内粒子数量之间的函数关系，其中粒子数谱n(r)可以由体积谱进行计算，体积谱的分布采用如下两种假设。

方案A 基于PM10总量双峰态假设的MIE 计算

假设气溶胶体积谱分布为双峰型。根据对北京夏季布点采样来描述中国北方大气气溶胶体积谱分布特征的相关研究，得出北京地区气溶胶体积谱在0.1～0.3 μm 之间出现第一峰，在4.5～7.0 μm 之间又会清晰地出现第二个峰[20]，如图2 所示。由于已知粗细两个粒径段内气溶胶总量，利用各自的几何平均粒径、标准偏差共4 个参数就可以确定体积谱的分布。

气溶胶粒子的双峰体积谱分布用式（7）描述：

式中： 1V 、 2V 、g1D 、g2D 、g1σ 、g2σ 分别为气溶胶粗、细粒径段总体积、几何平均粒径和几何标准偏差；D 为干气溶胶粒子的粒径。通过式（7）可以将粗细两个粒径段的总体积在D 范围内展开，并细化为各个粒径段，进而求出各个粒径段内的气溶胶体积，进一步算出粒子数谱n(r)，即可利用式（6）计算出消光系数。

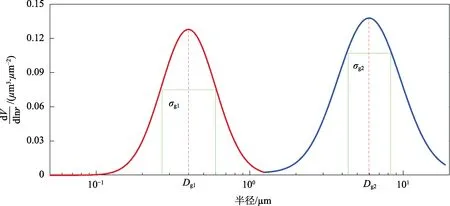
图2 北京地区夏季气溶胶粒子体积谱分布

气溶胶折射率m 的取值采用内混合假设中的均匀混合模型（黑碳为核，其他颗粒物为壳）[21]，一般是用体平均法求解其折射率，即除BC 之外其他6 种粒子的折射率为mshell：

方案B 基于化学组分体积谱分布假设的MIE 计算

由于夏季北京气溶胶各个组分的复折射指数和体积谱分布并不相同，用方案A 计算只能采用平均的复折射指数，忽略了各成分的特性，因此在方案B中考虑PM10所有12 种化学组分的体积谱分布，分别进行MIE 计算之后求和得到消光系数。其中、、、K+、EC、OC 采用单峰分布，峰值粒径为0.54～1.0 μm。Cl-、Na+采用双峰分布，峰值粒径为0.54～1.0 μm 和3.2～5.6 μm，Mg2+、Ca2+采用单峰分布，峰值粒径为3.2～5.6 μm[22]。方案中、、、K+、EC、OC 谱分布参数设置与Cl-、Na+双峰谱的细粒径段参数（Dg1、σg1）一致，Mg2+、Ca2+谱分布参数设置与Cl¯、Na+双峰谱的粗粒径段参数（Dg2、σg2）一致。各组分的密度和复折射指数采用刘新民文献 数据[12]。

1.4 对比检验方法

为了分析上面三种方法计算出来的消光系数与实际结果的一致性，建立了如下回归方程进行评估：

式中：Bext为实际消光系数，即观测的散射系数与黑碳的吸收系数之和；Bextcal为采用 Revised IMPROVE 方程或MIE 方法计算的消光系数。回归方程的相关系数为R，当K 和R 都接近1 时，表示回归效果较好，计算结果与实际结果相一致。

利用MIE 方法两种方案计算消光系数时，由于只有PM10 和各组分质量浓度，而粗细粒径段的Dg1、σg1、Dg2、σg2这4 个参数仍是未知的，对粗细粒径Dg1、Dg2分别在0.1～2.0 μm、2.0～10 μm，σg1、σg2在1.0～2.0 μm 范围内循环取值，尝试找到最优的参数值。为寻找最优的拟合参数，定义最优化指数Y：

Y 取最小值表示K 和R 都接近于1，从而可以得到对应粗细粒子各自几何平均粒径和几何标准偏差共4 个参数。

2 结果与分析

观测的散射系数与由式（1）计算的吸收系数如图1 所示，可以看出，两者相差1 个量级以上。这是因为观测的黑碳质量浓度较低，所以两者之和作为实际的消光系数主要由散射系数决定。

2.1 基于Revised IMPROVE 方法的消光系数计算结果分析

图4 为基于Revised IMPROVE 方程计算的消光系数Bextimp和实际观测的消光系数Bextobs的散点图。由图4 可知，Bextimp和Bextobs的相关系数R 达到了0.952，这说明Revised IMPROVE 方程估计的气溶胶消光系数与实际相一致，该方法对北京地区夏季的气溶胶消光系数的估算较为准确。

2.2 基于 MIE 方法的消光系数计算结果 分析

基于MIE 方法计算消光系数时，需要对Dg1、σg1、Dg2、σg2这4 个参数进行循环试验，以确定最优的Y值。经过循环试验，得到两个方案最优化指数 最小值对应的4 个参数见表1。

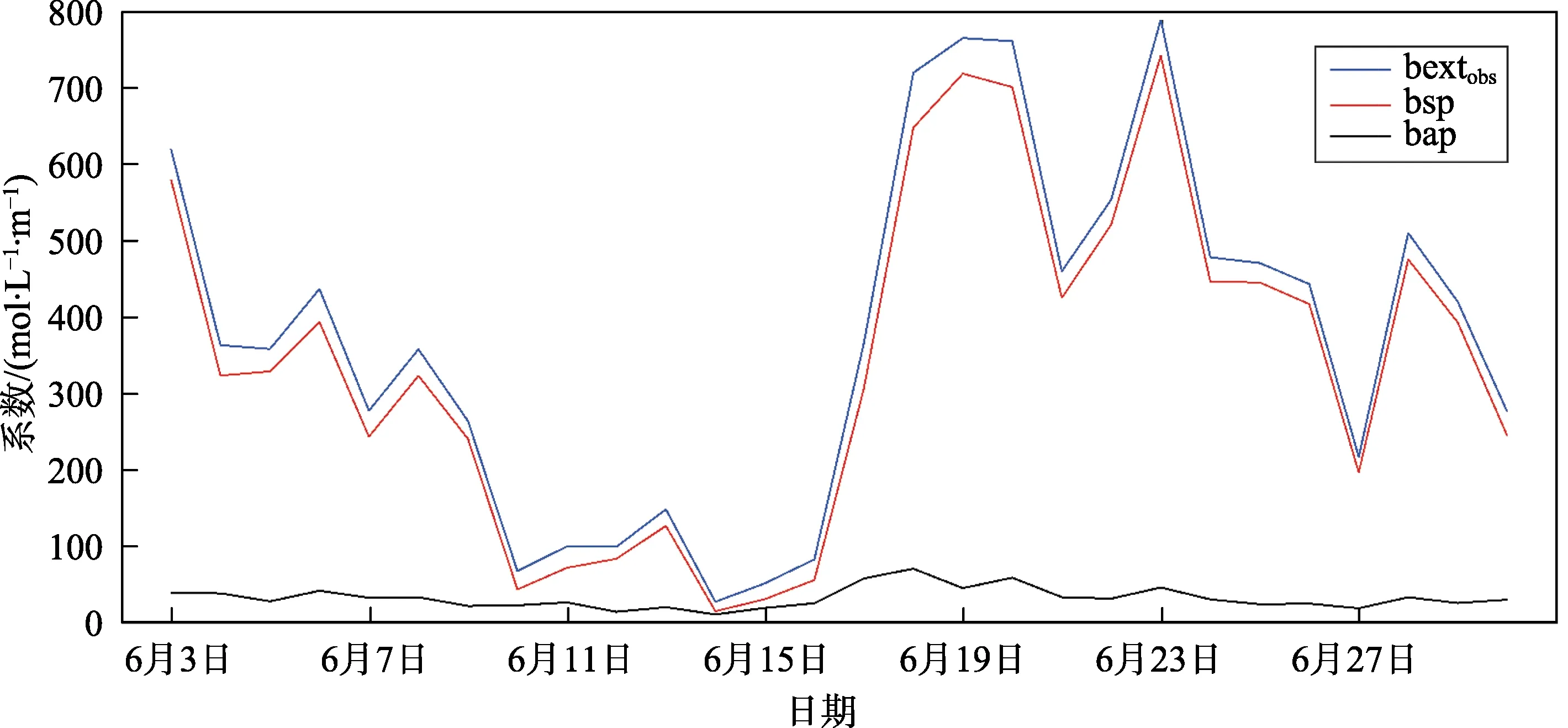
图3 观测消光系数、观测散射系数和黑碳的消光系数逐日变化趋势

图4 Revised IMPROVE 方程计算消光系数与观测 消光系数相关性散点图

方案A 中颗粒物体积谱粒径参数稍大于经验观测结果，原因可能是由于方案A 复折射指数采用平均值（1.49+0.0004i），由于相较于各组分计算的消光 效率偏小，细颗粒物的峰值偏大，可以使消光效率增大，并接近于第一个峰值，弥补复折射指数偏小的效 应。方案B 中细颗粒谱几何平均粒径为0.48 μm，粗粒径为6 μm，基本与经验观测结果一致。

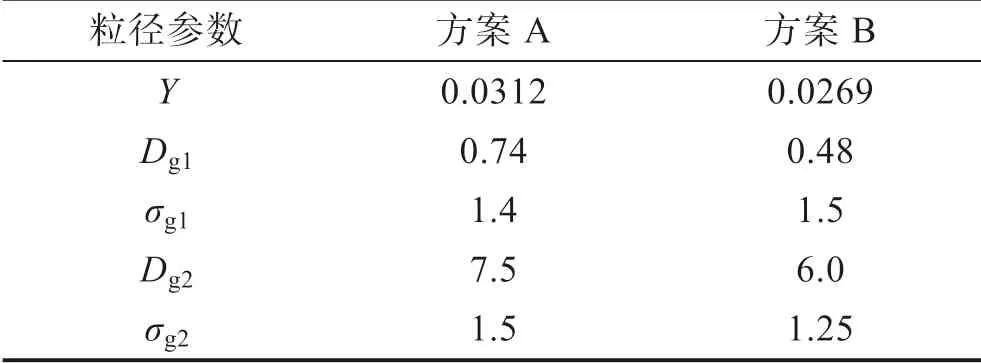
表1 两种方案最优化指数最小值对应的4 个粒径参数 μm

图5 为基于判断参数筛选的两种谱分布方案进行MIE 方法计算的BextMIE与观测消光系数Bextobs相关性的散点图。可以看出，计算结果能较好地拟合出北京市夏季消光系数，相比于 Revised IMPROVE 方程，MIE 计算结果数据相关性更好，方案A 和方案B 的斜率K 均为1.00，其中针对各组分的谱分布分别进行MIE 计算的相关系数R 略高，达到了0.9734。

图5 两种方案下MIE 方法计算B ext MIE 的与观测消光系数B ext obs 相关性散点图

3 结论

1）基于Revised IMPROVE 方程计算了大气消光系数，计算值Bextimp和实测值Bextobs的相关系数为0.952，说明该方程适用于北京夏季大气消光系数的解析。

2）通过定义最优化指数，经MIE 计算筛选出最小值对应的气溶胶谱分布参数，其中总量双峰分布体积谱方案（方案A）的细颗粒谱几何平均粒径为0.74 μm，粗粒径为7.5μm。基于化学组分体积谱方案（方案B）的细颗粒谱几何平均粒径为0.48 μm，粗粒径为6 μm，与粒径谱的观测结果一致。

3）基于MIE 方法方案A 和方案B 计算的大气消光系数，与实际值的相关系数分别为 0.9686 和0.9734，说明MIE 方法能较好地计算北京夏季大气消光系数，其中基于化学组分体积谱的准确性最高。