高斯伪谱法在变推力导弹弹道优化中的应用*
李怡昕,李旭,刘少波,康鹏
(北京电子工程总体研究所,北京 100854)
0 引言
推力可调固体火箭发动机可根据作战任务、作战平台实时调节推力大小,实现推进剂能量的合理分配,从而实现武器装备作战能力多样化,因而成为固体火箭发动机发展的趋势[1]。
国外已在推力可控固体火箭发动机的应用方面取得一些进展。美国Aerojet公司的EIHAWK导弹集成了喉栓式推力可调喷管,在装药量一定的条件下成功实现导弹增程。美陆军精确攻击导弹PAM采用了Aerojet公司的喉栓式变推力发动机,可根据任务目标实时调节推力,从而扩大作战范围,且在2007~2009年间,成功进行多次飞行试验,展示出固体发动机推力可调技术的可行性[2]。
近年来,国内外学者对于伪谱法用于最优控制问题的应用研究愈加广泛,发展愈加成熟,而飞行器轨迹优化中的伪谱法应用研究是伪谱法应用最成功的领域之一。
目前,伪谱法在飞行器轨迹优化中的应用已取得相当可观的成果。其中,Legendre伪谱法已被应用于解决运载火箭上升段轨迹快速优化问题[3]、通用航空飞行器性能优化问题[4]、航天飞机应急下降轨迹优化问题[5]、航天器最优转移轨道问题[6]、月球软着陆轨迹快速优化问题[7];Gauss伪谱法已被应用于解决小推力航天器轨迹优化问题和Delta运载火箭上升段轨迹优化问题[8]、日-火Halo转移轨道快速优化设计问题[9]、多级固体运载火箭上升段轨迹快速优化问题[10]、空空导弹最优中制导律设计中的应用问题[11];月球软着陆轨道优化中的应用问题[12]、高超声速飞行器的轨迹优化问题[13]。总的来说,国内外对于伪谱法在飞行器轨迹优化设计中的应用正处于快速发展向逐步成熟的迈进阶段[14]。
针对拦截近程目标,本文采用变推力控制,选用固体火箭发动机实现推力可调,提出考虑末速最大的目标函数,给出相应的约束条件,并使用高斯伪谱法进行弹道优化设计,最后给出相应的仿真校验结果。其中,选用的变推力固体火箭发动机推进剂质量给定,可根据实际需要调节推力大小。本文将高斯伪谱法应用于处理可变推力近程导弹弹道优化设计,在推进剂一定的条件下考虑合理分配能量,提出了一种设计变推力弹道的新思路。
1 建立高斯伪谱优化模型
1.1 导弹运动学模型
本文作如下假设:导弹在整个飞行期间都处于瞬时平衡状态;导弹绕弹体轴的转动是无惯性的;导弹的控制系统理想工作,无误差,无时间延迟。
导弹在铅垂平面内的运动方程组可以简化为
(1)
式中:m为导弹质量;v为速度;FY为升力;FX为阻力;G为重力;P为推力;α为攻角;θ为弹道倾角;重力加速度g=9.81 m/s2。
改写成状态方程的形式
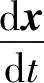
(2)
式中:状态变量x=(v,θ,x,y,m)T;控制变量u=(P,α)T;t0为初始时刻;tf为末端时刻。
1.2 基于高斯伪谱法的离散表示
Gauss伪谱法实质上是一种离散变量表示法,其核心在于将状态变量和控制变量在高斯点上离散,并以离散点为节点构造Lagrange插值多项式逼近原连续函数。下面将利用高斯伪谱法完成系统微分方程式(2)到代数方程式(11)的转化[15]:
首先,将原系统的状态方程式(2)做时域变换
(3)
将原时间区间t∈[t0,tf]映射到τ∈[-1,1],则变换后的最优控制问题状态方程为
(4)
性能指标、边界条件、不等式约束为
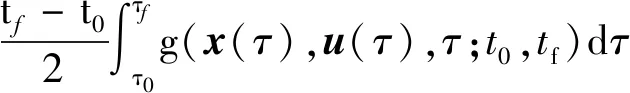
(5)
Φ(x(τ0),t0,x(τf),tf)=0,
(6)
C(x(τ),u(τ),τ;t0,tf)≤0,τ∈[-1,1],
(7)
式中:容许控制u(τ)∈U;τ∈[-1,1]。
其次,在区间τ∈[-1,1)内选取Gauss点τk(k=1,2,…,N)作为节点构造Lagrange多项式逼近原连续状态变量x(τ)和控制变量u(τ),即离散化为
(8)
(9)

记Xk=X(τk)=x(τk),Uk=U(τk)=u(τk)。式(8)对时间求导则有
(10)
式中:D∈RN∧(N+1)为微分矩阵,从而系统微分方程式(2)转化为代数约束:
(11)
式中:k=1,2,…,N。
原性能指标、边界条件和不等式约束式(5)到式(7)可离散表示为
(12)
Φ(X0,t0,Xf,tf)=0,
(13)
C(Xk,Uk,τk;t0,tf)≤0,
(14)
式中:ωk为高斯权重系数;k=1,2,…,N。
至此,原最优控制问题最终转化为非线性规划问题,式(11)到式(14)定义的非线性规划问题的解就是原最优控制问题的近似解[16]。转换所得NLP问题采用序列二次规划(SQP)方法求解。
2 弹道优化方案设计
本文以近距导弹拦截目标为特定研究背景,在推进剂质量给定的情况下采用Gauss伪谱法进行弹道优化设计,考虑选取J=vf末速最大为优化目标函数,旨在提高其末端过载能力。
2.1 发动机方案
为了进一步验证推力可调的弹道性能,本节给出变推力发动机的主要参数,且将在此基础上用高斯伪谱法进行弹道优化设计并与传统推力形式的弹道作比较和分析。
给出某变推力发动机参数见表1,推力调节范围500 N~15 kN。
可控推力固体火箭发动机的技术途径包括调节喷管喉部面积、实时改变推进剂燃速、加质发动机、胶状推进剂发动机等,其中喉部面积可调的方案理论和试验基础好,能够实现推力大小无级调节[1]。
2.2 优化模型
状态方程(2)中,状态变量x=(v,θ,x,y,m)T、控制变量u=(P,α)T为未知量,即需按一定的制导规律生成制导指令。即原运动方程联立控制方程则方程组封闭,给出相应的初始条件即可求解。
本节提出一种高斯伪谱法的优化模型,以J=vf最大为目标函数,约束条件为攻角约束-40°≤α≤40°和法向过载约束-60≤ny≤60,选取u=(P)作为待优化控制变量,由比例导引给出α值。
比例导引给出α值的原理如下:
第1步:由比例导引
(15)
给出N个高斯点τk(k=1,2,…,N)上的过载指令;
第2步:根据预先设定的状态变量、控制变量猜测区间将状态变量、控制变量在各高斯点τk(k=1,2,…,N)上初始化,即此时各高斯点上x=(v,θ,x,y,m)T,u=(P)为一系列确定值;
第3步:由动力学方程
ny=
(16)
得出各高斯点上的一系列α值。
随着高斯伪谱法优化的逐步进行,α值同步更新,该最优控制问题可以求解。
3 仿真校验
导弹初始状态x0=0,y0=10 km,v0=400 m/s,满载质量mfull=82.3 kg,空载质量memp=55 kg。
仿真图中*号各点为高斯伪谱法优化得到的离散状态量/控制量,另将高斯伪谱法得到的P,α作为输入进行数值积分,其结果用细实线表示,以验证高斯伪谱法优化结果的正确性。
3.1 发动机方案对比
目标设定为(xt,yt)=(5,12) km定点目标,导弹发射角θ=90°。
首先在表1给出的发动机参数的基础上,给定几组工程常用推力比,通过仿真计算其在比例导引下的弹道,并比较末速如表2所示,仿真结果见图1。

表2 传统发动机参数Table 2 Parameters of traditional engines

图1 传统发动机方案的弹道仿真Fig.1 Trajectory simulation of traditional engine schemes
由表2可知,近距目标考察末速最大时推力比1∶1性能最优(末速最大),将其与高斯伪谱法优化所得的变推力方案作对比,给出仿真结果如图2所示。
分析仿真结果可知,对比最佳的传统发动机方案比例导引弹道,推力可调的发动机方案下,以末速最大为优化目标,高斯伪谱法优化得到的弹道末速提升9.97%,表明采用变推力控制可显著提升导弹的弹道性能,对比结果见表3。

图2 两种发动机方案的弹道仿真Fig.2 Trajectory simulation of two engine schemes

表3 2种发动机方案的性能Table 3 Trajectory performance comparison of two engine schemes
由图2可看出,高斯伪谱法优化结果与数值积分结果有一定误差,这是由于高斯伪谱法给出的最优解为离散值,由式(9)可知,最优控制变量应以这些离散点作为节点构造Lagrange插值多项式来逼近。而细实线表示的曲线则是在离散推力值的基础上线性插值作为输入量进行数值积分的结果,因此在推力值波动较大时,二者出现误差。
3.2 有效性验证
为进一步验证高斯伪谱法应用于可变推力导弹弹道优化的有效性,本节考虑近程导弹全向发射情况,选用比例导引控制变量u=(P)的高斯伪谱法优化方案,在表1给出的推力可调发动机参数的基础上进行弹道仿真。
目标设定为(xt,yt)=(5,12) km定点目标,选取导弹发射角θ=0°,30°,…,150°,同3.1节给出推力可调与最优传统推力的弹道性能对比结果见表4。

表4 全向发射两种发动机方案的性能Table 4 Trajectory performance comparison of two omnidirectional attack engine schemes
高斯伪谱法给出导弹在不同的发射角θ=0°,30°,…,150°下的变推力弹道优化结果如图3所示,高斯伪谱法优化得到的弹道末速分别提升1.67%,1.25%,2.92%,9.97%,30.44%,35.91%。区别于传统推力方案,图3d)推力曲线图体现出可变推力控制下的推力形式多样性,说明了高斯伪谱法应用于可变推力导弹弹道优化设计的可行性和有效性。
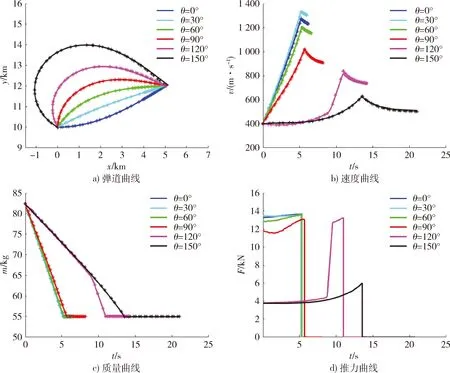
图3 全向攻击弹道仿真Fig.3 Trajectory simulation of omnidirectional attack
4 结束语
对于可变推力导弹弹道优化问题,本文提出基于比例导引的变推力导弹弹道优化模型,研究在推进剂质量给定的条件下进行能量的合理分配。仿真结果表明了高斯伪谱法应用于可变推力导弹弹道优化设计的有效性。本文采用比例导引给出制导指令,总体计算量小,可以实时在线运行。后续将对打击中远程目标及机动目标的情况进行研究,同时考虑采用hp-自适应方法对其进行改进,逐步细化网格并提高基函数阶次以获得更高的精度。

