Verification and validation of detonation modeling

Xiao Liang , Rui-li Wang

a Institute of Applied Physics and Computational Mathematics, Beijing,100094, China

b College of Mathematics and Information Science, Shandong University of Science and Technology, Qingdao, 266590, China

Keywords:Verification and validation Detonation Equation of state Detonation diffraction Reaction rate law

A B S T R A C T

1. Introduction

This article is concerned with verification and validation of simulation software for detonation phenomenon. As we all know,detonation plays as an important role in the technological field such as blasting engineering, weapon design and explosive driven device. In general, the detonation wave is a shock wave that proceeds with sustained release of the energy through the chemical reaction behind the wave.But this wave is a very complex physicalchemical phenomenon which occurs in the tiny time length and very small space width. The magnitudes of detonation speed, reaction zone, reaction time and peak pressure are o(1000 m/s),o(10-3m),o(10-6s),o(102Gpa)respectively[1-4].In some extreme situation such as nuclear explosion and Core-Collapse Supernovae(CCSNe), the pressure maybe even higher [5,6].

In order to interpret this phenomena correctly, several approaches are used to study it. Numerical simulation technique,along with theory analysis and physical experiment are regarded as three main pillars of detonation research.And each of these pillars has its own unique strength and weakness.Experiment can provide a direct research method into the physical mechanisms of this phenomenon. However due to the complexity and coupling effect between this multi-physical phenomena, it is often a challenge to design appropriate experiment that can accurately describe the behavior of this physical process, sometimes impossible. Furthermore,owing to the cost and risk of conducting specific experiment,such that it is unpractical to carry out a large number of detonation experiments. So the experimental data is usually scarce and the whole scene of mathematical-physics model for detonation cannot be reproduced in the laboratory due to above reasons.On the other hand,theoretical analysis also has its own shortage in studying the realistic detonation, especially in multi-phase flow, thermodynamic problem as well as chemical reaction mechanism.

Numerical simulation is welcomed by the community of engineering due to its low cost and repeatability. However, there are still many difficulties associated with this technique. On one hand, detonation model is usually described by highly nonlinear partial differential equations, it is difficult to find the exact analytical solution to these mathematical models[1,2,7-9].On the other hand, due to the complexity of the reality, the physical modeling and the numerical method always involves simplification of the physical reality, numerical approximation, as well as too much modeling assumption.The scholars are often puzzled by the reliability and credibility of the simulation software and its adaptability to practical application owing to above reasons. This problem greatly hinders the development and application of the numerical simulation technology.

Verification, validation and uncertainty quantification(V&V&UQ) combines strength of the physical experiment and numerical simulation;it is used to develop higher fidelity simulation software.The scientific and engineering field makes more demand on the V&V&UQ, it becomes a universal technique. V&V&UQ has become an important research direction in the engineering technology such as nuclear science and aeronautic field [10-14].Meanwhile, Advanced Simulation and Computing (ASC) program sponsored by the DoE aims at improving the predictive accuracy of the simulation software.

Many scholars have studied the V&V of detonation modeling.C.Romick, T. Aslam, J. Powers have studied the V&V of unsteady dynamics of viscous hydro-air detonation[15].J.Bdzil and D.Stewart have discussed the V&V of detonation in explosive, in which the verification is conducted by the direct numerical simulation(DNS)[16].C.Paderson,B.Brown,N.Morgan use the Sedov blast wave as a radial piston verification test [17]. C. Scovel and R. Menikoff presents the systematic approach to V&V of high explosive burn models [18].

However after a scrutiny scan of the literatures of V&V,we find that there is little article about V&V of detonation modeling when compared with other fields. The reason may be that V&V of detonationmodelingdoes not fit thestandard formatof V&V[1,2,18].First of all,the burn rate,even the equation of state(EOS)of the explosive are phenomenological and empirical,they do not have any physical meaning.So some parameters cannot be obtained by the experiment directly.In real application,some model parameters are derived by comparing the simulated result with specific experimental data.It's difficult to prevent the possibility of adjusting parameters in the model deliberately to obtain the best agreement with experimental data in this case.By the way,there is no standard experiment suited for all detonation problems. Secondly, it is difficult to describe the detonation phenomenon quantitatively since the measurement result of detonation is often given in the form of a photo.Thirdly,in some situation, different detonation products correspond to the same EOS and burn rate.In another situation,different EOS and burn rate maybeusedforthesameexplosive indifferenttest.Inaword,itis impossible to obtain a general model suited for dozens of explosive.In another word,the model form is uncertain in the detonation.Last but not least, dozens of uncertain factors exist in the detonation modeling, which greatly affect the output of the nonlinear system.Some uncertainty is caused by the inherent variation of energetic material,suchasdensity.Anotheriscausedby themeasuringmethod such as detonation velocity. There are also some uncertain factors caused by the lack of knowledge for this complex phenomenon,such astheparametersintheburnrateandsomeEOS.Soitisa challengeto carry out V&V of detonation system and it is necessary to alter the procedure of V&V in some cases.

We have developed detonation software named LAD2D. It is self-developed computational software,which aims at studying the behavior of detonation system. The simulation of this paper is based on this software.

2. V&V& UQ methodology and basic structure of LAD2D

2.1. V&V&UQ methodology

V&V technique stems from the United States, it was formally proposed by the Society for Computer Simulation(SCS)in 1979[19].Then other communities such as IEEE, DoD, AIAA, and ASME also publish their definitions of V&V from different perspective[20-23].Generally,V&V uses the scientific methods,standard procedure,and professional algorithm to verify and validate the model in order to provide evidence for computer code correctness and improve the credibility of the simulation result. Verification, which is based on the scientific reasoning, concerns the discreteness of the equation(equation and scheme),implementation of the program(code and algorithm), as well as the customer's requirement on the software(numerical simulation).Validation is built on the concept of quantitative accuracy assessment,which deals with the model form and the parameter adaptation, accuracy assessment of physical reality,the predictive accuracy of a model. It stresses the comparison between physical experiment and computational result.

Verification in this paper includes symmetry verification, conservation verification, theoretical verification, code verification,and man manufactured solution.Validation is conducted by model accuracy assessment.

UQ is a process of identifying and characterizing the input uncertainty of system, surroundings, environments, scenarios, and quantifying the propagation of input uncertainty, calculating the uncertainty of system response quantities of interest. It mainly considers how some factors affect the accuracy of the computational results and impact the confidence in predictions from the model. A large number of UQ methods are proposed in the modeling and simulation (M&S) of complex systems. We summarize various sources and methods of UQ, for detailed information,please see Fig.1.For detailed information about sensitivity analysis,surrogate model, polynomial chaos, stochastic differential equations,P-box,Dempster-Shafer theory and their applications,please see our previous paper [5,6,24-26].

2.2. Physical modeling of explosive detonation

The V&V activity cannot be implemented unless we fully understand the mathematical modeling of physics, computational geometry, as well as basic structure of the detonation. The dynamical and thermal behavior of explosive detonation is governed by a coupling of compressible Euler equation, equation of state (EOS), as well as reaction rate law, which describes the conservation of mass, momentum, and energy, chemical reaction and thermal behavior of the high explosive [1,15,16,27]. This set of equations can be written in the Lagrangian coordinate as follows

where ρ , u , P , E , e ,denote the density, velocity vector, pressure,total energy and internal energy respectively, with E =e+12 u·u denotes the kinetic energy,and v=1/ρ is the specific volume.∇denotes the divergence operator.+u·∇is the material derivative. P =P（ρ,e,F） is often called the equation of state (EOS).0 ≤F ≤1 is reaction progress variable (F =0 for unreacted material, 0 ＜F ＜1 for reacting, F =1 for completely reacted material).

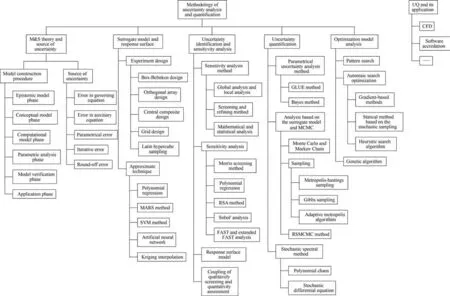
Fig.1. Uncertainty quantification methods in the complex engineering M&S.

We must point out that there are some shortages associated with the detonation modeling.Firstly,there is no exact solution to this complex coupling system. So the approximated solution is needed in this model.

Secondly, due to the complexity and high-speed of chemical reaction mechanism in the explosive detonation. It is hard to deduce the equation which satisfies the reaction kinetics strictly,so phenomenological method is suggested. A great many of rate law has been proposed in the last decades, for example, Forest Fire model, JTF model [1,2,4,28]. The rate law used in this article is Wilkins rate law, which is given in the following form

where nbis a constant to be calibrated through the experiment,F1denotes the burning function associated with Chapman-Jouguet(CJ) specific volume, and F2denotes the burning function associated with time, which are defined through

where CJ specific volume vJ= γv0/（γ-1）, v0is the initial specific volume, and v is the specific volume, ΔL=rbΔR/DJ, ΔR is cell width;DJis the detonation CJ velocity,t is the current time.tbis the ignition time, which is calculated through Huygens principle. rbrefers to the parameter to be defined through simulation.It is clear that the parameters in the Wilkins rate depend on the cell size used for the simulation.

Thirdly, to establish a relation between the thermodynamic variables under the thermal and mechanical equilibrium, an appropriate EOS is needed. On the detonation driving device, it involves the explosive and non-reactive materials (it is usually in the form of metal).The EOS for the explosive and EOS for the nonreactive materials are both needed in the detonation modeling.But the EOS is also phenomenological in the detonation modeling,which has different forms.Much EOS has been proposed in the last decades. In this article, we consider EOS in the following forms:

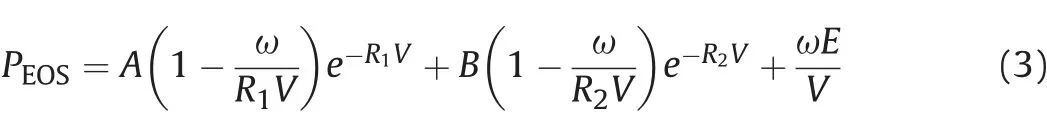
i. The Jones-Wilkins-Lee (JWL) EOS has been used extensively to describe the behavior of the detonation products in contact with metal casings, which has the form where E refers to the specific thermodynamic energy,A,B,R1,R2,ω are given by several references,V=ρ0/ρ refers to relative volume of the detonation products.In the practical application,we sometimes combine(3)with F to get the EOS of the condensed explosive P =PEOS× F.

ii. The perfect gas EOS can be applied to a large number of real detonation.For instance,γ=3 can be used to simulate product from the detonation of a high explosive

where γ denotes the ratio of specific heats.

iii. For a moderately realistic model, Mie-Grunneisen EOS has long been used by the detonation community for the simulations of metal materials,which are suitable for detonation,interact with metal. It has the following form

where ρ0denote the physical property parameters, C0is the bulk speed of the sound, Sα,γ0are the Grunneisen constants.

iv. The stiffened perfect gas EOS is also used when the material is Fe, where c denotes the local sound speed.

The parameters in the above forms of EOS do not have any physical meaning.It is calibrated through the comparison between simulation and experimental data. Uncertainty exists in these parameters. So UQ is also necessary in the detonation modeling.

By the way,the explosive Plastic-bonded explosive(PBX)is used in this article, which is an energetic material in which explosive powder is bounded through a small quantity of synthetic polymer.Specially,we choose two type of this explosive,PBX-9404 and PBX-9501, which is widely used in the atomic bomb. The experiments used in this paper are conducted on the China Academy of Engineering Physics.

2.3. Computational scheme of LAD2D

The computational method is based on the arbitrary unstructured polygonal grid. The Lagrangian compatible finite volume method and various viscosity such as classical Von Neumann-Richtmyer viscosity(the quadratic form viscosity), Landshoff viscosity(linear viscosity), shock wave viscosity, subzonal pressure method, artificial heat exchange in eliminating nonphysical deformation of Lagrangian mesh. The Von Neumann-Richtmyer viscosity q is used in the simulation, that is to say, P is replaced by p=P+q in the momentum conservation equation. The discretization of momentum equation in the Lagrangian hydrodynamics is achieved via a control volume differencing method along the median mesh. The reason why we choose it is that the finite volume method can deal with the flow problems in domains with a complicated geometry and its algorithm is simple. We limit ourselves to the vertex-centered control volumes in unstructured grids. A portion of two dimensional grid used for this discretization is shown in Fig. 2. Bases on above idea, we develop the detonation software LAD2D.

2.4. The structure of detonation software LAD2D

This software has fully intellectual property rights. It involves the physical modeling,numerical algorithm,and program practice.Fig.3 presents the structure of LAD2D;it is composed of calculation support layer, application support layer, assembly of application software and personality function layer of the application software.The simulation of detonation is implemented on the supercomputer in Beijing Institute of Applied Physics and Computational Mathematics, China.

3. Verification of detonation modeling

Verification of detonation modeling involves accuracy assessment of symmetry verification and conservation verification, as well as program verification.These verifications will be executed in this section.

3.1. Verification of symmetry preservation

The spherical shell model is one of the most fundamental theories of nuclear structure. Both spherically converging shock wave and bouncing flow exist in the spherical shell model,which is based on the implosion. However, this property can't be preserved, if there is a deficiency in the calculated algorithm of the software. It can be used to verify the spherical symmetry of the shock wave.

Fig. 4 was basic structure of spherical shell model. From Fig. 4,we can see that three zones exist in the spherical shell model,ideal gas is filled in the core of the ball, and wolfram (W)is filled in the two surrounded shells. The radius of the inner ball is 10cm, the thickness of the surrounded shell is 0.2 cm,and the thickness of the outer shell is 0.05 cm. The initial condition for the gas is ρ0=0.00129g/cm3,p0=10-4GPa,uR=0.0m/s,the initial density and pressure of W is: ρ0= 19.237g/cm3, p0= 10-4GPa, the initial velocity is=0.0m/s , uoutR= 2000m/s. To model the material properties of the explosive,the ideal gas EOS is used with γgas=1.4 for gas and γw=3.0 for wolfram.The free boundary condition is used in the outer boundary.

Fig. 5 presents the cell used for solving the problem and the pressure distribution at different times. We can see from the picture that the converging shock wave reaches its minimum radius at t =45μs,then into the expansion phase.The spherical symmetry is preserved during the whole process. That means the symmetry of algorithm and the correctness of the program is verified.

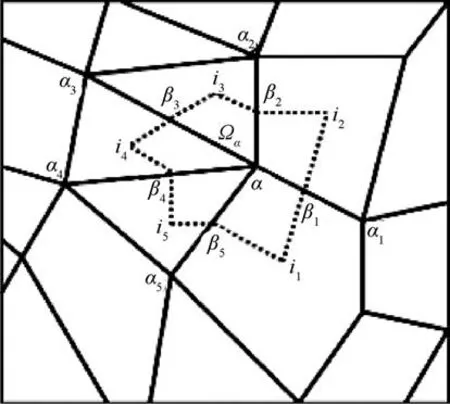
Fig. 2. Control volume Ωα of momentum equation.

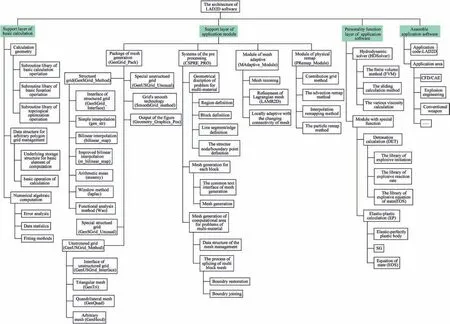
Fig. 3. Structure of the LAD2D software.

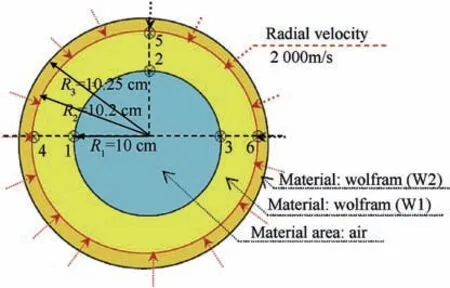
Fig. 4. Basic structure of spherical shell model.

3.2. Verification of conservation

The Noh or Newtonian wall shock problem is an important test for code that aims at simulating spherically collapsing systems such as Core-Collapse Supernovae(CCSNe)[1,2].It is often used to check the accuracy of the program and the conservation of the scheme.This problem can be studied in the planar,cylindrical and spherical coordinates. In this example, we consider the problem in one dimensional plane. The initial condition is ux0,0,ρx0,0,ex0,0,Px0,0T= （-1,1,0,0）T. The solid wall boundary condition is enforced as u（x0= 0,t） = 0, u（x0= 1,t） = - 1, the perfect gas EOS is used with γ =53,the exact solution of post-shock wave is u+=0,ρ+=4,e+=0.5,P+=the shock wave velocity is D=1/3. The CFL number is chosen to be 0.7. Fig. 6 statistically displays the evolution of kinetic energy (Ek), internal energy (Ei)and total energy(Et)versus time with Et =Ei+Ek =0.1.The total energy(Et)remain the same with the evolution of the time,so we can infer from the picture that this model satisfies the conservation of energy.So the conservation of the scheme and correctness of the program implementation are verified.

3.3. Theoretical verification of detonation simulation

There is no exact solution for detonation system in most cases.But the theoretical analysis is enormous in detonation field,such as CJ theory and existence of reflected shock wave in sliding detonation. We firstly compare the simulation result with CJ theory in planar detonation. Then, detonation structure verification is conducted through sliding detonation model initiated from one point.

3.3.1. One dimensional planar detonation

The computational domain for planar detonation model is chosen to be ［0,10］ (see Fig. 7). The initiation position is at left endpoint of the tube, the detonation wave will propagate to the right,the Wilkins function is used as the reaction rate law and the perfect gas EOS is used with γ =3.1.The PBX-9404 is used in this experiment, which is widely used in the nuclear weapons. In particular, the percentage of HMX is 95% in PBX-9404. Physical parameters used for PBX-9404 explosive are DCJ=8.88km/s,ρ0=1.842g/cm3.The corresponding Chapman-Jouguet states are:ρCJ=we can get PCJ=37.27GPa. Fig. 8 displays the evolution of detonation at time interval of 1μs.We can see from the picture that detonation pressure and detonation velocity reaches the CJ state at 2μs, and the threshold of detonation pressure and detonation velocity and the CJ state are in good qualitative agreement. That means the feasibility of the detonation calculation is verified.

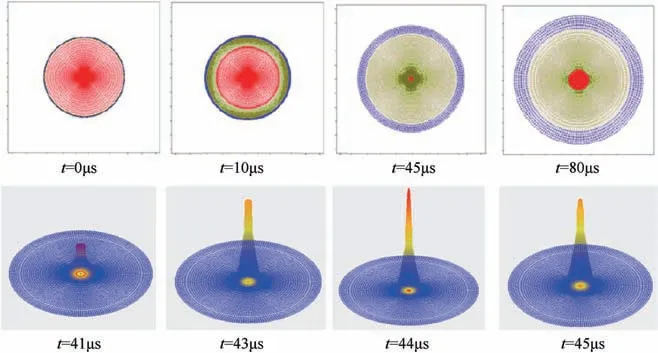
Fig. 5. The mesh and pressure distributions at different times.

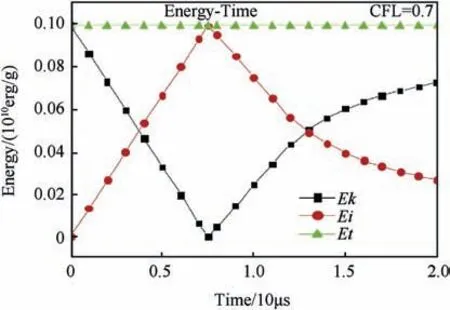
Fig.6. The conservation and exchange of the energy in one dimensional Noh problem.Ek denotes kinetic energy, Ei denotes internal energy and Et denotes total energy.

Moreover, due to the coagulation in homogeneity of the explosive materials in the practical manufacturing, the density of the explosive ρ varies in an interval involving 1.842g/cm3. ρ is assumed to satisfy a uniform distribution in ［1.842-0.1842,1.842+0.1842］g/cm3. Uncertainty quantification can be fulfilled by using the non-intrusive polynomial chaos, for detailed information about this method, please see Refs. [1,5]. The expectation and variance,even the confidence interval of P and ρ can be seen in Fig. 8 (a) and (c).

Fig. 7. The computational domain of planar detonation.

3.3.2. Sliding detonation model initiated from one point

The geometrical structure of this model can be seen in the left part of Fig.9.The radiuses of this zone are R1=3.0cm,R2=4.0cm,R3= 4.5cm, R4= 4.53cm, R5= 6.5cm, R6= 6.52cm, R7=6.8cm respectively.7 zones exist in this model,from the inner part to the outer part, it is filled with gas, wolfram (W), steel (Fe), gas, explosive,gas and W.The explosive is selected as widely used energetic material in the nuclear bomb-PBX-9501,in which the percentage of HMX is 95%. It is a challenge to simulate this phenomenon since multi-medium exists in this model and interact on each other.

The physical parameter for W is ρ0= 19.237g/cm3. The ideal gas EOS is used for W with γ = 3.0. The stiffened perfect gas EOS P =（γ-1）ρe+c20（ρ-ρ0） is used for Fe, with γ = 4.075, ρ0=7.85g/cm3, c0= 4.2km/s. Though computation, we get the calculated pressure distribution at different times in Fig. 10. The reflected shock wave exists clearly in Fig.10,which coincides with the detonation structure and involution process inferred from theoretical analysis. So the correctness of multi-medium detonation is verified.

4. Validation of the detonation modeling

Model validation is conducted by comparing the experimental measurements with the simulation result. We will execute model accuracy assessment quantitatively through cylindrical test. However, the data in some detonation experiments is usually given in the form of photo, so we cannot validate the model the quantitatively. The validation is fulfilled by successively simulate some special phenomenon of the detonation in this situation.

4.1. Validation hierarchy tiers

Detonation wave is a shock wave that proceeds and driven by a zone of chemical reaction. It is difficult to design an experiment suited for all phenomenon and validate the full process of the detonation.We split the whole system into several simple units for the convenience of validation under the hierarchy tiers methodology of V&V. For detailed information detonation decomposition,please see Fig. 11. We will conduct validation on the two subsystems of the detonation, one is cylindrical experiment, and the other is diffraction phenomenon.

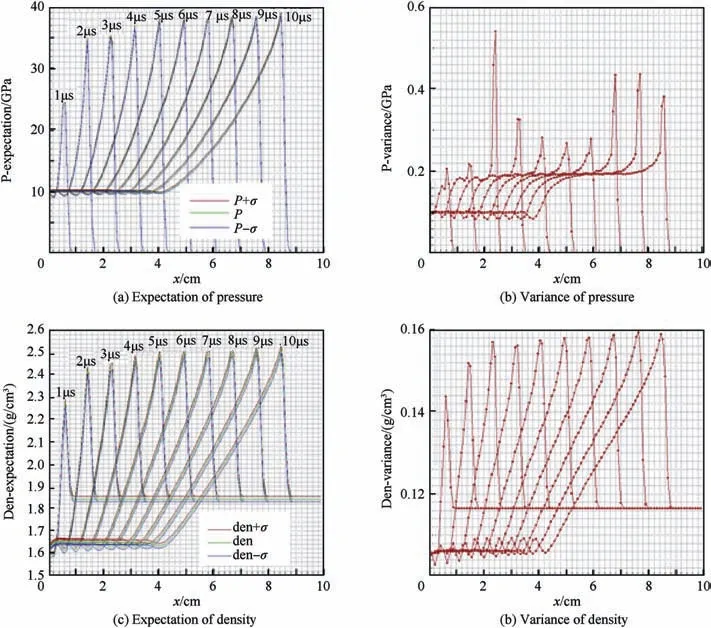
Fig. 8. The expectation and variance of pressure and density profiles at different times, where σ denotes the standard variation of corresponding variable.

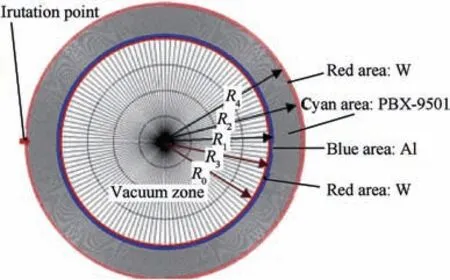
Fig. 9. The computational domain of one point initiation.

4.2. Model accuracy and uncertainty quantification of cylindrical test

4.2.1. Model accuracy of cylindrical test

The cylindrical test is perhaps the most common experiment designed for explosive model validation[19].This test is developed at the Lawrence Livermore Laboratory (LLNL), with the aim of characterizing the expansion of the detonation products. This is commonly used to calibrate the parameters in the detonation products EOS, and validate the accuracy of the model. Fig.12 depicts the experiment of the experimental configuration and the computational domain. The center point initiation position is at O.

The Mie-Gruneisen equation is used as the EOS for red copper.

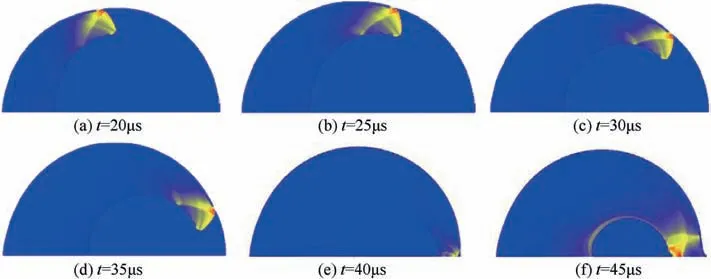
Fig.10. Panels (a)-(f) display the distributions of pressure P at different times.

The physical parameters for red copper are ρ0=8.39g/cm3,c0=3.94km/s , Γ=2.77358 , λ=1.46 . The physical parameters for explosive JOB9003 are ρ0= 1.849g/cm3, K=2.77358, DJ=8.712km/s.JWL EOS is used for this explosive with parameters are:A = 7.637, B = 0.21445, R1= 4.5, R2= 1.5, ω = 0.3283. We can also get the CJ state by using these parameters in the standard detonation theory [1], we obtain that: PJ= 37.19GPa,uJ=2.18346km/s ,ρJ=2.46739465g/cm3, eJ= 7.163216J/mm3,Q =8.8372KJ/g . The explosion initiation time is computed through the Huygens principle. LAD2D is used to simulate the cylindrical test. Fig.13 describes the comparison between computational result and experimental data in velocity and tube expansion.The experimental data is from China Academy of Engineering Physics, which serves as a benchmark test. Through computation,the relative error of velocity between the computational result and experiment data is 4.06%, and the relative error of wall radius is 1.35%. That means computational result match the experiment well. Meanwhile, the JWL parameters in the explosive detonation are calibrated through the software LAD2D.

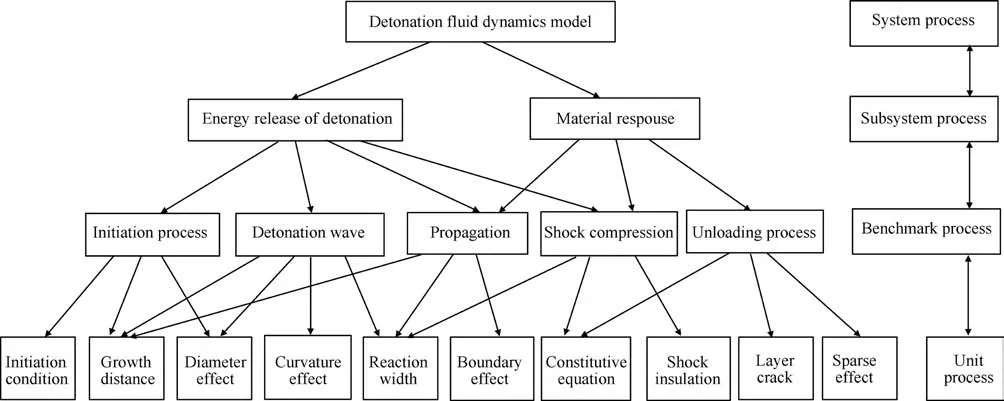
Fig.11. Validation hierarchy tiers of the detonation CFD model.

4.2.2. Uncertainty quantification through entropy theory

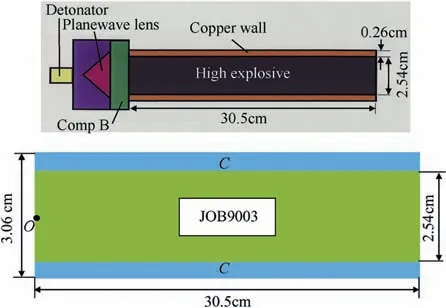
Fig.12. A schematic diagram of the cylinder experiment and calculation model.

Uncertainty also exists in the cylindrical test due to the error of technique of measurement. However, only a few samples can be obtained because of high experimental cost.It is difficult to confirm the type of probability distribution for these data, so it hard to describe it through the classical probability approach. This type of uncertainty is usually tackled through the non-probabilistic method since lack of knowledge or data. The entropy theory is originally proposed by Shannon, which is a good tool to deal with the information uncertainty. We use the general entropy theory proposed by X. Wang and L. Wang [29] to deal with uncertainty quantification in detonation system.

Cylindrical tests are conducted, so 8 samples at 25μs are obtained and given in Table 1.For application,we arrange the set from small to big, and these data are denoted as x（k）,k = 1,2,...,8.

Took one of the bags of gold under his arm: Some versions of the story, such as Tabart s version, make Jack a righteous trickster character by justifying55 his thievery from the giant

Following the procedure in X.Wang[29],the estimation of rank rkis expressed as rk=k =1,2...,n,where n =8.So,the set ofu） is The estimation of information entropy of u in the discretization forms is given as

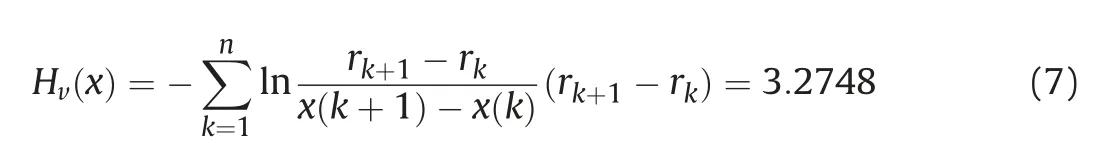
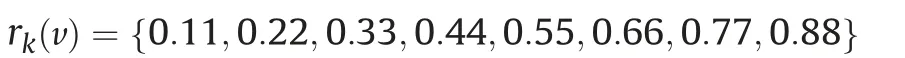
Correspondingly, the expanded uncertainty Uuebecomes

Therefore,the estimated interval with regard to the true value of wall velocity u at 25μs based on Table 1 is given as followsis adjustment factor and is chosen as kt=1.5[29].

wherex =

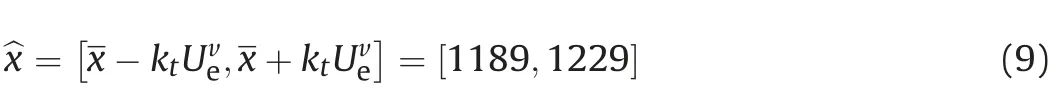
4.3. Validation of the detonation structure by using the detonation diffraction

Diffraction of a detonation wave behind a backward-facing step is one of the fascinating topics in shock wave dynamics and is studied extensively by many researchers. This problem deals with detonation wave propagating through the channel with sudden expending section(see Fig.14).80 years ago,many scholars such as Weibull believed that the detonation wave propagate in the explosive with constant speed in all directions[30].But it was first observed by Metchell and Paterson in 1947 that the conclusion is wrong [31]. C. Mader and C. Forest first successfully simulate this phenomenon for triaminotrinitrobenzene (TATB) based explosive X-0219 turns over a corner with HOM EOS and Forest Fire rate law in 1976[32].Then many scholars have devoted to this field both in the experiment and numerical simulation [33,34]. We use our developed LAD2D software simulate the detonation diffraction phenomenon in the TNT explosive with JWL EOS and Wilkins rate law in(2). Numerical simulation is utilized in order to validate the predicative capabilities of the new automatic local remeshing method for problems with large deformations based on Lagrangian methods.

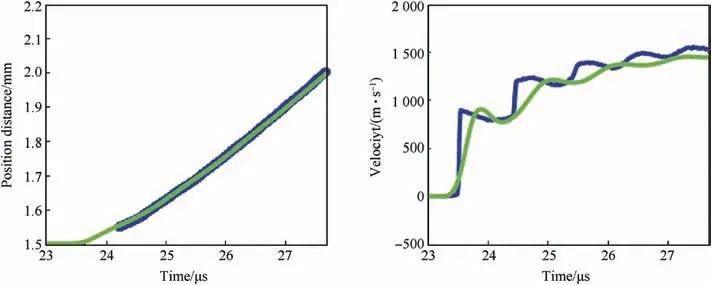
Fig.13. Curves of wall expansion radius and velocity in the cylinder test.(The blue dashed line stands for the experiment data, and the green solid line stands for the calculation result.).

Table 1The experimental data for wall velocity in different cylindrical test at 25μs.

The computational model and experimental setup for diffraction of detonation can be seen in Fig.14. We can see from Fig.14 that Ωconsists of two regions, which is filled with TNT. The left is a small section channel Ω1=［0,3.0］×［0,0.5］,the right region is a larger section channel Ω2=［3.0,6.0］×［0,3.0］ . Ω1is the driver section, and the upper boundary is a solid-wall condition; the bottom satisfies an antisymmetric condition. JWL EOS is used for detonation products with parameters A=852.4 , B=18.02 ,R1=4.6 , R2=1.3 , ω = 0.38. The perfect gas EOS is used for explosive with γ=3.11 , ρ0= 1.6g/cm3, DCJ= 6.9km/s. The Wilkins rate law is used in this article.

Firstly, the explosive is ignited in the left of Ω, a steady CJ detonation wave propagates through the narrow segment, and begins its travel through the narrow channel Ω1as a steady, undisturbed wave. It first senses a change in geometry upon arriving at the corner. As the detonation wave rounds the corner, the diffraction and re-initiation of detonations behind a backward facing step generates a spherical detonation wave. The detonation wave is weakened to deflagration partly in following the detonation diffraction.The slip line is occurred,and the Mach reflection of detonation wave has formed when the detonation wave interacts with the wall.As time elapses,the reflected wave interacts with the back-face of the step where a vortex exists near the line of symmetry (lower boundary of the computational domain). The wave becomes the planar wave, the Mach reflection takes place and the reflected wave reflects off the upper wall again. Detonation wave propagates through the corner of also generates a stronger corner vortex. For detailed information, please see Fig.15.

However, because the reaction zone scale is smaller than the scale of the experiments of interest, the data in the detonation diffraction is usually in the form of photo as that in the bottom of Fig. 15, which obtained from the laboratory of China Academy of Engineering Physics. It is difficult to validate this example quantitatively since the measurement result of detonation is given in the form of photo. So we can't give the comparison between the computational result and experiment result. But the validation of detonation is fulfilled by the success of obtaining the corner vertex effects in this test.

Fig.14. Geometrical models of detonation diffraction and experimental setup. (Left: experimental setup; Right: geometrical structure.)

Fig.15. The comparison between the numerical results and the experimental data at different times(Top:grid used for solving the detonation diffraction;Center:density contour from calculated result; Bottom: data from the schlieren photography.).

5. Conclusion and discussion

This article systematically presents the basic principle of V&V&UQ based on the detonation software in the form of coupled nonlinear partial differential equation. We also give the basic activity of the code verification, algorithm verification, calculation verification and validation. Meanwhile various methods of experiment measurement, validation model hierarchy, experiment validation and uncertainty quantification of self-developed multiphysics detonation are also shown in this paper,and get a satisfied result. This can provide a useful guidance on the correctness verification and adaptability validation of the CAE software. However,V& V of detonation is a systematic work, we can't discuss all the methods in one paper, so we select some classical and efficient methods which are suitable for detonation system in this paper.Other methods will be explored in the future work.

The V&V technology has become the standard procedure in developing the high fidelity simulation software, the implementation of V&V has taken place on the commercial software. In some industrial field, 70% of the physical experiment has been replaced by the simulation, even in some cases, the simulation provides all of the important breakthroughs in research and technology. So self-developed software about V&V&UQ will take an important role in the future. But there is still some theory and methodology needs to be answered in the V&V field as follows.

(1) The research of V&V in complex system has taken place for several decades, but it is still in the infantile state, little scholars pay attention to this field.Recently,V&V is earnestly needed in the M&S of science and technology.They want to design high fidelity software in their special field. However,they do not know how to use the V&V in the software. The standard, guideline as well as procedure of the V&V is earnestly needed in the detonation fields.

(2) Software test is indispensable to V&V activity, and high quality benchmark test is needed in the software test. The construction of test library of detonation software which can be used to assess the model is the further research direction of V&V implementation.

(3) It is true that only a few cases are discussed in this paper.The reason is that the V&V of detonation is a systematic work and it needs to be studied step by step. There is no experiment suited for all phenomenon of the detonation. So we select some classical and efficient cases which are suitable for V&V of detonation modeling. Especially spherical shell model,Noh wall shock problem, planar detonation are used for verification. Detonation diffraction problem is used for validation.Cylindrical test is used for uncertainty quantification.By the way,we can't use all the methods listed in one paper.We just choose some efficient methods in this article.Other cases and methods will be explored in the future work.

(4) More and more engineers take care of automatic testing in the software testing field. Regression test and performance test are prevalent in the software testing.But little automatic testing can be found in the engineering technology. Along with the enlarging scale of the program, we must pay great attention to this issue.Otherwise software maintenance will become a catastrophe in the future. So automatic testing of utility software in the complex engineering will become an important research direction in the future.

(5) The MMS verification technology in the higher dimensional detonation fluid mechanics is still an open problem.The MES and MMS are the two rigorous methods to verify the code.The disadvantage associated with MES is that there are only a limited number of exact solutions to the complex nonlinear equations. The MMS is a more general and powerful approach to code verification.The MMS for code verification in multi-physics coupling detonation in the Lagrangian coordinates will be studied in the future.

(6) The multi-physics process is usually very complex in the engineering field involved with differential equations. we can't accomplish the whole task of V&V at one stroke due to its complexity. Validation model hierarchy method is regraded as a potential tool for V&V of detonation.

(7) Traditional probability is a useful formalism for UQ.But it is sometimes difficult to judge whether some parameters satisfy specified distributions due to small sample size. In practice,independence or stationary assumption is also hard to justify. It will be a challenge to study the quantification and propagation of the uncertainty in this extreme situation.We will regard these uncertainties as epistemic uncertainties. Entropy information and fuzzy mathematics as well as P-box are some potential methods to deal with uncertainty quantification and propagation for epistemic uncertainty in the experiment.The comparison between these methods also will be conducted in the future work.

Acknowledgement

This work was supported by Science Challenge Project [No.TZ2018001], Shandong Provincial Natural Science Foundation [No.ZR2017BA014], National Natural Science Foundation of China [No.91630312], and the Development Program for Defense Ministry of China [No. C1520110002]. The first author also thanks Shandong University of Science and Technology for providing funds for his visiting career in University of Southern California,Los Angeles,CA.