桩土相互作用对公路连续刚构桥地震响应的影响研究

■魏 嬿

(福建省交通规划设计院有限公司，福州 350004)

近年来，随着高速公路的大规模建设，连续刚构桥由于跨越能力强、伸缩缝少、节省大吨位支座等特点而得到了广泛应用。在连续刚构桥的设计过程中，如何确保其抗震性能是该类桥梁面临的关键技术问题。由于东南沿海软土高度发育，连续刚构桥的基础大多采用群桩基础，桩土耦合效应突出，这给该类桥梁的抗震计算进一步增加了难度。探明桩土相互作用对桥梁地震响应的影响，对于简化桥梁抗震计算、快速评估桥梁的抗震性能以及优化桥梁的抗震设计都具有重要意义。

关于桥梁的桩土相互作用问题，一些学者进行了深入研究[1-5]。例如，江博君等研究了桩土相互作用对高速铁路桥梁地震响应的影响[1]；孙利民等研究了桥梁抗震计算中桩土相互作用计算模型的选取和参数的确定方法，提出了一种改进的Penzien模型[2]；李帅等研究了桩土相互作用对曲线梁桥抗震性能的影响，得出对于受力较大的桥梁需考虑桩土相互作用[3]；黄平明等研究了桩土相互作用对钢混组合连续梁桥抗震性能的影响[4]；Duncan等通过建立完整的有限元分析模型，研究了桩土相互作用对全桥桩基受力性能的影响[5]。除此之外，还有部分学者针对桩土相互作用的其它相关问题进行了研究[6-10]。然而，上述研究成果很少涉及桩土相互作用对公路连续刚构桥地震响应的影响，这对于该类桥梁的抗震性能优化十分不利。

1 基本理论和计算模型

1.1 工程概况

以福建永定至南靖高速公路某(60+110+60)m连续刚构桥方案为工程背景，桥址区地震动峰值加速度为0.15g，地震动反应谱特征周期为0.4s，抗震设防烈度为7度。主梁采用变截面单箱单室混凝土箱梁，底板宽6.75m，顶板宽12.75m，边支座处梁高3.0m，刚构墩处梁高6.5m。下部结构采用箱型墩配桩基础，从左往右依次编号为1#～4#，桥墩高度分别为48.6m、57.6m、68.7m和45.5m，1#和4#箱墩下配置4根直径为2m的群桩基础、桩长分别为19m和20m，2#和3#箱墩下配置4根直径为2.8m的群桩基础、桩长分别为16m和14m。1#和4#箱墩截面为6m×3m，2#和3#箱墩截面为6m×4m，结构总体布置见图1所示。

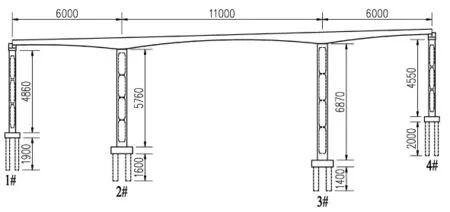
图1 结构总体布置图(单位：cm)

1.2 有限元模型

采用MidasCivil2019建立该连续刚构桥的空间有限元模型，包括考虑桩土相互作用的群桩基础模型和不考虑桩土相互作用的等效承台模型。其中，主梁、桥墩、承台、桩基均采用三维梁单元模拟，每个单元包含两个节点，每个节点包含3个平移和3个转动自由度。1#和4#交界墩墩顶与主梁梁底通过主从自由度连接，2#和3#刚构墩墩顶与主梁形心通过刚臂连接，桥梁的二期恒载取100kN/m，沿主梁均匀分布。在群桩基础模型中，桩土之间的相互作用采用m法通过土弹簧模拟，土弹簧的刚度依据土层的性质、厚度等参数参考规范《公路桥梁地基与基础设计规范》(JTGD63-2007)附录P计算[11]。等效承台模型在承台底通过6个弹簧刚度等效群桩的作用，承台底的等效刚度参考文献[12]计算。建立的全桥空间有限元模型见图2，等效承台模型的等效承台底刚度如表1所示。

图2 全桥空间有限元模型

表1 等效承台底刚度

为了验证所建立的有限元模型的正确性，采用子空间迭代法分别计算了两种模型的自振特性见表2，第1阶振型对比见图3。

表2 桥梁频率及振型(单位：Hz)

图3 第1阶振型图对比

由表2和图3可见，群桩基础模型和等效承台模型主要振型的频率出现了差异，且相同振型时群桩基础模型的自振频率大于等效承台模型。由此说明，不考虑桩土相互作用可能低估该公路连续刚构桥的整体刚度。

2 地震波输入与选取

针对建立的群桩基础模型和等效承台模型，本文不考虑地震动空间变异性的影响，采用一致激励模式输入地震波，并通过MidasCivil2019中的地面加速度选项实现，其基本动力学方程可表达为公式(1)：

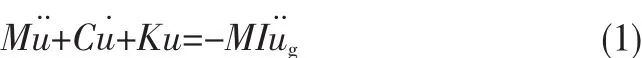
式中，M、C、K分别表示结构的质量矩阵、阻尼矩阵和刚度矩阵，其中M采用集中质量矩阵、C通过瑞利阻尼模型模拟；I表示单位矩阵；u¨、u˙、u 分别表示节点的加速度、速度和位移列向量；u¨g表示输入的地震波加速度时程。

根据桥址区的反应谱特征周期，按照《建筑抗震设计规范》(GB50011-2010)2016年版中的选波原则，在太平洋地震工程研究中心(PEERGroundMotionDatabase)中选取了3条实测地震记录作为输入，地震波编号分别为RSN289、RSN581和RSN6，其加速度时程如图4所示。

图4 输入地震波

将上述地震波进行规格化处理，其峰值加速度PGA调整至桥址处的设计地震动峰值0.15g，则RSN289、RSN581、RSN6 的调整系数分别为 1.1085、0.9171 和0.5256。将规格化后的地震波按公式(1)输入建立的群桩基础模型和等效承台模型，即可进行动力响应计算。计算时，两种模型的阻尼比均取0.05、时域积分步长取0.01s。

3 数值计算结果分析

3.1 对纵向地震响应的影响

首先，分别将规格化后的RSN289、RSN581和RSN6地震波沿纵桥向输入，探讨桩土相互作用对桥梁纵向地震响应的影响。图5～图7分别给出了两种模型3#墩墩底的弯矩时程、剪力时程和墩顶的位移时程。

图5 3#墩墩底纵向弯矩时程对比

图6 3#墩墩底纵向剪力时程对比

图7 3#墩墩顶纵向位移时程对比

由图5～图7可得，当地震波沿纵桥向输入时，群桩基础模型和等效承台模型3#墩墩底的弯矩时程、剪力时程和墩顶的位移时程波形相似，但幅值不同，桩土相互作用对该桥的纵向地震响应有影响。进一步考察桩土相互作用对桥梁纵向地震响应幅值的影响，取3条地震波动力响应幅值的平均值进行对比，2#和3#墩墩底的弯矩幅值、剪力幅值以及墩顶的位移幅值对比结果如表3所示。

由表3可得，当地震波沿纵桥向输入时，不考虑桩土相互作用计算的弯矩、剪力均偏小，其中2#墩墩底的弯矩偏小35.2%、剪力偏小26.9%。同时，不考虑桩土相互作用时，2#墩和3#墩墩顶的位移幅值均偏大，最大达20.0%。由此说明，桩土相互作用对该公路连续刚构桥纵向地震动响应的影响巨大，在进行抗震计算时不考虑桩土相互作用会低估桥梁的纵向地震响应。

3.2 对横向地震响应的影响

将地震波沿横桥向输入，进一步考察桩土相互作用对该公路连续刚构桥横向地震响应的影响。图8～图10分别给出了RSN289地震波作用下3#墩横桥向的动力时程对比。

图8 3#墩墩底横向弯矩时程对比

图9 3#墩墩底横向剪力时程对比

图10 3#墩墩顶横向位移时程对比

由图8～图10可得，当地震波沿横向输入时，群桩基础模型和等效承台模型的墩底弯矩时程、剪力时程和墩顶的位移时程波形相似，但出现了相位差，且幅值大小也不相同。其中，群桩基础模型计算的横向弯矩、横向剪力大于等效承台模型，且群桩基础模型计算的横向位移小于等效承台模型。由此说明，桩土相互作用对该连续刚构桥的横向地震响应有影响。进一步考察桩土相互作用对该桥横向动力响应幅值的定量影响规律，取3条地震波计算结果的平均值进行对比，2#和3#墩墩底的横向弯矩幅值、横向剪力幅值以及墩顶的横向位移幅值对比见表4所示。

由表4可得，当地震波沿横桥向输入时，不考虑桩土相互作用计算的横向弯矩、横向剪力均偏小，而横向位移偏大。其中，2#墩墩底的横向弯矩偏小27.4%、横向剪力偏小29.2%、墩顶的横向位移偏大64.9%。由此可见，桩土相互作用对该连续刚构桥横向地震响应的影响剧烈，不考虑桩土相互作用会使得横桥向内力偏小、位移偏大，可能使抗震验算出现错误。

表4 横向地震响应幅值对比

3.3 对地震响应频率的影响

由于篇幅有限，仅将RSN289地震波计算的纵向地震响应和横向地震响应时程进行FFT变换，考察桩土相互作用对该桥动力响应频率成分的影响。图11和图12分别给出了群桩基础模型和等效承台模型计算的3#墩墩底弯矩和墩顶位移的傅里叶幅值谱对比曲线。

图11 3#墩墩底弯矩的傅里叶幅值谱对比

图12 3#墩墩顶位移的傅里叶幅值谱对比

由图11和图12可得，群桩基础模型和等效承台模型计算的3#墩的纵、横向地震响应傅里叶幅值谱有差异。其中，等效承台模型的纵、横向弯矩和位移傅里叶幅值谱的卓越周期比群桩基础模型略低，但差异不大。由此可见，桩土相互作用对该桥地震响应的频率成分有影响，但影响有限。

4 结论

本文基于桥梁的桩土相互作用理论，以福建永定至南靖高速公路某(60+110+60)m连续刚构桥方案为工程背景，分别探讨了桩土相互作用对结构纵向地震响应、横向地震响应以及地震响应频率成分的影响，得到了以下几点结论：

(1)群桩基础模型比其相应的等效承台模型刚度大，自振频率略高，不考虑桩土相互作用会低估结构的整体刚度。

(2)桩土相互作用对该公路连续刚构桥纵向和横向地震响应的影响都很剧烈，不考虑桩土相互作用会使计算的弯矩、剪力偏小，位移偏大，会使得抗震验算偏于不安全。

(3)对于本文的计算条件，不考虑桩土相互作用时，2#墩墩底的纵向弯矩偏小35.2%、纵向剪力偏小26.9%，墩顶纵向位移偏大20.0%。而横向弯矩偏小27.4%、横向剪力偏小29.2%，墩顶横向位移偏大64.9%。

(4)不考虑桩土相互作用会使纵、横向地震响应的傅里叶幅值谱的卓越周期略低，但总体而言，其对地震响应频率成分的影响有限。

本文只针对一致激励下公路连续刚构桥的桩土相互作用进行了研究，得出的结论可为该类桥梁的抗震计算提供参考，然而针对该种桥型，非一致地震激励时桩土相互作用的影响还需进一步探讨和研究。