长绒棉精梳牵伸工艺优化

豆孝坤，任家智，张一风,2，章 伟,2

(1.中原工学院 纺织学院,河南 郑州 450007;2.中原工学院 纺织服装产业河南省协同创新中心,河南 郑州 450007)

0 引 言

牵伸是纺纱过程中极其重要的一道工序，主要是将须条抽长拉细，使须条逐步达到预定的线密度[1]；同时，被前罗拉握持的快速纤维在从周围纤维丛中抽出时，在摩擦力作用下，纤维弯钩将逐渐消除，须条内部纤维伸直，平行度提高，成纱质量指标明显改善[2-3]。牵伸工艺参数的选择对须条的牵伸质量有直接影响，牵伸工艺配合不当，将造成纤维损伤、牵伸不开、须条条干均匀度恶化等问题，经过后道工序加工，易造成成纱断裂强度下降，毛羽数量增多，成纱条干均匀度下降，成纱千米粗、细节，棉结剧增[4-7]。在牵伸工艺上，张弘强[8]、蒿培建[9]研究了牵伸前、后条子中纤维排列的变化；卢远航、陈革等研究了牵伸波对成纱质量的影响[10-11]；朱耀麟等[12]通过建立自调匀整系统的数学模型,对喂入棉条定量检测点和输出棉条定量检测点进行相关分析，最后确定系统的实时长度延迟计算；宋栓军[13]、冯清国[14]研究了细纱牵伸区牵伸力的测量方法和其对细纱质量的影响；文献[15-16]分析了纤维在牵伸过程中的蠕变特性和纤维拉伸倍数与纤维长度、工艺参数间的关系等。张婉婉等[17]提出了一种基于改进平滑滤波和均匀性度量算法的纱线条干均匀度检测算法。但是在精梳工序牵伸工艺参数的优化及其对成纱质量的影响方面缺少相应研究与分析。本文 采用二次通用旋转组合设计对精梳牵伸工艺进行优化设计，在精梳及纺纱工艺参数相同的条件下利用长绒棉进行纺纱试验，对成纱质量指标进行测试、建立质量指标与工艺参数间的回归方程，并对回归方程和回归方程系数的显著性进行检验，得出有效回归方程，最后目标规划法得出最优工艺。

1 实 验

1.1 原料

采用100%新疆长绒棉，精梳小卷定量为66 g/m。利用USTER AFIS PRO 2测试得到精梳棉卷的总棉结数80 粒/g，纤维棉结数75 粒/g，总杂质数27 粒/g，上四分位长度38.9 mm，16 mm以下质量和根数短绒率6.9%和21.2%。

1.2 纺纱工艺流程及工艺参数

纺纱线密度为14.58 tex，纺纱工艺流程如下：JSFA2186型精梳机→JWF1310并条机→BHFA498粗纱机→FA507细纱机。各工序工艺参数设置如表1～4所示。

表 1 JSFA2186型精梳机主要工艺参数

表 2 JWF1310并条机主要工艺参数

表 3 BHFA498粗纱机主要工艺参数

表 4 FA507细纱机主要工艺参数

1.3 测试仪器及指标

测试条件：测试温度20℃，相对湿度60%。

利用USTER AFIS PRO 2测试精梳条棉结(个/g)、杂质含量(个/g)，纤维长度分布以及16 mm以下短纤维含量(%)，测试次数10次/试样；利用电子天平测量落棉率(%)，测试次数5次/试样。

利用USTER条干仪测试精梳条条干均匀度，测试速度50 m/min，测试时间2 min，成纱条干CV值、成纱棉(+200%)、千米粗节(+50%)和千米细节(-50%)含量，测试次数5次/试样，测试速度400 m/min，测试时间2.5 min。

利用YG063T全自动单纱强力仪测试成纱断裂强度(cN/tex)，测试次数10次/试样；利用YG172纱线毛羽测试仪测试成纱3 mm毛羽，测试次数10次/试样。

2 工艺参数优化实验

2.1 实验设计

通过前期的试验，设主牵伸罗拉中心距x1，后区牵伸罗拉中心距x2，后区牵伸倍数x33个参数为试验因子，采用三元二次通用旋转组合设计试验[18]。因子编码见表5。

表 5 因子水平编码表

根据实验设计,在纺纱工艺流程及纺纱各工序参数相同条件下进行20次实验,具体实验方案和测试结果见表6。

表 6 精梳及成纱质量指标测试结果

2.2 回归方程的建立

建立牵伸工艺参数与成纱质量指标的回归方程模型如下：

(1)

根据表6，采用最小二乘法计算成纱各质量指标回归方程的系数，如表7所示。

在进行统计检验前，成纱质量指标与牵伸工艺参数之间的线性关系仅是一种假设，还需对回归方程进行显著性检验，其显著性检验结果如表8所示。

在回归方程显著的前提下，对初始回归方程的回归系数进行检验，剔除对回归方程的结果影响较小的回归系数，在0.3的显著水平下，剔除不显著的回归系数后回归方程如表9所示。

表 7 纱线各质量指标的回归系数

表 8 回归方程显著性检验结果

表 9 各指标的有效回归方程

2.3 因子交互作用及等高图分析

因素间的交互作用分析是将其中一个因素在零水平下固定, 然后将剩余的2个因素进行交互作用分析。 利用 Design-Expert 数据处理软件绘制水平因子和质量指标之间的关系。 因本次实验成纱质量指标较多, 在此仅以成纱条干为例进行分析, 成纱条干与牵伸参数之间交互作用的三维等高图如图1所示。

由图1(a)可知,主牵伸罗拉中心距较小时，随着后区牵伸罗拉中心距增大，成纱条干CV值增大；主牵伸罗拉中心距较大时，随着后区牵伸罗拉中心距增大，成纱条干CV值减小；在主、后区牵伸罗拉中心距都较小时成纱条干CV值达到最小。这是因为牵伸罗拉中心距较小，前后罗拉对须条的控制作用都较大，须条中浮游区较短，在前后罗拉形成的摩擦力界作用下纤维更易有序输出，此时的精梳条及成纱条干均有较大改善。由图1(b)可知,主牵伸罗拉中心距较小时，随着后区牵伸倍数增大，成纱条干CV值减小；主牵伸罗拉中心距较大时，随着后区牵伸倍数增大，成纱条干CV值急剧增大；在两者均取中间值时，成纱CV值较小；为了保证成纱条干良好，在主牵伸罗拉中心距较小时，后区牵伸倍数偏大掌握较好。由图1(c)可知,后区牵伸罗拉中心距和后区牵伸倍数的交互作用对成纱条干的影响较小，两者均偏小掌握能降低成纱条干。

(a) 成纱条干与主牵伸罗拉中心距、后区牵伸罗拉中心距的关系

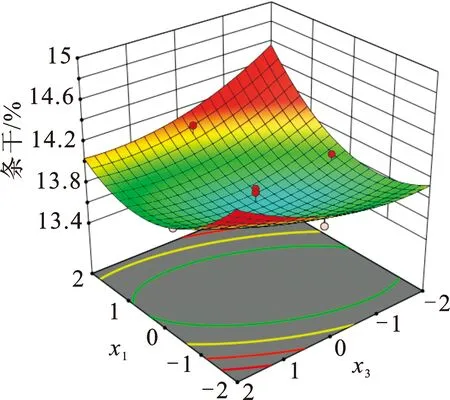
(b) 成纱条干与主牵伸罗拉中心距、后区牵伸倍数的关系

(c) 成纱条干与后区牵伸罗拉中心距、后区牵伸倍数的关系图 1 成纱条干与牵伸参数之间的三维等高图

2.4 工艺参数优化的数学模型及求解

利用最优化试验设计求得的各试验因子与考察指标之间的高精度有效回归方程,可用目标规划法建立优化数学模型。选取f1(x)=y条干,f2(x)=y断裂强度,f3(x)=y棉结为目标函数,细节、粗节和毛羽的约束条件为y细节≤12个/km,y粗节≤51.66个/km,y毛羽≤3.7根/m。这是约束多目标求极值的问题。目标函数可构造如下:

f(x)=(f1(x)/13.53-1)2+

(f2(x)/24.5-1)2+

(f3(x)/82.5-1)2

(2)

目标函数f(x)越小,得出的方案越优。运用Design-Expert数据处理系统对回归方程进行分析,计算可得x1=-0.146 37,x2=-0.556 2,x3=-1.208 84。解码得,主牵伸罗拉中心距为44.74 mm,后区牵伸罗拉中心距为52.01 mm,后区牵伸倍数为1.35倍。

2.5 试验验证

为了验证上述优化数学模型所求的最优解，以主牵伸罗拉中心距为44.74 mm,后区牵伸罗拉中心距为52.01 mm,后区牵伸倍数为1.35倍，其他工艺参数不变，进行纺纱试验。纱线指标测试结果如表10所示。

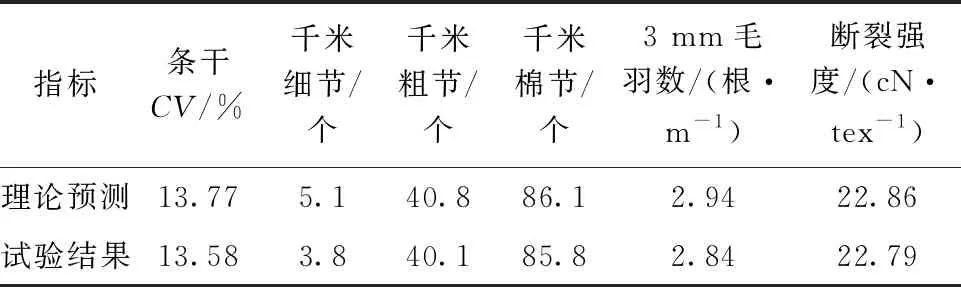
表 10 优化结果及试验结果对比

由表10可知,试验结果数值与优化结果十分接近，说明拟合较好，优化结果是可靠的，优化的数学模型能预测成纱质量。

3 结 语

利用二次通用旋转组合设计优化精梳机车尾牵伸工艺参数。在现有原料及试验条件下精梳牵伸最优工艺为：主牵伸罗拉中心距44.74 mm,后区牵伸罗拉中心距52.01 mm,后区牵伸倍数1.35。纱线质量指标的数学模型与实际试验拟合较好，可以用做纱线质量指标的预报。