DB模式年金计划现金流量测算模型的构建分析
中国人寿养老保险股份有限公司安徽省分公司 张曦
1 引言
基本养老保险、企业/职业年金计划、个人商业养老保险构成了我国养老保险制度的三大支柱。从积累与给付的角度,年金计划可分为收入确定型的DB(defined benefit)模式和缴费确定型的DC(de f i ned contribution)模式。近年由于企业年金的快速发展,DC模式日渐成为主流。DB模式和DC模式各有利弊:DC模式下,参与人从加入年金计划到退休,由企业和参与人按照一定的比例计提缴费金额,缴费水平相对固定,而年金资产的投资收益受资本市场的影响较大,以及缴费与待遇支付的定价日不同都会导致实际积累额和待遇支付额的不确定,风险由参与人个人承担;DB模式下,年金计划管理人做出参与人的养老金按事先约定水平发放的承诺,由年金计划承担投资的市场风险和参与人的长寿风险,退休待遇稳定可预期。作为第一支柱的基本养老保险采用的就是由政府管理的强制DB模式;作为第二支柱的年金计划中,由财政全额供款的职业年金计划每年按照国家统一公布的记账利率计算利息,参与人退休时由财政拨付计实,因此也将偏好DB模式。
1.1 理论意义
现金流量分析是一种成熟的财务分析方法,广泛应用于企业经营管理、投融资决策、业绩评价与上市公司信息披露等领域。现金流量表是企业财务报告必须编制的报表,成为会计活动的重要组成部分。付海龙(2009)借用生命科学理论,重述了现金流量表的分析框架;焦健(2016)研究了现金流量视角下的分红与可持续增长的关系;王斌斌(2017)更加关注与现金流量的质量和预警机制。
在年金计划研究方面,王芬(2005)对DB与DC模式进行了比较研究;郑秉文、黄念试证了美国DB模式年金计划的偿付能力存在财务风险和不可持续性;孙华平(2008)提出了DB模式和DC模式的精算模型原理;段明媛、吕诗慧(2017)在延迟退休的背景下分析了企业年金制度的精算模型。通过检索发现,目前尚无现金流量视角下关于年金计划DB模式的研究,本文可尝试填补此领域的研究空白。
1.2 现实意义
2018年人社部和财政部联合发文的《企业年金管理办法》(第36号令)正式执行,标志着企业年金进入到了一个新的发展阶段。截至2019年2月末,已有中央和8个省份的职业年金完成了招标启动工作。相较于DC模式,DB模式的资金管理复杂,对统筹规划能力和测算的准确性要求高,需要保持现金流入流出的动态平衡,以及强大的风险承受能力。特别指出的是,参加年金计划或员工福利计划等类年金的单位及广大参与人并不都具有强大的投资风险承受能力和丰富的财务管理知识,他们对待预期稳定的DB模式有强烈的需求,本文不过多地论述复杂的精算模型,而是从现金流量的视角出发,展示测算的模型,这更加易于认识与理解。
2 DB模式年金计划现金流量测算模型的构建
2.1 个人年金账户测算模型的构建
构建现金流量模型的关键点是测算出退休时点个人年金账户的积累总金额,它既是积累期的终值又是支付期的现值,受到各自期间的收益率水平、期限长短和年金缴费/支付水平的影响,首先需要准确测算。为简化论述并不失一般的情形,以下推导均假设以年度为周期,且在当年末完成年金的缴费或支付,DB模式的待遇支付金额是确定值。
(1)固定的退休待遇支付水平。设X0……Xn表示支付期内第n年末的年金账户余额,X0即退休时点年金账户的余额,Xn=0;年投资收益率r,支付年限n,每年在期末支付固定的待遇支付金额A。

归纳得式(1):
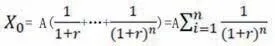
式(1)即为退休时年金账户中应积累金额的递推计算公式,即年金现值的计算过程,可通过查询年金现值系数表或利用Excel的PV公式求解。
(2)待遇支付水平每年按同比例递增。现实的经济环境中普遍存在通货膨胀。为抵消通胀预期的影响,计划参与人会期望年金计划作出每年递增支付养老金的方案。设退休首年支付的养老金为A,并以固定的增长率g每年递增。


归纳得式(2):

特别的,当g=0时,式(2)即简化为式(1);当g=r时,式(2)在运用等比级数求和公式得到的结果会出现分母为零而无法使用。式(2)可利用Excel编写自定义函数简便求解。打开Excel的VBA环境,插入模块并录入以下代码:
01 Function Recur(n As Integer,r As Double,a As Double)
02 Dim i As Integer
03 Dim sum As Double
04 sum=0
05 For i=1 To n
06 sum=sum+(1+g)^(i-1)/((1+r)^i)
07 Next
08 Recur=a×sum
09 End Function
其中n为年金年限,r为收益率,a为首年待遇支付额;01行声明了名为Recur的自定义函数,02~03行声明了计数变量与求和变量,04行初始化求和变量,05~07行通过一个循环体计算,08行输出函数求解值。
(3)测算出退休时点个人年金账户的积累总金额后,运用年金的现值和终值公式,即可测算该账户资产存量的序时分布。
2.2 年金计划层面的测算模型构建
分析了个人年金账户现金流量和资产存量的变动关系后,本节将个人账户的分析拓展到年金计划层面。年金计划中,无数个计划参与人的缴费起始点、年限、金额水平及退休时点都不尽相同,因此不同的年金计划的资产总体分布也会有所区别。将所有个人账户的现金流量(如表1、表2所示)和资产存量序时分布(如表3所示)有序汇总,就可以得到由所有参加者组成的年金计划的生命周期预测长度,以及计划层面生命周期内现金流量与资产存量的序时分布情况。其中资产存量序时分布有两种独立的算法思路,可相互印证计算结果的正确性,现金流量的序时分布由现金流量法得出。
(1)思路一:现金流量法。
第一,汇总整理所有参加年金计划职工的年龄、退休年龄、缴费金额、待遇支付金额、待遇支付期限等要素,计算退休时个人年金账户的积累总金额。第二,找出所有个人年金账户的积累总金额最大值,计算所需的最低缴费期,再加上待遇支付期,作为整个年金计划资产的生命周期。第三,在年金计划资产的生命周期内,将所有职工相应的缴费或支付现金流量序时填列,其中待遇支付以负数填列。第四,逐年分别求和现金流入量和流出量,二者相减得出现金净流量序时分布。第五,第i年末资产存量=(i-1)年末资产存量×收益率+期净流量。第六,循环迭代计算生命周期内所有年度的年末资产存量,得出资产存量序时分布结果。
(2)思路二:个人账户法。
第一、第二同思路一。第三,将每个个人账户的资产存量初始化为首年资产存量。第四,第i年末的资产存量=(i-1)年末的资产存量×(1+收益率)+i期现金流量。第五,汇总每一年所有的个人账户得出资产存量序时分布结果。
3 测算模型的实证分析
3.1 待遇支付期演算
以上述两种DB模式的个人年金账户支付方案展开演算。假设每年的投资收益率均为4%,且年度内收益率呈线性增长;支付期按17年估算(国家统计局2015年公布的人口平均寿命76.34岁)。方案一假设该个人账户每年末固定支付24000元(月均2000元标准),方案二假设首年末支付24000元,以后每年末支付金额按4%的增长率逐年递增。通过上述计算方法求得年金账户支付期的现值:方案一291976.05元,方案二392307.69元。该个人年金账户在不同方案下的变动对比情况如表1所示。
3.2 缴费积累期演算
支付期的现值即积累期的终值。为便于对比,假设积累期也在每年末进行年金缴费,且每年缴费额也为24000元。积累期的年金账户变动情况如表2所示。

表1 不同待遇支付方案情景下年金账户余额测算表(单位:元)
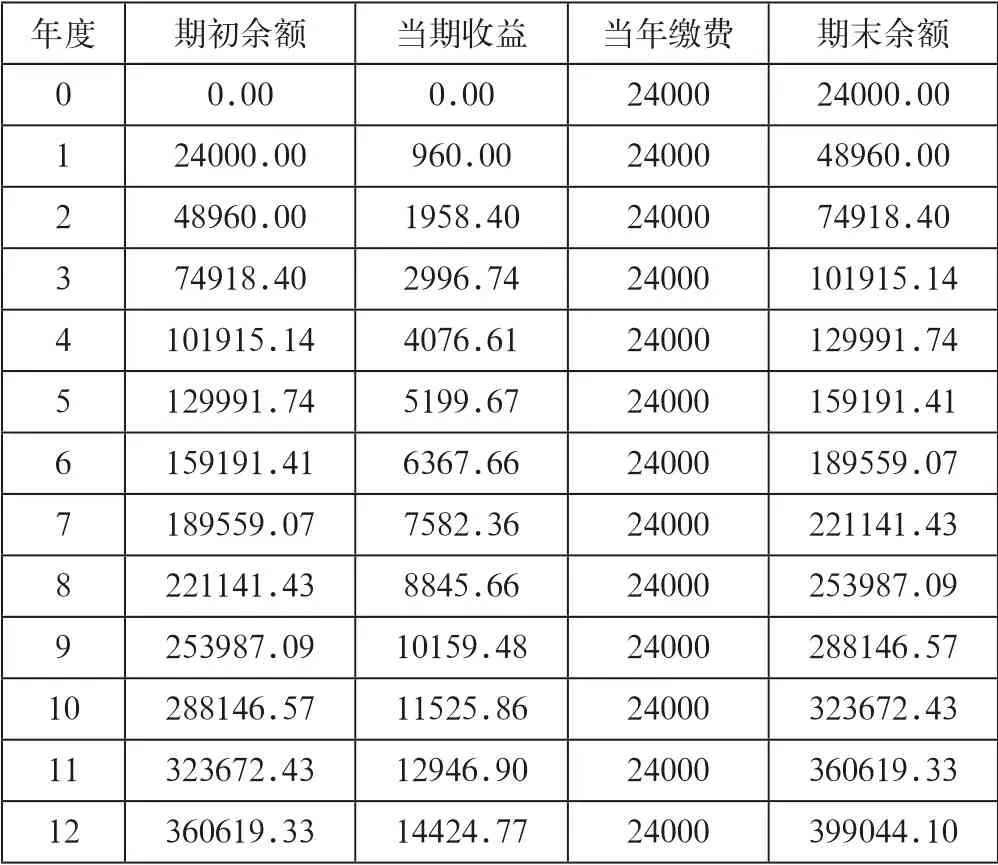
表2 年金账户在不同方案情景下的缴费测算表(单位:元)
不同的待遇领取方案下所需的最低年金缴费积累期分析如下。
方案一:第10年到第11年之间完成年金账户的积累,基于年内收益率线性增长的假设计算,需10.33年,即该账户最迟需在退休前10.33年开始缴费。
10+(291976.05-288146.57)/11525.86=10.33(年)
方案二:所需的积累余额392307.69元比第12年的期末余额399044.1元低6736.41元。所以在第12年的缴费后完成年金账户的积累。方案一与方案二的序时现金流量分布对比,如图1所示(注:积累期年度以负数列示,支付期以正数列示,下同。)。

图1 不同支付方案下年金账户现金流量对比
假设该年金账户达到所需积累额后立即开始养老金待遇支付。组合表1、表2可得方案一与方案二年金账户资产存量的时间序列表。
将表3的序时数据绘制成资产存量柱状图对比,如图2所示。

图2 不同支付方案下年金账户的资金存量对比柱状图
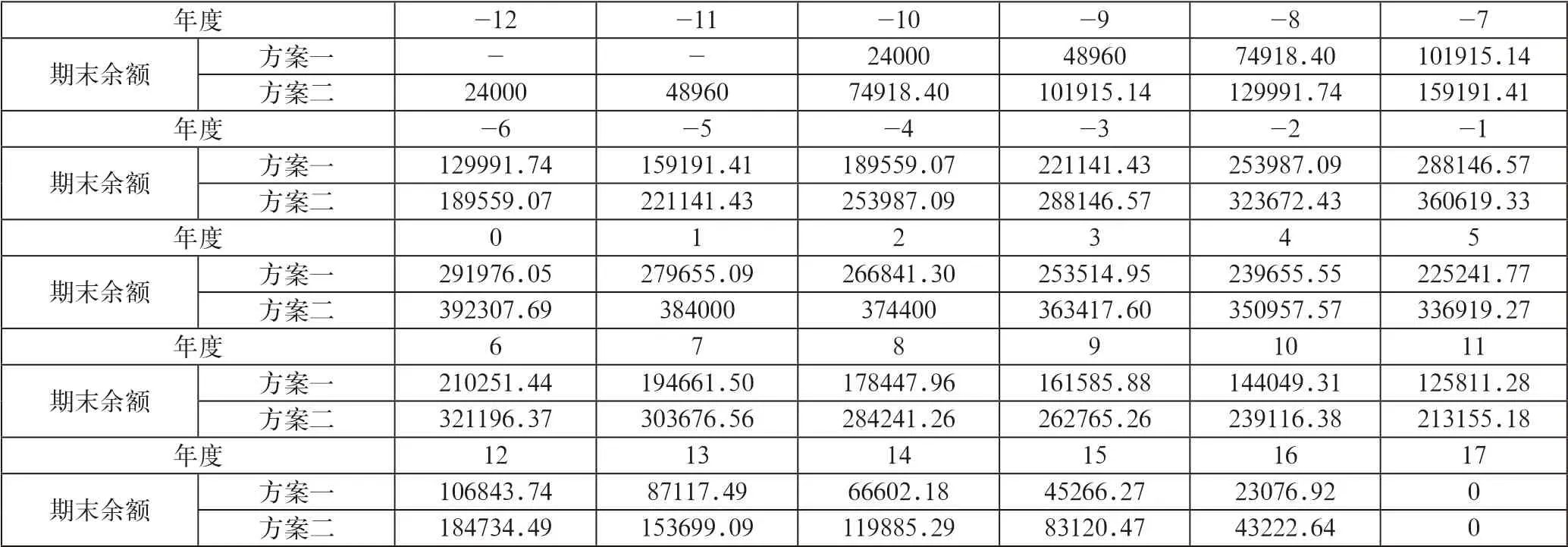
表3 年金账户资产存量时间序列表(单位:元)

表4 不同方案的经济指标统计表
以方案一为例进一步分析:缴费的本金总额24000×10=240000元;投资收益分为缴费积累期291976.05-240000=51976.05元,待遇支付期116023.95元,合计168000元。年金账户生命周期内本金总增值率168000/240000=70%,年平均收益率:

资产余额序时分布及各项经济指标统计可作为其他测算方案或业绩比较基准的参考,如表4所示。
4 研究不足与展望
4.1 缴费、支付周期的假设
出于简化模型分析的目的,本文假设年金计划的缴费和支付以年度为周期且都在年末进行。人社部36号令明确鼓励企业年金计划按月进行缴费和支付,熨平经济周期的波动性影响。另外,缴费时点也可能会在期初,在运用时应结合实际情况分析。
4.2 投资收益率难以准确预测
投资收益率是年金计划运营中重要也是最难预测的指标,因其受资本市场的影响波动较大,且一个年金计划下可能会有不同的投资组合,每个组合都有不同的投资策略、不同的资产配置,不同的投资标的,准确预测收益率十分困难,如表5所示。

表5 近五年全国企业年金基金投资收益率统计表
数据来源:人社部历年《全国企业年金基金业务数据摘要》;2018年度数据尚未公布。
4.3 动态分析的研究方向展望
本文所论述的年金计划层面现金流量与资产存量分析研究对象,是计划建立时点的所有参与人所构成的样本空间,因此研究方法是一种相对静态的方法。进一步的,如能再将后续的人员新增因素考虑进来,将不同年度所预测的现金流量和年金存量资产再次叠加,就可以得出现金流量和存量资产的动态分布情况,但这需要更加准确的原始统计数据、更加科学的预测手段和大数据处理能力,也是未来可以展开深入研究的一个课题方向,本文不再展开叙述。

