基于模糊纯追踪控制的自动泊车算法研究

陈 龙，罗 杰，杨 旭，王小龙

(1.武汉理工大学 自动化学院，湖北 武汉 430070；2.中国船舶重工集团公司第七二二研究所，湖北 武汉 430205)

近年来，汽车保有量在迅速增长，城市车位十分狭小，泊车让大量驾驶员感到困惑。泊车辅助也应运而生，现阶段倒车影像、全景环视系统逐渐普及[1]，但是仍需要驾驶员完成泊车工作。自动泊车系统无需人工干预，能够快速、安全地使车辆驶入泊车位，可有效帮助驾驶员解决泊车问题。因此自动泊车系统的开发也成为汽车主动安全研究的重要方向之一，有着很好的应用前景[2]。

自动泊车系统一般由感知系统、决策系统和控制系统3部分构成。感知系统通过超声波雷达[3]、激光雷达、摄像机[4]等传感器获取可用泊车位信息。在此基础上，决策系统根据车辆固有的物理约束条件和碰撞约束条件，生成一条合理的泊车曲线。控制系统通过实时控制车辆的车速和转向角，达到对泊车曲线的跟踪，完成泊车操作。现阶段自动泊车的研究重点是泊车的路径规划与追踪控制。

在路径规划方面，两段最小转弯半径的圆弧组成的两段式泊车路径可使需求泊车位最小，易于开发，但是在两圆弧相切位置，曲率发生了突变，需要车辆在该点停车转向，会加大对轮胎的磨损。为此，学者们对两段式路径进行了优化与改进。如穆加彩等[5]使用一种基于三阶多项式与反正切函数的路径拟合方式，使曲线与两段式泊车路径相仿，改善了曲线曲率的连续性。李红等[6]基于B样条理论，选取多个特征点作为泊车曲线的固定点，通过动态调整曲线的阶数，使泊车路径曲率连续。但是使用高阶拟合或者动态多点计算的方法加大了计算量，考虑到工程适用性，笔者在两段式泊车路径上，使用回旋曲线进行优化，解决两段式路径曲率突变问题的同时降低计算量。

在路径跟踪方面，纯追踪算法因其模型简单，参数易调的特性，广泛应用于智能车路径跟踪研究。其中，前视距离这一主要参数的整定极大地影响了路径跟踪效果。段建民等[7]根据横向偏差来调整前向距离，使运动轨迹平滑，避免了横向误差较大时，转角控制量突变的情况。唐小涛等[8]综合考虑车辆速度与横向偏差，设计模糊控制来自适应调整前视距离，增强系统对速度的适应性。黄沛琛等[9]使用BP神经网络实现前视距离的动态调整，仿真证明该方法对车辆转向调头的曲线跟踪效果良好，且无震荡现象。但上述研究目标路径设计较为单一，且没有结合航向偏差来设计合适的控制算法，导致对不同误差输入及目标路径的跟踪效果相差较大，难以适应由多种曲线生成的泊车路径。为此，笔者对纯追踪模型进行改进，通过模糊控制，融合航向误差与横向误差，进而动态调整前向距离，并应用在泊车系统中。

1 泊车路径规划

1.1 车辆运动学模型

对于前轮转向车辆，后轴与车身的运动轨迹一致，因此将后轴中心作为车辆参考坐标。车辆泊车时处于低速状态，忽略侧向力的作用，车辆不会出现滑移与侧向移动的状态。基于阿克曼转向机构的车辆运动学模型[10]如图1所示，关系式如式(1)所示。

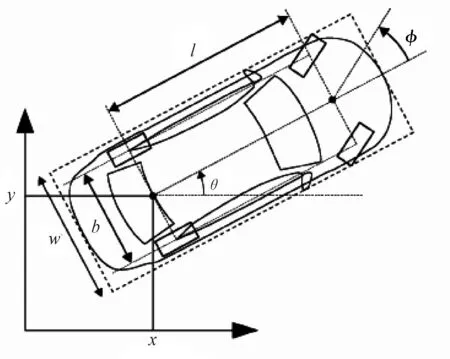
图1 车辆运动学模型

(1)

式中：θ为车辆航向角；φ为等效前轮转向角度；v为车辆纵向速度；l为车辆轴距；x,y分别为车辆后轴中心的横纵坐标。在任何时刻，瞬时转向轨迹与车体线速度方向相切，对应的后轴中心点的运动轨迹如式(2)所示。

(2)

其中，r为瞬时转向半径。由此可得：汽车低速泊车时，其运行轨迹是一段圆弧，且圆弧半径与车速无关，而与转向角度和轴距相关，这为轨迹规划提供了理论依据。

1.2 基于回旋曲线优化的泊车路径规划

回旋曲线是随着曲线长度增加，曲率线性变化的一类曲线[11]，回旋曲线示意图如图2所示。若车辆行驶时具有恒定的纵向速度同时保持前轮转角变化率一定，车辆后轴中心的运动轨迹即是一条回旋曲线，可以保证行驶曲率的连续性。基于上述性质，使用回旋曲线对两段式泊车路径进行优化，既有利于后续的跟踪控制，又能解决切点处曲率突变问题。

图2 回旋曲线示意图

在P点处曲率半径为R，O点处曲率为零，则P点坐标及在P点处的航向角分别为：

(3)

VOROBIEVA等[12]使用上述性质，建立了适用任意初始位置的双圆弧路径，并使用了4段固定的回旋曲线将双圆弧的两侧进行连接，实现曲率连续、满足车辆运动学的泊车路径。考虑车辆约束条件和回旋曲线的性质，一般加入的回旋曲线长度约为0.5m，相比于双圆弧路径，会显著增加需求车位的长度。为了适当减小需求车位长度，笔者使用两段对称的回旋曲线连接两段圆弧，并将设计的曲线序列作为泊车路径，如图3所示。

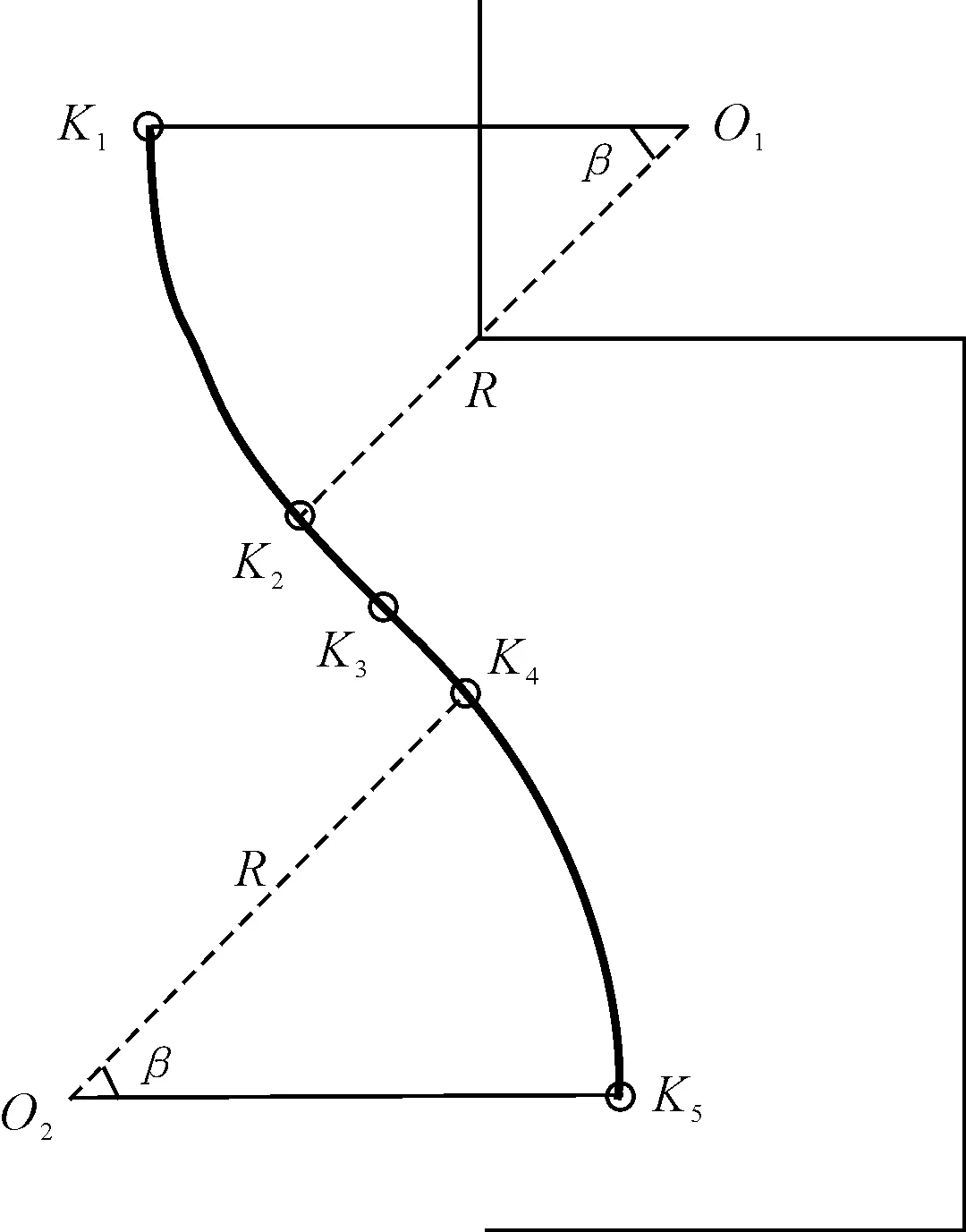
图3 规划路径示意图

路径起始点为K1，目标点为K5，由传感器获取位置。K1K2段，车辆转角处于最大值；K2K3段是曲率由最大变化到0的回旋曲线，后半段曲线与前半段以K3为中心对称。

由起始点到终止点的坐标变化量计算得到起始点纵坐标YK1及两段圆弧圆心角β：

(4)

式中：lr为后悬长度;w为车辆宽度；D为车辆与车位的距离，由感知系统获取。至此，路径的各段曲线长度及关键点均可由式(3)和式(4)求出。

2 路径跟踪控制器设计

对于泊车系统而言，为了跟踪规划的泊车路径，车辆的后轴中心坐标(x,y)需要快速趋近目标曲线，同时车辆的航向角θ也要与曲线各点的斜率保持一致。鉴于多个目标量同时控制的复杂性，笔者采用纯追踪的控制方法，通过车辆运动时的几何关系将受控量进行降维，简化泊车路径跟踪模型。

2.1 纯追踪模型的建立

在实际泊车系统中，控制器周期性地从传感器接收信息，计算并发送控制量给执行机构，所以必须对车辆运动学模型(式(1))进行离散化处理：

(5)

式中：(xn-1,yn-1,θn-1) 为第n-1个采样周期时车辆的位姿状态；(xn,yn,θn)为第n个采样周期时通过更新的车辆位姿状态；Δsn为车辆在第n-1个采样周期到第n个采样周期间行驶的距离，一般由后轮轮速脉冲传感器得到。当车辆起始航向角已知的情况下，根据式(5),由转角反馈量和轮速脉冲传感器的信息推算出后轴中心的位置坐标(x,y)及车辆实时的航向角θ。基于推算的车辆状态及规划的目标曲线，便可设计控制算法。

以直线的目标路径为例，纯追踪模型示意图如图4所示。其中：O为瞬时转向圆心；R为转弯半径；Ld为预定前视距离；p为横向距离，代表车辆目前与目标路径最近点的距离；γ为圆弧CD对应的圆心角。

图4 纯追踪模型

在车辆行进过程中，根据固定的前视距离Ld在目标路径S上找到唯一对应目标点D作为预瞄位置，圆弧CD即为理论运动路径，通过控制车辆跟随理论转向角度，从而运动到指定路径S上。根据几何关系可得：

(6)

根据式(6)计算可得：

(7)

从而得到目标等效前轮转角：

(8)

根据几何关系，纯追踪模型将路径的追踪转换为对目标点的追踪，通过控制前轮转角，快速减小位置误差，同时逐渐减小航向误差。

2.2 模糊纯追踪控制器的设计

由式(8)可知，前视距离Ld是纯追踪控制模型唯一可调参数，决定了控制效果的优劣。一般而言，大的前视距离适合直线工况，跟踪时间变长，不能完全跟随路径的细节；小的前视距离适合曲线工况，使车辆迅速地跟随曲率较大的目标轨迹，但参数选择过小会引起震荡。由于泊车路径由多段曲线构成，且曲线特性随车型参数而发生改变，单一的前视距离不能满足复杂的泊车工况。因此，利用横向距离p和航向角度误差θe来反映车辆与目标点的位置偏差与角度偏差，将其设置为模糊控制器输入，动态改变前向距离以达到对复杂路径的适应性。控制系统框图如图5所示。

图5 控制系统框图

转向角偏差、横向距离偏差及输出前视距离均分为7个模糊集合，横向距离取[-40，40](cm)，航向偏差取[-90，90](°)，前视距离取[0.2，1.0](m)。以曲线左侧横向偏差为正，右侧为负；航向偏差顺时针为正，逆时针为负。建立模糊规则的原则为：①航向误差较大时，快速减小前视距离，使车辆方向快速与曲线达到一致，进而减小位置误差；②横向误差在逐渐减小时，关注系统的稳定性，适当增大前视距离，防止系统震荡。综合考虑横向距离和航向偏差不同情况下的重要性，构建前视距离输出模糊规则，如表1所示。

表1 前视距离为输出的模糊规则表

3 仿真与分析

3.1 路径规划仿真

使用仿真车辆为江淮iev7s，实验车辆参数如表2所示，在MATLAB GUI中根据规划方法进行仿真，检验路径规划的可行性。

路径规划仿真结果如图6所示，最小车位长度为6.2 m，最小车位长度与车长比值为1.50。文献[12]使用的仿真车辆的车长为4.084 m，单次泊车最小泊车位为6.8 m，比值为1.67。笔者规划的泊车路径使用了回旋曲线，保证了泊车过程的曲率连续，并且在一定程度上减小了需求车位长度，泊车终止坐标处车辆与车位平行，路径平滑，达到路径规划的目标。

表2 实验车辆参数 m

图6 路径规划仿真结果

3.2 路径跟踪仿真

泊车路径会随车辆参数的不同而发生调整，且在寻找车位的过程中，车辆的直线运动也是受泊车系统控制，故仅使用单一的泊车路径对控制算法进行验证是不够的。一般使用直线、正弦曲线等路径对跟踪控制算法进行验证是比较有代表性的，可以客观地评价算法对路径跟踪的响应速度、跟踪误差等指标。仿真中车速均设定为5 km/h。

3.2.1 直线路径

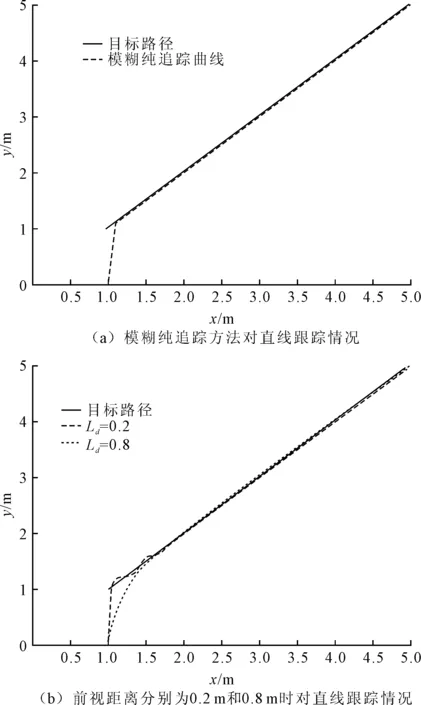
图7 对直线路径跟踪情况

由图7(a)可知，模糊纯追踪方法在x=1.2以后误差趋于稳定，能快速减小误差，且轨迹较为平滑。由图7(b)可知，Ld=0.8 m的纯追踪方法收敛速度稍慢，略微超调后，能很好地跟随直线的工况；Ld=0.2 m时响应速度最快，但是会产生震荡，达到稳定的时间过长。

3.2.2 正弦曲线路径

图8 对正弦曲线路径跟踪情况

3.2.3 回旋曲线优化的两段式泊车路径

图9 对泊车曲线跟踪情况

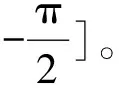
车辆模型泊入车位仿真如图10所示，可知基于模糊纯跟踪控制的方法在起始位姿有较大误差时可以很好地实现对泊车路径的跟踪，让车辆无碰撞地泊入车位。

图10 车辆模型泊入车位仿真

综合以上情形可以看出：使用模糊纯追踪控制算法在多种工况下均能有效跟随目标路径，误差较小，可以满足泊车的要求，有较好的稳定性。

4 结论

针对两段式泊车曲线曲率不连续的缺陷，使用回旋曲线对其进行优化，给出路径计算方法，并通过仿真验证了该泊车路径的可行性。对于路径跟随模型的复杂性，使用纯追踪模型可将路径追踪模型简化。由于纯追踪模型前向距离是一个固定值，无法很好跟随复杂的泊车路径工况，设计了模糊控制器来实现前向距离的动态调整，通过仿真验证了该算法在指定泊车路径跟踪的可靠性，有效改善了泊车系统的泊车精度。同时,对直线及正弦曲线等目标曲线追踪进行测试，证明了该路径跟踪方法有一定的道路自适应性。