基于分块sim-min-Hash的近似图像检索

刘 翔 宇

(北京大学软件与微电子学院 北京 116024)

0 引 言

基于内容的图像检索技术[1]CBIR突破了传统基于文本的图像检索TBIR所造成的工作量大量性和主观注释信息不稳定性的瓶颈，大大提高了图像资源的利用率，为使用者提供了全新的体验。基于内容的图像检索技术这一概念于1992年由T.Kato提出[15]。他在论文中构建了一个基于色彩与形状的图像数据库，并提供了一定的检索功能进行实验。近似图像被定义为对于同一物体或场景，在不同的拍摄情况(遮挡，位移，光线变化，背景，色差)下获取的图像，是CBIR重要检索对象之一。根据文献[16]可知，互联网20亿幅图像中，有22%存在近似图像，而且8%的图像拥有超过10幅近似图像。

而基于内容的搜索引擎的出现以及查找具有版权问题的未授权图像的需求和一些分析类的场景对近似图像检索的科研需求愈来愈高[14]。另外，近似图像检索技术对于传统的基于内容检索技术同样大有裨益。例如，近似图像是基于倒数最近邻[17]或数据库扩充技术[12]的搜索技术的先决条件。

近似图像检索的整个过程大致分为如下几个步骤：

(1) 对图像集进行特征提取，如使用SIFT算法[2]等。

(2) 对提取的特征点进行聚类，如K-means[3]等方法。

(3) 生成Bag-of-Words模型描述图像信息。

(4) 利用相关算法进行图像相关性的计算。

Min-Hash算法是一种经典的算法，Chum等在2008年BMVC中将min-Hash应用于近似图像检索中[16]。2013年由赵万磊和Hervé Jégou等在ACMMM2013提出了基于min-Hash算法的改进算法sim-min-Hash算法[4]，提高了图像检索的准确性。

本文基于sim-min-Hash算法继续进行改进，引用了分块机制，提出了分块sim-min-Hash算法。

1 min-Hash算法

1.1 Jaccard相似度

比较两个集合相似度的时候常用到Jaccard系数[5]，即对于给定的集合A和集合B，A、B中公有的元素个数占A和B的总元素个数的比重：

1.2 min-Hash算法

min-Hash算法是加速计算Jaccard相似度的一个很好的算法。尽管对于准确性上，min-Hash算法有一定的损失，但是min-Hash这种算法却可以大大地减少计算Jaccard相似度所耗费的时间[6]。

min-Hash的原理为，假设存在两个集合A、B,将集合A、B中的元素经过哈希函数转换后，如果其中具有最小哈希值的元素如果既在A∪B中也在A∩B中，那么hmin(A)=hmin(B)，集合A和B的相似度就可以表示为集合A、B的最小哈希值相等的概率，即：A和B的相似度就可以表示为集合A、B的最小哈希值相等的概率，即：

J(A,B)=Pr[hmin(A)=hmin(B)]

而min-Hash算法应用在近似图像检索中，就是先对对图像进行特征提取，聚类，生成词袋模型后，再进行min-Hash的计算，来计算出图像的相似程度。

在工程实践中，常常引入sketch作为新的计算对象来进行计算，起到加速计算的目的。

如果把几个哈希值合而为一，再进行运算，那么就会起到加速的作用。我们把几个哈希值合而为一的产物就是sketch。

2 sim-min-Hash算法

min-Hash算法的核心思想就是将所提取的图像的特征值(一般用Bag-of-Words来表示)进行哈希变换，然后通过对于通过哈希变换所得到的一系列值进行相关处理，来比较图像的相似性。

这种将图像提取特征，将图像特征进行再变换，然后再进行比较的方法，由于在提取图像特征值的过程中已经损耗了一定的对于图像特征的表示的信息量，而且再度进行哈希变换过程中，又不可避免地损耗掉了一定的信息量，对于图像比较相似度的精确度，肯定会有一定的影响。

而在min-Hash算法运算的过程中，最关键的一步就是只是找到最小哈希值进行Jaccard距离的计算。那么如果对于后续的过程中，我们不使用哈希值来运算，而是使用进行哈希变换前的原值进行运算，而哈希变换只是提供了寻找能得到最小的几个哈希值的原值的手段。由于原值包含的信息量和进行哈希变换后所得到的信息量相比更大，更能代表图像的信息，如果用这种方法，精确度可以得到提升，但运算的时间复杂度却并没有增加。

基于这种思想，sim-min-Hash算法应运而生。简单来说就是在min-Hash算法的具体操作中用原值代替了哈希值来组成sketch来进行运算。

3 分块sim-min-Hash算法

3.1 分块sim-min-Hash的算法思想原理

根据对于大量近似图像的观察，近似图像中的近似部分往往都具有一定的集中性，相似部分大多只是分布于图像的某一区域，而不是散布在整幅图像中，或者是占据整幅图像。

由此，发现如果对图像进行分块化处理(图1(a))，则可大大降低特征点被sim-min-Hash的次数，从而提高算法效率。而且，分块还可以将图像网格化，通过查找相似网格可以实现对近似目标的定位，大大增强了检索的应用范围。

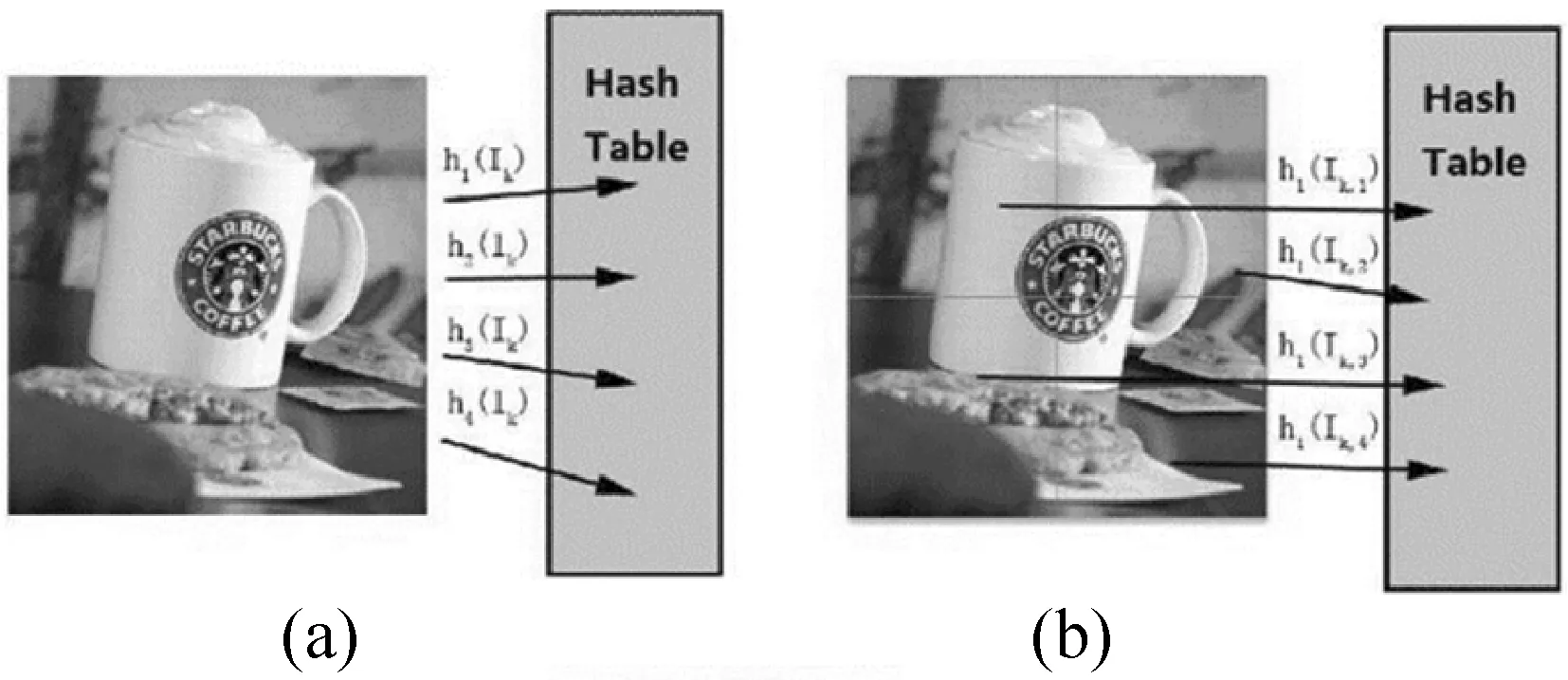
图1 分块sim-min-Hash算法原理

基于这种思想，提出了分块sim-min-Hash(Partition sim-min-Hash，PsmH)这种新型的算法( 当然也可以对min-Hash进行分块处理，但处理的效果显然不如对于sim-min-Hash算法进行分块处理，因为sim-min-Hash算法本身就已经是对min-Hash算法的一种优化)。但是，由于分块可能会将近似区域失去完整性(图1(b))，因此采用了块重叠技术来提高近似部分被分块完整覆盖的概率，并由此提高了检索的准确性，如图1(c)所示。块重叠技术可以将图像分为许多小的网格，然后通过合并相似的网格作为同一分块来达到分块完整覆盖近似部分的目的。

实验结果证明，PsmH在查准率、查全率和速度方面都大大强于min-Hash以及sim-min-Hash。并且PsmH更加容易实现，只要在sim-min-Hash算法的基础上，增加分块大小和重叠门限两个参数的设置即可。

3.2 PsmH算法来比较图像相似性的实现过程

设一共有i幅图像，首先将每幅图像被分为p个相等的矩形区域(p1,p2,…,pp)，每个区域就被称为一个分块。然后，对每个分块分别进行提取SIFT描述子，并对所有SIFT描述子集合，进行K-means聚类，而不是像sim-min-Hash一样在整幅图像中提取SIFT描述子。根据聚类结果，分别对每个分块独立生成Bag-of-Words模型。再对每个分块独立进行sim-min-Hash，组成在sim-min-Hash下的sketch，将结果存入Hash表中。

然后分别比较不同图像间不同分块的冲突概率，如果大于某一设定的门限，则可判定这两个分块相似。最后通过比较不同图像间拥有相似分块的数目来判断这些图像的相似性。

3.3 块重叠技术

要进行分块sim-min-Hash，第一步一定要进行块重叠的判定。

如果图像I1中的两个相邻分块p1、p2都与图像I2中的分块p3相似，即可认为p1、p2共同描述了I2和p3中的特征。

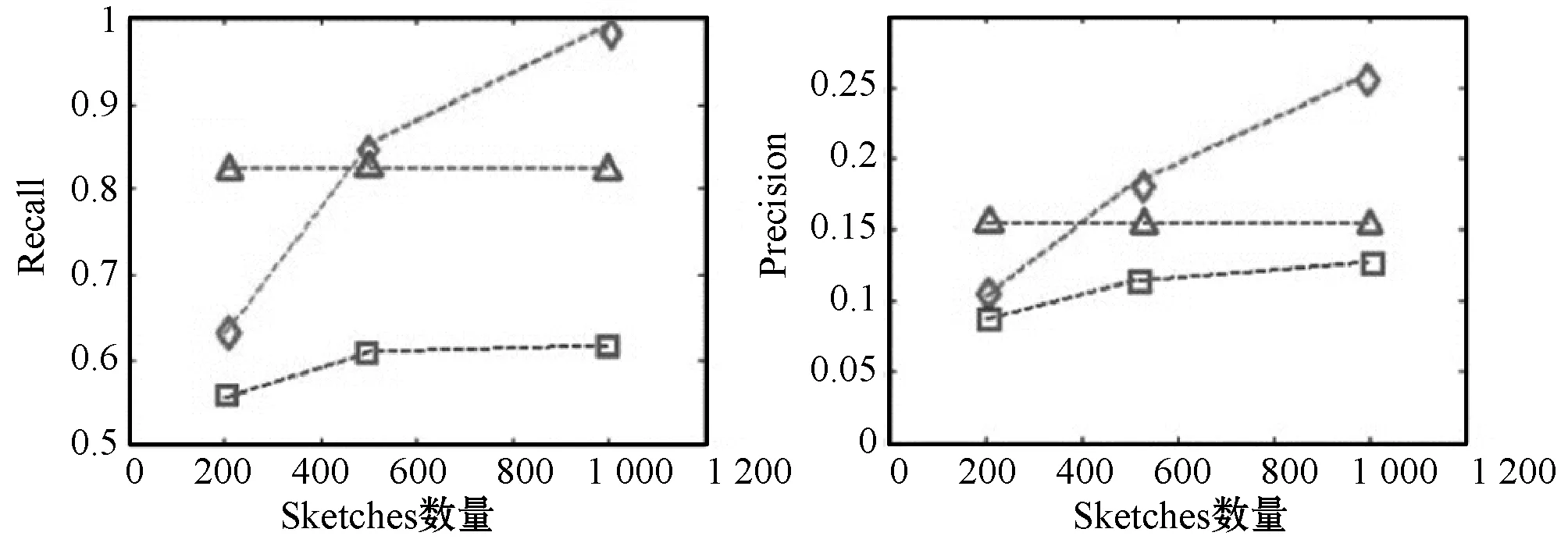
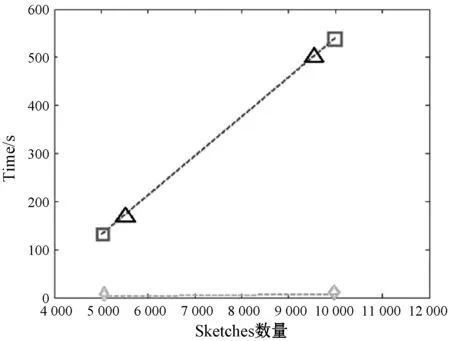
但是，值得注意的是，由于此时是为了查出更多的相似块，而不是对不同分块进行筛选，因此我们应该设定新的较小的不同于T1的相似性门限T2，即T1

3.4 目标定位技术

为了使待检索目标能够被更准确地识别，减少背景特征的干扰，因而需要保证定位环节在以确定的同类图像间执行。当然，如果只有少量的干扰图像，那么对结果也不会产生过大影响。

首先通过PsmH查找出相似的分块，由于待检索图像都已确定属于同一类，即包含同一类相似特征，因此待检索特征的出现概率应该最大，然后可以对输入检索图像中相似块的进行出现概率排序来过滤出最需要的检索目标。

例如，在图2(a)第一列中，只有含有星巴克商标的分块在不同图像中多次近似出现，它的出现概率最大，因而可以将它筛选出来，如图3(a)所示。当然，背景特征由于具有多样性也可能会产生很大的出现概率，进而影响定位结果，如图3(b)所示，但是这种影响可以通过多次运行来进行消除。

(a) 自建库 (b) 牛津建筑图2 检索出的近似图像对

图3 用PsmH方式定位结果

4 PsmH的优势分析

4.1 时间效率的优势分析

在讨论时间效率上，首先我们要知道在算法的运行(尤其在工程实践)中，时间都耗费在了什么地方：

运行时间主要分两部分：(1) 生成sketch的时间，其中包括Hash方程建立时间和min-Hash值计算时间；(2) 其他前期操作的时间,如从磁盘读取数据的时间、提取SIFT描述子的时间、K-means聚类的时间、Bag-of-Words(或Set-of-Words)模型生成的时间和建立Hash表的时间等等。

而在sim-min-Hash和PsmH两种算法中，由于图像总量和每幅图像中提取的sketch数量相同，因此前期操作时间基本一致，所有主要时间差距主要体现在sketch的生成环节上。

由于PsmH只是选取了一部分分块来进行运算，在生成sketch的过程中，需要进行操作的原始数据本身就少了，所以PsmH的时间效率显而易见地更高。

4.2 查全率和查准率的优势分析

下面将要分析分块sim-min-Hash生成的sketch比min-Hash和sim-min-Hash具有更强的识别力的原因。并且通过分析真近似图像对和伪近似图像对的冲突概率，对查准率(Precision)和查全率(Recall)进行评估。

查全率主要由真近似图像对的冲突概率体现，定义为返回值中的真近似图像对的数量比上真近似图像对的总数。查准率和伪近似图像对的冲突概率相关，但不相等，定义为返回值中的真近似图像对的数量比上返回图像对的总数量。

PsmH提高了真近似图像对的冲突概率和降低伪近似图像对的冲突概率，因而具有更高的查准率和查全率。

首先，分析真近似图像对的冲突概率。为了简化分析过程，先不考虑块重叠的情况。近似部分在分块中的位置可以分为三种情况，如图1所示。在分析中，假设所有特征点都均匀散布在整幅图像中，并且同一幅图像的每个分块中含有等量的特征点(包括成对和不成对出现的背景特征)。

我们可以通过如下四种情况进行比较分析：

情况1：近似特征全部集中在一个分块中；

情况2：近似特征分布在不同分块中；

情况3：近似特征只集中于一幅图的一个分块中，而分散在另一幅图的所有分块中；

情况4：伪近似图像对的冲突概率假设在伪近似图像对中，两幅图像的近似特征随机分散在图像中，而不是集中在特定分块中。

通过实验可以证明，无论这四种情况中的哪种情况出现，在查全率和查准率方面，都是PsmH更具备优势。

5 实验结果与分析

5.1 实验数据

使用牛津建筑库来进行实验，如图4所示。牛津建筑库中包含5 062幅从FLICKR下载的牛津地标性建筑，图像尺寸大约为1 000×1 000，对每幅图像提取大约2 500个SIFT特征点，并使用K-means进行1 000个中心的聚类。同样由于数据库过于庞大，无法对全部图像进行测试，因而随机选取了其中的552幅图像，并且将其分为14类进行检索。

图4 牛津建筑库

5.2 结果分析

依据经验，对牛津建筑库中的图像进行了分块数从16～81块的测试，实验结果证明，当分块数为25的时候，PsmH的效果最好，因为此时近似特征被单一分块完整覆盖的几率较大，还可以减少背景元素的干扰，定位的效果也很好。依据不同的sketch数量，min-Hash的门限T会随之变化，以突出近似部分的重要性。根据实验数据，当每个sketch中min-Hash数量k=2时，Hash在准确度和速度上得到最佳均衡，因此在测试中，保持k=2不变，来考察sketch的数量n=200、500、1 000变化时，PsmH和sim-min-Hash相对于min-Hash在查准率、查全率和速度上的提升。

在查全率方面，通过实验，当sketch数量n=200时，PsmH的查准率为0.629 2，相对于min-Hash的0.554 6有13.5%的提升，但是仍落后于sim-min-Hash的0.823 4，如图5所示。

(a) Recall (b)Precision图5 自建库在固定sketch数量下的运行结果(□代表min-Hash，△代表sim-min-Hash，◇代表PsmH)

当n=500时，PsmH的查全率相对于n=200时自身有了35.6%的提高，达到了0.853 1，相对min-Hash提高了40.2%，而且超过了sim-min-Hash。sim-min-Hash虽然落后于PsmH，但相对于min-Hash仍有35%的提高。而min-Hash虽然也有一定提高，但是幅度大大小于PsmH。当n=1 000时，PsmH在查全率的优势达到峰值，比同条件下min-Hash提高了60.9%，同时高出sim-min-Hash 20.6%。sim-min-Hash高于min-Hash 33.4%。

当n=500时，PsmH的查准率相对自身提升有了75%的大幅提升，超过同条件下min-Hash 60.9%，并且超过sim-min-Hash。此时，sim-min-Hash仍高出min-Hash 35.7%。当n=1 000时，虽然min-Hash的查准率有一定提升，但是仍落后于sim-min-Hash 20.8%，仅仅是PsmH的49%。

可以看出，n在200～1 000范围内，PsmH和sim-min-Hash在查准率方面相对于min-Hash都有较大的提升。当n比较小时，应该选择sim-min-Hash。而随着n的增长，PsmH的优势迅速扩大。主要是查准率和伪近似图像对的冲突概率相关，如前文分析的一样，PsmH和sim-min-Hash都提高了真近似图像对的冲突概率并降低了伪近似图像的冲突概率，因而查准率相对于min-Hash大大提高，与理论分析一致。

为了比较Psmh运算速度的优越性，并且说明n值增加对速度的影响，专门从牛津建筑库中选取了15幅图并对其进行中心数量为300的K-means聚类，然后进行sketch生成速度测试。结果表明，如图6所示，min-Hash与sim-min-Hash的速度基本相同。而当n增加到5 000时，sim-min-Hash耗时131.276 468 s，而PsmH为2.577 719 s，仅为sim-min-Hash的1.96%。当n进一步增加到10 000时，PsmH耗时7.481 789 s，而sim-min-Hash为541.257 151 s，PsmH仅为sim-min-Hash的1.38%，速度提升72.6倍。因此可推断，随着n的增加，PsmH带来的速度优势会越来越明显。

图6 当n=5 000到n=10 000时，PsmH和sim-min-Hash、min-Hash速度对比(□代表mH，△代表sim-min-Hash，◇代表PsmH)

6 结 语

本文对min-Hash算法和sim-min-Hash算法进行了改进，提出了分块sim-min-Hash(PsmH)算法，从而获得了更高的查准率和查全率。分块sim-min-Hash利用了近似特征在近似图像中区域性分布的特点，将图像分块化处理，对每一个分块独立进行sim-min-Hash变换，进而提高了真近似对的冲突概率，降低了伪近似对的冲突概率，在三种方法中拥有最高的查准率和查全率。其中，在牛津库的测试中，PsmH平均查准率相对sim-min-Hash最大提升107%，而平均查全率最大提升57.4%。块重叠技术的引进使得分块sim-min-Hash的效率得到了进一步提高。而且分块sim-min-Hash大大降低了所需Hash方程的数量和sketch生成的时间，当sketch数量巨大时，速度提升效果明显。