高等数学绪论课的教学策略与实践
侯彩霞
(广州南洋理工职业学院,广东 广州 510925)
绪论是一门课的先导,是课程的纲领,是教材的浓缩和内容的引领。绪论课是学生学习一门新课程的指南,是建立新课程整体观念的起步,能为学生回答“为什么学”“学什么”“怎么学”三个基本问题。同时每一位学生都渴望任课老师是一位学识渊博、谦逊有礼、思维缜密、乐观进取、讲授有方的人。每一位高校教师都应该为学生上好第一课而精心设计、巧妙引入。良好的开端意味着成功的一半,如果上好了绪论课,能把握并利用好学生的求知心理,激发学生的学习兴趣,培养学生的数学素养,使他们怀着期待信心满满地投入到这门课程的学习,可以收到事半功倍的效果。为使学生从初等数学快速顺利地过渡到高等数学的学习中,更好的使用好数学,来解决各自专业中遇到的实际问题,成长为高素质的人才,越来越多的教师不断探索绪论课的教学模式、讲授策略、教学艺术等[1-4]。
“高等数学”是高等教育中的一门重要公共基础课,大学教育中的其他数学课程以及专业课程几乎都与高等数学相关,它以微积分为核心,体系完整,应用广泛,在培养学生抽象思维、逻辑能力和创新意识上起着举足轻重的作用。所以,如何在学生进入大学后,学习高等数学课程的开始,就给学生以全面、准确、有效的引导,以期让学生了解本课程的发展、内容、思想、方法、意义、应用等,并产生浓厚的学习兴趣,成为绪论课的重要任务,因此,在教学中,从以下几方面对绪论课展开了探索与实践。
一、巧妙引入,励志教育
在课堂开始,抛出这样一个数字游戏,易知,1365=1,问题1:请同学们猜一猜“1.01365=?”“0.99365=?”。学生的答案几乎都是与1差不多大小的数。这时,出示结果“1.01365≈37.7834,0.99365≈0.0255”,该答案与学生的猜测相距甚远,引起学生思维的碰撞,激发学生的兴趣。教师接着抛出问题2:这其中蕴含了什么道理,开始学生并无头绪,教师加以引导,提示“如果1代表原地踏步,365代表一年的天数”,这时学生容易体会出这样的道理:积跬步以致千里,积怠惰以致深渊。为了加深理解,教师给出“1.02365≈ 1377.4,0.98365≈ 0.0006”,引导学生体会出:“只比你努力一点的人,其实已经甩你很远”,这与“积土而为山,积水而为海”有着异曲同工之妙。这时,教师激励学生,新的学期开始了,大家每天多努力一点点,一年后肯定能有很大的进步与提升,努力遇见更好的自己,此时,学生信心百倍,充满兴趣,开始新课程的学习。
二、历史介绍,提升认识
读史可以明智,对学习一门课程来说,亦是如此。学生从小学阶段就开始学习数学,并且数学在人生的重要转折点都起着关键的作用,简要介绍数学的发展史,帮助学生了解为什么要继续学习数学,学习什么内容,数学的发展程度等问题,起到引领作用,提升学生对数学的认识。
数学的发展可以归结为以下几个阶段。数学的萌芽时期:远古时代至公元前6世纪,这一时期的数学知识是零碎的,没有命题的证明和演绎推理。常量数学时期:公元前6世纪至17世纪上半叶,具有比较系统的知识体系、比较抽象的并有独立的演绎体系的学科。中国古代数学名著《九章算术》和古希腊的《几何原本》是代表作。现在中学数学课程的主要内容基本上是这一时期的成果。变量数学时期:公元十七世纪上半叶至十九世纪二十年代,迪卡尔的解析几何学、牛顿-莱布尼茨的微积分及围绕微积分理论和应用而发展起来的一大批数学分支,使数学进入了一个繁荣的时代。近代数学时期:十九世纪二十年代至二十世纪四十年代。微积分基础的严格化、近世代数的问世、非欧几何的诞生、集合论的创立都是这一时期的成就。空前的创造精神和严格化是其主要特点。现代数学时期:二十世纪四十年代至现在。以数学理论为基础的计算机的发明使数学得到空前广泛的应用。泛函分析、模糊数学、分形几何、混沌理论等新兴数学分支产生,这些理论已进入大学高年级及研究生的学位课程中。
三、内容思想,比较分析
高等数学的基本内容为微积分学。微积分学是高等数学的核心,研究函数的连续性、可微性、可积性等分析性质。
高等数学与初等数学的主要区别在于研究的对象和研究方法的不同;初等数学主要研究规则、平直的几何图形和均匀、静止的、不变的、有限过程的常量;高等数学主要研究不规则、弯曲的几何对象和非均匀、运动的、变化的、无限过程的变量。图1以图形对照的形式说明二者的区别和联系。

图1 初等数学与高等数学区别示例
微积分的出现,可以解决许多上述及其他应用初等数学的知识无法解决的问题,大大推动了科技的进步及数学理论的发展,高等数学比初等数学更加全面,更加深刻,更加细微,更加本质,更加理论化,更加系统化;从 研究“常量”发展到研究“变量”,从 研究“有限”发展到研究“无限”,初等数学更多地在“有限”的领域里讨论,更多地以“有限”为手段和工具进行讨论;高等数学则更多地在“无限”的领域里讨论,更多地以“无限”为手段和工具进行讨论。为了让学生快速直观的了解微积分,首先介绍其中蕴含重要思想的数学——无限,下面举两个例子说明之。
显而易见0.9<1,0.99<1,0.999<1,那么问学生,是否有几乎所有的学生都认为于是问学生比1小多少,有的学生回答是,0.000…1,那么该数是一个有限的数,与上面有限与无限数的差,结果不符,教师提出结论,学生聚精会神,但满脸疑惑,这是教师给出证明,方法有多种,略举如下。
看到教师给出的证明,学生既感到趣味盎然,眼神里又充满疑惑,此时,教师引导学生,其实无限和有限存在既对立又统一的关系,我们要用辩证的观点看待世界。
例2 “有无限个座位”的教室。
有限和无限的特点可以从下面的小故事反映出来。

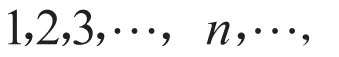

无限的情况:把刚刚的教室和学生人数无限化,设甲班课堂中有学生无穷多个,记为教室中有无穷多个座位,编号为:此时,每人一个座位,很容易安排,令即可。问题是:又有乙班有学生无穷多个,记为,也要到该教室来上课,问能否实现每人对应唯一的座位。引导学生发现方法:即可。教师再抛出问题:该教室坐满后,如果又来了无穷多个班级,且每个班级中都有无穷多个学生,还能否安排,使得每个学生一个座位?此时,学生积极思考,并已经感受到“无限”的神奇魅力,“无穷大”正如此有效地激励着学生的智力。引导学生发现,在无限集合中,“部分可以等于全体”(这是无限的本质),而在有限的情况下,部分总是小于全体。建议学生课后了解“芝诺悖论”“阿基里斯追不上乌龟”等趣味问题,培养兴趣,对比分析。
四、结合专业,互相联系
随着科技和社会的飞速发展,学科间知识的交叉和渗透越来越频繁,高等数学这个工具被越来越多的应用到生产、工作和社会活动中。例如,电气工程的设计与计算、气象站汇集的气压雨量等资料、药物疗效的分析、城市发展规划的决策、工厂产品的生产、成本、费用的优化等都需要建立数学模型来解决问题。可以说高等数学的应用覆盖到物理、化学、生物、医学、经济管理、军事战争等众多不同学科领域以及日常生活中。以广州南洋理工职业学院开设的专业为例,简要论述高等数学在经济学、计算机领域以及日常生活中的应用,阐述数学的实用价值,亦可激发学生学习兴趣,促进数学与专业课的融合,进而使学生意识到学习高等数学的重要性和必要性。
1.数学在经济方面的应用
有效的处理经济和社会合作活动中的效益分配问题,可以用Shapley值方法。经济中各部门之间投入产出的平衡关系,需要用矩阵的理论、代数方程等来更好的解决。微积分在经济分析中占举足轻重的地位,对于一个企业来说,企业要获得更好的发展,就要对经济问题的分析定量化、准确化和精密化。对导数概念的引入,用经济学中的生产成本的边际效应和金融资产价格对利率的敏感性引入,让学生感觉数学“亲近”得多。经济中诸如最低成本、最小费用、最大利润等问题,在数学上可归结为最值问题。经济中的边际成本、边际收益、边际利润、弹性分析,归结为数学中的绝对变化率及相对变化率问题,要用导数的知识来解决。经济总量及变动分析、消费者盈余等问题,也要用微积分的知识。利用极限解决连续复利问题。例:本金A为1元,年利率r为100%,一年计息一次,则一年后的本利和为A(1+r)=2元。若一年分n次计算复利,则每期利率为一年后的本利和为可以看出,一年内,计算利息的次数越多,一年后的本利和越大,但会不会无限增大呢?利用极限的知识,知k年后的本息和[5]。
2.数学在计算机方面的应用
随着人们对大容量数据的存储需求,光盘制品的数据容量大小取决于信道的总长度和信道上存储数据的线密度,如何使信息存储最大化,信道长度的计算,需要建立螺旋线的极坐标下方程,根据极坐标下曲线弧长的微分,写出螺旋线的式子,然后需要用到定积分的知识求解;计算机断层成像(CT)技术的图像重建,需要利用积分变换的公式、代数方程、矩阵的理论、迭代算法等知识来解决等;
3.数学在日常生活中的应用
计算平放的圆柱形油桶里还剩下多少油;求盘山公路的长度,即求光滑曲线弧长问题;湖泊中的含某污染物A的浓度不得超过国家规定指标,计算经过多长时间,湖泊中污染物A的含量降至规定指标内;药品在体内的含量随时间的变化分布与排除问题;用定积分计算交流电路中电阻元件从电源吸收的平均功率;香烟过滤嘴的作用;人口的预测与控制等等,这些问题的解决,要用还可以继续计算,到微分方程等知识。讨论空气污染问题,可以用马氏链模型等。考试中学生作弊现象的调查与估计,亦可建立概率模型分析。这些例子让学生感受到,生活中无处不用数学。
五、注重方法,提升能力
结合学生的认知水平及数学具有的概念的抽象性、推理的严谨性、结论的明确性、应用的广泛性和知识的积累特性等特点,告诉学生学习过程中应注意:准确理解基本概念、正确理解基本定理和公式、掌握基本的计算技能;鼓励学生探索这些基本概念和技巧在其他课程和学术研究中的延伸和应用;掌握好重点与难点;注意每个问题的引例,还应该把握好几个关系:有限与无限的关系、静止与变化的关系、离散与连续的关系。
实践证明,采取以上教学策略的绪论课,受到学生的一致好评,学生了解本课程的历史、基本内容和思想、与专业课的联系等,兴趣盎然、信心满满,对继续学习本课程充满期待和探索的欲望。教师想要使绪论课更丰富、精彩、完善,需要结合学生的特点、专业特征及社会发展的需求,不断的探索与实践,与时俱进,在新时代新使命的社会背景下,探索新方法、新策略、新技巧、新艺术,使高等数学绪论课能更好地为本课程奠定基础。

