考虑地震损伤的RC 框架构件滞回模型研究∗

李英民 周上鉴 刘杰东

(1.重庆大学土木工程学院 400045; 2.山地城镇建设与新技术教育部重点实验室(重庆大学) 400045;3.重庆市聚友建设工程有限公司 400045)

引言

工程结构抗震性能评估的基础和关键在于合理确定结构数值计算模型。遭受地震作用后受到损伤破坏的钢筋混凝土框架结构在经历较强的二次地震作用时,其抗震能力可能迅速降低直至结构破坏[1,2]。同时,地震损伤导致构件的强度、刚度等力学性能发生不同程度的退化,从而使其计算模型相较于新建结构发生较大变化。因此对震损结构进行抗震性能评估的前提在于合理的数值计算模型参数。

迄今国内外对钢筋混凝土框架结构滞回模型研究成果较多,但其中较为成熟的研究及成果大多针对新建结构或未考虑结构的损伤[3-6],近年来关于震损结构滞回模型的研究虽逐渐增多,但仍存在一些尚未解决的问题。欧进萍等[7]在确定地震受损构件恢复力骨架线时,构件受损后屈服位移和屈服力的确定存在一定的多样性。按周小龙[8]方法采用47 组构件试验数据拟合出的关系式,数据样本量偏少,拟合时未考虑轴压比及体积配箍率等常见参数的影响,且未进行滞回模型合理性及必要性验证。李洪泉等[9]提出的钢筋混凝土压弯构件强度损伤模型需先分别测得无损构件和受损构件的动力特性,才能确定损伤指数D值取值,因此该方法在实际工程应用中存在不便。而贾益纲等[10]采用基于三维虚拟层合单元理论的分析方法建立了3 种不同框架柱轴压比的框架模型,并分别取单榀框架进行抗侧性能分析,得出轴压比越大,框架抗侧移刚度退化速率越快。Zhai 等[11]从统计学角度出发研究得出,强震后余震对结构的影响取决于结构周期、延性系数、余震强度等,且对短周期结构强度折减系数的影响比长周期结构强。Yan 等[12]考虑引起损伤的循环加载次数和控制位移影响,提出了量化地震破坏和衰减系数的方法,并将试验骨架曲线简化为三线性模型。郭宗明等[13]在不考虑混凝土拉压损伤影响及纵筋非弹性屈曲效应的前提下,基于刚度退化和纤维单元建立的损伤模型避免了多次引入加权系数导致的损伤指数在转化过程中的不确定性。赵志鹏等[14]通过对比分析国内外典型RC 构件损伤模型,认为Park-Ang 损伤模型更适用于RC 柱。

本文在文献[8]的基础上,基于不同震损状态的钢筋混凝土构件数值计算模型,采用非线性回归分析方法对美国太平洋地震工程研究中心(PEER)提供的钢筋混凝土构件低周反复加载的试验数据进行拟合,得到构造构件损伤程度与剩余强度、刚度等的定量关系,基于适当假定,对震损钢筋混凝土构件的滞回模型进行确定,并对其进行合理必要性验证[15],为震损钢筋混凝土框架结构抗震性能评估提供参考。

1 震损构件滞回参数确定方法

震损钢筋混凝土框架结构中,构件滞回模型的建立包括选择地震损伤模型,确定震损构件滞回骨架线和滞回规则三部分[15]。本文采用Park-Ang 模型[16]作为损伤程度的判据,以修正的Ibarra-Medina-Krawinkler 退化模型[17](以下简称“修正IMK 退化模型”)定义无损构件与震损构件的滞回规则。

1.1 Park-Ang 损伤模型

Park-Ang 损伤模型反映了最大位移响应与累积滞回耗能相互影响,具有广泛的应用基础。表达式如式(1)所示：

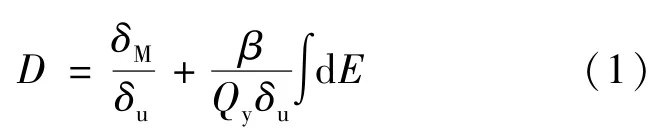
式中：D为构件损伤指数; δM为地震作用下构件最大变形; δu为构件单调加载极限变形; β 为能量项加权系数; Qy为计算屈服强度;∫dE 为累积滞回耗能。β 和δu计算公式分别参考文献[16]和文献[18]。

1.2 震损构件滞回规则

修正IMK 退化模型[17]通过循环退化指数βi反映震后结构构件的性能退化,震损构件的滞回规则通过对退化模型中反映滞回规则的相应参数进行折减来反映[15]。

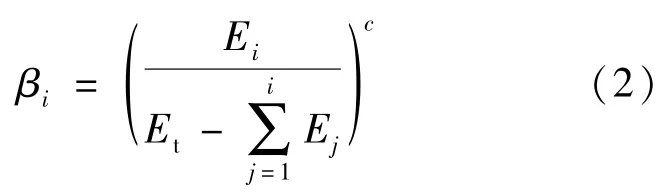
式中：c为衰减率指数; Ei为第i 个滞回半圈的滞回耗能;∑Ej为累积滞回耗能;Et为构件滞回耗能能力,按式(3)计算：

式中：Fy为构件的屈服力;δy为构件屈服位移,计算公式参考文献[19];λ为滞回耗能参数,计算公式参考文献[20],如下：

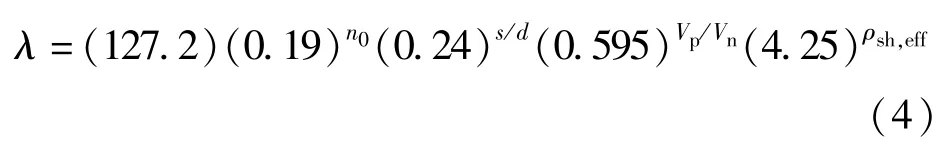
式中：n0为构件轴压比;s为构件箍筋间距; d为截面有效高度; Vp为对应屈服弯矩的剪力值;Vn为构件抗剪强度; ρsh,eff为有效配箍率。

由式(2)和式(3)可知,构件受损后,βi的计算需求得震损构件滞回耗能能力Etd=λdFydδyd,因此,钢筋混凝土构件震后滞回规则的定义实质在于震损构件滞回耗能参数λd的确定,定义滞回耗能参数退化系数αλ计算公式为：

1.3 震损构件滞回骨架线的确定

1.强度退化系数

强度退化系数反映了构件损伤后的强度退化幅度,其退化规律如式(6)所示[17]：

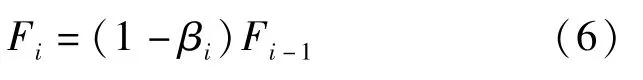
式中：Fi和Fi-1分别表示第i个滞回半圈加载后构件的同向屈服强度。损伤指数为D时,强度退化系数αF计算公式如下：

式中：Fyd为构件损伤指数为D时的屈服强度。2.刚度退化系数

刚度退化系数反映了构件损伤后刚度退化幅度,即：

式中：k0为构件初始刚度;为构件受损后刚度,确定Fyd后,通过几何关系求得具体数值。

3.震损构件滞回骨架线的确定

确定震损构件退化系数αF和αK后,即可得震损构件滞回骨架线如图1 所示,确定方法如下[15]：

(1)无损构件骨架线的确定。参考文献[19]中的经验公式给出关键点参数;

(2)震损构件骨架线弹性上升段的确定。确定构件D及βi,计算其对应的αF和αK,震损构件骨架线弹性上升段由图中几何关系确定;

(3)震损构件骨架线屈服后上升段的确定。加载过程中刚度退化规律近似于强度退化规律[17]：/k1=Fyd/Fy,同时假定损伤构件的极限位移近似取为未损伤构件的相应值：xud=xu[7];

(4)震损构件的骨架线下降段的确定。相关研究表明[7,17]损伤构件屈服后下降段刚度与无损时基本一致： 取=k2。

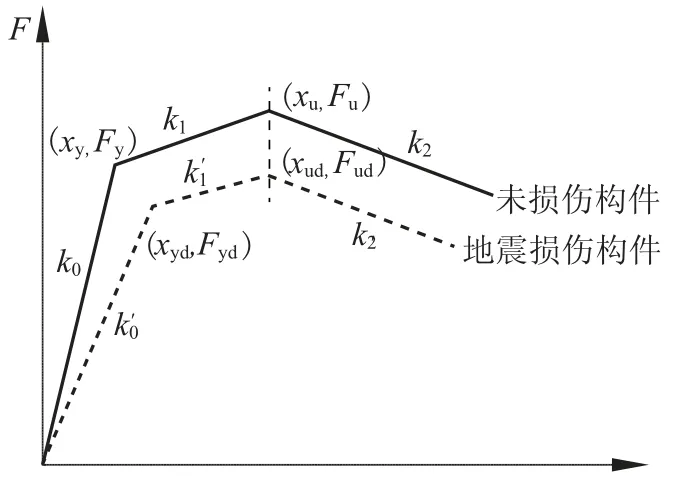
图1 震损构件恢复力骨架线Fig.1 Hysteretic bone curve of seismic damaged members

1.4 震损构件试验数据的选取和处理

建立震损结构滞回模型,需对大量构件的试验结果进行综合分析。本文所采用的构件低周往复加载试验值均取自PEER 试验数据库,样本数为97,选取原则为：矩形构件且抗震构造良好,试验轴力保持恒定或轴力为零,破坏形式为弯曲破坏。97个试件的截面高度、轴压比、剪跨比等8个参数的平均值、标准差和变异系数见表1。基于工程设计中常用试件参数范围进行取值,所选试件具有典型代表性。

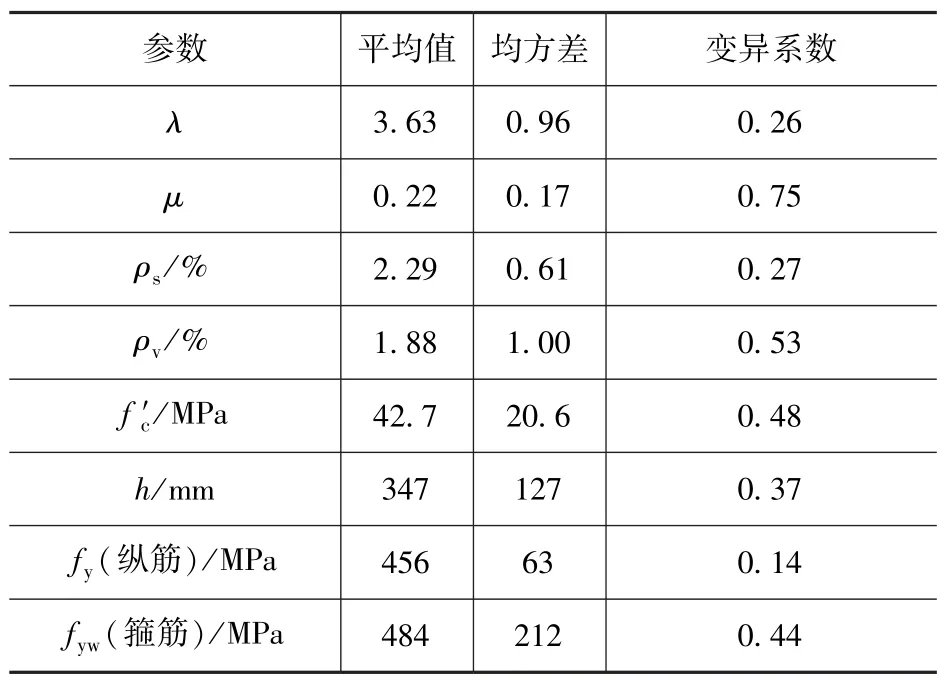
表1 试件参数统计结果Tab.1 Statistical results of specimen parameters

2 震损构件滞回模型中参数的拟合

本文拟采用MATLAB 软件编制相关程序,计算得到97 组不同损伤状态下的αF、αK、αλ,通过回归分析,拟合损伤指数与各退化系数之间的关系表达式。

2.1 强度退化模型

97 组构件强度退化系数和损伤指数对应关系如图2 所示。参照整体数据和单独一组数据的变化规律均能看出,强度退化系数随损伤指数增大而减小,退化速率先慢后快,呈抛物线变化趋势,考虑到需满足边界条件D=0 时αF=1,经一元非线性回归分析,得到αF与D拟合关系如下：

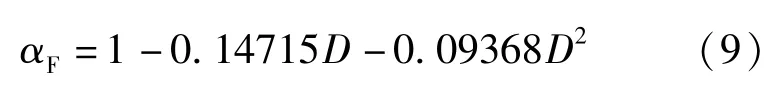
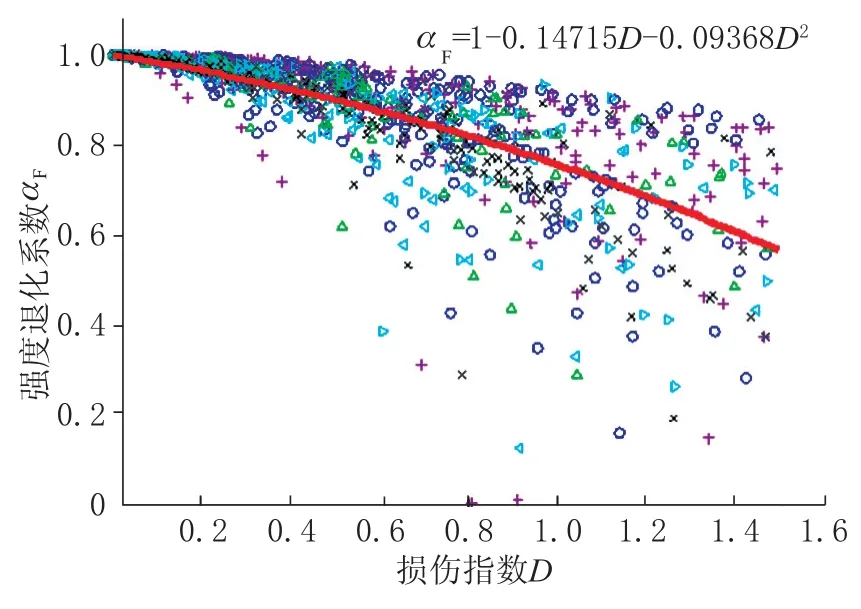
图2 损伤指数与强度退化系数的拟合关系Fig.2 The fitting relationship between the damage index and the degradation coefficient of strength

由式(9)计算得到,当0≤D＜0.4 时,强度退化最大接近10%,式(9)能较为精准地估计强度退化系数。而当0.4 ≤D＜1 时,对应Park等[16]提出的损伤等级,构件处于严重破坏阶段,数据预测的准确性随D值增大而减小,当构件破坏程度较严重时,由于剩余强度数据离散性较大,此时式(9)适用性较低。

综合分析导致数据呈发散状的原因有： (1)式(9)考虑自变量较单一,试件中其他参数如轴压比、剪跨比等差异性的影响则未考虑; (2)以Park-Ang 震损模型为破坏准则,损伤指数D≠1时,部分试件也可能发生破坏; (3)混凝土材料本身离散型较大及试验客观环境不同。因此考虑1.4 节中提到的试件截面高度、轴压比等8 个基本参数的影响,对式(9)进行改进。由图2 中强度退化系数随损伤指数的非线性退化规律,假定改进后的拟合关系式仍为二次抛物线形,设改进后的拟合关系式为：

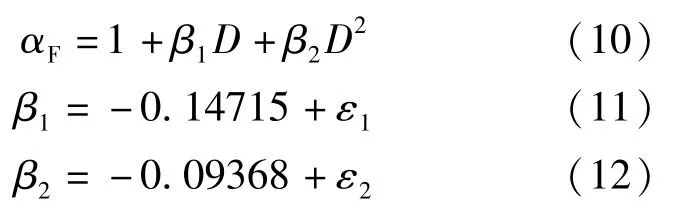
式中：β1、β2为修正后的回归方程系数;ε1、ε2为考虑设计参数影响的修正系数。

将97 组数据按式(10)进行回归分析,得到对应β1、β2、ε1、ε2值。以轴压比、剪跨比等8个参数为自变量,ε1、ε2为因变量,将各数据转化为符合线性回归模型的相应数据并以SPSS 统计分析软件进行回归分析,筛选出有显著影响的因素,得到ε1、ε2经验公式如下：

式中：fyw为箍筋屈服强度;为混凝土抗压强度;n0为试件轴压比;ρs为纵筋配筋率。

由式(13)、式(14)可知,对强度退化模型影响较大的参数为试件轴压比、箍筋屈服强度,其次是纵筋配筋率及混凝土强度。因此,改进后的回归方程系数拟合式为：

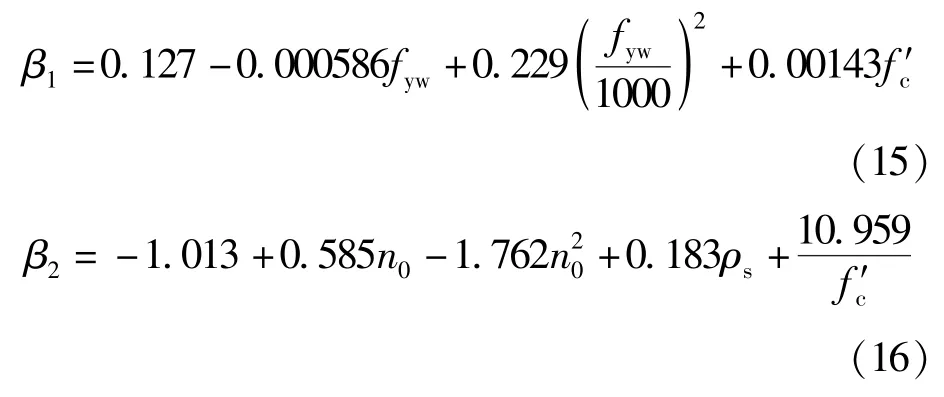
图3 为其中某单根构件随加载历程的不同滞回环数对应的强度退化规律与改进前后拟合曲线的对比情况,可直观地看出改进后的拟合关系式较好地提高了预测准确度。

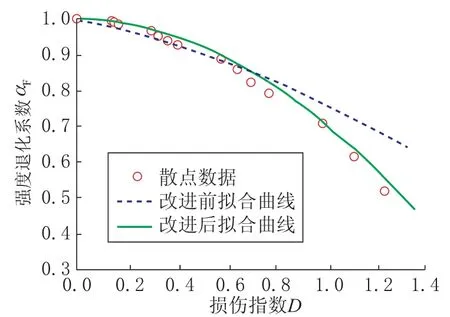
图3 改进前后的拟合关系对比Fig.3 Comparison of fitting relations before and after improvement

2.2 刚度退化模型

同样通过该拟合过程,计算出各构件刚度退化系数和损伤指数对应关系如图4 所示,建立D与αK的拟合关系式为：

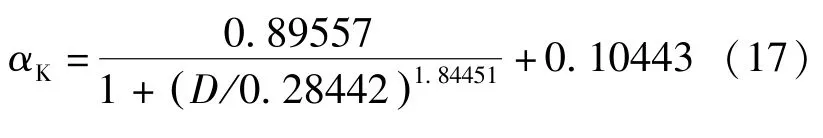
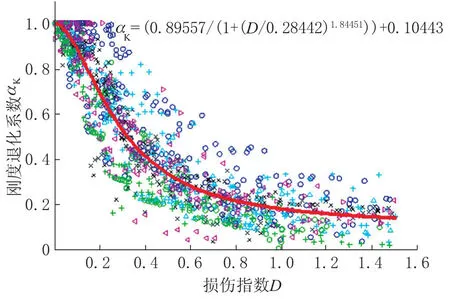
图4 损伤指数与构件刚度退化系数的拟合关系Fig.4 Fitting relation between damage index and stiffness degradation coefficient of components

当D=0 时αK=1,此时式(17)满足边界条件,且由图4 可得到式(17)能反映刚度退化随损伤程度增大的变化规律。此外,R2=0.9,表明式(17)与数据吻合度较好,能较准确地预测构件刚度退化系数。拟合曲线两侧的数据分布均匀且大多集中在曲线附近,离散型小,不需进一步改进拟合关系式。

2.3 滞回耗能退化模型

97组不同损伤状态下对应的滞回耗能参数退化系数如图5 所示,建立D与αλ的拟合关系：

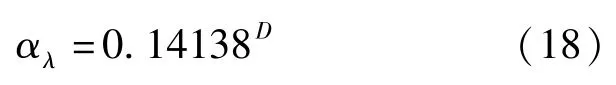
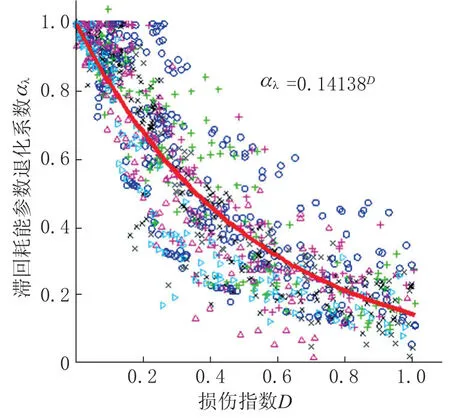
图5 损伤指数与构件滞回耗能参数退化系数的拟合关系Fig.5 Fitting relation between damage index and degradation coefficient of hysteretic energy parameters of components

当D=0 时αK=1,拟合公式满足边界条件,R2≈0.9,拟合结果较好,且拟合关系曲线两侧数据分布均匀,离散性小,说明在震损构件损伤指数确定时,根据式(18)能够得到较为准确的滞回耗能参数退化系数,为确定震损构件滞回模型提供数据参考。

采用拟合式(10)、式(17)、式(18)计算得到的Park-Ang 各损伤状态界限点的参数退化系数值如表2 所示。

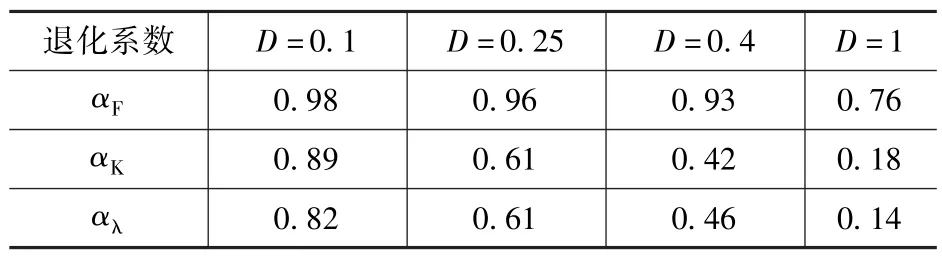
表2 Park-Ang 各损伤界限点的参数退化系数值Tab.2 Parameter degradation coefficient values of damage states boundary points

3 震损钢筋混凝土框架结构滞回模型合理性验证

本节分别采用直接分析和间接分析两种流程对震损结构进行弹塑性时程分析,对比验证震损结构滞回模型的合理性。直接分析将首尾相连的两次或多次地震动一次性输入到无损结构; 间接分析中的初始分析模型取首次地震动输入后获得的震损结构,震损构件滞回模型由2.3 节方法得出,随后再次输入地震动对结构进行弹塑性时程分析[15]。分析流程如图6 所示。

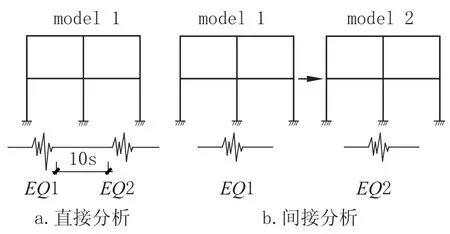
图6 合理性验证分析流程Fig.6 Flow chart of testing rationality

以二层钢筋混凝土框架结构为例。模型环境为8 度区,II类场地,地震分组为第二组,丙类结构。材料强度等级：纵筋HRB400,箍筋HRB300,混凝土C35。楼面荷载标准值： 恒载为5kN/m2,活载为2kN/m2,取一榀框架计算,构件截面尺寸与配筋情况如图7 所示。

利用OpenSees 软件,采用修正IMK 退化模型通过定义塑性铰的弯矩-转角滞回曲线识别震损构件,并分别计算相应震损构件的损伤指数与滞回模型参数,建立震损结构计算模型。对无损结构输入PGA为0.3g的El-Centro 地震记录,以结构最大层间位移角为控制指标,得到轻微或中等破坏的震损结构,并对其输入0.4g的El-Centro波。

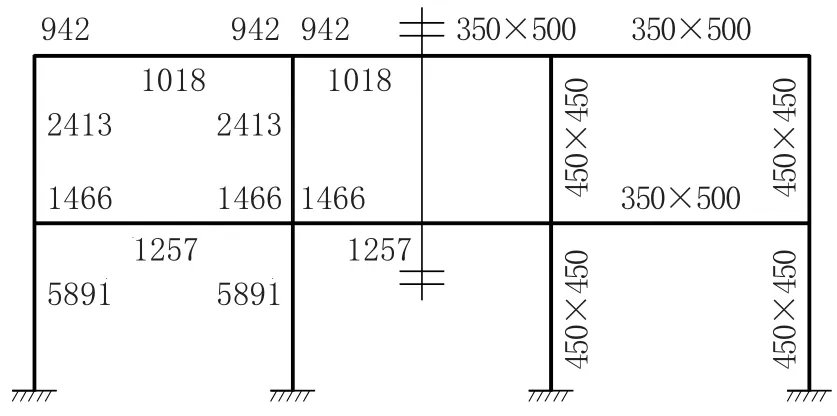
图7 构件截面信息(单位： mm,mm2)Fig.7 Component section information(unit： mm,mm2)

按本节提出的合理性验证方法对本算例中二层框架结构分别按直接分析、间接分析两种方法进行弹塑性时程分析,图8给出了两种分析方法在二次地震输入后结构层间位移角时程对比曲线。

图8 两种不同方法层间位移角时程对比曲线Fig.8 Comparison between time-history curves of story drift angle in two different ways

由图8 可知,两种方法得到的时程曲线基本吻合,变化趋势保持一致,证明本文提出的滞回模型是合理的。

4 震损RC框架结构滞回模型考虑地震损伤的必要性验证

以对新建结构输入地震波得到的震损结构为基础,建立按本文方法考虑地震损伤的震损模型和不考虑损伤的完好模型。通过再次输入相同地震波,对两种计算模型分别进行动力弹塑性分析,得到考虑地震损伤后对计算结果的影响大小,以此验证采用震损构件滞回模型的必要性,验证流程如图9 所示。

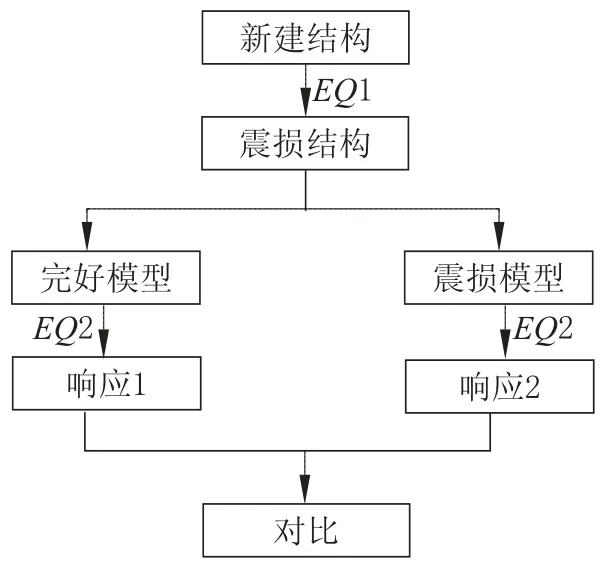
图9 必要性验证流程Fig.9 Flow chart of testing necessity

对本算例中二层框架进行间接分析,图10给出了是否考虑震损影响的两种工况下,结构最大层间位移角的对比情况。

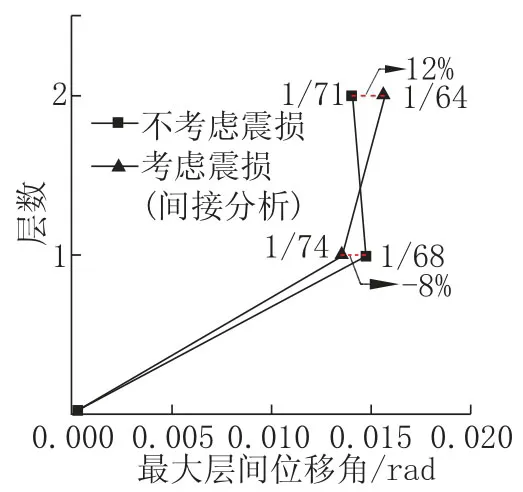
图10 两种不同工况最大层间位移角比较Fig.10 Comparison between maximum story drift angle in two different condition

将考虑震损影响与否的层间位移角最大值之差与不考虑震损时层间位移角的比值定义为位移增大率。由图10 可知,考虑震损情况后,震损结构底层层间位移角减小了8%,二层最大层间位移角增大12%,表明在经历第二次地震作用时,结构薄弱层由一层变为二层,结构力学性能的退化将影响其地震响应,在设计时亦不容忽视。分析可知,是否考虑地震损伤对结构分析结果影响较大,对震损结构进行动力弹塑性分析时应采用考虑地震损伤影响的滞回模型,从而模拟结构力学性能参数的折减。

5 结论

1.提出了震损构件滞回模型中参数的确定方法和建立滞回模型的基本思路,并给出滞回模型合理性和必要性的验证方法。

2.考虑轴压比、剪跨比、配筋率等因素影响下,得到了构件损伤指数与强度、刚度、滞回耗能参数退化系数对应的拟合关系式,提高了剩余强度预测准确度。

3.通过具体算例证明退化模型的合理性和必要性。地震损伤对钢筋混凝土框架结构的力学性能退化的影响不容忽视,在对震损结构进行动力弹塑性分析时应采用考虑地震损伤的滞回模型。