桥式起重机轨迹规划及其跟踪方法研究

李 瑶，邵雪卷，张学良

(1. 太原科技大学电子信息工程学院，太原 030024；2. 太原科技大学机械工程学院，太原 030024)

桥式起重机作为一种大型的工程搬运设备，在重工业、国防和国民经济中发挥着举足轻重的作用。但起重机是一个非线性、强耦合的欠驱动系统，小车的加速、减速、以及匀速行驶过程中负载摆角都会影响起重机的运行。人们无法直接对起重机负载进行控制，只能通过控制小车的运动，并在不影响其定位的前提下，间接地抑制负载摆动。因此，负载在水平运行过程的定位与防摆控制效果直接影响起重机的工作效率[1]。

针对起重机定位与防摆的控制研究，文献中大多数方法是调节控制，比如部分反馈线性化[2]、滑模控制[3]、模型预测控制[4]、模糊控制[5-7]、基于能量的控制方法[8-11]或几种控制方法的结合等。大量的实际操作表明，设计合理的参考轨迹也可以让小车进行精准定位和减小负载摆动。文献[12]基于相平面的几何分析法，将台车运动引起的负载摆动映射到相平面中，构造出一条具有解析表达式的三段式加速度消摆轨迹。文献[13]中，给出S型参考轨迹后，根据加速度与角度之间的动态耦合关系，设计了一个消摆环节，达到了定位消摆的目的。此外，轨迹规划与轨迹跟踪的结合使用也得到一些学者的关注。该方法的核心思想是规划一条平滑的参考轨迹引导小车运行，然后设计相应的跟踪控制器, 这样不仅会使小车运动更加平稳, 还能更好地考虑一些物理约束条件(如小车最大速度、加速度，最大摆角等)。文献[14]对小车加速度进行整形，给出了一条能够消除负载摆动的加速度参考轨迹，并运用滑模控制跟踪该轨迹。文献[15]中给出S型参考轨迹后设计自适应控制器对其进行跟踪，该方法的轨迹不仅能使小车能准确定位，也能减小负载摆角。文献[16]通过对吊车动力学模型进行一系列的变换, 采用S型参考轨迹后，设计了一种新颖的跟踪控制器,在精准定位和减小负载摆角的同时能够保证小车的平滑启动与运行。

内模控制因跟踪调节性能好、鲁棒性强以及易于设计实现等特点得到了广泛应用[17]。本文提出了一种基于内模跟踪控制的策略，跟踪的轨迹是在考虑起重机本身约束条件后，给出的一条加速度参考轨迹，该加速度轨迹能够使负载消除残摆，再通过内模控制器对系统进行跟踪控制，不仅使小车能快速精准地达到目标位置，而且当小车带动不同负载运行时，摆角依旧在约束的范围内。

1 问题描述

主要针对2-D桥式起重机系统，对小车水平运行过程(缆绳长度不变)进行研究。其模型图如图1所示：

图1 2-D桥式起重机模型
Fig.1 2-D overhead crane model

系统的运动学模型为：

(2)

模型中M和m分别代表小车和负载的质量，l为缆绳长度，x(t)为小车位置，θ(t)为负载摆角，u为驱动力，g为重力加速度，f为阻尼系数。式(2)化简后可得：

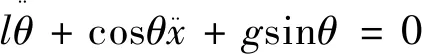
(3)

起重机负载摆角在很小的范围内满足近似关系sinθ≈θ,cosθ≈1.因此，式(3)可重写为：

(4)

在平衡点θ=0附近，由近似关系，式(1)和式(2)可化简为：

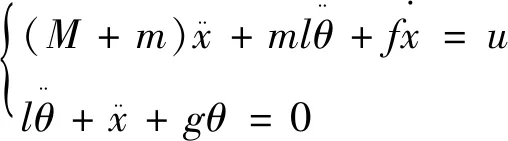
(5)

式(5)做拉氏变换得到系统的传递函数为：

(6)

由式(3)可以看出，小车加速度和负载摆角之间存在着动态耦合关系，小车加速度直接影响负载的摆动。因此，合理地规划轨迹可以使小车加速运行时减小负载摆角，在小车匀速行驶及静止时不存在残摆。

2 加速度轨迹规划

在进行轨迹规划时，需要考虑实际起重机小车运行时的一些约束条件：

(1)小车能在有限的时间内且无超调的收敛至所设定的距离点pd，即x(t)→pd.

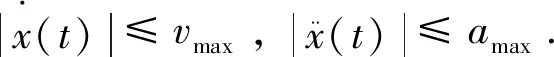
(3)最大负载摆角应保持在可接受的角度范围内，即|θ(t)|≤θmax.

(4)当小车以恒定速度运行及到达目标位置时，负载摆角应为零。

参考轨迹的给定能满足的约束条件是：

(7)

小车水平运行时，负载摆角变化如图2所示：

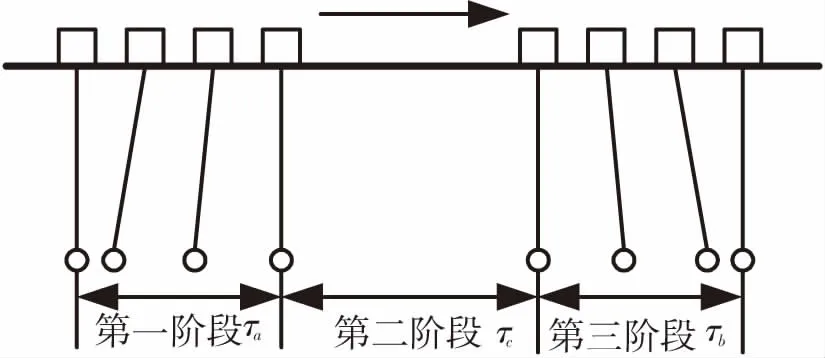
图2 水平运动示意图
Fig.2 Schematic diagram of horizontal motion

该过程可分为三个阶段，第一阶段τa：加速运行。此时摆角大小由零随速度的增大反方向增大。第二阶段τc：匀速运行。当速度达到最大值后开始匀速运行，这个阶段的负载摆角应为零。第三阶段τb：减速运行。运行时间与第一阶段的运行时间相同，该阶段的负载摆角存在，当速度减为零时，摆角也变为零。通过分析小车运行过程，给出加速度参考轨迹，本节将对参考轨迹进行详细描述。

当小车以恒定加速度运行时，解式(4)可得：

(8)

通过上述分析，加速度参考轨迹如图3所示：

图3 加速度及速度参考轨迹
Fig.3 Acceleration and velocity reference trajectory

τa与τb阶段是一个对称的运动过程，因此，只需研究τa过程。该阶段的加速度可以是由几段恒定的加速过程组成，如图4所示：

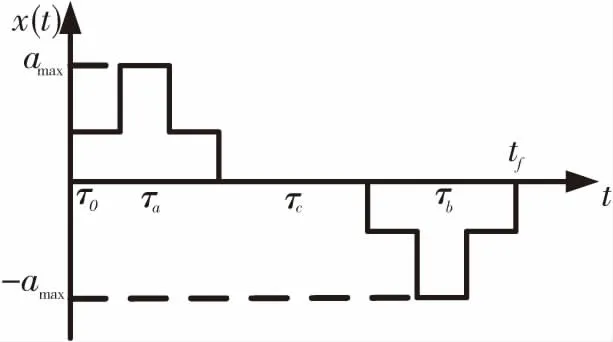
图4 加速度参考轨迹
Fig.4 Acceleration reference trajectories

给出τa阶段加速度轨迹的一般形式：

(9)

其中ai为常数，τi是以加速度为ai运行时的加速时间，阶跃函数定义为：

(10)

将式(9)带入式(8)中，可得：

(11)

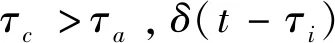
(12)

负载残摆为零时θ(t)=0，式(12)可写为：

(13)

整个加速完成后速度达到最大值，最大速度是：

(14)

由给定约束条件和式(13)、式(14)可确定各阶段的加速时间以及相应的加速度。

当N=1时，τa阶段以一个恒定的加速度进行加速运行，如图3所示。有三个未知参数即该阶段的加速度和加速时间需要确定，有

(15)

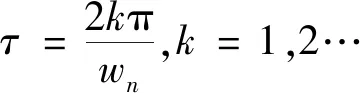
(16)

最大摆角θmax(t=τ/2)=-2a0/g.

给定pd为4 m，最大速度0.5 m/s，缆绳长度l=1.2 m，重力加速度g=9.8 m/s2.计算可得τa时段的各加速度以及对应的加速时间，其结果为：

当N=3时，加速度轨迹图形如图4所示，有:

(17)

当τ0+τ1+τ2+τ3=τa=3T时，残摆为零，满足上式，且小车在该时间段加速运行时，加速度增大再到减小为零是一个对称的过程，因此可知τ0到τ1和τ2到τ3时间段是相同的，因此，可解得：

τ0=0,τ1=0.5T,τ2=T,τ3=1.5T，最大摆角为：

(18)

计算得到N=3时各参数：

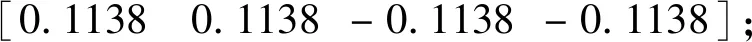
[0 1.0988 2.1975 3.2963]；

τc=4.703s；θmax=1.333°.

当N≥5时，除了式(12)、式(13)外，还需额外构造方程，但是在同样能满足消除残摆的情况下，类似这种阶梯型参考轨迹的台阶数越多，计算量也就越大，因此，本文选取当N=3时的加速度参考轨迹。

3 内模控制器的设计

带输入干扰的内模控制结构框图如图5所示：

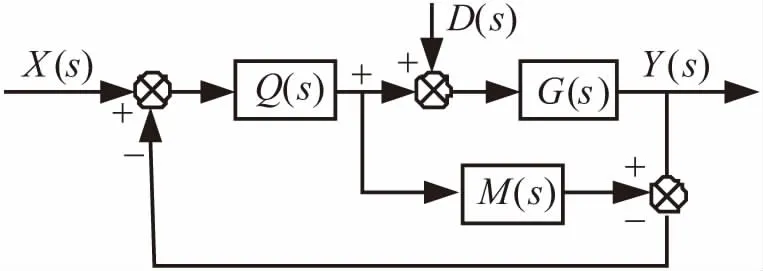
图5 内模控制结构框图
Fig.5 Block diagram of IMC

其中，X(s)和Y(s)分别代表系统的输入与输出，Q(s)为内模控制器，G(s)为被控对象，M(s)为对象的数学模型，D(s)为系统的输入干扰。

在起重机系统中，由式(6)可看出位移与摆角之间的关系如图6所示：

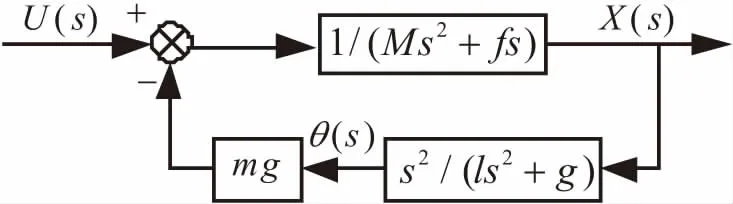
图6 位移与摆角关系
Fig.6 Relationship between displacement and swing angle

通过图6可知，只要给定输入，摆角的变化可由位移得到，因此只需设计定位跟踪控制器。为了设计控制器的简便，对式(6)中的第一个传递函数进行降阶处理，采用Matlab中提供的最优降阶函数opt_app( )进行降阶，降阶后模型的位移传递函数为：

(19)

根据内模控制器的设计方法，内模控制器为：

(20)

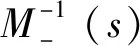
(21)

其中λ为滤波参数，图5可等效化简为图7：

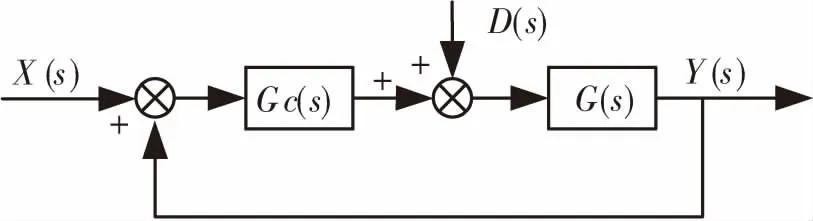
图7 等效内模控制器
Fig.7 Equivalent internal model controller

图7中GC(s)与Q(s)的关系为：

(22)

由分析可知，控制器中只有一个可调参数λ，且λ的大小影响着系统的动态性能。当λ取的值较小时，系统有良好的动态性能，但鲁棒性较差，当λ取值较大时，系统的鲁棒性得到改善，但动态性能有所下降。因此，要选取适当的λ值，使系统达到期望的性能。

4 仿真与分析

为了体现本文参考轨迹的适用性及控制器的可行性，在Matlab中进行仿真。设定小车的距离pd为4 m，阻尼系数f为0.2，最大速度为0.5 m/s，小车质量为5 kg，负载质量为10 kg，缆绳长度为1.2 m，重力加速度9.8 m/s2，则负载摆动的自然频率ωn为2.859 2 rad/s，周期T为2.197 5 s.通过Matlab中降阶函数得到降阶后位移传递函数中的参数K=5,T=75，扰动为d(t)=0.5(t-12).小车以最大速度匀速行驶的时间τc=4.703 s，到达目标位置需要的总时间为tf=11.296 s，最大负载摆角θmax=1.333°，控制器为：

(23)

λ的取值会影响系统的性能，在系统稳定后的第12 s加入输入扰动，小车的位置以及负载摆角结果如图8所示：

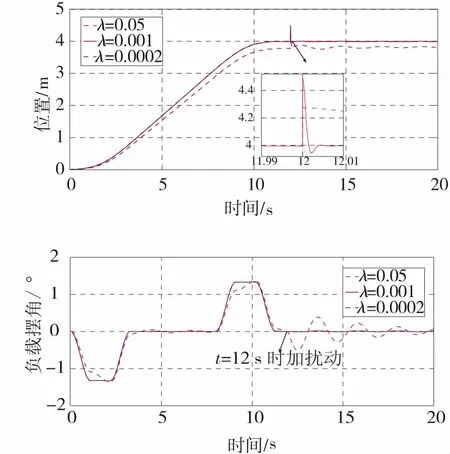
图8 小车位置与负载摆角
Fig.8 Trolley position and load swing angle

当λ=0.001时和λ=0.000 2时，小车位置与负载摆角的响应基本一致，只是在加入输入扰动后，滤波参数小的系统恢复稳定所用的时间短，二者相差时间在0.01s内。当λ=0.05时，小车在规划的时间内不能到达目标位置，且加入扰动后，小车出现了轻微振荡，负载出现了摆动。在仿真的过程中，考虑λ越大，对系统快速性影响较大，因此，在本文中，取滤波参数λ=0.001.

下面具体分析λ=0.001时的小车轨迹跟踪以及负载摆角的情况，并与文献[14]中滑模控制方法进行对比，仿真结果如图9所示：

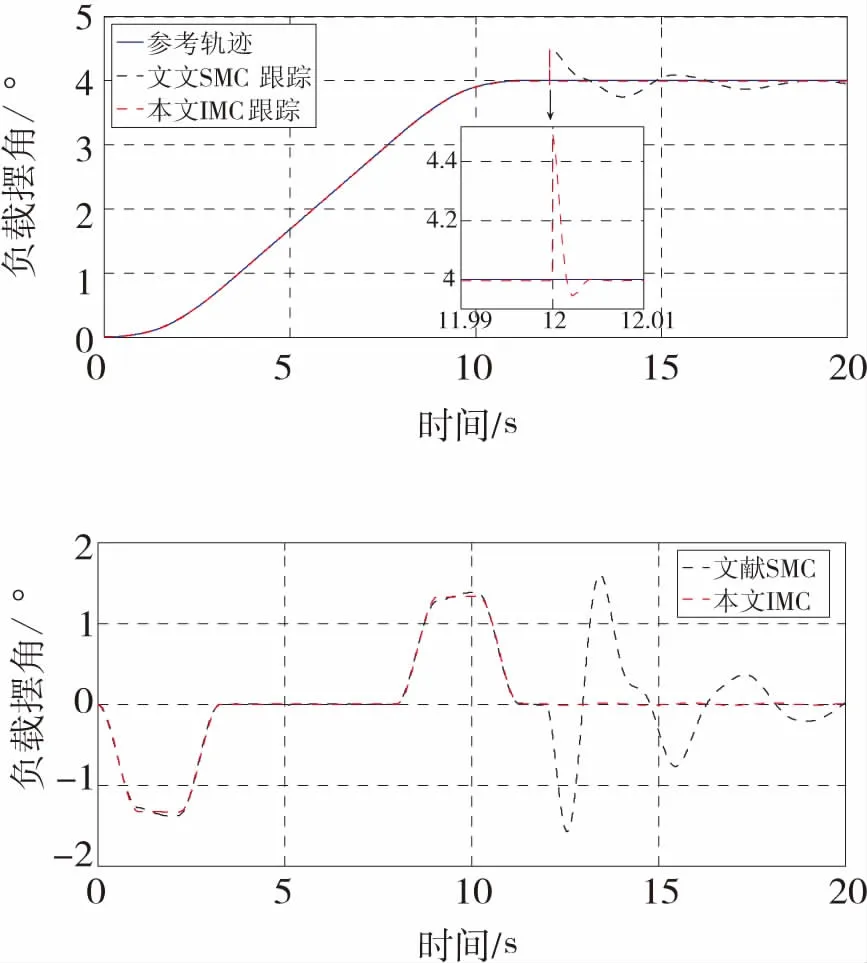
图9 跟踪轨迹及其负载摆角
Fig.9 Trajectory tracking and its load swing angle

从图中可以看出，采用内模控制器和文献[14]中的滑模控制器都能使小车在11.3 s内准确到达目标位置，且定位误差保持在4 mm以内；在12 s加入扰动后，本文方法能使小车在0.2 s内恢复在目标位置，采用滑模控制小车需要轻微振荡后才能稳定在目标位置。本文方法进行跟踪时最大负载摆角θmax为1.33°，与理论计算的结果一致。在加入扰动后的负载会有轻微的残摆，但误差在0.01°内，而文献所用的方法使负载存在较大的残摆，且最大负载残摆为1.1°.通过对比本文和文献仿真结果得出：采用两种控制器都能使小车跟踪上参考轨迹，但是在加入扰动后，本文采用的内模控制可以使系统具有较好的抗干扰性能。

图10 不同负载下的摆角情况
Fig.10 The swing angle under different load

由于改变负载质量不会影响小车定位，图10给出改变负载质量情况下本文及文献[14]负载摆角的仿真曲线。

由图10(a)、(b)和(c)可以看出小车在不同负载下的运行情况，由图可知，采用本文的控制方法不会因负载质量的改变而出现振荡或者大幅摆动，在负载为5 kg时，文献[14]的结果与本文基本一致；负载为10 kg时，出现轻微振荡；而当负载为20 g时，出现明显的大幅度摆动。说明了本文用内模控制能使系统具有良好的鲁棒性。

5 结束语

为了使起重机小车能够快速而准确的跟踪上规划的轨迹，并且在运行过程中减小摆角。本文给出了类似阶梯状加速度轨迹并设计了内模控制器进行轨迹跟踪。结果表明该加速度轨迹易于跟踪且能减小负载摆角；在有内模控制器的情况下，加入输入扰动后系统能快速恢复稳定，并且改变负载质量不会使其摆角振荡。说明采用类似阶梯状加速度轨迹及使用内模控制器能使系统具有良好的抗干扰性及鲁棒性。