台风环境中典型海上风机结构的动力响应数值分析

李 琪1 ， 周文杰， 童建国1， 国 振

(1. 浙江省电力设计院有限公司， 浙江 杭州 310012； 2. 浙江大学 建筑工程学院， 浙江 杭州，310058)

0 引 言

在传统能源日渐枯竭的今天，世界各国加快了新能源的探索与开发，诸如风能、核能、太阳能、潮汐能等，其中风能具有永不枯竭、无污染、直接发电等诸多优点。与陆地风力发电相比：海上风力发电位置更靠近中国能源消耗巨大的东南沿海地区，可显著减少西电东送的相关费用和电能线路消耗；海上风速更大，湍流强度更小，风资源质量高；远离海岸10 km，不占用宝贵的土地资源，也不会带来噪声、视觉的干扰。因此，大力发展海上风电是中国经济新常态下实现绿色可持续发展的重要选择。

然而，中国东南沿海地区台风频发，海南、广东、广西、浙江、福建等地均是主要的热带气旋登陆地区。据中国气象部门统计[1]，中国东南沿海每年登陆的台风及超强台风的数量平均为9个。虽然台风期间可以获得相当可观的发电量，但是极端的环境风场条件也给该区域的海上风电开发与建设带来严重威胁。

单桩基础是目前应用最为广泛的近海风机基础形式，随着海上风电建设向深水区发展，导管架基础也逐渐应用开来，但两者的动力性能差异尚缺少较为细致的研究。本文对比分析台风极端工况下单桩、导管架两种典型近海风机结构的动力响应差异，借助多物理场分析软件COMSOL Multiphysics， 对风机整体结构进行三维有限元建模并考虑极端台风工况下的风、浪、流荷载条件。

1 有限元模型建立

如图1所示，构建的单桩和导管架基础海上风机数值模型为三维有限元模型，均采用欧拉梁单元模拟。风机的机舱和转子等上部结构简化成集中质量点施加在轮毂位置。海床面以下的桩-土相互作用通过非线性弹簧描述，而风、浪、流荷载则直接施加在风机模型的塔架单元上。

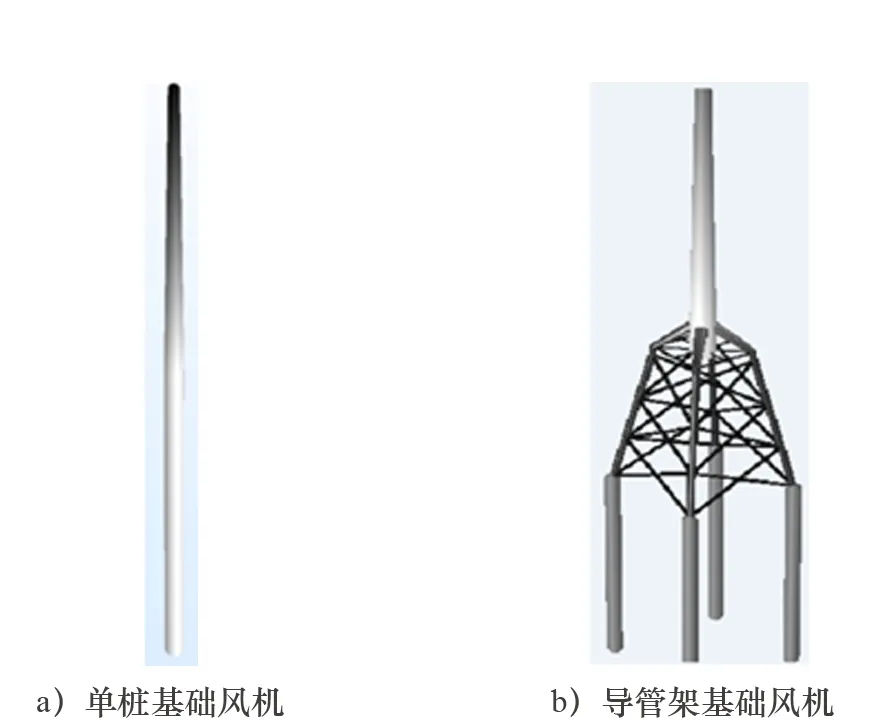
图1 海上风机模型典型结构

1.1 桩-土相互作用分析

模型针对福建近海某处海上风场工程，其海床地基的基本情况如表1所示。计算时考虑海洋环境中的冲刷作用，根据DNV规范[2]，冲刷深度设定为2D(D为桩径)。

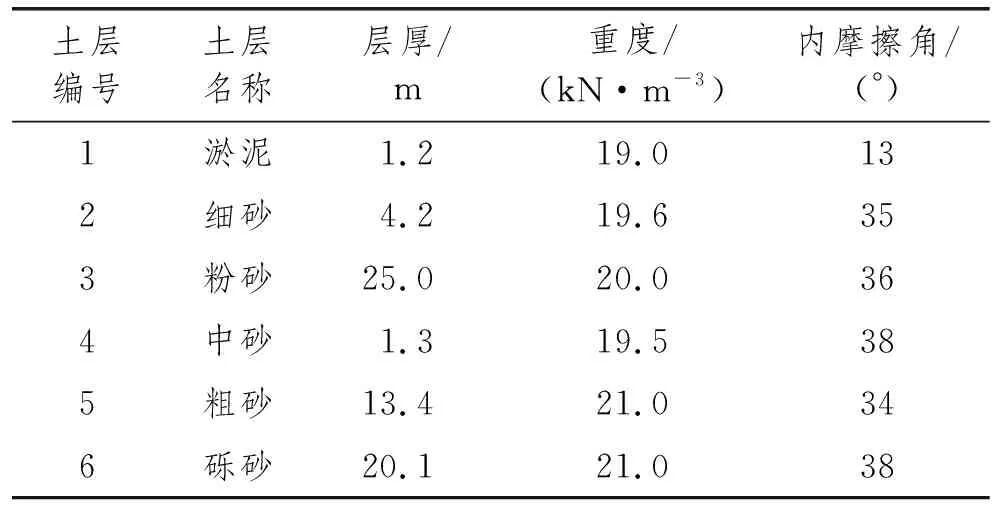
表1 工程地质条件

采用API规范[3]推荐的方法，考虑水平方向、竖向桩侧壁及桩端与土的相互作用，即p-y，t-z，q-z曲线方法。其中，砂土中桩在静荷载、循环荷载作用下的p-y曲线为

(1)

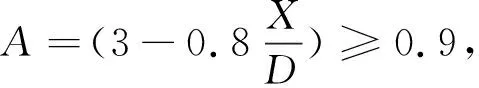
1.2 阻尼参数确定

海上风机结构的阻尼是影响结构动力计算结果精度的重要因素。模型主要考虑气动力阻尼、水动力阻尼、材料阻尼和辐射阻尼。其中，空气动力阻尼与风速大小有关，KÜHN 等[4]研究表明，在风速不太大时，空气动力阻尼比可取为3.5%。水与结构之间产生拖曳力，阻尼比取0.15%。钢材的材料阻尼比一般在0.2%～0.3%，中国相关规范[5]中钢结构阻尼比取值为2%～4%；土体材料阻尼对整体结构的阻尼贡献最大，且随着荷载循环次数的增加不断增大[6]，此处选取8%作为桩、土的材料阻尼。辐射阻尼取值为0.22%。在本数值模型中阻尼比总计为11.87%，各部分具体设定如表2所示。

表2 阻尼明细表 %

1.3 荷载分析与计算方法

1.3.1 风荷载分析计算

选用的台风风谱为石沅台风谱，该谱是水平方向台风风速谱，由石沅等[7]根据上海地区的台风统计资料拟合得到。该风谱不随高度改变而改变，是一个经验性台风谱，基本形式如下：

(2)

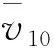
利用MATLAB编制程序对风机轮毂点进行单点脉动风速的时程模拟。为了检验模拟效果，将模拟的风速时程数据进行脉动风功率谱估计。对比可见模拟谱和原始谱具有较高的重复度，效果较好，如图2所示。模拟得到的脉动风速时程数据为风荷载计算和结构动力分析提供输入。

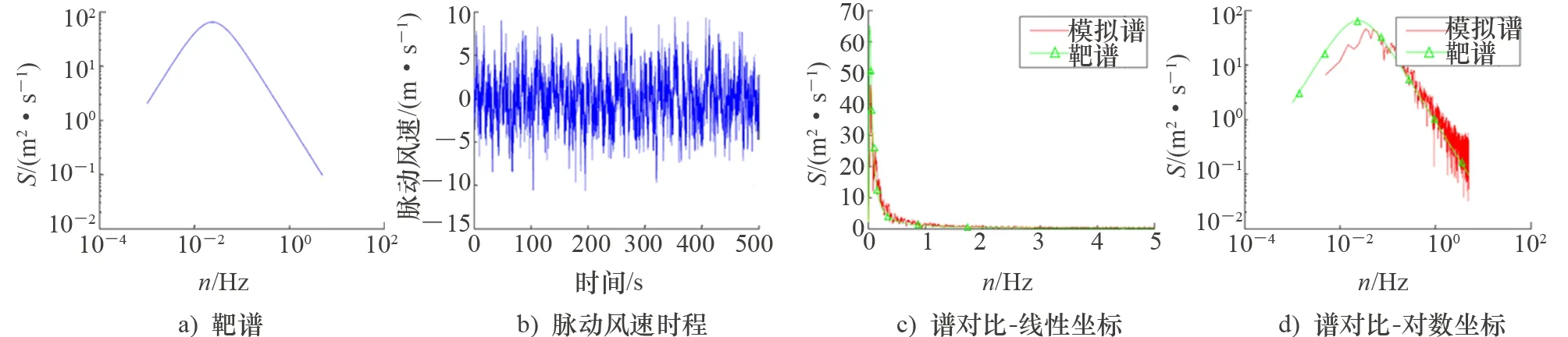
图2 基于石沅谱单点脉动风速时程模拟结果

在台风工况下，为减小风荷载，风机常处于停机状态，叶轮顺桨制动，因此计算常态工况下风轮风推力的推理系数法已不再适用。本文采用经典的叶素-动量理论[8]计算台风下叶轮风荷载。以NREL 5 MW海上风机的叶片翼型参数为例计算台风下风轮荷载，不考虑各叶素间扭角的不同。

1.3.2 波浪荷载分析计算

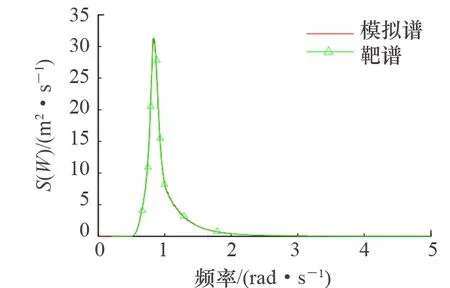
图3 波浪模拟谱与靶谱对比

基于JONSWAP谱对随机波浪进行时程模拟，采用等分频率法对波浪进行线性叠加模拟。利用MATLAB软件对随机波浪进行时程模拟。模拟谱与靶谱对比结果如图3所示。

波浪对小尺度构件的波浪作用力主要是黏滞效应引起的拖曳力和质量效应引起的惯性力，计算方法采用1950年提出的Morison方程[9]。波浪力作用于单位长度直立固定桩柱体的作用力为

(3)

式中：fD为拖曳力；fI为惯性力；CD为拖曳力因数；ρw为海水密度；D为桩径；ux为流体x方向的流速；CM为惯性力因数；ax为流体x方向的加速度。对波浪作用区域内沿桩长积分即可得到波浪对桩柱的水平力。本文波浪荷载计算时采用的水质点运动速度、加速度项均由随机仿真模拟生成。

1.4 模型及荷载参数

单桩基础、导管架基础海上风机有限元模型的基本参数如表3所示。

表3 单桩基础、导管架基础海上风机有限元模型的基本参数

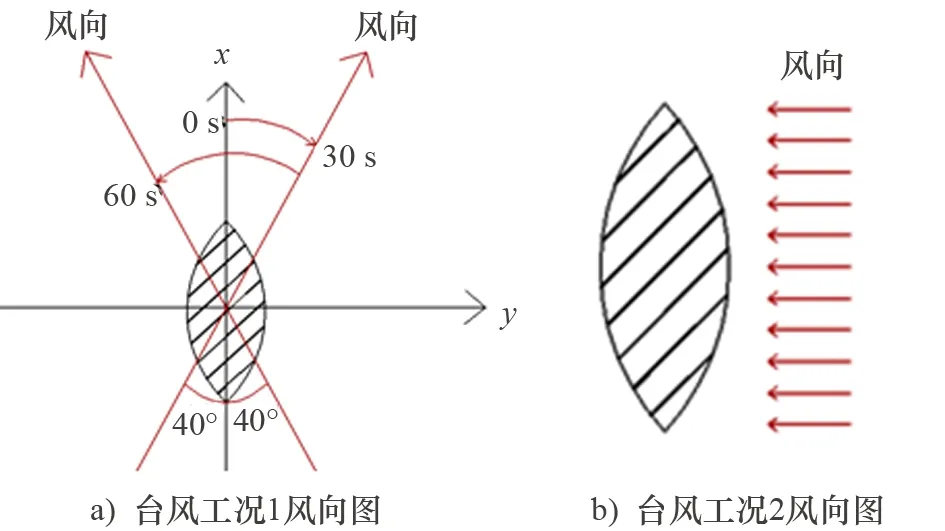
图4 台风工况风向图

图5 导管架基础风机初始受荷方向

在采用叶素-动量理论计算叶片风荷载时，由于参考技术手册仅提供了气流攻角在40°范围内变化时升力因数CT和阻力因数PD的取值，除计算在台风工况1(见图4a))下台风风向在40°范围内变化时叶片的风荷载外，为了弥补台风风向只在±40°小范围内变化对风机实际受荷的低估，另增加了台风工况2(见图4b))，气流攻角保持为90°，此种工况下台风中的风机承受最大风荷载。风、波浪、流荷载相关参数如表4所示。

表4 风、波浪、流荷载相关参数表

相对轴对称结构的单桩基础风机结构，导管架基础风机数值模型需设定初始加载方向，如图5所示，设定为沿桩基布置的边长方向加载，4根桩基桩位设定为左上、右上、左下和右下。

2 动力响应分析及计算结果

基于已构建的单桩和导管架基础海上风机结构的动力计算有限元模型，计算台风工况下风机结构的动力响应特征，具体计算结果分析如下。

2.1 自振频率、振型及参数敏感性分析

2.1.1 自振频率与振型

由表5可知：与单桩基础相比导管架基础整体刚度大，自振基频大。两种典型结构模型均为对称结构，一、二阶频率相同，分别为0.230 4 Hz、0.352 3 Hz。在风机整体结构初步设定时，需确定其一阶频率远离风机1P和3P的频率带范围[10]。

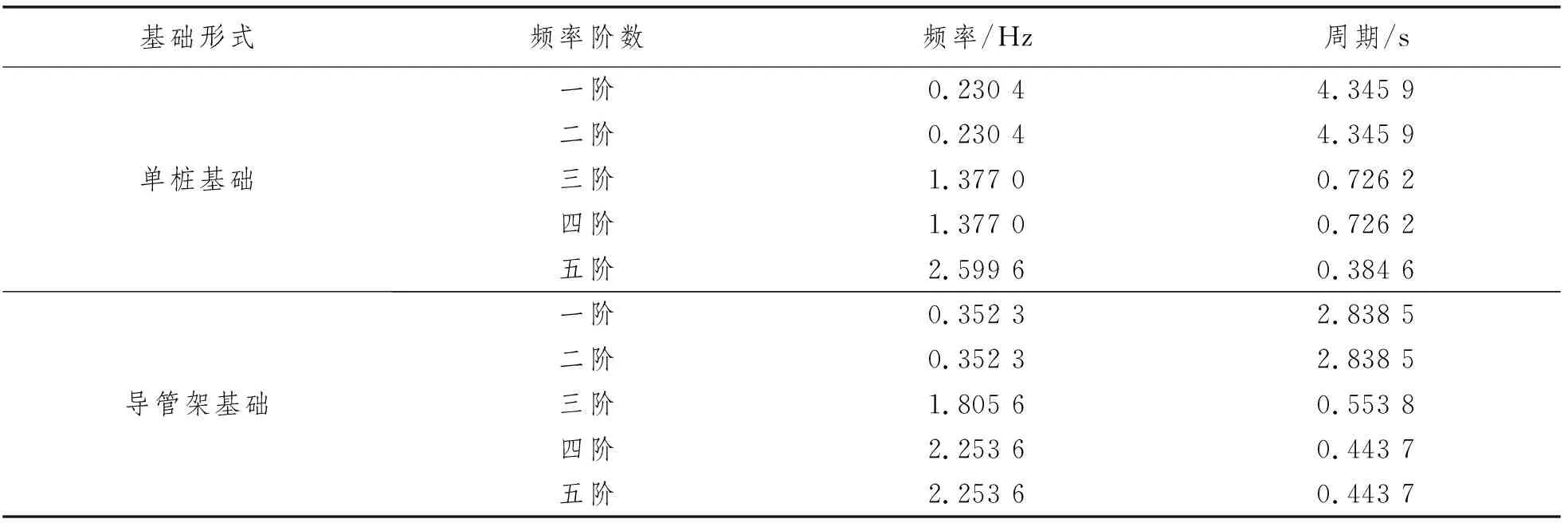
表5 单桩基础和导管架基础风机模型前五阶自振频率

由图6可知：单桩基础风机前五阶振型均为x-z平面或y-z平面的面内弯曲。从图7可知：导管架基础一、二阶振型为塔筒的单向弯曲；三阶振型表现为导管架部分绕z轴的扭转；四、五阶振型较为复杂，一方面塔顶发生小位移，塔身发生弯曲，位移较大，另一方面，导管架部分沿塔身弯曲方向发生位移。因此，导管架基础不仅需加强塔筒的抗弯性能，还需提高导管架部分的抗扭和抗水平侧移能力。

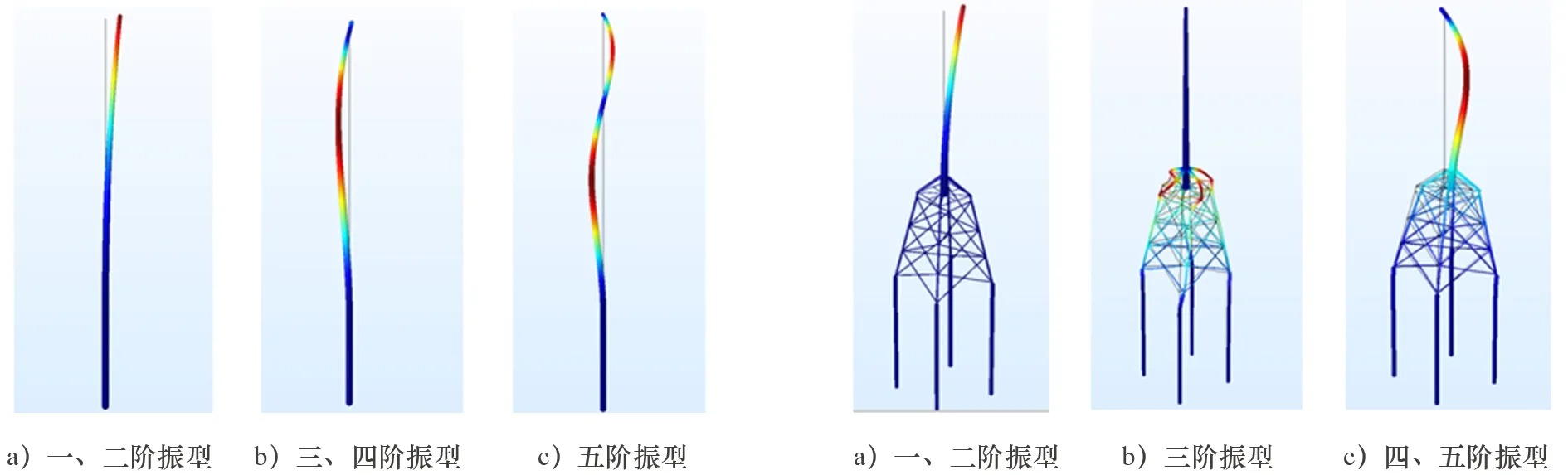
图6 单桩基础风机前五阶振型图 图7 导管架基础风机前五阶振型图

2.1.2 自振频率参数敏感性分析

海上风机属于高耸动力敏感结构，塔筒高度和壁厚对风机整体动力响应影响较大。在原始轮毂高度(95.5 m)的基础上，以1 m为单位，使塔筒高度分别增加和减少5 m，研究塔筒高度对两种基础形式风机自振频率的影响；在原始塔筒壁厚(25 mm)的基础上，以1 mm为单位，分别增加和减少5 mm，研究塔筒壁厚对自振频率的影响。计算结果如图8所示。

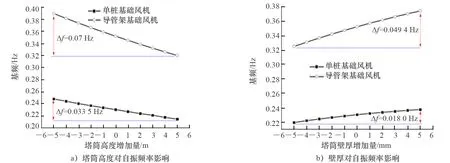
图8 塔筒高度、壁厚对自振频率影响分析

在塔筒高度变化10 m范围内，单桩基础风机频率变化量为0.034 Hz，导管架基础风机频率变化量为0.070 Hz，与一阶自振频率相比，单桩基础频率变化14.5%，导管架基础频率变化19.9%；在塔筒壁厚变化的10 mm范围内，单桩基础风机频率变化量为0.018 Hz，导管架基础风机频率变化量为0.049 Hz，与一阶自振频率相比，单桩基础频率变化7.8%，导管架基础频率变化14.0%。由此可知：塔筒高度和壁厚对单桩基础和导管架基础风机的自振频率影响较大，相比之下，导管架基础形式更加敏感。

2.2 风机动力响应分析

基于构建的数值模型，对两种典型风机动力响应过程中桩基泥面和轮毂点转角、位移进行计算分析，动力响应分析计算时程均为60 s。

2.2.1 台风工况1：气流攻角在±40°范围内变化

(1) 桩基泥面处转角、位移动力响应分析。气流攻角变化时，两种典型结构海上风机桩基泥面处转角、位移动力响应结果分别如图9和图10所示。选取导管架基础中动力响应最大的右上桩与单桩基础进行对比分析可知，导管架基础桩基泥面转角和泥面位移均明显小于单桩基础的响应值。导管架基础右上桩最大泥面转角接近0.026°、最大泥面位移接近0.007 m，而单桩基础的最大泥面转角接近0.180°、最大泥面位移为0.023 m。导管架基础风机4根桩的动力响应也存在较大差别，右上和右下两根桩的泥面转角响应规律基本一致，且响应较大。左下桩振荡过程最为稳定，泥面转角和泥面位移分别在0.004°和0.001 m附近振荡。4根桩的响应程度与荷载作用方向有很大的关系，处在上风向的桩位移响应小，处在下风向的桩位移响应大。

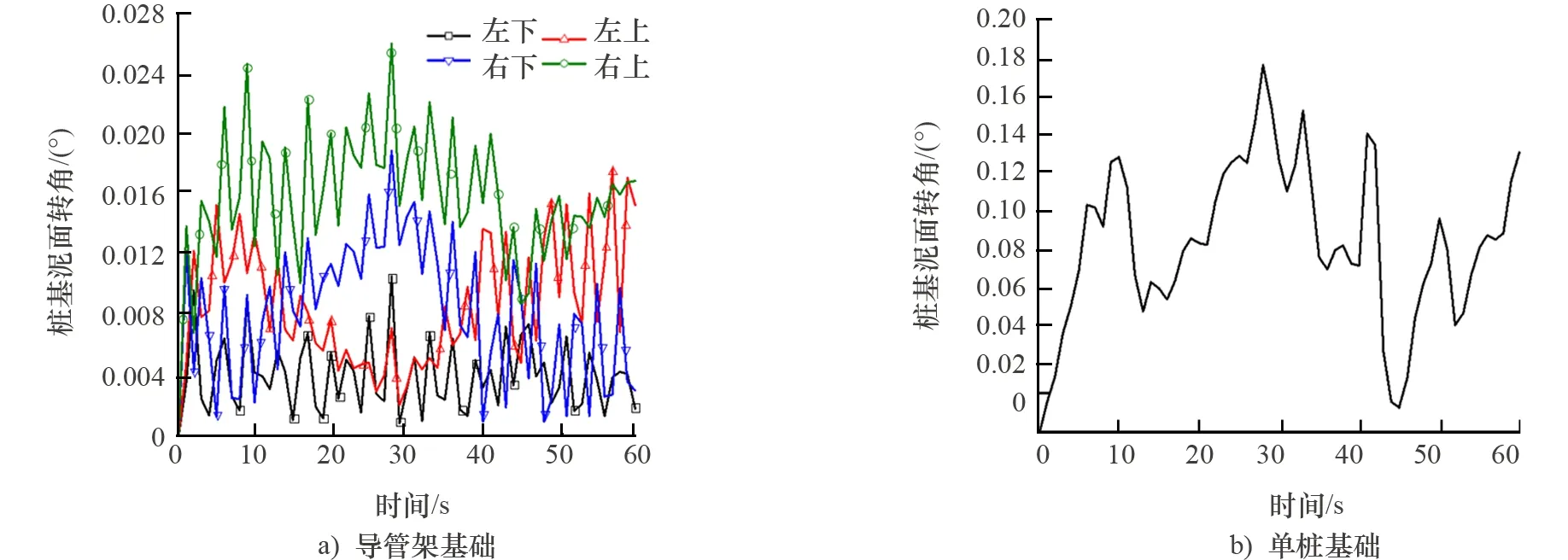
图9 台风工况1时两种典型结构风机桩基泥面处转角时程图

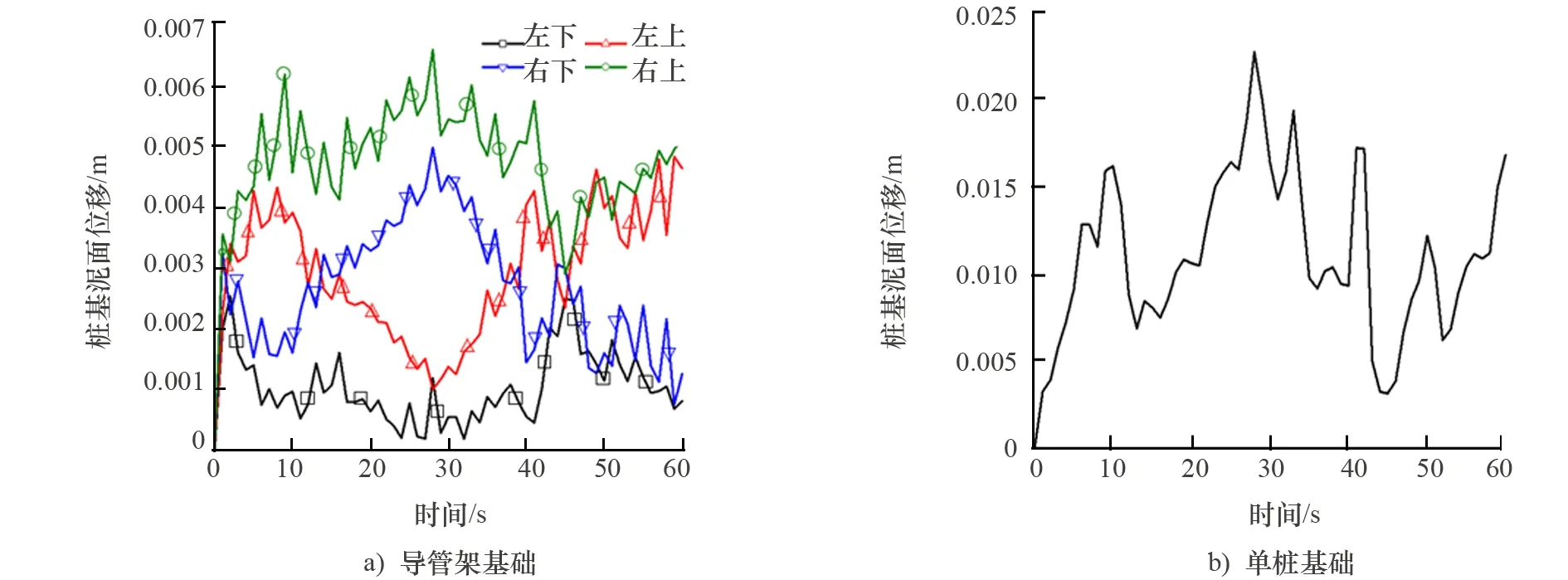
图10 台风工况1时两种典型结构风机桩基泥面处位移时程图

(2) 轮毂点转角、位移动力响应分析。两种典型结构海上风机轮毂点转角、位移动力响应计算结果如图11所示。可以看出：单桩基础风机轮毂点的转角、位移响应幅度明显更大，分别达到2.20°和2.5 m，而导管架基础风机轮毂点最大转角、位移仅为1.24°和1.0 m。

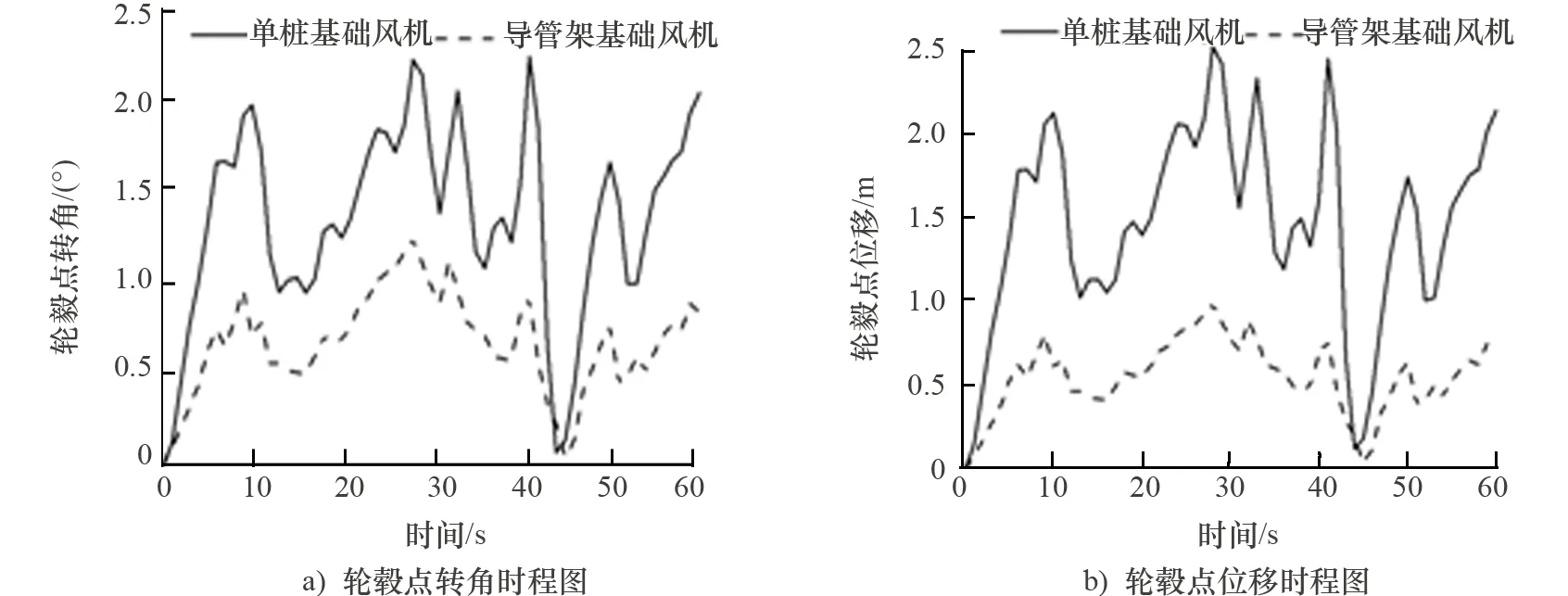
图11 台风工况1时两种典型结构风机轮毂点转角、位移时程图

2.2.2 台风工况2：气流攻角保持90°恒定

(1) 桩基泥面处转角、位移动力响应分析。两种典型结构海上风机桩基泥面处转角、位移动力响应计算结果分别如图12和图13所示。选取导管架4根桩中泥面转角响应最大的右上桩与单桩基础进行对比分析，与台风工况1类似，单桩基础风机的动力响应明显大于导管架基础风机的动力响应。导管架基础右上桩基泥面转角大概在0.022°上下振荡，而单桩基础桩基泥面转角在0.250°上下振荡，是导管架基础右上桩平衡位置的11.4倍；导管架基础右上桩基泥面位移在0.007 m上下振荡，单桩基础桩基泥面位移在0.030 m上下振荡，是导管架基础右上桩的4.3倍。

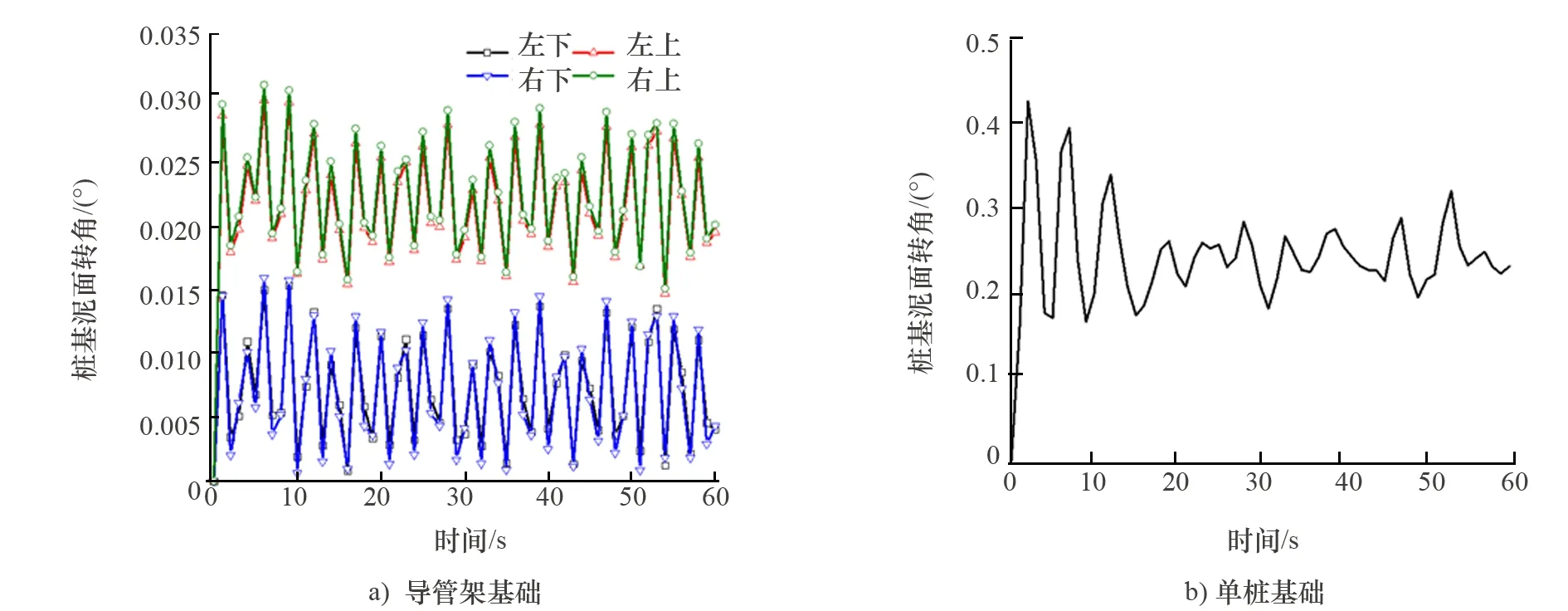
图12 台风工况2时两种典型结构风机桩基泥面处转角时程图

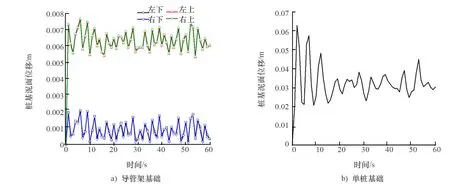
图13 台风工况2时两种典型结构风机桩基泥面处位移时程图

(2) 轮毂点转角、位移动力响应分析。图14为两种典型结构海上风机轮毂点转角和位移的动力响应计算结果。与台风1工况计算结果类似，单桩基础风机轮毂点转角、位移响应程度明显大于导管架基础：单桩基础轮毂点转角、位移平衡位置分别在3.4°和3.5 m附近；导管架基础风机轮毂点转角、位移平衡位置分别在1.5°和1.2 m附近。

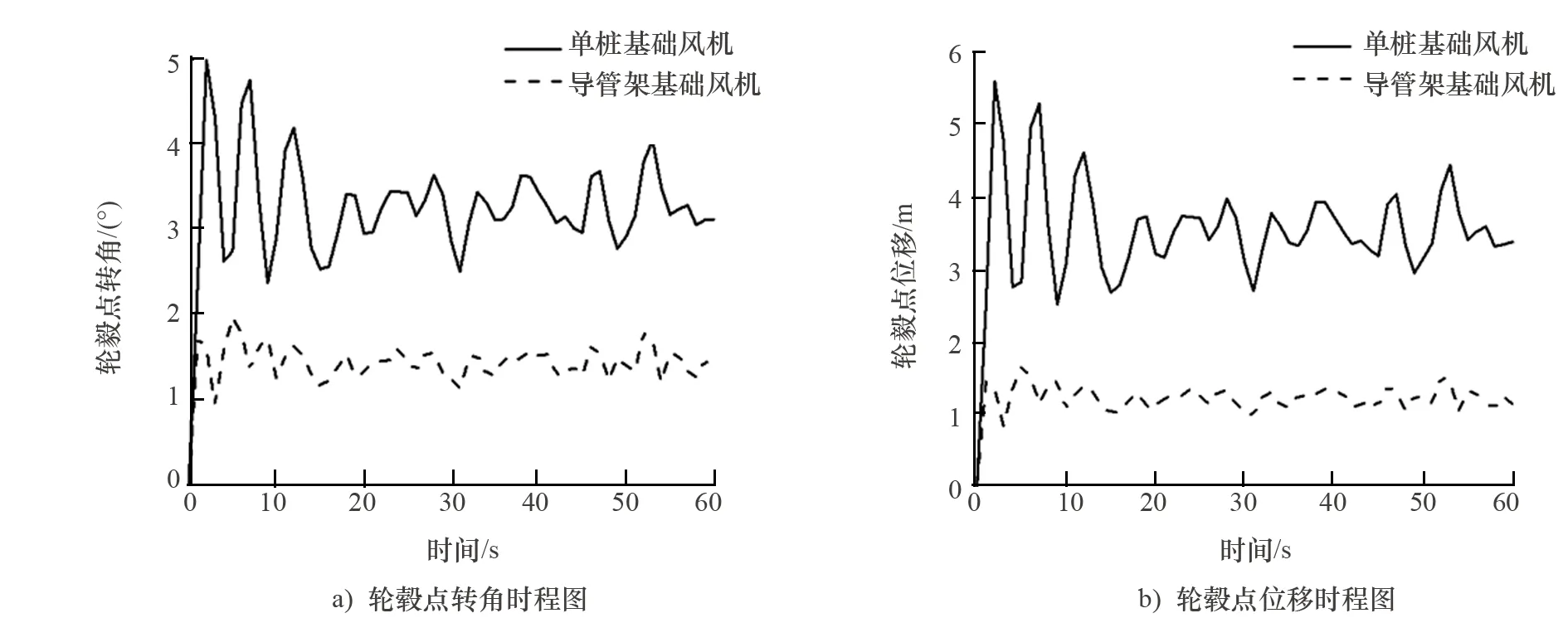
图14 台风工况2时两种典型结构风机轮毂点转角、位移时程图

不论是在台风工况1还是台风工况2条件下，与单桩基础形式相比，导管架基础刚度大，在台风环境中动力响应更小，抵抗动荷载的能力更强。相对而言，两种典型风机结构在桩基泥面处动力响应相差大，而在轮毂点动力响应相差较小。

3 结 论

基于COMSOL有限元软件建立了大直径单桩基础和导管架基础海上风机整体结构的三维数值模型，计算在两种台风工况下风机桩基泥面转角、位移和轮毂点转角、位移的动力响应，主要得出以下结论：

(1) 与单桩基础风机相比，导管架基础风机整体刚度大，基频大，对塔筒高度、壁厚参数变化更敏感。

(2) 在极端台风工况条件下，导管架基础风机的动力响应明显小于单桩基础风机。台风环境越恶劣，导管架基础形式的优势越明显。因此，在强台风区域开发风电建议采用导管架基础形式。