缠绕机器人CAD/CAM系统设计及应用

许家忠 刘美军，2 孙 栋

1.哈尔滨理工大学自动化学院，哈尔滨，150080 2.哈尔滨理工大学机械动力工程学院，哈尔滨，150080

0 引言

在复合材料成形技术中，纤维缠绕成形可设计性强，是生产复合材料制品的重要技术[1]。主缠绕机是纤维缠绕复合材料制品的核心装备，多轴、多运动轴联动的缠绕机逐渐成为标配装备，但存在自由度低、适应性及柔性差、无法自动缠绕成形复杂异形复合材料制品等问题[2]。机器人具有自由度多、通用性好、精度高和可扩展性强等优点，特别适合复杂形状复合材料制品的高精度自动缠绕成形，将机器人技术应用于缠绕已经成为发展趋势之一。

国外已对基于机器人技术的复合材料制品成形装备开展了研究。法国MF Tech公司研发了Pitbull和Fox两种多轴机器人缠绕控制系统，实现了管道、压力容器、复杂异形结构件的缠绕；加拿大Compositum公司自主研发了可用于多种型号机器人和数控系统的全自动缠绕控制系统，实现了复合材料容器(天然气、氢气储罐)的生产[3-4]。除缠绕装备外，国外对缠绕配套的CAD/CAM软件的研发也处于领先水平。比利时Materials公司开发的 CADWIND软件，可实现复合材料芯模CAD建模、缠绕线型生成、纤维缠绕过程的三维动态仿真，适用于2～6轴纤维缠绕机床。英国Crescent Consultants Ltd.的CADFIL软件是一个集成CAD/CAM/CAE的三维复合材料纤维缠绕的专业模拟软件，其功能与CADWIND软件相似。

我国目前对机器人缠绕装备的研究较少，纤维缠绕CAD/CAM技术研究也起步较晚，但不少研究单位也开发了纤维缠绕CAD/CAM软件[4]，如哈尔滨理工大学自主研发的玻璃钢管道CAD/CAM软件已成功用于玻璃钢管道自动化生产线；浙江大学研发的缠绕弯管CAD/CAM软件——ElbowCAD填补了国内弯管缠绕CAD/CAM的空白；哈尔滨工业大学开发的WindSoft缠绕软件在纤维缠绕技术研究和产品制造中得到广泛应用。

目前，国外已实现复合材料制品机器人缠绕成形，但复杂异形复合材料制品机器人缠绕CAD/ CAM软件由于技术封锁，还未开放。国内多数CAD/CAM软件只适用于传统机床的常规芯模缠绕设计，或只针对某一特定形状的异形件缠绕设计，对复杂异形件缠绕设计不具通用性。针对上述问题，笔者提出局部曲面缠绕法与机器人缠绕轨迹规划方法，并开发了一套集复杂异形件缠绕设计与制造于一体的机器人缠绕CAD/CAM系统。

1 缠绕机器人系统

如图1所示，缠绕机器人系统由六轴机器人、带张力控制器的纱架、与机器人同步控制的扩展轴(芯模主轴)、控制系统和上位机软件组成。上位机软件分为CAD、CAM和仿真三个子系统。缠绕机器人具体参数如下：最大出纱速度50 m/min；缠绕行程2 000 mm；轨迹精度±0.2 mm；机器人关节1～6的最大角速度分别为2.146 8 rad/s、2.007 1 rad/s、1.954 8 rad/s、3.124 1 rad/s、3.002 0 rad/s、3.822 3 rad/s。

图1 缠绕机器人系统Fig.1 Systematic structure of winding robot

2 缠绕机器人CAD系统

缠绕机器人CAD系统的主要作用是芯模模型建立和缠绕线型设计，为CAM的实施提供相应的原始数据。系统接受两种建模方式。第一种是针对常规型芯模的建模方法——几何参数直接输入法，例如，建立一个气瓶模型，只需要输入直段长度、直段半径、封头半径、封头高度、极孔直径与封头类型等。第二种是针对复杂异型件的建模方法——外部DXF参数文件导入法，该方法在外部CAD图形软件如AutoCAD、Pro/E建立模型后，先将生成的DXF文件导入系统完成建模，再对几何芯模表面进行网格化布点。线型设计采用的是基于纤维稳定缠绕理论、网格理论、曲面拟合理论的局部曲面缠绕法。

2.1 纤维稳定缠绕条件

纤维稳定缠绕条件包括：纤维不滑移判定公式[5-6]、纤维不架桥判断条件[7-8]。

图2中，芯模表面任意落纱点P所受的沿曲率半径方向c的力Fr分解为两个方向的力：Fn(垂直于芯模表面，沿曲面P点的主法向量n的负方向)和Fg(垂直于P点纤维的切线t，沿着测地线向量g的方向)。Fg使纤维产生滑移趋势，当纤维与芯模表面存在摩擦力时，摩擦力Fw与Fg方向相反，因此若要使纤维稳定不滑纱，最大摩擦力|Fw|应该大于|Fg|。

图2 曲面上P点受力分析Fig.2 Analysis of force at point P on the surface

定义滑移系数λ：

λ=|Fg|/|Fn|=Kg/Kn

(1)

式中，Kg、Kn分别为P点的测地曲率(短程曲率)和法曲率。

P点纤维受到最大的摩擦力为

Fw=|Fw|=μsFn=μs|Fn|

(2)

式中，μs为静摩擦因数。

因此纤维在芯模表面不滑移判定的稳定方程为

λ≤μs

(3)

纤维不架桥的判断条件，即纤维拉紧时正压力Fn的方向决定纤维是否发生架桥，若Fn的方向为图2中的反方向即纤维远离芯模表面的方向，则将产生架桥，反之，不产生架桥。于是可得纤维不架桥的条件：曲面上该点的法曲率与单位法矢量方向相反，即

Kn<0

(4)

2.2 局部曲面缠绕法

局部曲面缠绕法就是将不易用精确参数方程表示的芯模表面进行网格化，以局部网格拟合的曲面为计算单位，根据缠绕角全程稳定以及纤维稳定缠绕等条件，确定一系列网格节点为纤维缠绕的离散落纱点轨迹。

曲面拟合的方法有多种，本系统采取的是参数多项式拟合法[9]。参数多项式拟合曲面可以通过改变参数多项式的次数和系数获得新的多项式，从而应对不同的拟合要求。参数多项式可以无穷次可微，因而曲面能够足够光滑，且其函数值以及各阶导数计算相对简单，易于程序化。综合考虑拟合精度与计算速度后确定多项式次数为3，相应多项式曲面方程为

z=f(x,y)=a1+a2x+a3y+a4x2+
a5xy+a6y2+a7x3+a8x2y+a9xy2+a10y3

(5)

三次多项式拟合曲面最少需要10个已知点[10]，因此根据当前落纱点位置、缠绕角的范围(0°～90°)以及出纱方向，确定图3所示的4×4单位计算网格，选其中的10个网格节点(圆点，其中，P点为当前落纱点，其余9个点为下一个落纱备选点)进行曲面拟合，得到曲面参数方程。

图3 4×4单位网格Fig.3 4×4 unit grid

设li(xi，yi)为曲面上的任意一点(i=1，2，…，10)，对于任意li都满足如下线性关系：

(6)

其中，aj(j=1，2，…，10)为三次多项式的系数；bj(li)为三次多项式的空间的一组基，bj(li)=xpyq，0≤p+q≤3。基的完整形式为

(7)

(8)

分解式(8)得

(9)

展开式(9)得

(10)

J=1，2，…，n

将式(10)改写成矩阵形式得

BBTA=BZ

(11)

AT=[a1a2…an]ZT=[z1z2…zn]

根据式(11)可以求出aj，从而得到拟合曲面方程z=f(x,y)。

在拟合曲面上对备选落纱点进行分析，根据前述判断条件选取最稳定落纱点，即滑移系数最小且不架桥的点。若存在多个滑移系数最小且不架桥的点，则选择与前一落纱点相比，缠绕角变化最小的点；若所有点均不符合稳定缠绕条件，则扩大局部网格范围，通常的做法是根据缠绕角是否大于45°选择2倍纵向或横向网格距离。最后，将每个顺序单位网格中最稳定落纱点进行连接，即可得到整体离散的落纱点轨迹。图4为局部曲面缠绕法实施流程图。

图4 局部曲面缠绕法实施流程图Fig.4 Flow chart of local surface winding method

3 缠绕机器人CAM系统

CAM系统的主要作用是根据设计完成的离散落纱点轨迹，计算机器人末端装卡的丝嘴的缠绕运动轨迹，并自动生成机器人可识别的执行代码文件。

3.1 机器人缠绕路径规划

网格后置处理法[11]不受限于芯模表面方程且对不同形状的芯模处理难易程度相同，特别适合异形件缠绕的路径规划。该方法首先根据离散落纱点轨迹、缠绕过程中悬纱长度约束来求取出纱点，然后通过计算相邻出纱点的位置，得到丝嘴缠绕路径坐标。本系统借鉴此方法对CAD系统所得离散落纱点轨迹进行后处理，得到机器人基坐标下离散缠绕路径，每个路径点坐标为(X，Y，Z，A，B，C，θE)，其中，(X，Y，Z)为丝嘴在基坐标内的位置；(A，B，C)为丝嘴在基坐标内的姿态；θE为主轴转角。

然后根据精度要求，通过判断相邻两路径点之间的距离与阈值，选择性地对路径点进行插补规划，并进行直线插补、NURBS曲线插补等细分处理。应用逆运动学理论将所有基坐标形式的路径点转换为由每个轴的转角组成的关节坐标 (θ1，θ2，θ3，θ4，θ5，θ6，θE)。

3.2 机器人缠绕速度规划

缠绕速度不仅影响缠绕效率，还影响缠绕制品的质量。湿法缠绕中，丝嘴运动过快会导致纤维浸胶不足。另外，主轴(缠绕制品的芯模)转速过高容易造成芯模表面的胶液在离心力作用下飞溅，制品含胶量不足势必会影响质量；干法缠绕中，机器人缠绕速度受限于机器人速度上限与设备缠绕张力控制能力,因此需要对机器人缠绕速度进行规划。最常见的缠绕速度规划方式是快速缠绕，即在自主设定的大速度下快速缠绕，该方法效率最高，对于缠绕任何形状的芯模都适用。除此之外，还有主轴恒转速与恒出纱速度两种规划方式。主轴恒转速缠绕时，机器人运行最稳定，但缠绕速度最低；恒出纱速度缠绕时，缠绕张力控制最稳定。

对于缠绕运动，我们要求机器人的运动是准确、连续且平滑的。缠绕时，每个关节轴和主轴需要同时到达各丝嘴路径点，因此各个轴的各段路径所需的时间相同[12]。尽管对每个轴指定了相同的时间间隔，但对于某个特定的轴而言，其期望的转角函数与其他轴函数无关[13-15]。对于任意轴，其各个轨迹点的位置是已知的，t0时刻的值为该轴的初位置θ0，tf时刻的值为该轴的目标位置θf，如图5所示，有多种光滑函数θ(t)可对该轴进行轨迹规划。

图5 光滑函数曲线Fig.5 Curves of smooth function

本系统光滑函数θ(t)选用五次多项式函数

对应的速度与加速度为[16-17]

根据相邻两丝嘴轨迹点位置得

根据相邻两丝嘴轨迹点速度、加速度

解得θ(t)的5个系数：

(1)主轴恒转速缠绕时，有

tf=(θE(tf)-θE(t0))/ωm

其中，ωm为主轴角速度；θE(t0)为当前落纱点时的主轴转角；θE(tf)为下一个落纱点时的主轴转角。

(2)当快速度缠绕时，有

其中，ωmaxk为第k(k=1，2，…，6) 关节或主轴的最大速度；θk(t0)为当前落纱点时第k关节或主轴的转角；θk(tf)为下一个落纱点时第k关节或主轴的转角。

(3)当恒出纱速度缠绕时，有

其中，ωn为出纱角速度；α为实时缠绕角。

确定速度规划方式后即可求得a1、a2、…、a5，从而得到6个关节轴与主轴经过所有丝嘴轨迹点间的各光滑函数θk(t)和θE(t)的表达式，进而可得到机器人整个缠绕过程的关节空间轨迹函数：

f(t)=(θ1(t),θ2(t),θ3(t),θ4(t),θ5(t),θ6(t),θE(t))

(12)

对其求导，可得各轴速度函数：

(13)

将路径更新率f=1/t代入式(12)、式(13)可得每个周期的机器人关节坐标与速度。

3.3 机器人执行代码自动生成

机器人执行代码自动生成是将虚拟规划的机器人缠绕轨迹数据转化为实体机器人程序指令。根据KUKA机器人语言格式，通过开发高级语言程序VC，运用MFC中CFileDialog类对程序模板文件进行操作，将各轴转角更新至相应指令语句中，保存为指定的文本文件“RobotWind.src”。

4 系统仿真功能

基于OpenGL搭建缠绕仿真环境，可实现缠绕线型仿真与丝嘴运动位姿仿真。线型仿真能三维显示任意时段纤维在芯模表面排布规律，比如切点数、交叉点数等。通过丝嘴运动仿真能全程显示丝嘴相对芯模的位姿，方便对丝嘴运动进行干涉检查，防止因参数设置不正确或丝嘴轨迹规划不合理等原因，造成丝嘴运动时与芯模发生干涉。

5 机器人缠绕CAD/CAM系统应用实例

5.1 建模

组合回转体由球段、圆柱段以及衔接段组成，具体参数如图6a所示；将芯模网格化布点，网格节点数为24×58，如图6b所示。

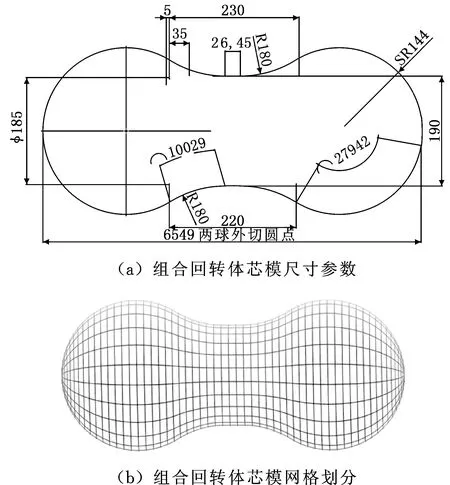
图6 组合回转体芯模Fig.6 Mandrel for combined revolution

5.2 缠绕仿真

缠绕线型如图7所示，球段采用测地线缠绕(μs=0)，圆柱段与过渡缠绕采用非测地线缠绕(μs>0)，起始缠绕角为74°，纱线宽度为40 mm。机器路径采用封闭圆柱形式进行规划，安全距离设为50 mm，快速缠绕速度设为50%机器人额定速度，仿真缠绕过程未发生运动干涉。

图7 缠绕线型设计仿真图Fig.7 Simulative winding pattern

5.3 缠绕实验

实际缠绕采用机器人手抓丝嘴单纱缠绕，7 N恒张力控制。整个缠绕过程中未出现滑纱、纱线架桥情况，缠绕线型准确，如图8所示，实际纱宽41.97 mm与设计纱宽40.00 mm的误差在±2 mm以内。

图8 实际缠绕线型Fig.8 Windng patterns of combined revolution

机器人实际缠绕路径更新率f=100 Hz，即一个伺服周期为10 ms。对缠绕过程中机器人各关节速度采样分析，图9a所示为缠绕组合回转体桶身段时某100个伺服周期内机器人各个关节的速度变化曲线，可知缠绕组合回转体桶身过程中，机器人的关节1按最快速度转动，且基本保持匀速，其余关节根据关节1的速度大小各自进行速度调节，以满足所有关节同时到达丝嘴轨迹点的要求。出现这种速度规律的原因是，当机器人缠绕组合回转体桶身段时，主要的运动是执行丝嘴左右移动，即沿机器人Y轴方向(组合回转体轴向)的运动量最大，而关节1是主要承担机器人Y方向位移的关节。图9b所示为缠绕组合回转体封头段时，某100个伺服周期内机器人各个关节的速度变化曲线，图中显示，转动速度最大的是关节4，其次是关节2、关节5，出现这种速度规律的原因是,当机器人缠绕组合回转体封头段时，主要的运动不仅有丝嘴沿机器人X轴方向运动，还有丝嘴绕机器人X轴的转动。其中，关节2是主要承担机器人X方向位移的关节，关节4与关节5是主要承担机器人绕X轴旋转的关节。

图9 机器人关节速度Fig.9 Velocity of robotic joints

6 结论

针对机器人缠绕复合材料复杂异形件问题，基于局部曲面缠绕法与机器人缠绕轨迹规划方法，建立了一套缠绕机器人CAD/CAM系统。局部曲面缠绕法基于芯模表面网格节点的缠绕理论，利用曲面拟合方法，通过判断拟合曲面上备选点是否符合稳定缠绕条件确定落纱点轨迹，能有效解决复杂异形件缠绕线型设计问题。机器人缠绕轨迹规划方法能够针对3种不同的缠绕速度，计算机器人缠绕的光滑关节空间轨迹。结合一个组合回转体芯模缠绕的应用实例，介绍了机器人缠绕CAD/CAM系统的功能。实例验证了系统对异形件纤维缠绕的适应性、缠绕算法的可行性。