基于多参量模型的光纤陀螺温度误差补偿

戴邵武，郑百东，李文国，戴洪德

(1.海军航空大学，烟台 264001；2.中国人民解放军92840部队，青岛 266000)

0 引言

光纤陀螺以全固态、寿命长、可靠性高等优点，成为了捷联惯导系统的核心部件，被广泛应用于军事和民用领域[1-3]。组成光纤陀螺的光纤环、Y波导等光学器件对环境温度的变化非常敏感，温度变化引起的非互易性相移是制约光纤陀螺输出精度的关键因素之一[4-5]。

解决温度漂移的方法包括改进陀螺的结构、光纤环的绕制方法，使其对温度不敏感；采用温控装置使陀螺工作在一个恒温的环境;通过热力学实验和分析建立陀螺的静、动态温度漂移模型[6-9]。其中建立温度漂移模型进行温度误差补偿，可以在不增加成本的基础上提高陀螺精度，具有重要的研究意义。文献[10]将陀螺输出自回归项和温度梯度滞后项引入到光纤陀螺温度建模中，提出了一种温度漂移多变量模型，并通过实验验证了模型的有效性，但该方法未对温度的高低和温度变化情况做分段讨论；文献[11]将陀螺温度特性分成低、中、高3个温度区间，仅以温度项作为建模参数，分别建立不同阶次的分段拟合模型，并对采集到的温度漂移数据进行补偿，验证了方法的可行性。

本文在文献[10]和文献[11]的基础上，通过温度各相关项与陀螺漂移误差之间的相关性分析提取建模参数，将温度与温度速率的乘积项、温度梯度滞后项引入到模型参数中，建立了多参量联合模型，弥补了仅将温度项作为建模参数的不足；并根据不同的温度变化情况分别建立了升温模型和降温模型，提高了模型精度。利用OFG温箱实测数据验证了补偿方案的有效性，并与传统建模方法进行对比分析。

1 温度漂移实验与特性分析

本实验以某型惯性组件的光纤陀螺为研究对象，将陀螺组件安装在带有温控箱的水平转台上；为消除陀螺的标度因数对陀螺温度漂移的影响，必须保证陀螺的输入角速度为0[12]。因此，将陀螺输入参考轴置于水平面内，并使参考轴与东向之间夹角为0，即可满足条件φs=0。采用热循环的试验方式，陀螺启动后，调节温箱，不断升温降温，每隔1s，输出一组温度(T)和陀螺输出数据(D)，实验测量(-10～50)℃温度区间变化时的零漂，温度变化速率为(3～5)℃/min，采集升温和降温过程的陀螺输出数据，如图1和图2所示。

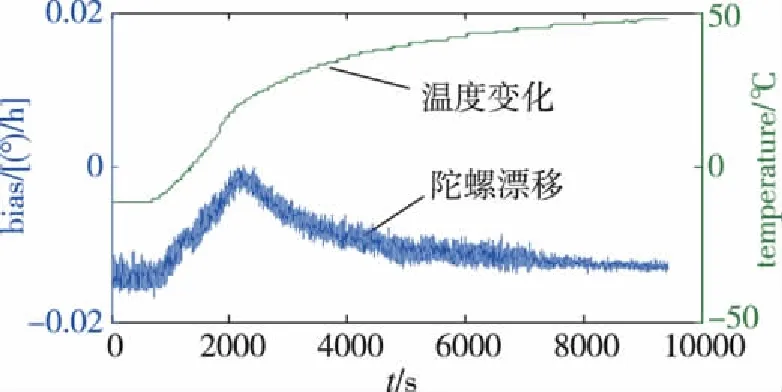
图1 升温阶段光纤陀螺温度与零漂误差Fig.1 Temperature and bias of FOG in temperature-rise stage

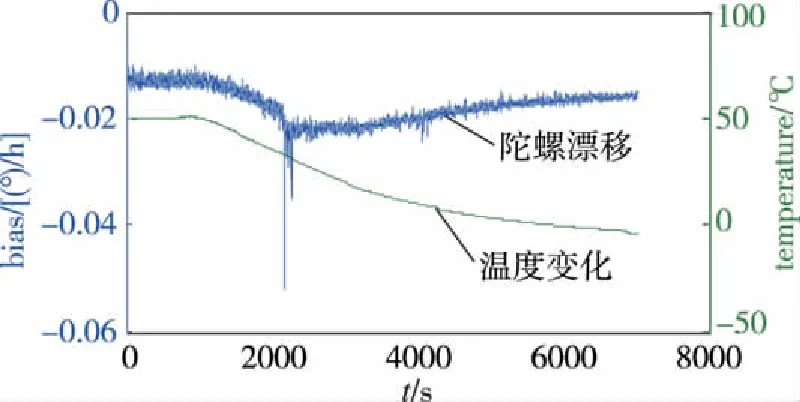
图2 降温阶段光纤陀螺温度与零漂误差Fig.2 Temperature and bias of FOG in temperature-fall stage

其中采集到的温度项为温箱中传感器的温度，代表光纤陀螺所处环境温度的变化；通过温度项数据平滑求导可获得温度速率(dT/dt)和温度二次速率项(d2T/d2t)，进而通过运算获得温度与温度速率乘积项。由于陀螺腔体内部的温度场十分复杂，很难获得精确的温度梯度数据，本文假定温箱中的温度均匀，根据热传递定律，温箱内环境温度的变化是导致陀螺腔体由外而内的温度场产生温度梯度的原因。于是本文定义单位时间内陀螺壳体环境温度的变化ΔT作为温度梯度的近似，由于这个温度梯度在陀螺腔体由外而内的传播过程中存在一定的时间延迟，定义ΔT(t-n)为温度梯度分布的n秒滞后。为分析陀螺漂移和各温度相关项之间的相关性程度，对温度因素和光纤陀螺的温度漂移项之间的相关性进行分析。

用Pearson相关性系数r衡量2组变量之间的相关性可以表示为[13-14]

(1)

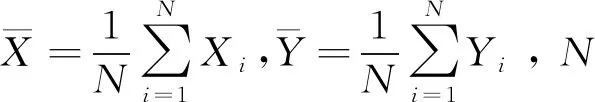
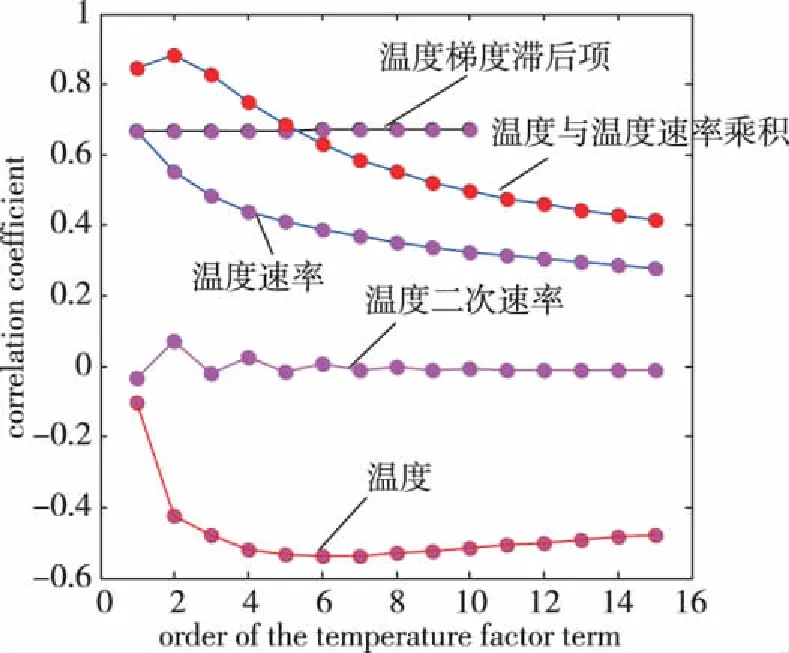
图3 升温阶段陀螺漂移与各温度相关项相关系数Fig.3 Correlation coefficient between gyro drift and temperature related terms in temperature-rise stage

分析发现，升温阶段光纤陀螺的温度漂移与温度项、温度速率项、温度梯度滞后项及温度与温度速率的乘积项呈现出显著相关，温度二次变化速率与陀螺的零漂误差基本上没有相关性。升温阶段建模时可选用温度项、温度速率、温度梯度滞后项及温度和温度速率乘积项作为建模参数。

对降温过程中陀螺漂移与各温度相关项进行Pearson相关性系数分析，分析结果如图4所示。从图4中可以看出，降温阶段陀螺漂移与温度项为正相关，而升温阶段相关性为负相关；降温阶段温度梯度滞后项、温度变化速率、温度二次变化速率项与光纤陀螺零漂输出相关性，随着幂次增加呈震荡性减小；温度与温度速率的乘积项与陀螺的零漂输出之间相关性弱，这与升温阶段陀螺零漂与此项呈强相关性不同；降温阶段温度梯度滞后项与陀螺零漂之间同样存在较强的相关性；所以降温阶段的建模可选择温度、温度速率、温度梯度滞后项作为建模参数。

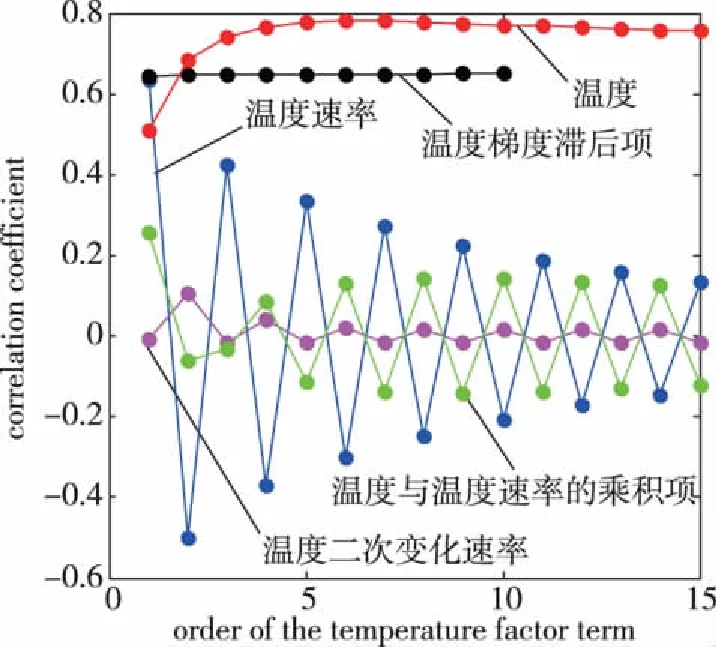
图4 降温阶段陀螺漂移与各温度相关项相关系数Fig.4 Correlation coefficient between gyro drift and temperature related terms in temperature-fall stage

2 光纤陀螺温度漂移多参量模型

光纤陀螺的一般建模方法仅表征环境温度与陀螺漂移之间的关系，通过上面的陀螺漂移与温度因素之间的相关性分析可知，这样的建模方法是片面的，无法表征温度各因素与陀螺漂移之间的关系。

考虑到温度对光纤陀螺的影响是多因素的，为提高模型的准确性，结合光纤陀螺温度特性分析，选取温度、温度速率、温度梯度滞后项及温度与温度速率的乘积项为模型参数。光纤陀螺的温度漂移模型如下形式

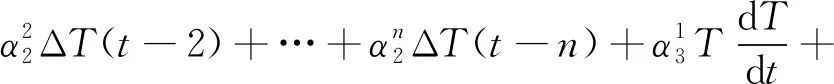
(2)

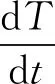
3 模型有效性验证

升温阶段时利用最小二乘法确定建模参数得

F(t)=-2.24281×10-3+6.05207×10-4T-

3.70774×10-5T2+4.17096×10-7T3-

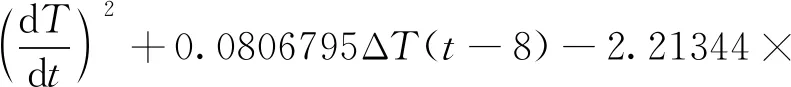
(3)

用所得到的模型对采集得到的升温过程进行补偿，补偿效果如图5所示。

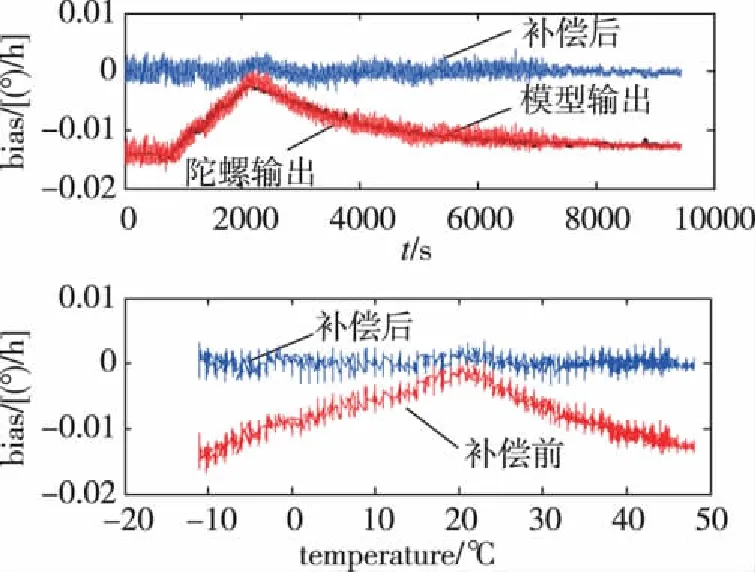
图5 多参量模型升温阶段补偿结果Fig.5 Results of multi-parameter model in temperature-rise stage

以总体均值(Ensemble Average，ENA)、总体方差(Ensemble Variance，ENV)、误差平方和(Sum of the Squared Errors，SSE)作为衡量补偿效果的指标。传统模型仅以温度项作为建模参数与多参量模型补偿前后的各指标对比如表1所示，多参量模型补偿后，误差平方和降低了95%以上。

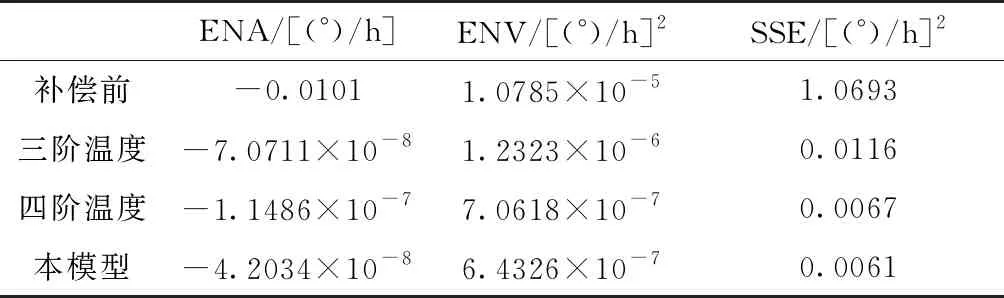
表1 升温阶段补偿前后各指标对比

补偿后的总体均值很小，说明补偿结果关于零的对称性好，惯性系统在对角速度积分时，惯性导航误差可以大大减小；均方根误差很小，说明补偿后零漂的稳定性显著提升。

对降温过程进行建模补偿，补偿结果如图6所示。降温阶段补偿后，在整个温度范围内零偏稳定，但对具有不平稳温度点漂移处的补偿效果不理想，这也是多项式拟合补偿的一个缺陷。

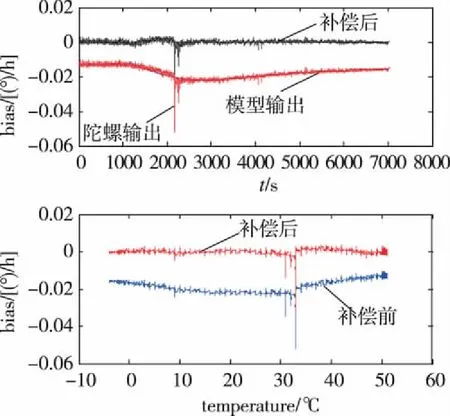
图6 多参量模型降温阶段补偿结果Fig.6 Results of multi-parameter model in temperature-fall stage

为进一步验证模型的有效性，对实验所用的光纤陀螺进行重启，采集全温度范围内的光纤陀螺温度漂移误差数据，应用所建模立的多参量分段模型对其漂移误差进行拟合补偿，结果如图7所示，可以看出该模型能够有效地抑制光纤陀螺的温度漂移误差。计算陀螺输出实测数据和模型补偿后的标准差和误差平方和：多参量模型补偿后陀螺数出的标准差从0.0046(°)/h降到9.0291×10-4(°)/h，降低为原来的20%，误差平方和从5.8326[(°)/h]2降到0.0256[(°)/h]2，降低了2个数量级。文献[12]提出的自适应神经模糊预测模型补偿后标准差为原始输出数据的25%，表明本文提出的多参量分段拟合模型与非线性模型补偿精度相当，验证了该算法的有效性。

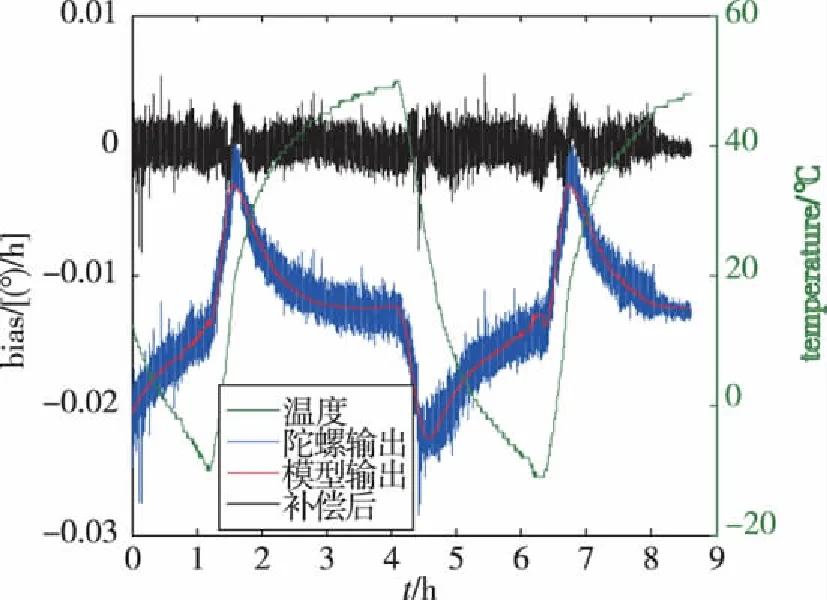
图7 多参量模型有效性验证Fig.7 Validity verification of multi-parameter models

4 结论

1) 在大量光纤陀螺温度漂移误差实测数据的基础上，研究了各温度相关项对光纤陀螺漂移误差的影响。通过相关性分析发现，温度×温度速率项、温度梯度滞后项与光纤陀螺漂移之间呈较强的相关关系，考虑将这两项作为建模参数引入到模型中。为光纤陀螺温度补偿参数的选取提供一种新思路，而非仅仅采用温度项和温度变化速率项为建模参数。

2)在升温和降温2个过程中建立了光纤陀螺温度补偿的多参量分段模型，该模型综合考虑了各温度因素对光纤陀螺漂移误差的影响，具有建模方便简单、运算速度快的优势。 以光纤陀螺的温度漂移实测数据对提出的建模方法进行了验证，补偿效果优于仅对温度项分段建模。

3)全温度段内陀螺温度漂移误差补偿结果表明，补偿后误差平方和降低了2个数量级，陀螺漂移均值、方差性能指标项稳定在零点附近，补偿效果与非线性模型相当，具有重要的工程应用价值，可考虑将其应用于陀螺温度误差的实时补偿中。