具有超图合作结构的赋权Position值
单而芳, 李 康, 刘 珍
(上海大学 管理学院,上海 200444)
0 引言
经典的可转移效用的合作对策(TU-对策)[1]通常假定任何参与者的集合都可以形成一个合作联盟,并获得相应的收益。然而,在现实生活中,由于受到不同文化宗教背景的影响以及社会阶层、技术或组织机构等因素的制约,一些联盟无法形成。为此,Myerson[2]提出并研究了以图作为合作结构的TU-对策,其中图的节点表示参与者,边表示它的两个端点所代表的参与者之间存在某种双边关系,并假定只有相互连通的参与者集合可以形成联盟。Myerson[2]通过定义“图限制对策”,并把图限制对策的Shapley值作为图对策的一个解,这就是著名的Myerson值。Myerson[2]首先给出了Myerson值的一个公理化刻画。之后,Born等[3]又给出了Myerson值的另一个公理化刻画。Myerson[4]和等van den Nouweland等[5]也把Myerson值推广到具有超图合作结构的情形。
1988年,Meessen[6]提出了图对策中另一个重要的分配规则,即Position值。为了定义Position值,他首先引入了“边对策”的概念,边对策是将每个边集作为参与者的集合,并假定当某个边集导出的子图连通时,才能形成联盟。在此基础上,首先计算边对策中每条边的值Shapley[7],然后把每条边的Shapley值平均分配给它的两个端点,给每个参与者的支付(payoff)等于分配给它的所有边Shapley值一半的和,这就是Position值。1992年,van den Nouweland等[5]进一步把Position值推广到超图对策上,并给出了无圈超图对策上Position值的刻画。该模型把图中每条边或者超图中每条超边的Shapley值平均分配给边上或者超边中的点,而不考虑每个点的交流能力或合作水平,也就是把所有参与者看成是对称的。
然而,在实际中,联盟中的参与者可能有不同的议价能力、交流能力或合作水平。Shapley[8]首先提出并研究了赋权Shapley值。联盟中对每个参与者的支付按照该参与者所占的权重比例进行分配。此后,Owen[9]、Kalai和Samet[10]、Chun[11]以及Haeringer[12]等作者对赋权Shapley值做了进一步研究,按照不同的权比例给出了不同解的形式。这些研究的共同特点是每一个参与者赋予一个正的权重,在每个联盟中按权重比例对红利进行分配。此时,参与者的权重越大,其获得的支付或分摊的成本也越多。Haeringer[13]把赋权系统推广到图对策上,并刻画了赋权Myerson值。而Slikker和van den Nouweland[14]则把Kalai和Samet提出的赋权系统推广到Myerson值,并给出了它的公理化刻画。
本文考虑超图对策上的赋权Position值。通过推广Haeringer[12]提出的赋权系统到超图对策上,并在无圈超图对策上给出了此类赋权Position值的公理化刻画。这里的赋权系统在一定程度上反映参与者的交流能力或合作水平对他获得支付或分摊成本的影响,也就是,参与者的权值越大,那么该参与者在分配中将获得更多的支付;不过,如果是成本,则分摊更少的成本。这是与经典赋权系统的一个区别。为此,我们需要寻找一个合理的方式来度量所有参与者的交流能力或合作水平。在图论和超图理论中,点的度值是一个重要概念。每个点的度值等于包含这个点的超边的数目,在某种意义上说,每个点的度值体现了该点代表的参与者的交流能力或合作水平。 因此,点的度值越大,则点代表的参与者的交流能力越强或合作水平越高。本文用点的度值来度量每条超边中每个点的交流能力或合作水平,并结合Haeringer[12]提出的用于推广Shapley值的赋权系统给出了一类新的赋权系统。该赋权系统特点是:当超边的Shapley值为正值时,包含的参与者的度值越大,其获得的支付越多;反之,当超边的Shapley值为负值时,参与者的度值越大,则其分摊的成本越少。对无圈超图对策,我们证明了赋权Position值可以由“分支有效性”、“冗余超边性”、“超边可分解性”、“拟可加性”、“弱积极性”和“弱能转换”六个性质所唯一确定。
本文第二节将介绍-对策和超图对策的一些基本定义和记号,并给出了超图对策赋权Position值的表达式。第三节对无圈超图对策上赋权Position值进行公理化刻画。第四节举例说明了超图对策中赋权Position值的六个性质。第五节对研究的结论做了总结。
1 预备知识
1.1 TU-对策
具有特征函数形式的合作对策通常称为可转移效用的合作对策,简记TU-对策[1]。TU-对策可以用一个二元组(N,v)来表示,其中N=(1,2,…,n)为参与者(player)的集合,v表示特征函数(characteristic function),它是从集族{S:S⊆N}到实数R的一个映射,即v:2N→R,且v(Ø)=0。N的任意子集S表示由S中的参与者形成的联盟(coalition)。v(S)表示联盟S的效用(worth),|S|表示集合S的基数。 如果对所有的i∈N,都有v({i})=0,我们称TU-对策(N,v)是0-规范的(0-normalized)。以下讨论中涉及的对策均指0-规范的TU-对策。

(1)
1.2 超图对策的赋权Position值
超图(hypergraph)[5]是一个二元组(N,H),其中N是点集,H⊆{e⊆N:|e|≥2}表示超边(hyperlink)集。如果超图的每条超边均是二元子集,则该超图也称为图。Hi={e∈H|i∈e}为(N,H)中包含点i的超边的集合。进一步,定义参与者i的度(degree)为|Hi|,记为di。因此di表示包含点i的超边的数目。超图(N,H)中的每一条超边e∈H可以表示一个conference结构[5],只有参加同一个conference结构[5]的参与者才可以形成特定交流。在实际中,超边可以代表某种社会组织,例如:行业协会和社团等,每个参与者可以参加多种行业组织或社团,并参与不同联盟的合作。
在超图(N,H)中,一条长度为k的路(path)是指一个点边交错序列(i1,e1,i2,e2,…,ik,ek,ik+1)。这里i1,i2,…,ik+1表示不同的参与者,e1,e2,…,ek表示不同的超边,且对任意1≤1≤k,{il,il+1}∈el。特别地,如果这条路的始点i1和终点ik+1相同,则称它为圈。在(N,H)中,如果两个点i,j间存在一条路(i=i0,i1,…,ik=j),那么称点i和j点是连通的。如果(N,H)中任意两个点都是连通的,则称(N,H)是连通的。对于任意j∈N,本文令ej表示超图对策(N,H)中任意一条超边,且对于任意的点i,j,…,n∈N,超边ej={i,j,…,n}。对于任意非空集合S⊆N,(S,H(S))称为由联盟S导出的子超图,其中H(S)={e∈H|e⊆S}。对于任意H′⊆H,(N,H′)称为(N,H)的一个部分超图。在(N,H)中,C称为(N,H)的一个分支,即C是一个极大的连通子超图,我们记所有分支的集合为N/H。为了方便起见,对S⊆N,记S/H(S)为S/H。对于任意分支C∈N/H,我们用H(C)表示分支C中超边的集合。
三元组(N,v,H)表示一个超图对策(hypergraph game),它是由一个TU-对策(N,v)和一个超图(N,H)两部分组成。记参与者为N的所有超图对策(N,v,H)的集合为HN。如果对于任意的超图对策(N,v,H)∈HN都有唯一的支付向量F(N,v,H)∈RN,我们称F是超图对策的一个解。在图对策Myerson的值[2,4](Myerson)和Position值(Meessen)的基础上,van den Nouweland等[5]进一步给出了超图对策(N,v,H)∈HN上Myerson值和Position值的定义。Myerson值μ可以表示为:
μ(N,v,H)=Sh(N,vH)
(2)

(3)




(4)

在刻画超图对策上赋权Position值之前,我们先给出一个引理,它是由Borm[3]提出的,它阐述了边对策的一致性系数和联盟对策的一致性系数两者之间的关系。

(5)
2 超图对策的赋权值的刻画
在本小节,我们给出任意超图对策的赋权Position值的公理化刻画。首先,我们给出六个基本性质公理.。第一个性质是经典的分支有效性[4,5]。

分支有效性表示对(N,H)的每一个分支C,分配给该分支中所有参与者的支付之和恰好等于该分支的效用v(C)。

F(N,v,H)=F(N,v,H{e})
Borm[3]定义了冗余边性质:对于任意的边集A⊆L,如果rv(A)=rv(A{i,j}),则称边{i,j}∈L是冗余边。冗余超边性质是对Borm[3]定义的冗余边性质从图到超图的自然推广。
超边可分解性建立在van den Brink[15]提出的边一致性对策基础上。边一致性对策可以看作一个否决情况;为了终止一个提议,边L邻接的两个参与者必须完全同意,满足该性质的边对策为边一致性对策。边L一致性对策的公式为:
我们将边一致性对策推广到超图中,得到超边一致性对策的公式:
在超边一致性对策中,超边可分解性确保超边的效用只能在同一条超边中的参与者之间转移。

(6)



Fi(N,uej,{{ej}})×Fi(N,-uej,{{ej}})
=Fj(N,uej,{{ej}})×Fj(N,-uej,{{ej}})
=…=Fn(N,uej,{{ej}})×Fn(N,-uej,{{ej}})
弱能转换简单来说,当联盟中所有参与者合作获得的效用为正值时,若参与者k获得的支付为Fk;那么当联盟中参与者合作获得的效用为负值时,该参与者k分摊的成为1/Fk。

本文分两步证明了本文的主要结论,即超图对策的赋权Position值是满足上述六个公理的唯一解。第一步,当超图对策为一致性对策时,超图对策的赋权Position值是同时满足分支有效性、拟可加性、冗余超边性、超边可分解性、弱积极性和弱能转换六个性质的解。第二步,我们运用拟可加性证明赋权Position值满足唯一性。然而,如例1所示,存在某些情况不满足拟可加性。
例1假如存在一个超图对策(N,v,H),N={1,2,3,4,5},v=2u{1,4}-3u{1,2,3,4,5},H={{1,2,3},{3,4,5}},那么,r2u{1,4}=∑A∈H0uA+2uH,r-3u{1,2,3,4,5}=∑A∈H0uA-3uH,因此得,λH(r2u{1,4})λH(r-3u{1,2,3,4,5})<0。由拟可加性可知,超图对策(N,2u{1,4},H)和(N,-3u{1,2,3,4,5},H)不可比较。

(7)
对于特征函数ηv,我们有:

(8)

(9)

为了方便接下来的证明,本文又提出两个引理,并给出初步结论。

(10)



(11)

(12)

(13)

根据上式,我们有:




因此,对于任意的边集A⊆H,我们有rχ(A)=0。假设H=Ø,因为TU-对策[1](N,χ)是0-规范的;结合分支有效性,对于任意i∈N,我们有Fi(N,χ,H)=v({i})=0。假设H≠Ø,由于TU-对策[1](N,χ)是0-规范的;结合分支有效性,对于任意的参与者i∈NN(H),Fi(N,χ,H)=0,接下来,考虑对于任意的分支C∈N/H,令|C|>1,我们有:

因为对于任意的边集A⊆H,rχ(A)=0;所以(N,χ,H)是超边一致性对策。结合超边可分解性和分支有效性,我们有:

因为H(C)≠Ø,因此c=0,但这与条件|C|>1矛盾。 因此,对于任意i∈N,Fi(N,χ,H)=0。那么,我们有:F(N,χ+ηv,H)=F(N,χ,H)+F(N,ηv,H)=F(N,ηv,H)。

下面,我们用两个定理对超图对策的赋权Position值进行刻画。



=rv(H(C))=v(c)




第三个等式相等,因为Shapley值满足冗余超边性质。


所以,我们有:

同理,对于任意点i,j,…,n∈N和任意的超边ej={i,j,…,n},及任意的超图对策(N,-uej,{{ej}}),我们有:
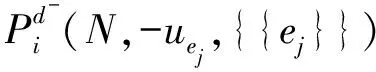


第五,本文可以明显看出赋权Position值满足弱积极性,因此不作证明。


下面我们证明赋权Position值满足唯一性。



(14)
(15)

已知超边对策为超边一致性对策,根据引理2,我们有:






根据式(14),对于任意的超边ej∈Hi,我们有:
(16)


=λS(ηv)uH(S)

3 超图对策举例分析


(17)


4 结论
本文我们研究了参与者的交流能力或合作水平与其在联盟中利润分配或成本分摊之间的关系,定义了超图结构中利润分配或成本分摊的一种方法,使得利润分配或成本分摊更加合理。通过引入超图结构中点的度值来度量每条超边中每个参与者的交流能力或合作水平,并结合Haeringer提出用于推广Shapley值的权重系统定义了一类新的权重系统。根据分支有效性、超边可分解性、冗余超边性、拟可加性、弱能转换以及弱积极性六个性质公理刻画了具有超图合作结构的赋权Position值。我们发现参与者获得的支付随其度值的增加而增加,参与者分摊的成本则随其度值的增加而降低。当然,除考虑用参与者的度来度量其交流能力或合作水平外,还可以用边的度来度量用于交流的每条边的交流容量或者能力,然后研究边的度值对每条边的利润分配或成本分摊的影响,进而研究相应的Position值的公理化刻画问题。

