生物社会网络算法研究

袁 恋,陈 明,刘衍民*

（1.贵州民族大学数据科学与信息工程学院贵州贵阳550025；2.遵义师范学院数学学院贵州遵义563006）

1 引言

近年来，国内外的学者为了解决非线性、全局寻优、组合优化等复杂的优化问题，提出了不少性能良好的群体智能优化算法，例如：粒子群算法、遗传算法、蚁群算法、神经网络算法、模拟退火法等。由于这些算法在图像处理、模式识别、电子通信、自动化控制等众多领域中得到了成功的应用，因此吸引了众多国内外学者的关注，掀起了群体智能优化算法的研究热潮。

在现有的进化算法中大多都难以平衡全局搜索能力与局部搜索能力的问题，如：在粒子群算法（PSO）中[1]，由于其收敛速度快，容易陷入局部最优解，无法对解空间的未知领域进行开发，导致其收敛精度低和不易收敛。在蚁群算法（ACO）[2]中，由于其初始信息匮乏，一般需要较长的搜索时间，导致其容易陷入局部最优，而且CAO在搜索过程中容易出现停滞现象，即在搜索进行到一定程度后，所有个体发现的解完全一致，不能对解空间进一步的进行探索，不利于收敛。遗传算法（GA）[3]具有良好的全局搜索能力，可以快速的搜索出解空间中的全体解，防止其陷入局部最优解的快速下降陷阱，但是GA的局部搜索能力较差，搜索时间长，导致在进化后期的搜索效率较低。模拟退火算法(SA）[4]虽然具有摆脱局部最优的能力，但是SA缺乏对整个搜索空间结构的了解，在搜索过程中难以进入到有希望的搜索区域，不利于寻求最优解。

为了克服传统进化算法难以平衡全局搜索能力与局部搜索能力的问题，本文提出了一种基于生命进化行为的新型生物社会网络优化算法（BNSO）。该算法使用群体搜索技术，通过个体与环境、个体与细胞、个体与个体、个体与群体的交互机制，使种群中的个体相互“协作”和“竞争”，从而产生新的种群，并逐步使种群进化到包含或接近最优解的状态。

2 相关工作

粒子群算法源自于对鸟群捕食行为的研究，在1995年Kennedy和Eberhart提出了粒子群算法。该算法将空间中的每一个鸟都看作是一个轻微粒子，代表问题的一个潜在解，每个粒子初始时都被赋予了飞行的方向和速度。然后结合自己的运动经验并与其它粒子进行共享位置和速度信息来调整自身的飞行方向，直到收敛到全局最优解，一些学者也提出了改进算法[5]-[8]。

蚁群算法是对自然界中蚁群寻求最优路径的研究：蚂蚁在寻找路径的过程当中在途径的路径上释放信息素进行信息传递，而蚂蚁在运动的过程中能够感知这种物质，并以此来引导自己的运动方向。基于这样的群体行为，M.Dorigo和A.Colorni等人通过仿真提出的一种基于种群的启发式随机搜索算法。在搜索过程中的蚂蚁会释放信息素，在碰到还没走过的路口就随机挑选一条路走，同时，释放与路径长度有关的信息素，信息素浓度与路径长度成反比。随着时间的推移，当一条路径上经过的蚂蚁越来越多时，就会留下越来越多的信息素。后来的蚂蚁再次碰到该路口时，就选择信息素浓度较高的路径，最优路径上的信息素浓度越来越大，最终蚁群可通过路径上的信息素浓度找到最优寻食路径，一些学者提出了一些改进的ACO算法[9]-[12]。

遗传算法是由J.H.Holland首次提出，该算法是一类以达尔文进化论和孟德尔遗传学说为理论基础的仿生型算法。GA使用群体搜索技术，将种群代表一组问题的解，通过对当前种群执行选择、交叉、变异等遗传操作来产生一个适合生存的种群，以此来求解出优化问题的全局最优解。

免疫算法[13]是结合基因进化机理，模仿生物免疫机制，从而人工构造出的一种智能优化算法。该算法将生物免疫系统中的抗原视为一个待优化问题，将抗体视为优化问题的可行解，根据待优化问题的特点设计合适的抗体编码规则。并在此规则下利用问题的先验知识产生初始抗体种群，对种群中的抗体质量进行评价，对优秀的抗体进行免疫选择、克隆、变异、克隆抑制等免疫操作，形成基于生物免疫系统克隆选择原理的进化规则和方法，实现对各种问题的寻优搜索。

以上所提到的进化算法，对解决大多的优化问题都具有较好的性能，但都存在难以平衡全局搜索能力与局部搜索能力的问题。

3 生物社会网络算法

3.1 提出生物社会网络算法

美国著名的生物学家Thomas H.Morgan提出“生命=DNA+环境+环境与遗传的交互作用”的思想，生命的进化是个体与个体、个体与细胞、个体与环境、个体与种群的交互作用。

种群中的每个个体通过个体与细胞的交互作用实现遗传物质的变异为种群的进化提供原料；通过个体与环境的交互作用使个体适应不断变化的环境；通过个体与个体的交互进行个体间信息的交流；通过个体与群体的交互来获取有利于进化的遗传信息，选取个体适应度强的遗传信息遗传给下一代，从而实现种群的进化。

图1 生物社会网络的规则

根据ThomasH提出的生命进化思想（如图1所示），我们对个体生命进化行为进行建模与仿真，将个体进化行为置于“细胞→个体→环境→细胞”构成的生物网络与社会网络的结点中，研究个体进化过程，进而提取一种基于生命进化行为的新型生物社会网络优化算法。

3.2 生物社会网络算法的建立

美国著名遗传生物学家Thomas H.Morgan指出目前已知地球上现存的生命主要是以DNA作为遗传物质，除遗传外，决定生物特征的因素还有环境，以及环境与遗传的交互作用。借鉴生命进化的过程，对生命进化过程进行建模。首先将“细胞→个体→环境→细胞”看作生物网络与社会网络的混合体，这里称作“生物社会网络”，将个体看作生物社会网络中的一个结点，细胞自身形成细胞周期网络，环境看作个体所处的社会群体，它会对个体产生宏观（自身适应能力的改变）和微观（基因突变、基因重组等）的影响。

基于生命进化行为基础上，我们利用BA无标度网络来作为生物社会网络的基础，将个体看作生物社会网络中的一个结点，细胞自身形成细胞周期网络，环境看作个体所处的社会群体，它会对个体产生宏观（自身适应能力的改变）和微观（基因突变、基因重组等）的影响。采用BA无边度网络对种群个体影响过程如下：

(2)优先连接：一个新的节点与一个已经存在的节点 相连的概率与节点 的度之间的关系为=/(+++…+)，其中为网络中的节点的总个数。

(3)节点决策：给出每一个节点的概率分布，作用是通过产生0(1之间的随机数来做出决策。

(4)通过节点决策概率，选择新增进入的个体。选择过程根据环境的变化优先选择。

图2给出基于不同种群规模的度分布图。可以看出，当节点初始规模为种群规模的60%时效果最佳，因此，在本文提出的算法中，采用种群规模的60%作为初始增长节点。

3.3 生物社会网络算法过程

图2 种群BA网络度分布图

生命进化行为建模具体包括：生物社会网络中细胞、个体和环境之间的复杂相互作用，它类似于生命体中个体与细胞的交互，完成基因的突变、染色体的变异、基因的重组。个体所在细胞周期网络的突变对个体成长的影响类似于种群中的个体通过结合个体与个体间的交流信息和个体与群体的交流信息的过程。具体如下：

假设由N个个体组成一个种群，每个个体携带了D个基因。将D维决策空间中的第i个个体表示为：

第i个个体根据公式（2）实现个体与环境的交互，使进化的个体能够适应不断变化的外部环境。

第i个个体根据公式(3)(4)(5)实现个体与细胞的交互，完成基因的突变、染色体的变异、基因的重组，给个体的进化提供原料。

种群中的个体根据公式（6）进行个体间的信息交流。

这里C1是［0，1］范围内的均匀随机数；是到第n次迭代为止，第i个个体的最优个体;代表个体通过与个体间交流所获得的遗传信息.

种群中的个体根据公式（7）获取有利于种群进化的遗传信息.

这里C2是［0，1］范围内的均匀随机数;是到第n次迭代为止，种群中的最优个体;是个体通过与群体间交流所获得的有利于种群进化的遗传信息.

种群中的个体通过结合个体与个体间的交流信息和个体与群体的交流信息，根据公式（8）实现进化。

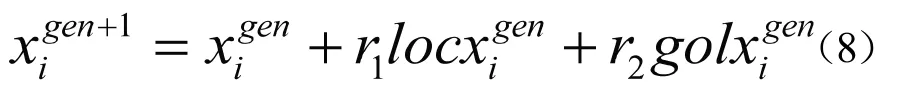
这里r1r2是［0，1］范围内的均匀随机数。

3.4 生物社会网络算法流程

生物社会网络算法使用群体搜索技术，通过个体与环境、个体与细胞、个体与个体、个体与群体的交互机制，使种群中的个体相互“协作”和“竞争”，从而产生新的种群，并逐步使种群进化到包含或接近最优解的状态。

生物社会网络算法（BNSO）的流程如图3所示。具体的步骤如下：

步骤1：初始化。包括种群规模N，随机生成初始化种群P。

步骤2：计算每个个体的适应值.

步骤3：执行个体与环境的交互机制.对种群中的个体以一定的概率进行扰动操作，产生新的个体，运行无标度BA网络。

步骤4：执行个体与细胞的交互机制。对种群中的个体执行突变、变异、重组一系列的操作产生新的个体。

步骤5：执行个体与个体的交互机制，获取个体间交流的遗传信息 。

步骤6：执行个体与群体的交互机制，获取种群中有利于进化的遗传信息 。

步骤7：进化。通过结合个体与个体间的交流信息和个体与群体的交流信息实现进化。

步骤8：判断是否满足终止条件：若是，结束算法并输出结果；否则，返回步骤2.

图3 BNSO流程图

4 实验仿真及其分析

为了测试BNSO算法，我们采用了11个Benchmark函数[14]来测试提出算法的性能。并且将BNSO算法分别与GPSO,LPSO,GA和AOC算法相比，来检测我们提出算法的有效性。另外，为进一步测试算法的性能，将检测函数进行旋转，以进一步测试BNSO算法的优化能力，旋转方法参见文献[15]，表1和表2分别给出旋转检测函数和非旋转检测函数的函数属性。各种算法参数设置如下：PSO种群规模为30个粒子，检测函数独立运行30次取平均值，每个检测函数的维数为30，其它参数的选取与算法提出时一致。另外，对非旋转和旋转的检测函数每次运行3×104函数评价(Fitness Evaluations)。

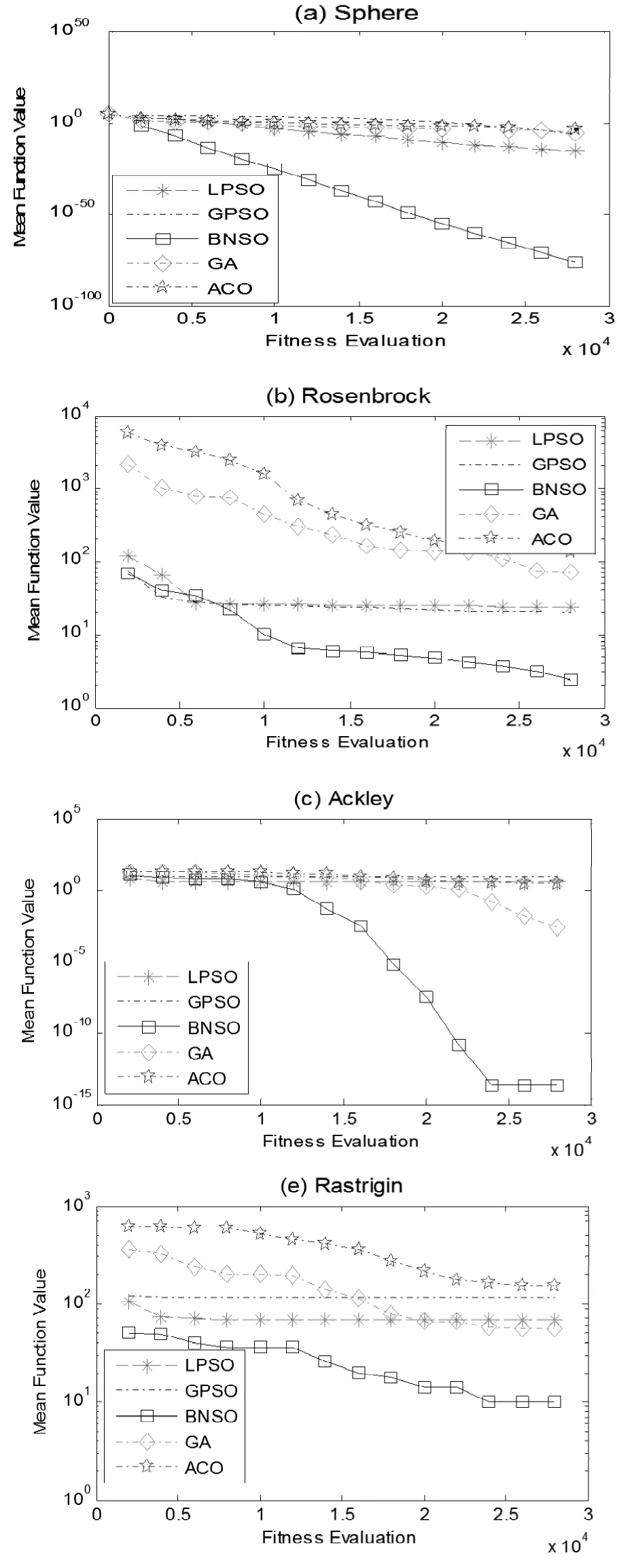
图4 非旋转检测函数收敛图

图5 旋转检测函数收敛图

表1 非旋转的Benchmark函数

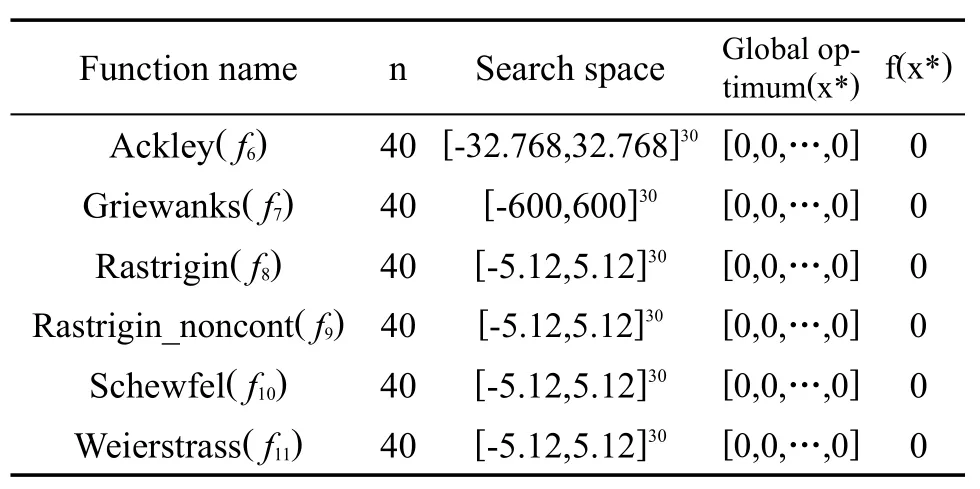
表2 旋转的Benchmark函数

图4和图5分别给出不同算法在旋转检测函数和非旋转检测函数的收敛特征曲线图。表3和表4分别给出非旋转函数和旋转检测函数在3×104函数评价后的均值和置信区间，为检验BNSO优化能力与PSO，ACO,GA算法在优化能力上是否具有统计学差异，用Wilcoxon秩和检验来测试BNSO与其它算法的优化结果进行检测，统计结果在表3和表4的底部。

另外，为测试不同算法的计算复杂度，采用用Matlab 2013软件中的(tic,toc)命令来测试算法运行时间，表 5和表 6分别给出非旋转检测函数在 3(104FES函数评价后的运行时间。

从图4和图5非检测函数和检测收敛图中可以看出BNSO算法在收敛特性中优于其它三种智能算法。表3和表4的运行结果统计图也显示出同样的结果。但是，在对于单峰检测函数Sphere来说，虽然BNSO优于GA、LPSO、GPSO和GA算法，但是在 Wilcoxon秩和检验检测中并没有在统计学意义下优于其它算法，这也说明智能算法在优化单峰问题时都具有较好的效果。但是BNSO算法在多峰检测函数和旋转的多峰检测函数上表现出了极优的运行效果，这也说明本文提出的借鉴“生命=DNA+环境+环境与遗传的交互作用”的思想，提出的生物社会网络算法能有效的优化单目标问题。另外，从计算复杂度上也可以看出BNSO算法虽然有较好的优化效果，但计算复杂度并没有增加。

表3 非旋转函数在3×104函数评价后的均值和置信区间

表4旋转函数在3×104函数评价后的均值和置信区间

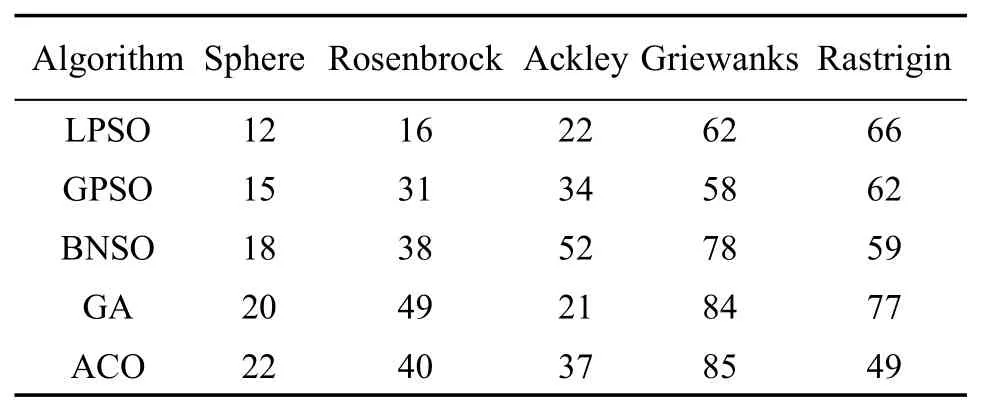
表5非旋转检测函数计算时间3×104FES)(单位:秒)

5 结论

为了解决传统进化算法难以平衡全局搜索能力与局部搜索能力的问题，本文提出一种具有生命演化和群体智能的生物社会网络优化算法（BNSO）。为了测试BNSO算法性能，我们选取11个单峰和多峰检测函数来测试算法性能，结果表明BNSO优化能力优于PSO,ACO,GA算法。尤其BNSO算法在多峰检测函数和旋转的多峰检测函数上表现出了极优的运行效果。因此，本文借鉴“生命=DNA+环境+环境与遗传的交互作用”的思想，提出的生物社会网络算法是解决单目标优化问题的一种有效算法。