基于黏度计读值预测的高温高压流变性预测方法

周号博

（中国石化石油工程技术研究院，北京 100101）

0 引言

随着中国油气资源的勘探开发逐步向深部地层进军，高温高压深井、超深井的数量逐年增加，中石化西北油田顺南、顺北地区及中石油塔里木油田克深、大北地区的油气资源普遍埋深大于7000 m，部分油气井钻探深度达8000 m[1]。对浅部地层钻井而言，温度、压力对钻井液流变性影响不大，但在深部地层，温度、压力综合作用对钻井液流变性影响较大。对井筒钻井液的流变性进行准确分析是钻井参数优化设计、井筒压力分析的基础。因此有必要进行高温高压对钻井液流变特性的影响评价与分析，建立井筒高温高压流变参数预测模型，为钻井优化设计、井筒压力计算、钻井液性能调整等提供理论依据。

为了能够准确地计算钻井水力参数，上世纪50年代国外开始了高温高压钻井液流变性研究，但主要集中在宾汉塑性模型及幂律假塑性模型上，没有形成系统的高温高压流变参数计算方法。1958年， Srini-vasan和Gatlin运用Fann V-G黏度计对黏土水基钻井液在不同温度下的流变性进行了分析，给出了简单的钻井液塑性黏度预测模型[2]。1967年，Annis运用Fann氏高温高压黏度计对水基钻井液高温高压流变性进行了实验研究，给出了高温高压下钻井液屈服值、 黏度变化的定性分析[3]。1975年，McMordie等人基于幂律模型对油基钻井液高温高压流变性进行了相关研究，其在分析过程中将幂律模型两边取对数转化为线性模型，同时假定温度压力只对钻井液稠度系数产生影响，对流性指数没有影响， 进而给出了简单的稠度系数预测模型[4]。1985年，Politte[5]采用宾汉模型对高温高压下逆乳化油基钻井液流变性进行了实验分析， 并给出了宾汉屈服值及塑性黏度的预测模型。其后有许多研究人员进行了相应的钻井液高温高压流变性研究与分析，但大多基于American Petroleum Institute（API）推荐的宾汉、 幂律流变模型， 通过流变实验回归得到相应的流变模型流变参数回归模型[6-7]。自20世纪80年代末以来，中国学者开始逐渐对高温高压下钻井液性能进行研究，得到了相应的高温高压流变参数预测模型。1989年，鄢捷年对不同密度的矿物油基钻井液和常规油包水乳化钻井液高温高压流变性进行了实验分析，主要分析了不同温度压力下钻井液塑性黏度、表观黏度、屈服值随温度和压力的变化情况[8]。1990年， 鄢捷年给出了油包水乳化钻井液表观黏度的预测模型[9]。2009年， 赵胜英等对该模型做了改进，进一步提出了预测塑性黏度、屈服值、表观黏度的综合[10]。同年，赵怀珍等进行了抗高温水基钻井液超高温高压流变性实验研究，经过实验给出了钻井液表观黏度预测的数学模型[11]。除上述列举的高温高压流变性分析外，中国其他学者也做过高温高压钻井液流变性分析与评价[12-14]。

综上，钻井液高温高压流变性分析多基于宾汉、幂律模型进行，通过实验给出的流变参数预测模型多为经验公式。该方法首先假定了流变模型，然后引入变量温度T和压力P，修正计算高温高压流变参数。这些模型均建立在高温高压流变参数与温度、压力（或温度、压力变化量）经验公式的基础上，即通过实验数据拟合经验公式进而预测某一钻井液在不同温度、压力下的特定流变参数（如塑性黏度、表观黏度等）。该方法存在如下不足：其一，由于其建立的是特定流变参数与温度、压力（或温度、压力变化量）经验公式，即导致了经验模型具有一定局限性，不能适用于所有流变模型，特别是随着深井、超深井普遍增多，钻井液也越来越复杂，因此很难用一种流变模型描述所有流体的流变特性[15]；其二，由于其建立的是流变参数与温度、压力的经验公式，倘若在建立经验模型之初所计算的不同温度压力下流变参数存在误差，则可能引起经验模型的不准确。因此，需要从对钻井液流变性分析的基础出发，建立一种通用的高温高压流变分析方法。

1 高温高压流变实验

钻井液流变性是通过测量旋转黏度计不同转速下的读值，对不同转速下读值进行计算分析后优选流变模型，进而得到流变参数，为钻井水力参数计算提供基础参数。由此可知，钻井液流变性分析的基础是获取准确的黏度计读数，如果能够对高温高压黏度计读值进行准确预测，即可解决高温高压流变分析问题。

为了分析高温高压下黏度计读值的变化规律，采用安东帕高温高压流变仪在不同温度（20～180 ℃）、不同压力（0～6 MPa）下，对1#钻井液进行了高温高压流变实验，高温高压黏度计实测结果如表1所示。根据表1给出的高温高压黏度计读值结果，分别绘制了6 MPa、不同转速下不同温度时黏度计读数及60 ℃时不同转速下不同压力的黏度计读数变化曲线图，如图1、图2所示。

表1 1#钻井液高温高压黏度计实测结果

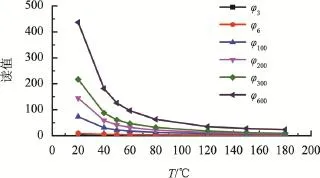
图1 黏度计读值在6 MPa下不同温度下的变化曲线

由图1可知，在压力不变的条件下，黏度计读值受温度影响很大，在温度较低时，黏度计读值随温度升高呈现急速下降趋势，当温度达到120 ℃以后，黏度计读值随温度变化不明显，下降趋势逐渐趋缓。

图2 黏度计读值在60 ℃时不同压力下的变化曲线

由图2可以看出，在温度保持不变的情况下，黏度计读值随压力升高呈线性上升，不同转速下曲线斜率不同，同时可见黏度计读值受压力影响程度较温度影响程度低。

2 钻井液高温高压流变性预测模型

由于流变参数是基于旋转黏度计不同转速下测量的一组读值计算得到，只要建立对应转速黏度计读值在不同温度、压力下的预测模型，即可根据黏度计读值分析钻井液高温高压流变性，可以从根本上解决高温高压流变模型优选与计算的难题。

设初始温度为T0、初始压力为P0时测得的黏度计读值为θ0，0，则对于转速RPM、温度Tk、压力Pj时黏度计读值θj，k可表示为如下方程：

式中，θΔPj，ΔTk表示转速 RPM 下温度 Tk、压力Pj所对应的读值，无因次 ；ζj，k表示 θΔPj，ΔTk与θ0，0的比例因子，无因次 ；ΔPj表示压力变化量，ΔPj=Pj-P0，MPa；ΔTk表示温度变化量，ΔTk=Tk-T0，℃。

2.1 比例系数与温度关系

为分析 θ0，0与 θj，k之间的关系，以表 1 中 600转黏度计读值为例，以20 ℃、0 MPa测量结果作为 600 转黏度计读值基值，即 θ0，0=387.5。由图 1（b）已知，在温度不变情况下、黏度计读值随压力升高而线性增大。因此，根据表1数据对常压下600转黏度计读值在120 ℃、150 ℃时的结果进行了线性预测，得 θ600，0，120℃=34.8、θ600，0，150℃=27.6。则可得ζj，k如表2所示。由表2可知，比例因子ζj，k不是常数，其随ΔT、ΔP变化而变化，因此可将比例因子表示为ΔT、ΔP的函数，即ζj，k=f（ΔTk、 ΔPj），只要建立比例因子ζj，k与温度差、压力差的表达式，即可获得不同温度压力下的黏度计读值，从而对钻井液高温高压流变参数进行预测。

在对生态城市进行建设的过程中，城市经常会产生较多生活垃圾、工业废料，这些固体废弃物会对人们的生活环境产生很大影响。因此可以成立垃圾处理系统，设置城市中的垃圾分类处理试点，加强垃圾的分类与回收效率。还应不断完善与优化固体废弃物回收循环再利用系统，将环境保护、节约资源的理念作为基础，提升城市的整体经济效益与生态效益，减少资源损耗，最终达成生态城市的建设目标。

表2 黏度计600转读值比例因子ζj，k计算结果

根据表2可将比例因子、温度变化、压力变化采用如下矩阵表示：

式中， ζi表示黏度计转速 i时的比例因子矩阵， 无因次 ；j=0， 1， …， j，表示测量了 j+1 个压力下高温高压流变实验， 无因次 ；k=0， 1， …， k， 表示测量了k+1个温度下的高温高压流变实验， 无因次。

首先，以表2所得的比例因子ζ600为例，分析了初始压力 P0时向量 ζ0，k=（ζ0，0，ζ0，1，…，ζ0，k）随温度变化关系，拟合得如下方程：

由式（3）可知，ζ0，k可以表示成自然常数e的关于温度差ΔT的指数方程，根据式（3）绘制了 ζ0，k预测值如图 3 所示。

图 3 比例系数 ζ0， k结果对比

由图3可以看出，预测结果与实测点吻合很好，且能很好地展现出其变化趋势。同时，对不同压力差情况下的比例系数矩阵ζi其余行向量随温度差的变化进行了分析，也可用如式（3）的指数方程表示。因此，对于压力不变情况下，比例因子可以表示为如下方程：

式中，ΔTk从温度变化向量ΔT中取值，根据公式（4）可表示压力不变情况下的黏度计读值随温度变化趋势。

2.2 比例系数与压力的关系

前面分析了比例因子与温度变化关系，得到了压力恒定情况下比例因子的预测方程。为了很好地描述比例因子与压力变化的关系，首先运用式（4）对ζi矩阵的各行向量进行计算分析，可得600转比例因子完整矩阵，即 ζ0，7=0.0606、ζ1，7=0.0611、ζ2，7=0.0616。前已述及，温度不变、压力变化时，黏度计读值与压力变化呈线性关系，因此比例系数矩阵ζi的列向量也呈线性增加趋势。即可将比例系数各列向量表示为：

式中，ΔPj从压力变化向量ΔP中取值，基于式（5）根据表2及预测分析的矩阵数据，可得系数d、f如表3所示。

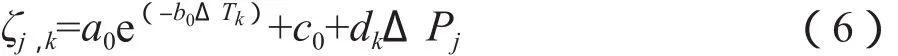
式中， a0、 b0、 c0表示为当压力为初始压力时所得式（4）的比例系数。

通过式（7）即可求取不同温度压力下黏度计读值的比例系数，由表3可知，系数d是随温度变化而变化，同样可根据其变化规律将其拟合得到如下方程：

根据式（7），同样可将系数d表示为如下指数形式，即：

表3 黏度计600转读值比例因子ζj列向量系数计算结果

2.3 高温高压黏度计读值预测方法

合并式（2）、式（6）及式（8）即可得黏度计读值的通用预测模型，可表示为如下方程：

式中， A=a0θ0，0、 B=b0、 C=c0θ0，0、 D=gθ0，0、 E=h、F=mθ0，0。

通过式（9）即可得旋转黏度计各转速下读值的通用预测模型，它是温度差ΔT和压力差ΔP的函数，该式综合考虑了温度及压力变化对黏度计读值的影响。

图4给出了基于式（9）进行高温高压流变性分析的流程图。对于某一体系钻井液，只要有一组高温高压流变性实验数据，即可根据式（9）得到黏度计各转速下读值变化规律，进而分析得到井筒中不同位置时黏度计读值。基于预测的黏度计读值，可以进行流变模型选择与流变参数计算，这样使得该模型不再局限于常规的宾汉、幂律模型等特定流变参数的预测，使该方法具有普适性。

3 模型验证与应用分析

为了验证该方法的准确性，首先根据式（9）及图4所示计算流程，计算得到了1#钻井液的高温高压黏度计读值预测模型系数，如表4所示。根据表4所得模型系数，预测了1#钻井液0 MPa及4 MPa不同转速时的黏度计读值，见表5。

比较不同温度和压力下的预测和测量黏度计读值，可以看出预测的最大绝对误差小于5，相对误差仅为2%。

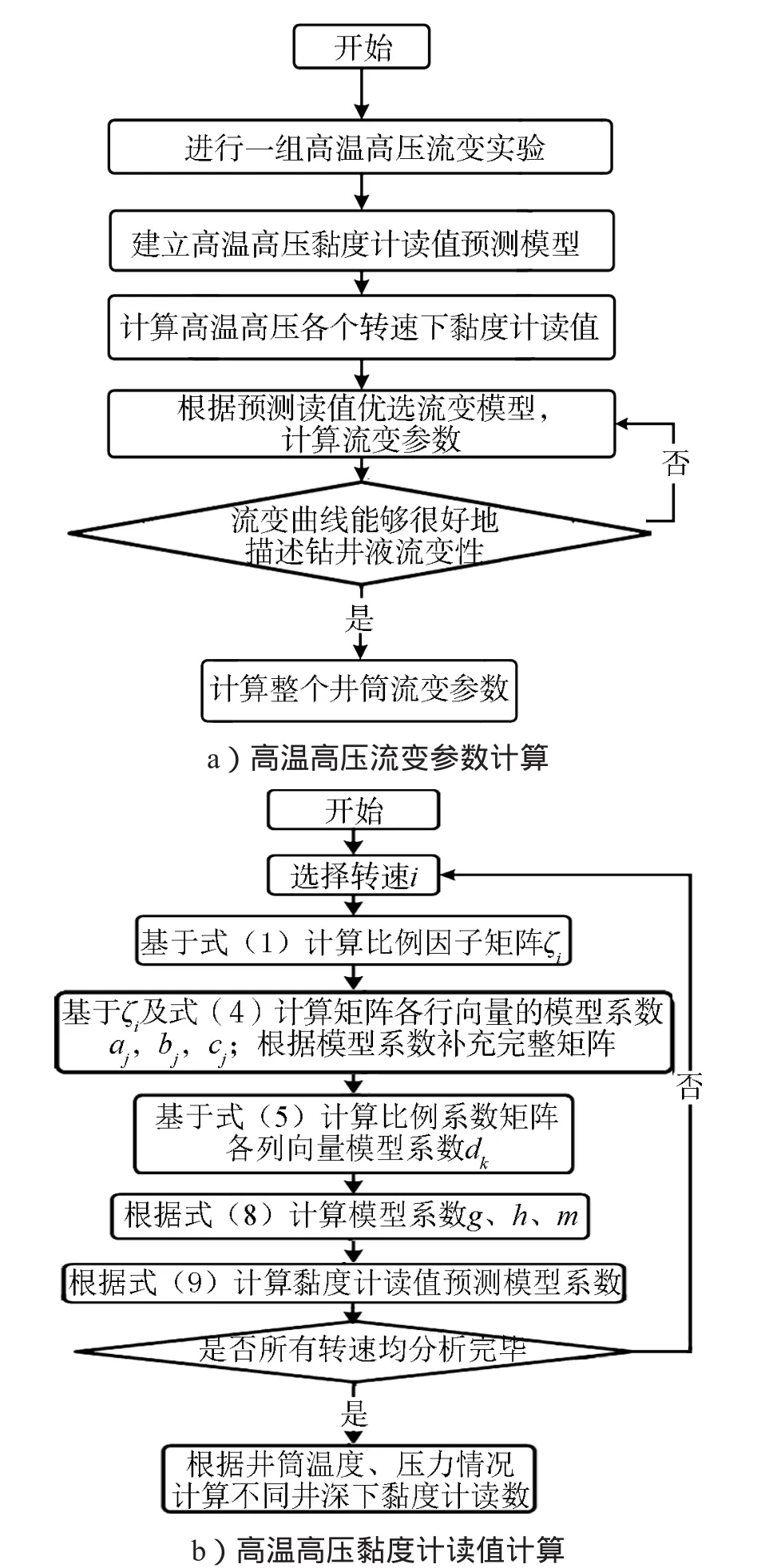
图4 高温高压流变参数预测流程图

此外，可以看到该流变实验中常压最高温度为80 ℃，但基于预测模型，可以很容易地预测出较高温度下的黏度计读值。类似地，根据该预测模型，也可以容易地获得高于测试压力的压力下的黏度计读值。因此，该模型能够准确预测不同温度和压力下黏度计高温高压流变实验黏度计读值，为预测高温高压流变性能提供准确的基础数据。然后，根据预测的黏度计读值分析和选择最佳流变模型来描述钻井液流变性。

表4 1#钻井液黏度计读值预测模型系数

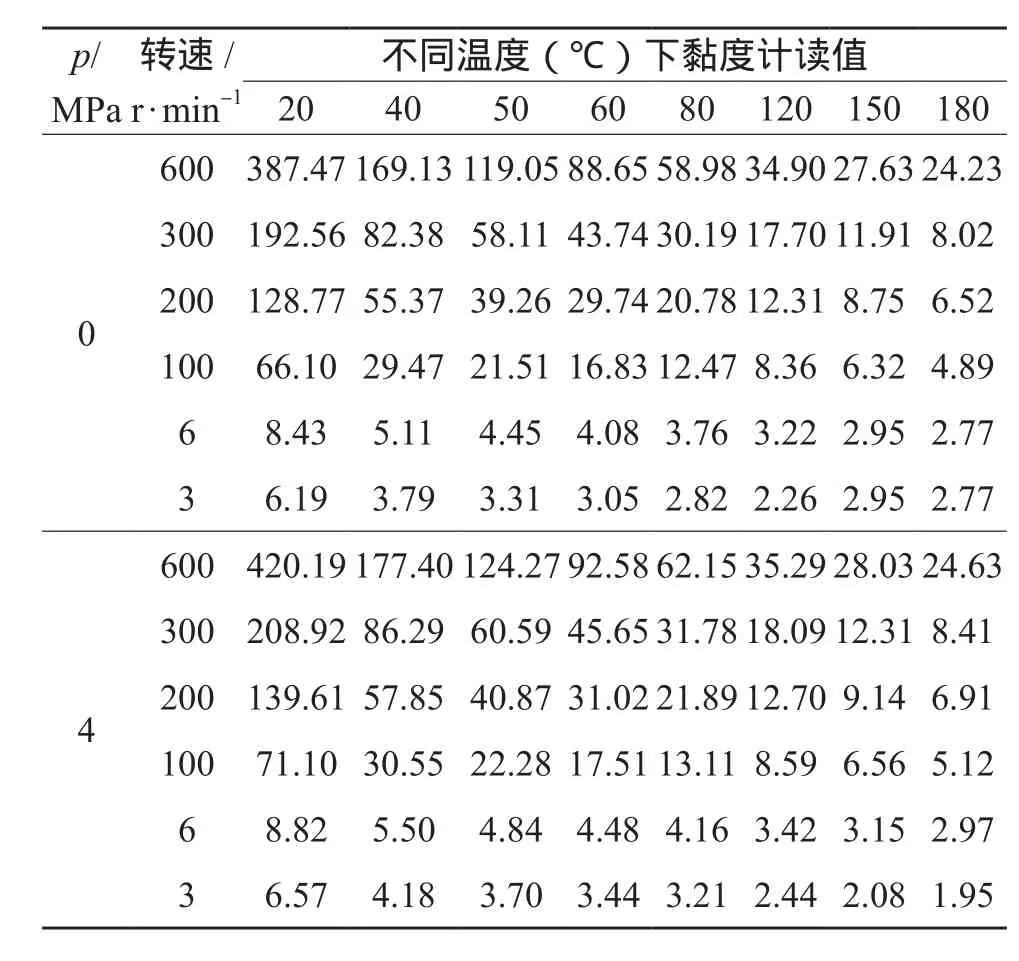
表5 1#钻井液不同温度下黏度计读值预测结果

此外，为了验证所提出的模型的适用性，采用Fann75黏度计对某井现场用钻井液（2#钻井液）进行了高温高压实验，实验结果如表6所示。

表6 2#钻井液高温高压黏度计实测结果

基于高温高压实验结果，计算了2#钻井液高温高压黏度计读值预测模型系数并列于表7中。

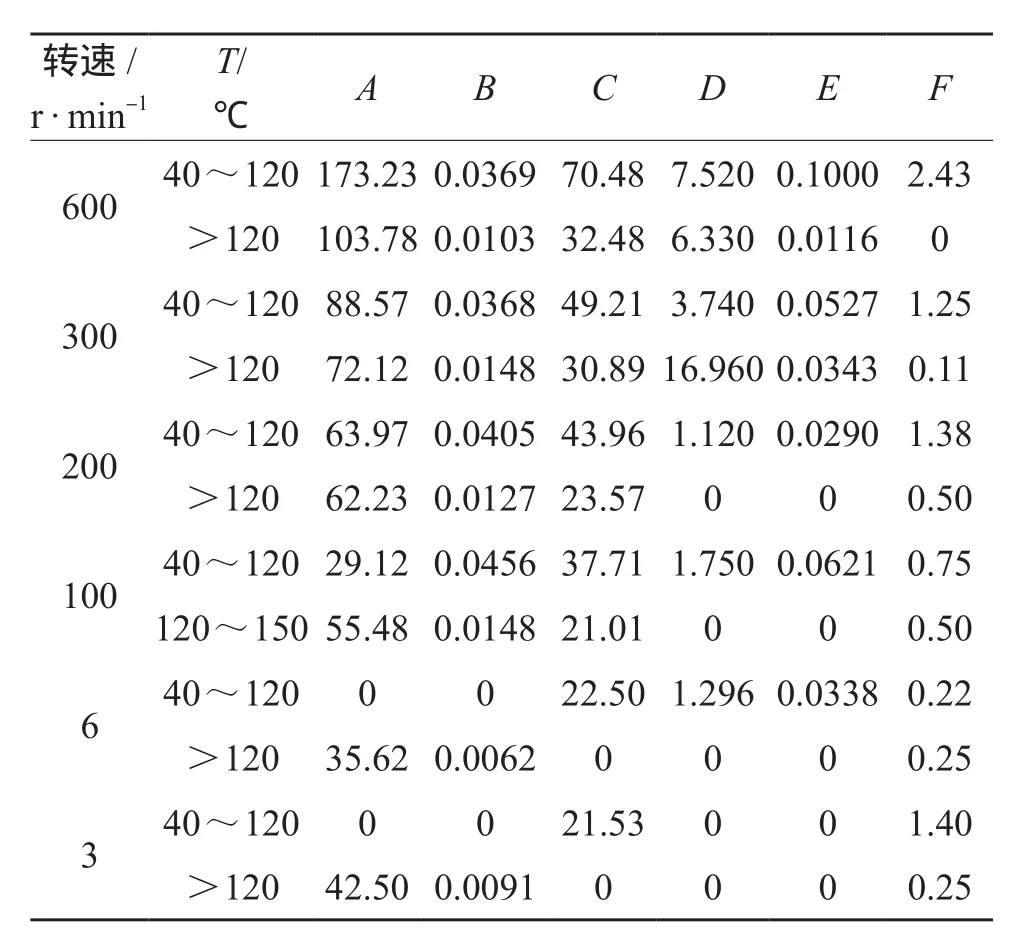
表7 2#钻井液黏度计读值预测模型系数

根据模型系数，可以很容易地获得该钻井液在不同转速下的高温高压黏度计读值。运用该预测模型预测了8 MPa下黏度计读值在表7给出，对比表6实测数据可以看出，预测结果与实验结果具有极好的一致性。在其他压力下也获得了同样高的预测精度，在其他压力下黏度计读值的预测也获得了高精度。

表8 2#钻井液黏度计读值预测结果

图5和图6给出了预测和测量数据计算所得的流变曲线，可以看出，该钻井液为屈服假塑性流体，选择了卡森模型描述该钻井液流变特性，拟合所得曲线能够很好地描述钻井液的流变性。

2#钻井液应用井位于塔里木盆地X区块， 深度为6736 m， 是一个重要的勘探井，井底温度高于150 ℃。 根据表7中列出的该钻井液的黏度计读值预测系数可以容易地获得钻井时井中钻井液的流变参数。在此使用Raymond[16]提出的模型来计算环空中的温度分布，并且可以基于Harris和Osisanya提出的模型来计算井筒压力[17]，最终计算所得该钻井液在井筒中的流变参数曲线，如图5～图7所示。可以看出，流变参数是与井深有关的变量，而不再是一个常数。在这种情况下，该钻井液的Casson黏度和屈服应力随着井深的增加而增加。屈服应力值与地面测量结果相比增加了近50%，井底处的Casson黏度比地面测量结果增大近3倍。

图5 不同温压下钻井液流变曲线（4 MPa、40 ℃）

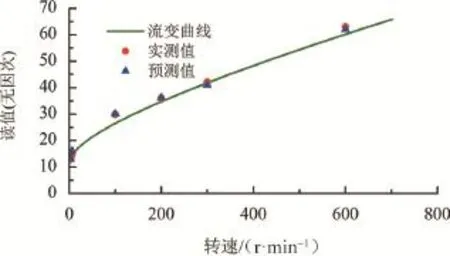
图6 不同温压下钻井液流变曲线（8 MPa、180 ℃）

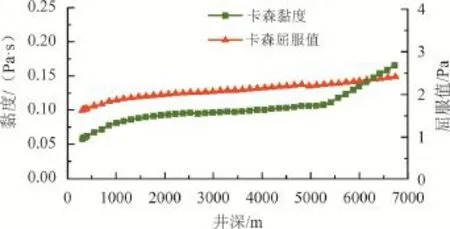
图7 井筒内流变参数变化曲线

为了确保高质量和快速钻井，根据高温高压流变特性预测，可以研究井眼中的钻井液特性并实时调整其流动特性。此外，准确预测流变参数对钻井水力参数计算至关重要，考虑高温高压流变参数变化的水力计算结果比基于地面测量的流变参数计算所得的结果将更为准确。

4 结论

1.基于高温高压流变实验数据，系统地分析了各转速下旋转黏度计读值随温度、压力的变化关系，随后建立了系统的高温高压黏度计读值预测模型，将温度压力与黏度值读值建立了直接联系。

2.通过黏度计读值预测模型，可以计算出不同温度、压力时各转速的黏度计读值，并将其与高温高压流变参数直接关联。由于高温高压旋转黏度计读值预测模型与特定流变参数（塑性黏度、表观黏度等）没有直接关系，因此该方法可以扩展到所有的流变模型。

3.该模型将为钻井工程中一些复杂但更为精确的流变模型在高温高压深井中的应用奠定基础。通过多组实验数据对比分析，该模型可以准确地对高温高压旋转黏度计读值及高温高压流变参数进行预测，证明了该方法的普适性。