单相受热管集总参数模型优化及现代控制工程应用

蔡雨晴，杨平，沈丛奇，康英伟，归一数，徐春梅

(1.上海电力大学 自动化工程学院，上海 200090； 2.上海明华电力技术工程有限公司，上海 200090)

0 引言

目前，针对系统建模的方法有试验建模和机理建模两大类。随着各种智能算法的出现，试验建模法在火电厂热工控制领域取得了很大的进展[1-7]。但事实上，只靠试验方法建模的众多工程实践案例表明：即便拥有非常庞大的数据，也解决不了建模的盲目性问题。例如，模型结构的确定问题，若只靠数据的数学方法分析计算将有多种可选结果，数据拟合最优的结果未必是所需要的正确结果，因为假定的模型结构很可能与实际物理模型完全不吻合。再比如，模型参数范围的确定问题，如果只靠数学方法任意优选，很可能获得的最优模型参数值没有实际意义。因此，依据机理分析方法建立的系统模型在现代控制工程的建模应用中仍有研究价值，可以更科学地确定模型结构和模型参数范围。

集总参数法以其建模简单、计算方便的应用优势，一直广受学者们的关注。早在1962年，Mark E就已经给出了多种假定条件下的单相受热管的集总参数模型[8]。1965年，Adam J等通过仿真验证了单相受热管集总参数模型可以高度可靠地模拟直流锅炉单相区段动态特性的结论[9]。1987年，章臣樾的专著《锅炉动态特性及其数学模型》出版，较系统地陈述了通过机理分析方法建立集总参数模型的过程[10]。1989年，王广军等引入金属当量质量概念，对锅炉动态模型中的能量平衡方程进行修正[11]，得到了改进型集总参数模型。1993年，王泽宁等发现改进型模型并不能达到提高模型精度的目的，某些情况下反而增大了模型的动态误差[12]。2000年，范永胜为了提高单相受热管集总参数模型的精度，通过惯性补偿的方法对该模型进行了动态修正[13-14]。纵观近40年单相受热管集总参数模型的研究历史，可以发现广大学者们一直致力于提高集总参数模型的精度，但到目前为止，一套完整的符合现代控制工程应用的单相受热管的集中参数模型仍未被提出。因此，本课题的目的是建立一个能满足实际控制工程需要的数学模型。

在实际控制工程应用中，模型的实用性应受到最大的关注。本文将建立一个简单实用的集总参数模型，该模型立足于现代控制工程的实际应用，解决目前存在的一些问题，如过程控制量与模型输入量的换算问题、温度测量传感器的惯性问题等，在不增加模型复杂度的基础上提高集总参数模型的精度，进而实现该模型的推广应用。下面将详述该模型，并以1 000 t/h直流锅炉过热器为例建立集总参数模型，最后会将集总参数模型的仿真结果与分布参数模型的仿真结果进行比较。

1 单相受热管集总参数模型

根据文献[10]，选定出口参数作为集总点，则表示单相受热管集总参数模型的微分方程式如下。

连续性方程

(1)

热平衡方程

(2)

内壁传热方程

(3)

金属蓄热方程

(4)

式中：qm为工质流量；V为区段总容积；ρ为工质密度；τ为时间；Q为热流量；h为工质比焓；K2为系数；n为指数，通常取0.8；t为温度；mj为金属总质量；cj为金属比热容；下角标0为稳态值，1为入口侧或外壁面，2为出口侧或内壁面，j为金属。

将式(1)—(4)进行线性化处理，即用变量的稳态值加上其对稳态值的增量来替换变量，然后泰勒展开，略去展开式中增量的高次项，最后对时间变量进行拉式变换整理，得到式(5)。

根据式(5)，可将单相受热管的集总参数模型表示为更便于应用的形式，见式(6)—(9)。

式(5)—(9)中：μ为介质密度随温度的变化率，即μ=∂ρ/∂t；cp为工质定压热容；td为稳态时壁温与出口的温度差，td=tj0-t20；Δt2为出口温度的变化量，Δt2=t2-t20；Δt1为入口温度的变化量，Δt1=t1-t10；Δqm1为入口流量的变化量，Δqm1=qm1-qm0；ΔQ1为热流量的变化量，ΔQ1=Q1-Q0。

(5)

Δt2(s)=Gt(s)Δt1(s)+Gqm(s)Δqm1(s)+GQ(s)ΔQ1(s) ，

(6)

(7)

(8)

(9)

由此可见，该模型有3个输入和1个输出，如图1所示。

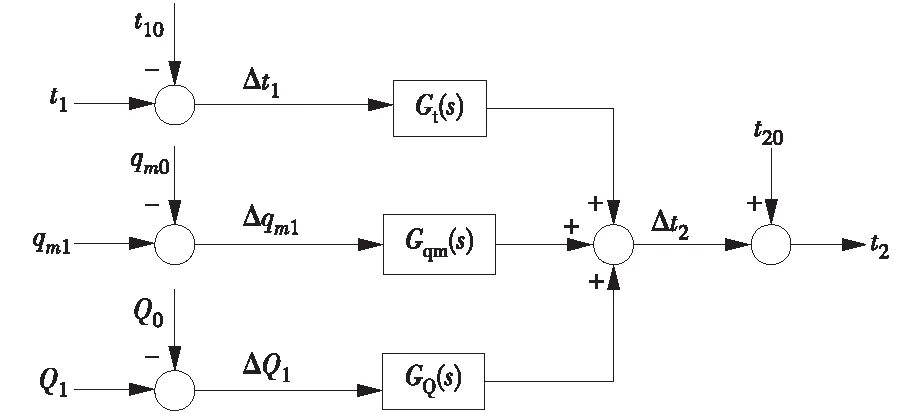
图1 单相受热管集总参数模型Fig.1 Lumped parameter model of single-phase heat pipe

2 单相受热管集总参数模型工程应用问题与解决方法

2.1 过程控制量与模型输入量之间的转换(以喷水减温流量为例)

单相受热管的集总参数模型的输入变量并不一定是过程控制的可自动或人工操作的变量，例如，可通过操作喷水减温流量来调节过热器出口的汽温，这个喷水减温流量并不是单相受热管的集总参数模型的输入变量，因此，若将单相受热管的集总参数模型用于过热汽温喷水减温控制工程，则首先要解决过程控制量与模型输入量之间的转换问题。类似的情况还出现在应用单相受热管的集总参数模型研究通过挡板调节再热器汽温控制的时候。下面以喷水减温流量为例，探讨这类问题的解决方法。

图2给出了喷水减温器与过热器相连的系统分析简图。由图2可知，过热器入口工质流量为喷水减温器入口汽量和喷水减温水量之和。根据文献[15]，可引入过热器入口段温度变化与喷水减温器入口段温度变化之间的关系，即考虑

qm0=qmw0+qm0′ ，

(10)

(11)

式中：qmw0为喷水减温水量；qm0′为喷水减温器入口蒸汽流量；qm0为过热器入口工质流量；Δt1′为喷水减温器入口蒸汽温度的变化量；Kt为喷水减温器出口蒸汽温度与喷水减温器入口蒸汽温度的比值。

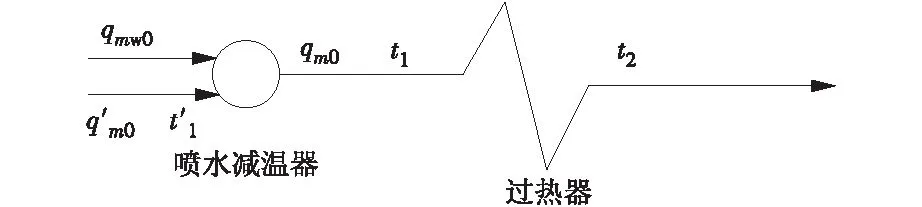
图2 喷水减温器与过热器相连的系统分析简图Fig.2 Analysis diagram of the connection system of water spray desuperheater and superheater

根据文献[16]，若忽略喷水减温器的动态特性，则可引入喷水流量扰动对喷水点后、过热器入口段温度变化的稳态特性关系

(12)

则可得到更便于应用的形式

Δt1(s)=KwΔqmw(s)+KtΔt1′(s) ，

(13)

式中：Δqmw为喷水减温器入口减温水流量的变化量；Kw为喷水减温器出口蒸汽温度与减温水流量的比值。

将式(13)代入式(6)，则可得到用于过热汽温喷水减温控制工程的单相受热管的集总参数模型

Δt2(s)=[KwΔqmw(s)+KtΔt1′(s)]Gt(s)+

Gqm(s)Δqm1(s)+GQ(s)ΔQ1(s) 。

(14)

可见，带喷水量的单相受热管分布参数模型的标幺值模型将有4个输入和1个输出，如图3所示。

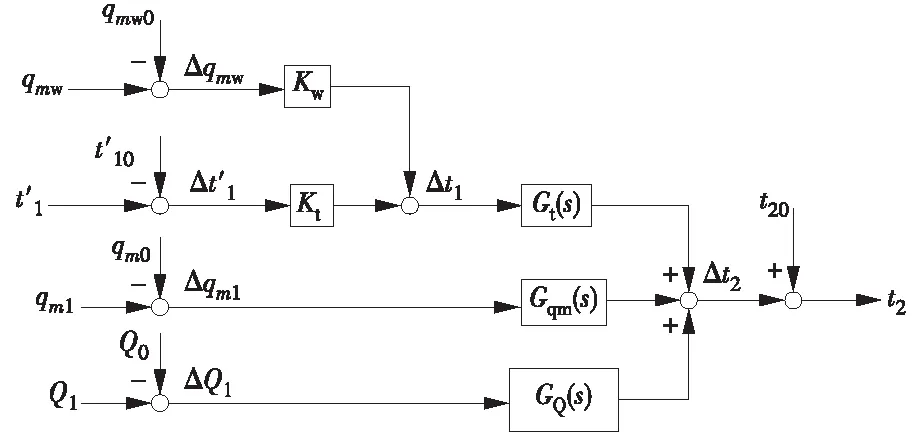
图3 带喷水量的单相受热管集总参数模型Fig.3 Lumped parameter model of single-phase heat pipe with water spray

这样，用于过热汽温喷水减温控制工程的单相受热管的集总参数模型就建立完毕了。

顺便指出，上述针对喷水减温器的建模还不够精确，因为只考虑了喷水减温器的稳态特性，而没有考虑其动态特性。更详细的建模可参考文献[16]。

2.2 温度测量传感器的动态特性模型附加

热电偶是一种结构简单、性能稳定、测温范围宽的温度传感器，在冶金、热工仪表领域得到广泛应用，是目前检测温度的主要传感器之一，尤其是在检测高温时更有优势，电厂也采用热电偶来测量温度。必须指出的是，热电偶的惰性在对象特性中占相当大的比例，所以必须予以考虑。假定热电偶的传递函数为

(15)

式中：τts为热电偶的时间常数。

根据文献[15]，一般假定现场τts约为30 s。因此，在换热器模型的实际工程应用时，应当考虑热电偶的惯性特性，如图4所示。

2.3 单相受热管集总参数模型的通道传递函数计算

单相受热管集总参数模型在控制工程应用时，需要导出受控通道和干扰通道的传递函数，以用于反馈控制器的设计或整定以及前馈控制器的设计或整定，这需要掌握推算各通道传递函数的方法。根据图4，可以归纳出各输入通道的传递函数计算公式。以喷水减温流量为例的单相受热管集总参数模型的各通道传递函数模型，如图5所示。具体的通道的传递函数计算公式和各通道的增益计算公式如下所述。

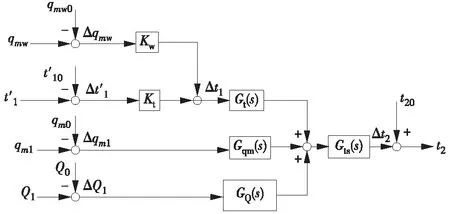
图4 考虑热电偶惯性的单相受热管集总参数模型Fig.4 Lumped parameter model of single-phase heat pipe considering thermocouple response

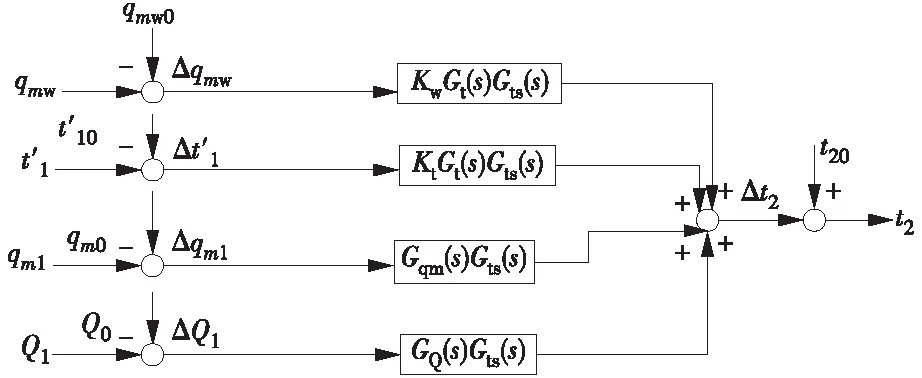
图5 单相受热管集总参数模型的通道传递函数模型Fig.5 Channel transfer function model of lumped parameter model of single-phase heat pipe

(1)入口汽温输入通道传递函数计算公式

(16)

(2)喷水流量输入通道传递函数计算公式

(17)

(3)蒸汽流量输入通道传递函数计算公式

(18)

(4)吸热量输入通道传递函数计算公式

(19)

3 单相受热管集总参数模型现代控制工程应用

3.1 集总参数模型方法仿真示例

根据文献[8]，以1 000 t/h直流锅炉过热器为例，其计算参数见表1。

根据表1所示的计算参数，就可以得到各通道的传递函数模型。

表1 1 000 t/h直流锅炉过热器计算参数Tab.1 Calculation parameters of 1 000 t/h DC boiler superheater

(1)对于入口汽温输入通道，根据式(7)、式(13)以及式(16)，可整理得到

(2)对于喷水流量输入通道，根据式(7)、式(12)以及式(17)，可整理得到

(3)对于蒸汽流量输入通道，根据式(8)以及式(18)，可整理得到

(4)对于吸热量输入通道，根据式(9)以及式(19)，可整理得到

3.2 集总参数模型现代控制工程应用评价

相较于分布参数模型，集总参数模型有如下几个优势。

(1)集总参数模型中的变量无需用相对量来表示，省去了将标幺量转换为实际量的过程，解决了放大增益始终为1的困扰。

(2)集总参数模型经计算得到的解就是线性化解，无需再简化；而分布参数模型经计算得到的解还需要进一步简化才能得到线性化解，可能会增大误差。

(3)集总参数模型是用出口这一点的介质参数来代表整个单相受热管的介质参数，所以忽略了沿管长方向的介质参数变化，故极大地简化了建模过程且使用过程也更加简便。

为了验证集总参数模型的可行性，现将集总参数模型与分布参数模型进行比较。通过计算，可得到同计算参数条件下的分布参数模型的传递函数。

(1)对于入口汽温输入通道

(2)对于喷水流量输入通道

(3)对于蒸汽流量输入通道

(4)对于吸热量输入通道

将集总参数模型与分布参数模型进行Matlab仿真试验比较。图6—9分别表示入口温度、喷水量、入口流量、热流量发生单位阶跃增加时出口温度的响应。

图6 入口温度阶跃增加时出口温度的响应Fig.6 Response of the outlet temperature to the inlet temperature step increase

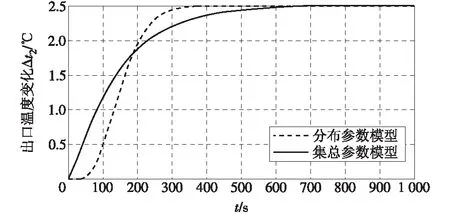
图7 喷水量阶跃增加时出口温度的响应Fig.7 Response of outlet temperature to the water spray volume step increase

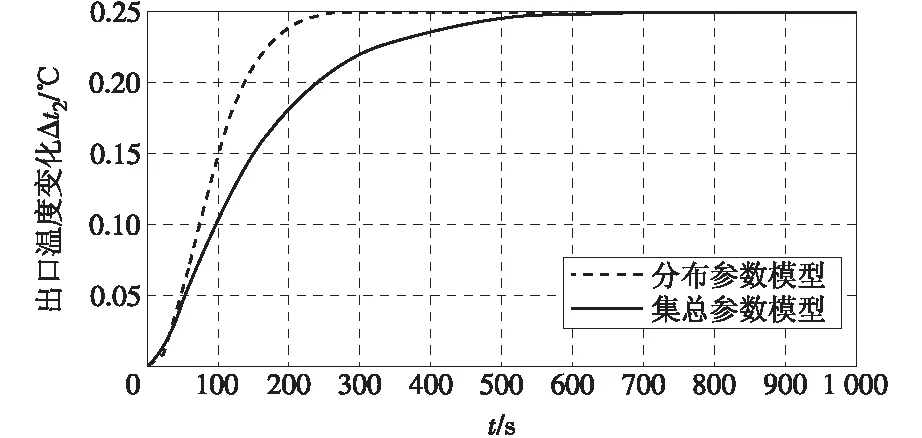
图8 入口流量阶跃减少时出口温度的响应Fig.8 Response of outlet temperature to the flow step decrease at inlet

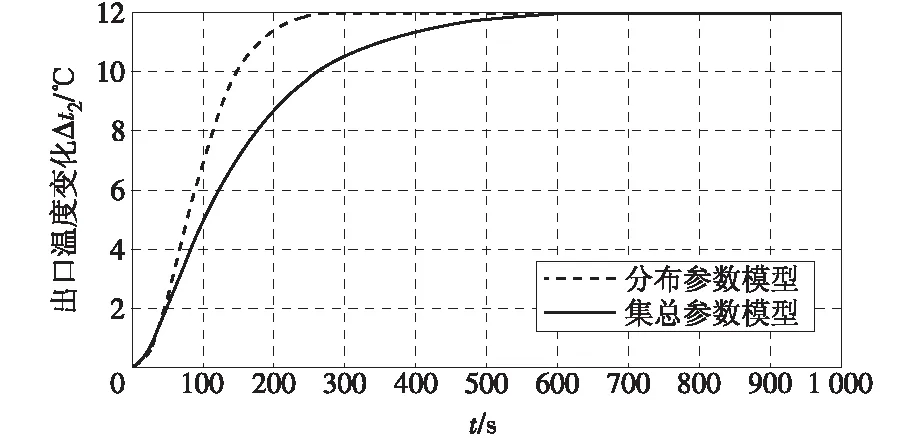
图9 热流量阶跃增加时出口温度的响应Fig.9 Response of outlet temperature to the heat flow step increase

从这4个动态响应图可以看出：集总参数模型能够较为真实地反映分布参数模型，且该模型更加简单，适用性更强，完全能满足现代控制工程应用的需要。因此，可以认为本课题建立的单相受热管集总参数模型可在现代控制工程中推广应用。同时，该模型还可为换热器类过程模型辨识工程中模型结构以及模型参数范围的确定提供一种有科学依据的可行方案。

4 结论

(1)本文建立了一套完整的符合现代控制工程应用的单相受热管的集总参数模型，实现了集总参数机理建模方法在现代控制工程中的应用。

(2)该模型解决了一些应用推广上的技术难题，如以喷水流量为例的过程控制量与模型输入量的转换方法等。

(3)该集总参数模型在控制工程中应用时，能达到与分布参数模型相似的控制效果；而对于建模过程，集总参数模型具有更明显的优势。

(4)本文所建立的单相受热管集总参数模型为换热器类过程模型辨识工程中模型结构以及模型参数范围的确定提供了一种有科学依据的可行方案。